GFC-空间中的GFS-KKM定理及其对极大元的应用
2016-05-06文开庭李和睿
文开庭, 李和睿
(贵州工程应用技术学院 土木建筑工程学院, 贵州 毕节 551700)
GFC-空间中的GFS-KKM定理及其对极大元的应用
文开庭,李和睿
(贵州工程应用技术学院 土木建筑工程学院, 贵州 毕节 551700)
摘要:引入GFC-空间中的GFS-KKM映射、G(KS)-映射和G(KS)-优化映射,建立GFC-空间的GFS-KKM定理,作为应用,获得G(KS)-映射和G(KS)-优化映射的极大元定理.结论统一、改进和推广一些近期文献的已知结果.
关键词:GFC-空间; GFS-KKM映射; G(KS)-映射; G(KS)-优化映射; 极大元
1预备知识
2009年,P. Q. Khanh等[1-2]引入了GFC-空间,2010年,P. Q. Khanh等[3]建立了GFC-空间中新的极大元定理、重合定理和相交定理.2011年,K. T. Wen等[4-5]得到了GFC-空间中新的相交定理、变分不等式、不动点定理和带上下界的广义平衡问题解的存在定理.文献[6]获得了GFC-空间中的KKM定理、Browder不动点定理等,文献[7-9]研究了GFC-空间中的匹配定理、不动点定理、极大极小不等式、鞍点定理、截口定理、重合定理、乘积GFC-空间中的极大元定理、广义混合拟平衡问题系统解的存在定理.文献[10-12]研究了H-度量空间和L-凸空间的KKM定理.文献[13-14]研究了FC-空间中的不动点.本文的目的是引入GFC-空间中的GFS-KKM映射、GKS-映射和GKS-优化映射;建立GFC-空间中GFS-KKM映射的GFS-KKM定理,作为应用,获得了GKS-映射和GKS-优化映射的极大元定理.我们的结论统一、改进和推广了一些近期文献的已知结果.
本文沿用文献[1-9]的相关记号、概念和术语,并引入如下概念.
定义 1.1设(X,Y,Φ)为GFC-空间,Z≠Ø,S:X→Z为单值映射.F:Y→2Z称为GFS-KKM映射,若对
有
定义 1.2设(X,Y,Φ)为GFC-空间,Z为拓扑空间,K为Z中的非空紧集,S:X→Z为单值映射.F:Z→2Y称为GKS-映射,若F有相对于K的弱紧局部交性质,且对
有
注 1.1定义1.2统一推广了文献[15-16]的W-映射、文献[17]的定义1、文献[18]的定义1.1.
定义 1.3设(X,Y,Φ)为GFC-空间,Z为拓扑空间,K为Z中的非空紧集,S:X→Z为单值映射.F:Z→2Y称为GKS-优化映射,若对∀z∈Z满足F(z)≠Ø,存在Fz:Z→2Y和z在Z中的开邻域N(z)使得:
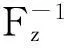
2) ∀t∈N(z),F(t)⊂Fz(t);
3) ∀N={y0,y1,…,yn}∈〈Y〉,∀{yi0,yi1,…,yik}∈〈N〉,

2主要结果

证明因F为GFS-KKM映射,故对
有
进而
设
首先,因F是紧闭值的,故对∀i∈{0,1,…,n},F(yi)是紧闭集,而S连续,故(S-1F)(yi)是紧闭集.又因φN(△n)紧,故对
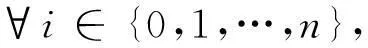
为闭集.据φN的连续性,对
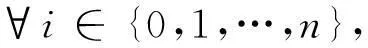
为闭集.
其次,因φN(△k)⊂φN(△n)且
故
于是

所以
进而
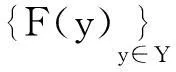
注 2.1定理2.1统一改进和推广了文献[24]的定理2.1、文献[25]的引理2.6、文献[26]的定理3.2、文献[27]的定理1、文献[28]的定理1.1、文献[29]的定理2.1,等.
定理 2.2设(X,Y,Φ)为GFC-空间,Z为拓扑空间,K为Z中的非空紧集,S∈C(X,Z),F:Z→2Y为GKS-映射.若存在M∈〈Y〉使得
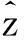
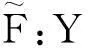

有
于是

即

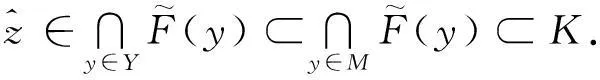
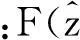


于是

注 2.2定理2.2统一改进和推广了文献[15]的定理1、文献[16]的定理1、文献[17]的定理1、文献[18]的定理2.1,等.

证明若结论不然,即
1) ∀z∈K,F(z)≠Ø.
因F为GKS-优化映射,故对∀z∈K,存在Fz:Z→2Y和z在Z中的开邻域N(z)使得
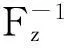
3) ∀t∈N(z),F(t)⊂Fz(t);
4) ∀N={y0,y1,…,yn}∈〈Y〉,∀{yi0,yi1,…,yik}∈〈N〉,
设F在K上的限制为FK:K→2Y定义为FK(z)=F(z),∀z∈K.对∀z∈K,设Fz在K上的限制为FzK:K→2Y定义为FzK(x)=Fz(x),∀x∈K.由于K紧,据2)得

6) ∀t∈N(z),FK(t)⊂FzK(t).
据K紧知
据4)得
7) ∀z∈K,∀N={y0,y1,…,yn}∈〈Y〉,∀{yi0,yi1,…,yik}∈〈N〉,
因Z是Hausdorff拓扑空间,K是Z中的紧子空间,故K是紧Hausdorff拓扑空间,因而,K是正规拓扑空间.故对∀z∈K和z在K中的开邻域N(z),存在z在K中的开邻域U(z)使得
据K的紧性知
8) 存在{z0,z1,…,zm}∈〈K〉使得
对∀p∈{0,1,…,m},定义Fp:K→2Y为:
则有



必有
若不然,假设存在
使得
任取
据8),存在p0∈{0,1,…,m}使得
注意到
故存在z*在K中的开邻域O(z*)使得
对
有
故
因此
于是
所以
与7)矛盾.
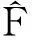
故

注2.3定理2.3统一改进和推广了文献[16]的定理2、文献[17]的定理2、文献[18]的定理2.2,等.
参考文献
[1] KHANH P Q, QUAN N H, YAO J C. Generalized KKM-type theorems in GFC-spaces and applications[J]. Nonlinear Anal,2009,71(3/4):1227-1234.
[2] HAI N X, KHANH P Q, QUAN N H. Some existence theorems in nonlinear analysis for mappings on GFC-spaces and applications[J]. Nonlinear Anal,2009,71(12):6170-6181.
[3] PHAN Q K, NGUYEN H Q. General existence theorems,alternative theorems and applications to minimax problems[J]. Nonlinear Anal,2010,72(5):2706-2715.
[4] WEN K T. A new intersection theorem in topological spaces with applications to variational inequalities and fixed points[C]//2nd International Conference on Artificial Intelligence. Management Science and Electronic Commerce,2011,2:923-926.
[5] WEN K T, LI H R. A new T-KKM theorem in GFC-spaces and its application to generalized equilibrium problems with lower and upper bounds[C]//2011 World Congress on Engineering and Technology,2011,1:543-546.
[6] 文开庭. GFC-空间中的KKM定理及其对一般拟平衡问题系统的应用[J]. 应用泛函分析学报,2012,14(3):292-297.
[7] WEN K T, LI H R. A matching theorem in GFC-spaces with application to saddle points[J]. Advanced Materials Research,2013,734-737(4):2867-2870.
[8] WEN K T. A new maximal theorem in product GFC-spaces with application to systems of generalized mixed vector quasiequilibrium problems[J]. Applied Mechanics and Materials,2013:405-408(4):3151-3154.
[9] 文开庭. GFC-空间中的Browder不动点定理及其对重合问题的应用[J]. 毕节学院学报,2013(4):26-32.
[10] 刘学文. H-度量空间中的一个新型KKM定理及其应用[J]. 四川师范大学学报(自然科学版),2003,26(2):154-157.
[11] 何蓉华,丁协平. L-凸空间的乘积空间内广义R-KKM型定理及其应用[J]. 四川师范大学学报(自然科学版),2004,27(1):27-30.
[12] 方敏,丁协平. L-凸空间内的广义L-R-KKM型定理及其应用[J]. 四川师范大学学报(自然科学版),2003,26(5) 461-463.
[13] 丁协平. 局部FC-空间内的Himmelberg型不动点定理[J]. 四川师范大学学报(自然科学版),2005,28(2):127-130.
[14] 丁协平. 局部FC-空间内Himmelberg型不动点定理的推广[J]. 四川师范大学学报(自然科学版),2006,29(1):1-6.
[15] ZHANG H L, WU X. A new existence theorem of maximal elements in non-compact H-spaces with applications to minimax inequalities and variational inequalities[J]. Acta Math Hungar,1998,80:115-127.
[16] WU X. New existence theorem for maximal elements in noncompact H-spaces with applications to equilibrium of games[J]. Comput Math Appl,2000,40:1097-1106.
[17] WEN K T. New maximal element theorems in L-convex spaces with application to equilibrium of games[J]. Math Appl China,2008,21(2):239-244.
[18] WEN K T. Maximal element theorems forWK-majorized mappings in FC-spaces and the application to equilibrium of abstract economies[J]. Adv Math China,2013,42(4):527-534.
[19] YANG M G, Deng L. Equilibria of nonparacompact generalized games withLcmajorized correspondences in FC-spaces[J]. Nonlinear Anal,2009,70(2):890-903.
[21] CHOWDHURY M S R, TARAFDAR E, TAN K K. Minimax inequalities on G-convex spaces with applications to generalized games[J]. Nonlinear Anal,2001,43(2):253-275.
[22] DING X P, XIA F Q. Equilibria of noncompact generalized games withLFCmajorized correspondences in G-convex spaces[J]. Nonlinear Anal,2004,56(6):831-849.
[23] SHEN Z F. Maximal element theorems of H-majorized correspondence and existence of equilibrium for abstract economies[J]. J Math Anal Appl,2001,256(1):67-79.
[24] DING X P. Generalized L-KKM type theorems in L-convex spaces with applications[J]. Comput Math Appl,2002,43(10/11):1249-1256.
[25] KIRK W A, SIMS B, YUAN X Z. The Knaster-Kuratowski and Mazurkiewicz theory in hyperconvex metric spaces and some of its applications[J]. Nonlinear Anal,2000,39(5):611-627.
[26] DING X P. Generalized G-KKM theorems in generalized convex spaces and their application[J]. J Math Anal Appl,2002,266(1):21-37.
[27] PARK S. Fixed point theorems in locally G-convex spaces[J]. Nonlinear Anal:TMA,2002,48(6):869-879.
[28] CHOWDHURY M S R, TARAFDER E, TAN K K. Minimax inequalities on G-convex spaces with applications to generalized game[J]. Nonlinear Anal,2001,43(2):253-275.
[29] WEN K T. New GRKKM theorems in FC-spaces with application to fixed points[J]. Adv Math China,2010,39(3):331-337.
2010 MSC:47H04; 47H10; 52A99
(编辑李德华)
A GFS-KKM Theorem in GFC-Spaces with the Application to Maximal Elements
WEN Kaiting,LI Herui
(SchoolofCivilEngineeringandArchitecture,GuizhouUniversityofEngineeringScience,Bijie551700,Guizhou)
Abstract:In this paper, GFS-KKM mappings, G(KS)-mappings and G(KS)-majorized mappings are introduced, a GFS-KKM theorem is established in GFC-spaces. As applications, maximal element theorems for G(KS)-mappings and G(KS)-majorized mappings are obtained. Our results unify, improve and generalize some known results in recent references.
Key words:GFC-space; GFS-KKM mapping; G(KS)-mapping; G(KS)-majorized mapping; maximal element
doi:10.3969/j.issn.1001-8395.2016.01.016
中图分类号:O177.91
文献标志码:A
文章编号:1001-8395(2016)01-0093-05
作者简介:文开庭(1962—),男,教授,主要从事非线性分析的研究,E-mail:wenkaiting_2004@sina.com
基金项目:国家自然科学基金(11361003)、贵州省自然科学基金([2011]2093)和贵州省教育厅自然科学重点基金([2012]058)
收稿日期:2014-05-05
