模的fann-内射维数及fann-平坦维数

徐龙玉,　万吉湘,　乔　磊

(　　　1. 西南科技大学 理学院, 四川 绵阳 621010;　2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621000;

3. 四川师范大学 数学与软件科学学院, 四川 成都 610066)



模的fann-内射维数及fann-平坦维数

徐龙玉1,万吉湘2,乔磊3

(1. 西南科技大学 理学院, 四川 绵阳 621010;2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621000;

3. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

摘要：设R为环,给出R-模的fann-内射维数、fann-平坦维数概念,并在此基础上定义R的左整体fann-维数(记为I.fa.ID(R))和R的右整体fann-平坦维数(记为r.fa.FD(R)).若记所有fann-内射R-模构成的类为FAI,证明了若FAI满足单同态的上核是封闭的,则有I.fa.ID(R)=r.fa.FD(R),且此时I.fa.ID(R)≤1的充要条件是R的每个有限生成左零化子都是投射模.

关键词：fann-内射模; fann-内射维数; fann-平坦模; fann-平坦维数; 左AC环

1预备知识

fann-内射模和fann-平坦模的概念最初见诸于文献[1].对R的子集X,令

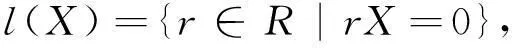
则l(X)称为R的左零化子.注意有l(X)=l(I),其中I是由X生成的右理想.回顾右R-模N称为fann-平坦模[1],是指对R的任意有限生成的左零化子l(I),自然同态N⊗Rl(I)→N⊗RR是单同态,亦即0→N⊗Rl(I)→N⊗RR是正合列.回顾左R-模M称为fann-内射模[1],是指对环R的任意有限生成左零化子l(I),R-模同态f:l(I)→M都能扩张成同态g:R→M,即有交换图1.

称环R为左AC环,是指R的任意有限生成的左零化子理想l(I)都是有限表现的[1].显然内射模是fann-内射模,平坦模是fann-平坦模.当R是整环时,任何模都是fann-内射模,也都是fann-平坦模.

(同调)维数一直是同调代数中研究的焦点.自然地,对任何由推广内射模和推广平坦模而得到的新的模类[2-12],人们总是希望定义新的维数来刻画环的性质[13-17],其中,L. X. Mao等[13]给出了FP-投射维数的定义,并用此维数研究了Noether环和Coherent环,也得到了FP-内射维数与其他维数之间的关系.相应地,我们也利用fann-内射模和fann-平坦模定义模的fann-内射维数与模的fann-平坦维数,以及环的左整体fann-内射维数l.fa.ID(R)和右整体fann-平坦维数r.fa.FD(R).通过对这些维数的系统讨论,给出AC环的许多性质刻画.

本文中所有的环都是带有单位元1的结合环,所有的模都是酉模.

2fann-内射维数及fann-平坦维数

定义 2.11) 设M是左R-模,M的左fann-内射维数是指使得Extn+1(R/l(I),M)=0的最小非负整数n,记为l.fa-id(M)=n,其中l(I)取遍环R所有有限生成的左零化子理想.如果这样的n不存在,则称M的左fann-内射维数为∞,记为l.fa-id(M)=∞.

2) 定义

l.fa.ID(R)=sup{l.fa-id(M)|M∈RM},

称之为环R的左整体fann-内射维数.

定义 2.21) 设N是右R-模.N的右fann-平坦维数是指使得Torn+1(N,R/l(I))=0的最小非负整数n,记为r.fa-fdRN=n,其中l(I)取遍环R所有有限生成的左零化子理想.如果这样的n不存在,则称N的右fann-平坦维数为∞,记为r.fa-fd(N)=∞.

2) 定义

r.fa.FD(R)=sup{r.fa-fd(N)|N∈MR},

称之为环R的右整体fann-平坦维数.

例 2.3自然地,左R-模M是fann-内射模当且仅当l.fa-id(M)=0.同理,右R-模N是fann-平坦模当且仅当r.fa-fd(N)=0.对任何右(或左)R-模N,记N+=HomZ(N,Q/Z),称之为N的特征模.

命题 2.4右R-模N是fann-平坦右R-模当且仅当N+是fann-内射左R-模.

证明对R的任意有限生成的左零化子理想l(I),由自然同构

知结论成立.

命题 2.5设{Mi}是一簇左R-模,则⊕Mi是fann-内射模当且仅当每一Mi是fann-内射模.

证明对环R的任意有限生成的左零化子理想l(I),由自然同构

知结论成立.

下面把fann-内射左R-模类和fann-平坦右R-模类分别记为FAI和FAF.

命题 2.6模类FAF在纯子模下封闭.

证明设A是fann-平坦右R-模B的纯子模.由文献[18],0→(B/A)+→B+→A+→0是分裂的正合列.由命题2.4,B+是fann-内射左R-模,因此有A+是fann-内射左R-模.仍由命题2.4,A是fann-平坦模.

定理 2.7对环R,以下条件等价:

1) 环R是左AC环;

2) fann-平坦右R-模的直积是fann-平坦模;

3) 左R-模M是fann-内射模当且仅当M+是fann-平坦右R-模.

定理 2.8对环R,以下等价:

1) l.fa.ID(R)=0;

2) r.fa.FD(R)=0;

3) 每个左R-模是fann-内射模;

4) 每个右R-模是fann-平坦模;

5) 每个有限生成的左零化子理想l(I)是R的纯子模.

定理 2.9对环R,以下条件等价:

1) FAI中单同态的上核是封闭的;

2)R是左AC环,且FAF中满同态的核是封闭;

3)R是左AC环,且有Tork(N,R/l(I))=0,其中k≥1,N是fann-平坦右R-模,l(I)是R的有限生成左零化子;

4) Extk(R/l(I),M)=0,其中k≥1,M是fann-内射左R-模,l(I)是R的有限生成的左零化子.

其次令0→A→B→L→0是右R-模正合列,其中B及L是fann-平坦右R-模,则有正合列0→L+→B+→A+→0,又因为B+及L+是fann-内射左R-模,故A+是fann-内射左R-模,则A是fann-平坦右R-模.

为陈述简洁起见,我们用(X)表示性质:模类FAI满足单同态的上核是封闭的.

显然无零因子环有性质(X).

定理 2.10设环R有性质(X),则对左R-模M,以下条件等价:

1) l.fa-id(M)≤n;

2) 设0→M→E0→E1→…→En-1→Ln→0是正合列,其中E0,E1,…,En-1是fann-内射模,则Ln是fann-内射R-模;

3) 对R的每个有限生成的左零化子l(I),有Extn+1(R/l(I),M)=0;

4) 对R的每个有限生成的左零化子l(I),及k≥1,有Extn+k(R/l(I),M)=0.

对偶地,可以证明下面的定理.

定理 2.11设环R有性质(X),则对右R-模N,以下条件等价:

1) r.fa-fd(N)≤n;

2) 设0→Kn→Fn-1→…→F1→F0→N→0是正合列,其中F0,F1,…,Fn-1是fann-平坦右R-模,则Kn是fann-平坦右R-模;

3) 对R的每个有限生成的左零化子l(I),有Torn+1(N,R/l(I))=0;

4) 对R的每个有限生成的左零化子l(I),及任何k≥1,有Torn+k(N,R/l(I))=0.

定理 2.12设环R有性质(X),n是非负整数,则l.fa.ID(R)≤n当且仅当r.fa.FD(R)≤n.

推论 2.13设环R有性质(X),则l.fa.ID(R)=r.fa.FD(R).

定理 2.14设R有性质(X),且l.fa.ID(R)<∞,则l.fa.ID(R)=r.fa.FD(R)=l.fa-id(RR).

证明只需证l.fa.ID(R)≤l.fa-id(RR).设m=l.fa-id(RR)<∞,则有正合列0→R→E0→E1→…→Em-1→Em→0,其中E0,E1,…,Em-1,Em是fann-内射模.于是有正合列0→⊕R→⊕E0→⊕E1→…→⊕Em-1→⊕Em→0,于是对任意自由左R-模F有l.fa-id(F)≤m.

记n=l.fa.ID(R)<∞.设M是左R-模,取正合列0→Kn→Fn-1→…→F1→F0→M→0,其中F0,F1,…,Fn-1是自由模.由于l.fa-id(Kn)≤n,及l.fa-id(Fi)≤m,则对R的有限生成的左零化子l(I),有Extm+1(R/l(I),M)≅Extm+n+1(R/l(I),Kn)=0,故l.fa-id(M)≤m,因此有n≤m.

定理 2.15对环R,以下条件等价:

1)R的有限生成的左零化子l(I)是投射模;

2)R是左AC环,且fann-平坦右R-模的子模是fann-平坦模;

3)R是左AC环,且R的右理想是fann-平坦模;

4) fann-内射左R-模的商模是fann-内射模;

当R有性质(X)时,上面各条又等价于:

5) l.fa.ID(R)≤1;

6) r.fa.FD(R)≤1.

参考文献

[1] 徐龙玉,汪明义. 关于零化子凝聚环[J]. 四川师范大学学报(自然科学版),2006,29(2):161-165.

[2] 王芳贵,汪明义,杨立英. 交换环上的极大性内射模[J]. 四川师范大学学报(自然科学版),2010,33(1):1-9.

[3] 章聚乐,陈建龙.P-内射环和半素环[J]. 数学杂志,1991,11(1):29-34.

[4] 赵玉娥,杜先能. 关于广义内射模的一些研究[J]. 四川师范大学学报(自然科学版),2008,31(5):16-18.

[5] 易忠. 关于quasi-投射模和quasi-内射模[J]. 广西师范大学学报(自然科学版),1985,3(1):18-26.

[6] 余柏林. π-凝聚环的推广[J]. 四川师范大学学报(自然科学版),2005,28(3):278-281.

[7] 李珊珊,汪明义. 关于p-平坦模[J]. 广西师范大学学报(自然科学版),2004,22(1):36-40.

[8] GUPTA R N. Onf-injective modules and semihereditary rings[J]. Proc Nat Inst Sci,1969,35(1):323-328.

[9] JAIN S. Flat and FP-injectivity[J]. Proc Am Math Soc,1973,41(2):437-442.

[10] 徐龙玉,宋晖. 关于fann-内射模[J]. 四川师范大学学报(自然科学版),2009,32(4):443-446.

[11] 陈文静,杨晓燕. 弱Gorenstein FP-内射模[J]. 四川师范大学学报(自然科学版),2014,37(4):477-481.

[12] 尹华玉,陈幼华. π-整环上形式幂级数的容度准则[J]. 四川师范大学学报(自然科学版),2014,37(4):451-454.

[13] MAO L X, DING N Q. FP-projective dimensions[J]. Commun Algebra,2005,33:1153-1170.

[14] STENSTROM B. Coherent rings and FP-injective modules[J]. J London Math Soc,1972,2:372-383.

[15] NG H K. Finitely presented dimension of communicative rings and modules[J]. Pacific J Math,1984,113(2):25-40.

[16] 汪明义. 代数学中Frobenius的结构[M]. 北京:科学出版社,2005:78-96.

[17] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006:142-193.

[18] ENOCHS E. A note on absolutely pure modules[J]. Canad Math Bull,1976,19(3):361-362.

2010 MSC：13C10; 13C11; 13D07

(编辑郑月蓉)

On Fann-Injective Dimension and Fann-Flat Dimension

XU Longyu1,WAN Jixiang2,QIAO Lei3

(1.CollegeofScience,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan;2.CollegeofMathematicsandComputerScience,MianyangNormalCollege,Mianyang621010,Sichuan;3.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Abstract：In this paper, for a ring R the notions of fann-injective dimension and fann-flat dimesion are introduced. Based on these, the left global fann dimension of R, denoted by I.fa.ID(R) and the right global fann dimension of, denoted by r.fa.FD(R) are defined. Moreover, let (X) express the codition that the uppe kernelsof injective homomorphisms are closed and denote the class of all fann-injective R-modules as FAI. It is proved that if FAI satisfies (X) then I.fa.ID(R)=r.fa.FD(R) and in this case, I.fa.ID(R)≤1 if and only if every finitely generated left annihilator in R is projective.

Key words：fann-injective modules; fann-injective dimension; fann-flat modules; fann-flat dimension; left AC ring

doi:10.3969/j.issn.1001-8395.2016.01.006

中图分类号：O153; O154

文献标志码：A

文章编号：1001-8395(2016)01-0033-04

作者简介：徐龙玉(1979—),女,讲师,主要从事环与模范畴理论的研究,E-mail:xulongyu3@163.com

基金项目：国家自然科学基金(11171240)

收稿日期:2014-07-08