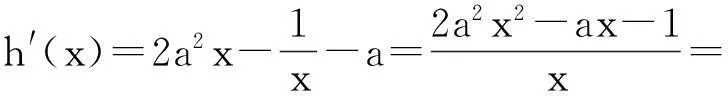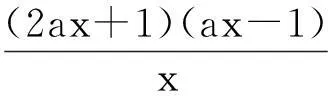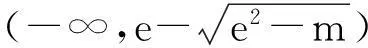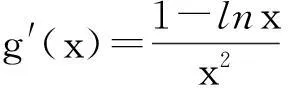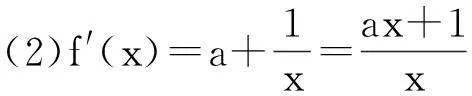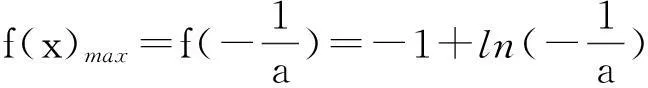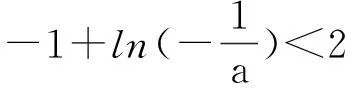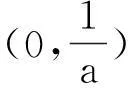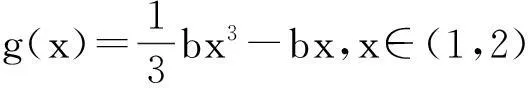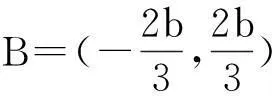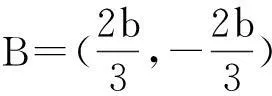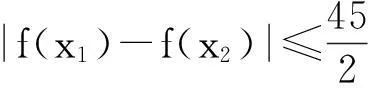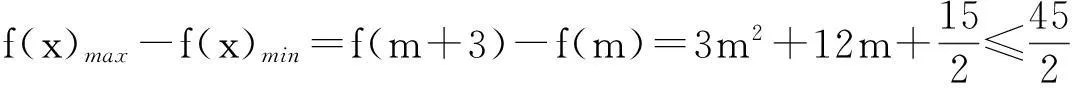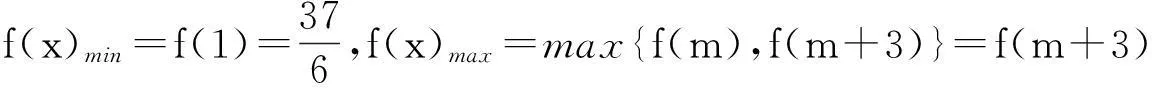例析函数中的恒成立问题与存在性问题



例析函数中的恒成立问题与存在性问题

江西省赣州中学(341000)李金花

谈及高中数学最重要的知识内容，无疑是函数，作为高中数学的核心内容，函数与导数的综合是高考的热点，多以压轴题出现，难度较大，区分度较强，可见其在高中数学中的地位极其重要！而“恒成立”或“存在性”问题始终占据着函数最难最重要的位置，这些问题中，导数都是函数研究的重要工具，而将问题的思想方法准确地分析出来，这是问题的难点.笔者作为高中一线教师，通过对各省市试题及多种教辅资料分析，总结出了几种非常常见，数学思想极其丰富的几大题型，给广大师生参考.

1变量相同，函数不同的恒成立与存在性问题

(1)对任意x∈[a,b]都有f(x)

(2)存在x0∈[a,b]使得f(x0)

(3)存在x0∈[a,b]使得f(x0)=g(x0)成立

解题思路：这类问题三大题型的解题思路基本一致，函数f(x)与g(x)中的变量是一样的，故这两个函数是同时变化的.其解题思路是首先考虑分离其中的参数，分离成m

例1设f(x)=ax+2,g(x)=a2x2-lnx+2,a∈R.

(1)若a=2，求曲线y=g(x)在点(1,g(1))处的切线方程；

(2)是否存在负数a，使f(x)≤g(x)对一切正数x都成立？若存在，求a的取值范围；若不存在，请说明理由.

解：(1)易得7x-y-1=0.

(2)令h(x)=g(x)-f(x)=a2x2-lnx-ax，则原题等价于h(x)min≥0,x∈(0,+∞).

2变量不同，函数不同的恒成立与存在性问题

(1)对任意x1∈[a,b]，任意x2∈[c,d]，都有f(x1)

解题思路：这类问题显然与第一类问题不同，其函数f(x)与g(x)中的变量是不同的，变量之间没有关联，故这两个函数是各自变化的.题意要求y=f(x),x∈[a,b]中的任意一个函数值均小于y=g(x),x∈[c,d]中的任意一个函数值，故问题可转化为f(x)max(x∈[a,b])

(1)讨论函数f(x)的单调区间；

(2)若对任意x1,x2∈(0,+∞),g(x1)

(2)对任意x1∈[a,b]，均存在x2∈[c,d]，使得f(x1)

解题思路:该题型与题型二相似，题意要求y=f(x),x∈[a,b]中的任意一个函数值均小于y=g(x),x∈[c,d]中的某一个函数值，故问题可转化为f(x)max(x∈[a,b])

例3已知函数f(x)=ax+lnx.

(1)若a=2，求曲线y=f(x)在x=1处的切线的斜率；

(2)讨论f(x)的单调区间；

(3)设g(x)=x2-2x+2，若对任意x1∈(0,+∞)，均存在x2∈[0,1]，使得f(x1)

解：(1)易得k=3.

3变量不同，函数相同的恒成立与存在性问题

(1)对任意x1∈[a,b]，均存在x2∈[c,d]，使得f(x1)=g(x2)成立

解题思路：对于这类题型，题意是要求对于y=f(x),x∈[a,b]中的任意一个函数值，都在y=g(x),x∈[c,d]的函数值中.故原题可转化为y=f(x),x∈[a,b]的值域A⊆y=g(x),x∈[c,d]的值域B.

例4已知f(x)=lnx-ax(a∈R).

(1)讨论f(x)的单调区间；

(2)设y=f(x),x∈(1,2)的值域为A，y=g(x),x∈(1,2)的值域为B，由题意可知，A⊆B.

(2)对任意x1,x2∈[a,b]，|f(x1)-f(x2)|≤ξ(ξ>0)恒成立

解题思路：对于这类题型，题意是在y=f(x),x∈[a,b]中，任取两个函数值，这两个值之差不超过ξ，故原题可转化为f(x)max-f(x)min≤ξ,x∈[a,b]，只需求出y=f(x),x∈[a,b]的最大值和最小值即可解决.

(1)求f(x)的解析式；

综上，m的取值范围为0≤m≤1.

以上几道例题是函数“恒成立”和“存在性”问题中的常见题型，题目融合了很多知识点和数学思想方法，分离参数构造函数和作差构造函数都是解决这类问题的通法，结合了分类讨论、转化与化归、数形结合等思想方法，导数是解决与函数有关问题的强有力的工具.我们在教学中要选择典型题目并进行深层次的理解或延伸，把握好解题思路，将问题的条件和结论自然融合.当然，教学中要有针对性地进行综合训练，高考复习才能高效，学生才能有所进步.