一类分式最值的常规解法
2016-05-05刘宜兵,郑修凤
中学数学研究(江西) 2016年3期
一类分式最值的常规解法
湖北省宜都市一中(443300)刘宜兵郑修凤
有这样一道数学竞赛试题:
本题在文[1],[2],[3]都给出了不少的巧妙解法.但无论是巧证还是简证,技巧性都比较强,一般的学生都不易掌握.本文给出一个易为普通学生能掌握的方法,因为在解题过程中两次用到判别式法,故称之为“双判别式法”.



以y为主元整理得


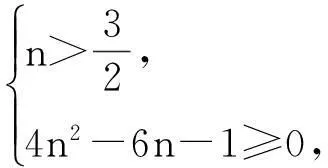

说明:这类题目在许多考试中都是求代数式的最大或最小值(即事先不知道最值).所以上述方法较文[1],[2],[3]中给出的证明方法要好,且求解过程中仅仅只用到了恒成立的相关知识,大多数学生是能掌握的.
下面再看一道题.
例2若实数a,b,c满足a2+b2+c2=1,求3ab-3bc+2c2的最大值.





下面探讨等号成立的条件.

下面一道习题也是数学竞赛试题:
参考文献
[1]张赟.两个“怪异”不等式的统一简证[J].中学数学教学参考,2012(7)(上旬刊).
[2]邹生书.巧“设”妙“分”求最值[J].数学通讯,2011(3) (下半月).
[3]秦庆雄,范花妹.拉格朗日方法解题例说[J].数学通讯,2014(2) (下半月).
