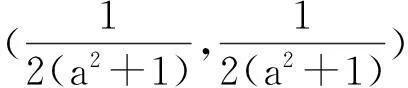利用对称性巧解函数稳定点问题



利用对称性巧解函数稳定点问题

浙江省绍兴市鲁迅中学(312000)陈少春虞关寿

近日在学校的一次教研活动中，笔者抛出了两个关于函数不动点和稳定点的问题：

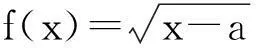
(2)若x0满足f(f(x0))=x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点.如果f(x)有两个二阶周期点x1，x2，试确定a的取值范围.

对于第一个问题的解答，很多老师都会采用函数不动点和稳定点的一个性质：

对于第二个问题，参考答案所给出的方法是通过分类讨论思想来求解，思考方式自然但过程冗长和繁琐，学生若按这样去思考与解答是很容易出错的.为此我们就要考虑有没有比较简便的方法来解决这个问题？笔者认为要解决这个问题关键是找到不动点和稳定点的本质关系，为此笔者想对两者之间的关系作一些探究，跟各位同行交流.

上面给出的函数不动点和稳定点的性质其实已经给出了两者之间的一个关系，但笔者认为条件太强了，它要求这个函数是单调递增的才能得到不动点集合A等于稳定点集合B.但是如果一个函数不单调，就没法用这个性质解决，笔者在一些报刊杂志上看到过讨论研究不动点和稳定点问题的文章，它们经常会引用一个例子：“已知二次函数f(x)=ax2-1(x∈R)，且f(x)的不动点集合A、稳定点集合B满足A=B≠∅，求实数a的取值范围.”作为问题讨论的依据.

下面笔者给出函数不动点和稳定点关系另一个常用的性质：

设f(x)是连续函数，其不动点集合为A={x|f(x)=x}，稳定点集合为B={x|f(f(x))=x}，则A=B当且仅当函数f(x)的图像上不存在关于直线y=x(落在直线y=x上的点除外)对称的点.

在证明这个性质前我们先来研究一下稳定点具有怎样的几何性质，我们都知道不动点都是稳定点，那么除了不动点之外还有没有别的点也是稳定点呢？我们不妨设x0是函数y=f(x)的一个稳定点(x0≠f(x0))，即f(f(x0))=x0，令t=f(x0)，则x0=f(t).由上可得(x0,t)，(t,x0)是函数y=f(x)图像上的点且f(f(t))=t，即t也是一个稳定点，从而得到不是不动点的稳定点的个数一定是偶数且这些稳定点是两两关于直线y=x对称的，所以稳定点集合由不动点和函数图像上关于直线y=x对称的点的横坐标构成.接下来我们证明上面给出的性质.

证明：(充分性)当A=B时，即稳定点都是不动点(落在直线y=x上的点的横坐标)，故函数f(x)的图像上不存在关于直线y=x(落在直线y=x上的点除外)对称的点.

(必要性)反证法，假设A≠B，则存在x0满足f(f(x0))=x0，令t=f(x0)且t≠x0，则x0=f(t).即(x0,t)，(t,x0)都是函数y=f(x)上的点，与函数f(x)的图像上不存在关于直线y=x(落在直线y=x上的点除外)对称的点矛盾.命题得证.

研究清楚了不动点和稳定点的关系后，下面例举几题体会该性质给问题解决带来的方便.

(2)若x0满足f(f(x0))=x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点.如果f(x)有两个二阶周期点x1，x2，试确定a的取值范围.

解：(1)略.

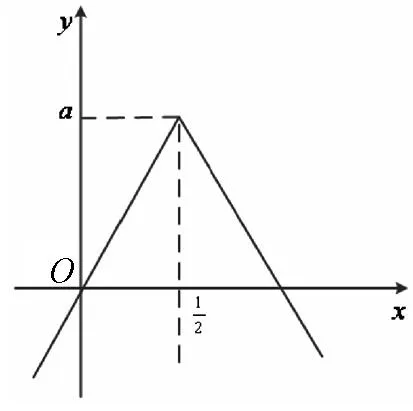
图1

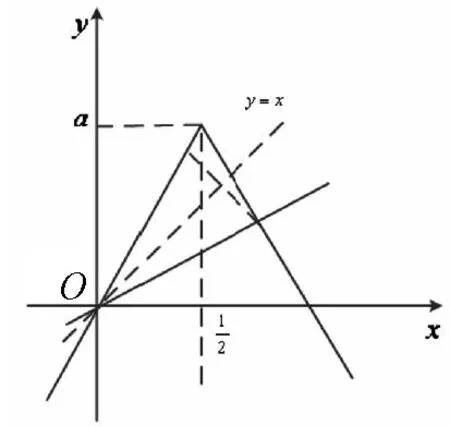
图2

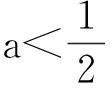
根据上面的解题过程，我们可以对该题作进一步的推广：

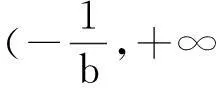
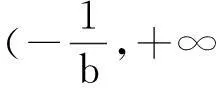
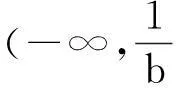
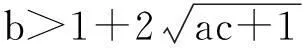
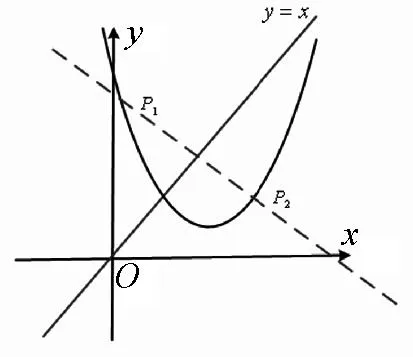
图3

证明：由

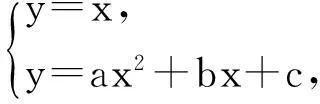
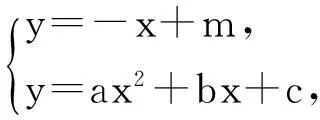
例3已知实数集为R，f(x)=ax2+bx+c(a,b∈R)且A={x|x=f(x),x∈R}，B={x|x=f(f(x)),x∈R}，那么

(1)当a=1，且A={-1,3}时，B=；

(2)A与B的关系为；

(3)当b=0,c=-1,且A=B≠∅时，求实数a的取值范围.

解：(1)f(x)=x2+bx+c，-1,3是方程f(x)=x的两个不同实数根，则由韦达定理知-1+3=1-b，-1·3=c，∴b=-1，c=-3.

(2)A⊆B；

(3)f(x)=ax2-1，若a=0不符合题意；

例4已知函数y=f(x)，若存在x0，使得f(x0)=x0，则称x0是函数y=f(x)的一个不动点，若x0满足f(f(x0))=x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点.设二次函数f(x)=ax2+(b+1)x+b-2.

(1)当a=2,b=1时，求函数f(x)的不动点；

(2)若对于任意实数b，函数f(x)恒有两个不同的不动点，求实数a的取值范围；

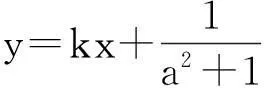
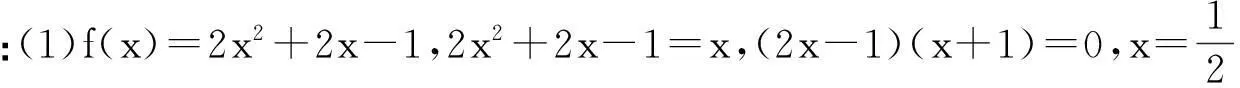
(2)对任意实数b，方程ax2+(b+1)x+b-2=x恒有两个不同的根，即ax2+bx+b-2=0恒有两个不同的根.∴Δ=b2-4a(b-2)=b2-4ab+8a>0对任意实数b恒成立，Δ1=16a2-32a<0，

∴0

参考文献

[1]彭佳麒.函数的不动点和稳定点[J].数学教学，2011(7)：37.

[2]2013全国及各省市高考试题全解.