平面内凸四边形的一组重要性质



平面内凸四边形的一组重要性质

内蒙古师范大学附属中学(010020)王洪军

《数学通讯》2014年第5期刊登了程汉波老师的文章《四边形中位线的性质及其应用》，笔者阅读后深受启发，经过仔细推敲，得出平面内凸四边形的一组重要性质，现整理成文，与读者分享.

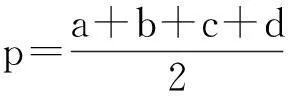
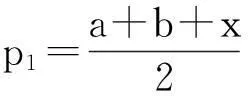
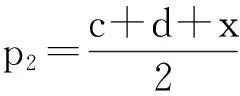
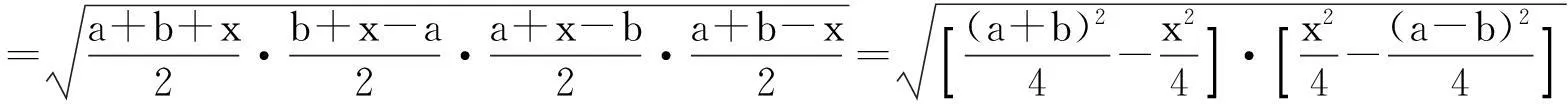
同理，在ΔACD中，我们也能得到

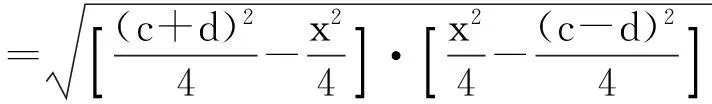
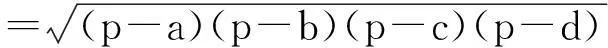
当且仅当[(a+b)2-x2]·[(c+d)2-x2]=[x2-(a-b)2]·[x2-(c-d)2]时，等号成立.借助余弦定理可将上式化为(1+cosB)(1+cosD)=(1-cosB)(1-cosD)，整理可得cosB+cosD=0，则B+D=π，因此，当且仅当四边形ABCD内接于圆时，面积取得最大值.

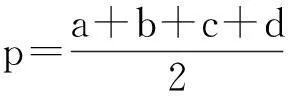
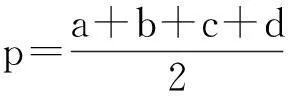
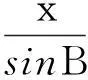
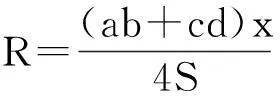
在ΔABC和ΔACD中，分别用余弦定理可得

x2=a2+b2-2abcosB①，x2=c2+d2-2cdcosD②,①×cd+②×ab，并整理，可得

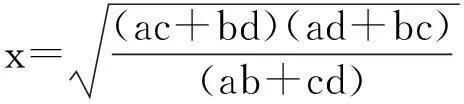
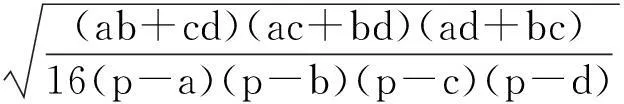
参考文献

[1]程汉波.四边形中位线的性质及其应用[J].数学通讯(下半月)，2014(5).