带有暗流的赤道水波的稳定性

兰天柱,陈晓和,徐衍聪

(杭州师范大学理学院, 浙江 杭州, 310036)

带有暗流的赤道水波的稳定性

兰天柱,陈晓和,徐衍聪

(杭州师范大学理学院, 浙江 杭州, 310036)

通过使用短波扰动的方法, 在拉格朗日坐标中研究了 f 平面上带有暗流的赤道水波的稳定性. 通过证明得到如下结论: 如果忽略地球的转速, 则赤道水波的不稳定区域将不受暗流影响, 同时得到了具有某一流速的水流的不稳定区域.

拉格朗日坐标;局部不稳定性;短波的方法;赤道水波

1 介绍

在过去的几十年里,人们对赤道附近的海洋变化进行广泛的研究和讨论,特别是存在于海洋和大气中的流和暗流之间的相互作用,所有的这些都成为解释厄尔尼诺现象的关键性因素.与此同时,人们在拉格朗日坐标中,得到了非线性赤道流的一些精确解,例如:[1]中得到了拉格朗日坐标下的同质周期解,这些解在Gerstners波的模型[2-5]中被重新发现,进而被用于描述许多有趣的重力边缘波.[6]得到了一个上面是温跃层,下面是近地表,向西传播的地球内部物理波的非线性解.这个出现在拉格朗日坐标下的解被用来描述每个粒子的循环路径.在一截狭窄的、关于赤道对称的赤道带内部赤道波是存在的.与[7-8]中所提到的平面情况相比,本文中我们研究向西传播的海洋波.实际上,有了精确解后,解的稳定性问题,即随着时间的变化,是否存在对解的扰动变得尤为重要.在古典的谱方法和能量法之外,短波法(类似于光线理论中得到的几何光学方法)在三维非粘性不可压缩流体动力稳定/不稳定理论中扮演着重要的角色.这个方法在[9-13]中用来分析波包的扰动对波的变化影响.常微分方程组系统描述了沿着流动轨迹的波包动力学行为.在几何光学的语言中,这个常微分方程系统包含着用来描述波速的程函方程(Eikonal equation)以及描述速度振幅的运输方程.速度振幅的渐近行为具有稳定性.流不稳定的一个充分条件是没有一个轨迹伴随着摄动速度的幅度而变化.在第三部分,我们将介绍短波不稳定方法.短波法已经被应用到一系列的稳定性问题当中,例如:[14]中的Kirchoff-Kida漩涡稳定性,[15]中的涡环与漩涡、涡环与无漩涡的稳定性.在拉格朗日坐标中,短波法被成功应用到描述基本波.例如:[16]中的Gerstners波,[7,17]中的赤道陷波.第四部分,在拉格朗日坐标中,我们利用短波法研究了f平面上带有暗流的赤道水波的稳定性.

2 预备知识

地球被认为是一个绕极轴朝东旋转、半径(R=6371km),转速Ω=7.29×10-5转/s的球体.在一个旋转坐标系上,其中原点是地球表面的一个点,建立笛卡尔坐标,(x,y,z)分别代表经度、纬度和垂直线.[18]中提出的物理海洋波的欧拉控制方程如下:

(1)

满足质量守恒：

ρt+uρx+uρy+wρz=0.

(2)

不可压缩性条件：

ux+vy+wz=0,

(3)

这里，t,α分别代表、时间和纬度，g=9.81m/s2是地球表面重力加速度,ρ是水的密度，P是压强,在[19]中提到的f平面近似代替的欧拉方程如下：

(4)

[6]中,通过假设在时间t时的位置,得到了上述方程的如下行波解:

(5)

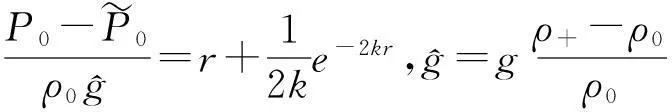
(6)

ρ+是所在区域水的密度.由上面可知P0决定了唯一的r+>r0,这里r+>0是如下方程唯一的解:

(7)

在水流所在区域取如下合适的压强梯度:

(8)

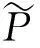
(9)

注意到当c<0时，中间项ω始终是负数，第一项和第三项为零.

我们注意到式(5)右端的雅克比矩阵如下:

(10)

矩阵所在行列式的值为1-e-2ξ,在这里

ξ=kr,θ=k(q-ct),

(11)

F的逆矩阵为:

(12)

3 短波不稳定法

令U(t,x)是非粘性不可压缩流的速度场.U称为基本流.假设这个速度场受到一个速度场u(t,x)的小扰动.把U+u带入到欧拉方程组和后面的方程.并且忽略边值条件以及u的平方项.最终的方程组控制着扰动速度场的动力学行为.这就是所谓的线性欧拉方程:

ut+(U+u)·▽u+(u·▽)U+Qu=-▽p,

(13)

(14)

这里,p(t,x)是P(t,x)的一个小扰动.我们可以利用短波不稳定法,考虑迅速变化的局部波包(这种技术被称为Wentzel-Kramers-Brillouin(WKB)-近似,首先被应用在量子力学).假设这个小扰动有如下的形式:

(15)

(16)

这里ε是渐近分析中使用的一个小参数,A是一个向量函数,同时Φ和B是标量函数.

若式(15)-(16)解决线性化欧拉方程(13)-(14),并且带有[11]中提到的初值条件,如下:

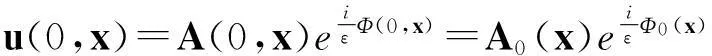
(17)

这时,由ε的最高次项可知,波相Φ(t,x)满足程函方程(Eikonal equation)

Φt+U·▽Φ=0,

(18)

同时,波幅A(t,x)满足如下方程:

At+(U·▽)A+(A·▽)U+QA=-iB(t,x)▽Φ.

(19)

实际上,将式(15)带入(14),同时令ε1和ε0的系数为零,我们可以得到如下结果:

▽·A=0,

(20)

以及

A·▽Φ=0.

(21)

因此,在初始时间,波幅A0和波速▽Φ0一定是正交的,即

A0·▽Φ0=0.

(22)

由式(15)和(21)可得:

u·▽Φ=0.

(23)

将式(15)(16)代入(13),令含有ε1和ε0的项各自相等,若A≠0,我们能够分别得到程函方程(Eikonal equation)(18)和方程(19),利用带有速度▽Φ的(19)的标量解B(t,x),方程(19)可以变成如下形式:

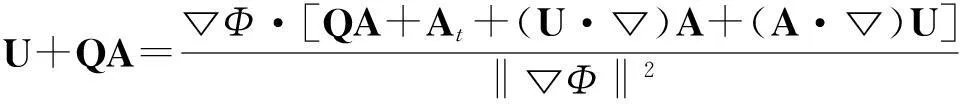
(24)

带有如下初值的方程(18)和(24)

Φ(0,x)=Φ0(x),A(0,x)=A0(x)

(25)

是偏微分方程系统,但它被更恰当地认为是一个沿着基本流形轨迹的常微分方程系统,解的分析相应的变得简单.我们把这个系统作为一个沿着粒子路径的常微分方程系统

(26)

并且

x(0)=x0.

(27)

粒子移动的时候,由U引起的向量A(t,x)的时间变化率(或者是总时间的导数,再或者是物质导数),如下:

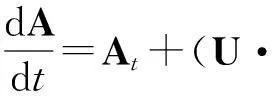
(28)

程函方程(Eikonal equation)(18)的梯度满足以下方程:

ξt+(U·▽)ξ+LTξ=0,

(29)

在这里,

(30)

由(28)可知,方程(29)变为以下形式:

(31)

正交性条件(21)的总时间导数满足:

(32)

由(32)和(29)可知,方程(24)右端的表达式可以简单化,由(28)可知,方程可以写成如下形式:

(33)

总之,考虑到ε的高阶项以及沿着基本流U(t,x)的粒子轨迹(26)-(27),向量A和ξ满足如下的微分方程组:

(34)

同时,带有如下初值条件:

ξ(0)=ξ0,A(0)=A0,A0·ξ0=0.

(35)

[9-11]中都得到常微分系统(26)-(27)和(34)-(35).基本流U(t,x)上的每一条轨迹都通过x0.

4 带有暗流的赤道水波的稳定性分析

第二节中给出的边缘波,粒子轨迹是显然的,因此,我们已经解决了系统(26),它的解具有式(5)的形式.现在,我们解决(34)中的第一个方程.区别于对t,(5)中雅可比矩阵(10),我们得到以下方程

(36)

这里L定义在(30).另一方面,区别于t,有如下关系

FTGT=Id,

(37)

G是F的逆矩阵,T代表矩阵转置,我们可以得到以下方程:

(38)

从而,系统(34)的第一个方程的一般形式解具有以下形式:

ξ(t)=GT(t).

(39)

由初值条件(35)可以得到下面的解:

ξ(t)=GT(t)FT(0)ξ0.

(40)

由(10)和(12)分别表示的矩阵F和G,这个解ξ变为:

(41)

这里ξ和θ与(11)的表达一样,因此,对于以下初值条件:

ξ0=(0,1,0)T,

(42)

可以得到下面的解:

ξ(t)=(0,1,0)T,∀t≥0.

(43)

把(43)代入系统(34)的第二个方程,变为以下形式:

(44)

由(36)可知,矩阵L可以被写成以下形式:

(45)

这里F,G分别来自于(10)和(12),进而,我们可以得到:

(46)

这表明速度扰动一直位于垂直于向量(0,1,0)T的平面.矩阵L依赖于t,从而,线性微分系统(44)是非自治的.不过,在[7,16]中,合适的变量变化能够提供一个容易控制的自治系统.利用矩阵L在(46)中的表示,方程(44)可以被写作:

(47)

其中

(48)

(49)

(50)

(51)

从上面我们得到区分t的第二个关系:

(52)

考虑规范基上的(51)中第一个关系以及(47),其中(A1(t),A2(t),A3(t))T是A(t)的元素,从(52)我们得到:

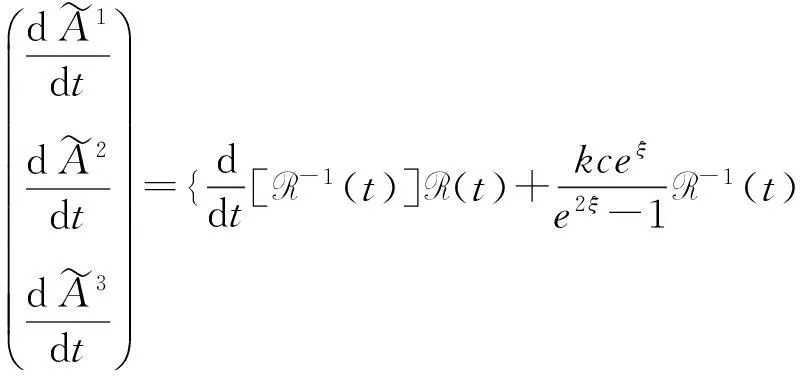
(53)

因此,在旋转基上,方程(47)变为

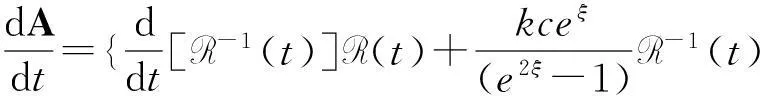
(54)

显而易见的是:

(55)

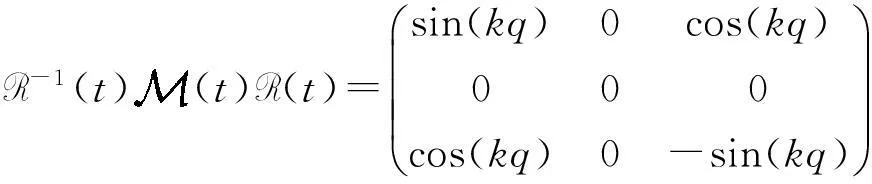
(56)

因此,方程(54)在旋转坐标下变为自治的,有如下形式:

(57)

其中含有不依赖于时间的矩阵:

(58)

(59)

综上所述,我们获得了以下结果.

定理1 如果(9)代表在Gerstner波下以速度c向西传播的恒流,当t→∞时,解以指数形式增长当且仅当向量(9)的非零部分满足如下条件:

(60)

定理2 如果把c带入(60),向量(9)的非零部分满足:

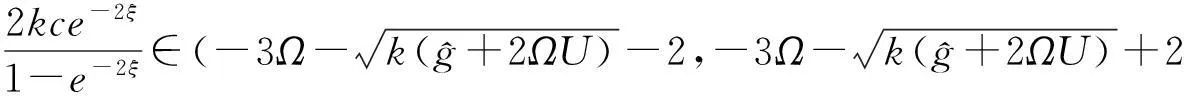
(61)

此外,由于U是常数,会影响向量(9)的不稳定区域,这时,我们可以忽略地球自转速度Ω,这时我们可以知道暗流不会影响向量(9)的不稳定区域,向量(9)的非零部分满足:

(62)

同时,我们知道,短波长的扰动随时间的增长率是(59)中的正根,即:

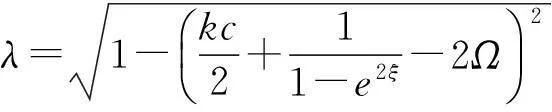
(63)

结论 本文中,通过使用短波扰动的方法,在拉格朗日坐标系中研究了f平面上带有暗流的赤道水波的稳定性.实际上,该结果可与f平面上不含暗流的水波进行比较,后发现,暗流的存在不影响赤道水波的不稳定区域.同时,我们可以用同样的方法去讨论f平面上其他的涡度矢量.

[1] GERSTNER F. Theorie der Wellen samt einer daraus abgeleiteten Theorie der Deichprofile [J]. Ann Phys,1809,2:412-445.

[2] RANKINE W J M. On the exact form of waves near the surface of deep water[J]. Philos Trans R Soc Lond A,1863,153:127-138.

[3] CONSTANTIN A. On the deep water wave motion[J]. J Phys,2001,34(7):1405-1417.

[4] CONSTANTIN A. Nonlinear Water Waves with Applications to Wave-Current Interactions and Tsunamis[J]. CBMS-NSF Regional Conference Series in Applied Mathematics,2011,81:321.

[5] HENRY D. On Gerstners water wave[J]. J Nonlinear Math Phys,2008,15(2):87-95.

[6] HSU H C. Some nonlinear internal equatorial waves with a strong underlying current[J]. App Math Lett,2014,34:1-6.

[7] CONSTANTIN A, GERNAIN P. Instability of some equatorially trapped waves[J]. J Geophys Res,2013,118(6):2802-2810.

[8] CONSTANTIN A. Some nonlinear, equatorially trapped, non-hydrostatic, internal geophysical waves[J]. J Phys Oceanogr,2014,44(2):781-789.

[9] BAYLY B J. Three-dimensional instabilities in quasi-two dimensional inviscid flows[C]//Nonlinear Wave Interactions in Fluids. New York:ASME,1987：71-77.

[10] FRIEDLANDER S, VISHIK M M. Instability criteria for the flow of an inviscid incompressible fluid[J]. Phys Rev Lett,1991,66(17):2204-2206.

[11] LIFSCHITZ A, HAMEIRI E. Local stability conditions in fluid dynamics[J]. Phys Fluids,1991,3(11):2644-2651.

[12] FRIEDLANDER S, YUDOVICH V. Instabilities in fluid motion[J]. Notices Amer Math Soc,1999,46:1358-1367.

[13] FRIEDLANDER S, LIPTON-LIFSCHITZ A. Localized instabilities in fluids[J]. Handbook of Mathematical Fluid Dynamics,2003,2:289-354.

[14] BAYLY B J, HOLM D D, LIFSCHITZ A. Three-dimensional stability of elliptical vortex columns in external strain flows[J]. Philos Trans R Soc Lond Ser A,1996,354(1709):895-926.

[15] LIFSCHITZ A. On the instability of three-dimensional flows or an ideal incompressible fluid[J]. Phys Lett A,1992,167(5):465-474.

[16] LEBLANC S. Local stability of Gerstner’s waves[J]. J Fluid Mech, 2004, 506: 245-254.

[17] CONSTANTIN A. An exact solution for equatorially trapped waves[J]. J Geophys Res,2012,117:5-29.

[18] PEDLOSKY J. Geophysical Fluid Dynamics[M].New York:Springer,1979.

[19] HSU H C. An exact soultion for equatorially waves[J]. Monatsh Math,2014,176:1-10.

[20] LIFCSHITZ A. On the instability of certain motions of an ideal incompressible fluid[J]. Adv in Appl Math,1994,15(4):404-436.

[21] FRIEDLANDER S, VISHIK M M. Instability criteria for steady flows of a perfect fluid[J]. Chaos,1992,2(3):455-460.

[22] CONSTANTIN A. The trajectories of particles in strokes waves[J]. Invent math,2006,166(3):523-535.

[23] MATIOC A V. An exact solution for geophysical equatorial edge waves over a sloping beach[J]. Phy A Math Theor,2012,45(36):1567-1587.

[24] IONESCU-KRUSE D. Instability of edge waves along a sloping beach[J]. J Diff Eqs,2014,256(12):3999-4012.

[25] HENRY D. An exact solution for equatorial geophysical water waves with an underlying current[J]. European J of Mechanics-B/Fluids,2013,38:18-21.

Stability of Equatorial Water Waves with an Underlying Current

LAN Tianzhu, CHEN Xiaohe, XU Yancong

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

In this paper, the stability of equatorial water waves in thef-plane with an underlying current described in Lagrangian fame-work is investigated by using the technology of short-wavelength perturbations. It is proved that the current does not influence the flow’s unstable region if the rotational speed of the earth is ignored. And an unstable region of a water waves in a certain speed is obtained.

Lagrangian framework; localized instability; short-wavelength method; equatorial water wave

2015-04-12

浙江省自然科学基金项目(LY13A010020);杭州师范大学科研基金项目(HNUEYT).

徐衍聪(1970—),男,副教授,博士,主要从事微分动力系统分支研究.E-mail:yancongx@163.com

10.3969/j.issn.1674-232X.2016.02.012

O175.29 MSC2010:35G20,35Q92

A

1674-232X(2016)02-0184-08