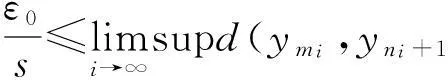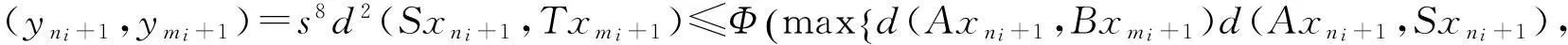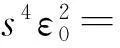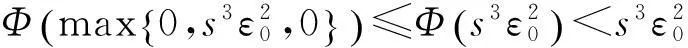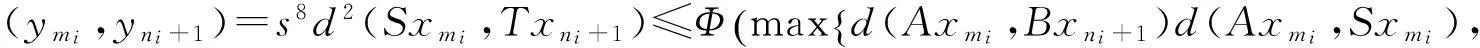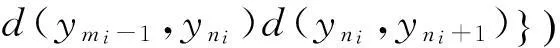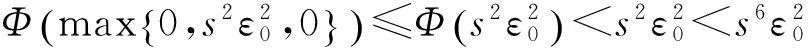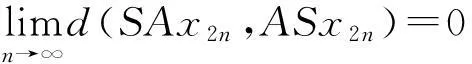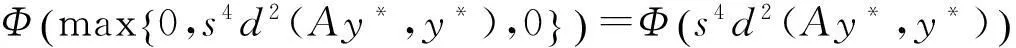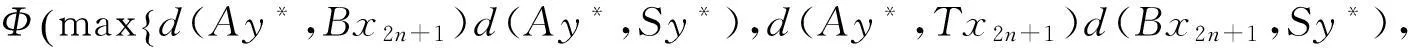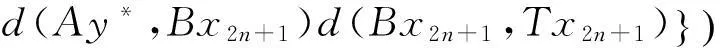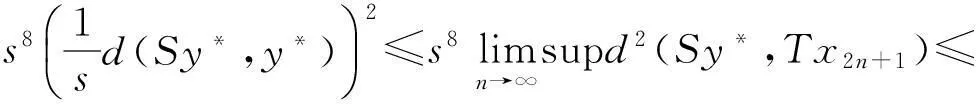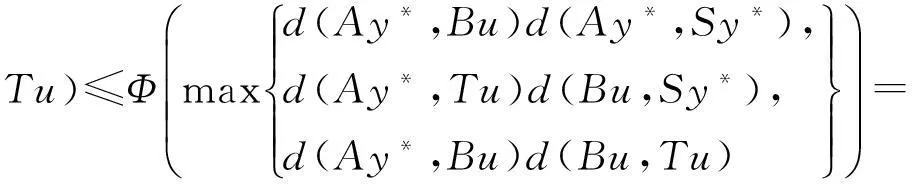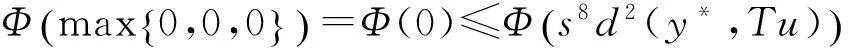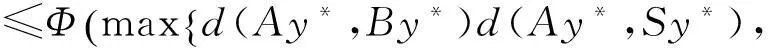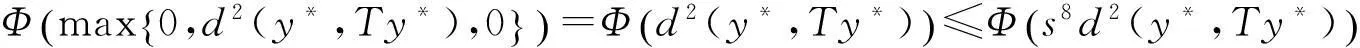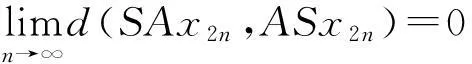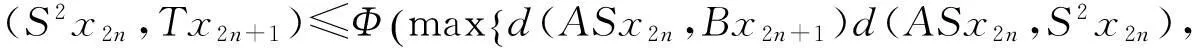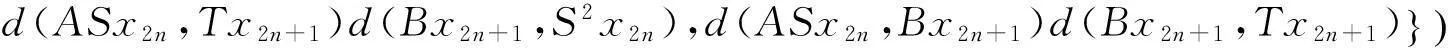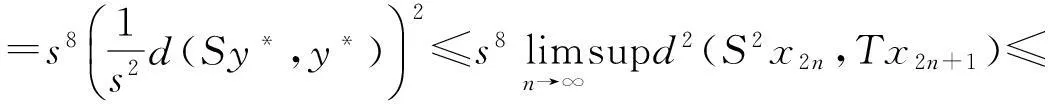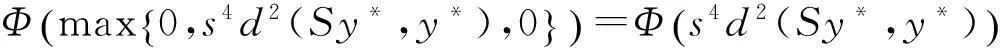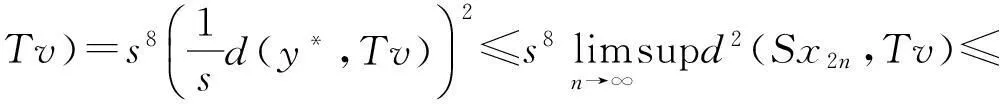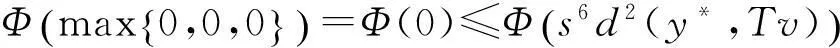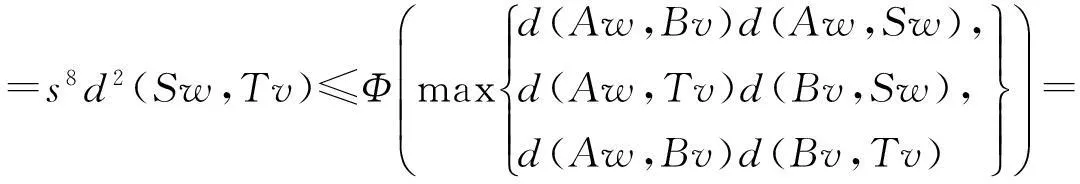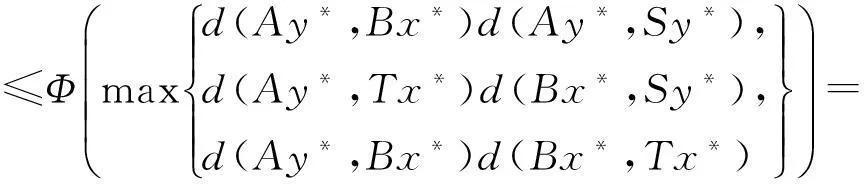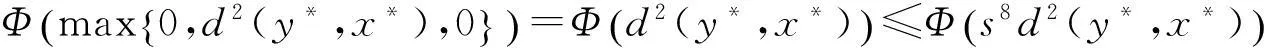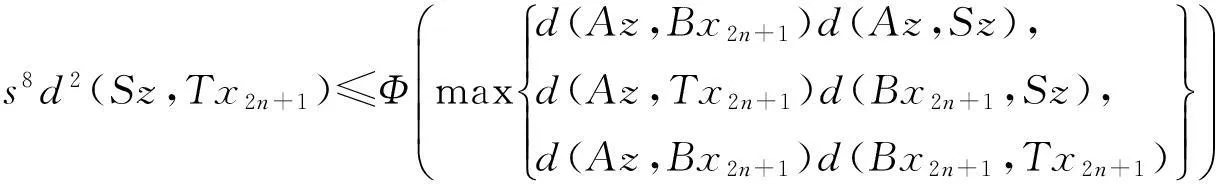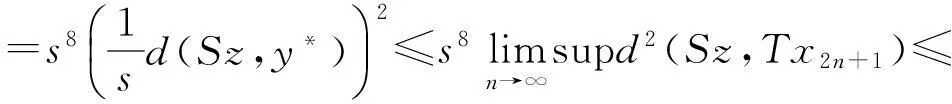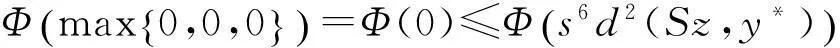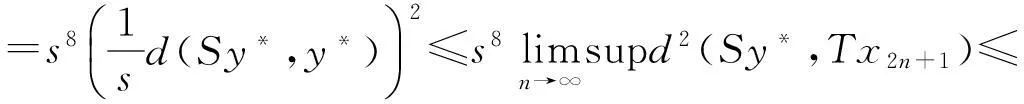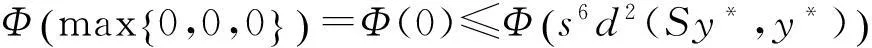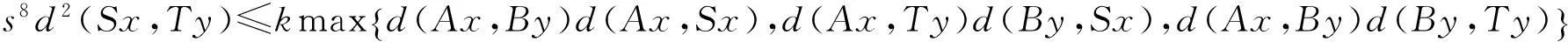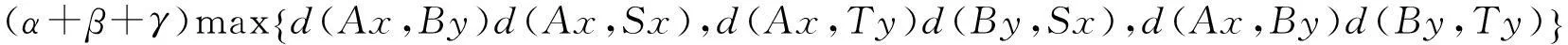b-度量空间中的一类平方型Φ-压缩映象的公共不动点定理

刘丽亚,谷 峰

(杭州师范大学应用数学研究所，杭州师范大学理学院，杭州 浙江 310036)

b-度量空间中的一类平方型Φ-压缩映象的公共不动点定理

刘丽亚,谷 峰

(杭州师范大学应用数学研究所，杭州师范大学理学院，杭州 浙江 310036)

利用b-度量空间中自映象对相容和弱相容条件,讨论了b-度量空间中一类平方型Φ-压缩映象公共不动点的存在性与唯一性问题,证明了一个新的公共不动点定理，改进和推广了某些已知结果.

b-度量空间; 相容映象对; 弱相容映象对; 平方型Φ-压缩映象; 公共不动点

1 引言和预备知识

在度量空间的框架下,张石生[1]和谷峰[2]研究了一类Φ-扩张型映象,在映象对可交换和相容的条件下,分别得到了3个映象和4个映象的公共不动点定理.后来,谷峰与何振华[3]讨论了一类Φ-压缩型映象的公共不动点问题,获得了一个新的公共不动点定理.本文受上述文献的启发,将问题放在由Czerwik[4]所提出的b-度量空间中加以考虑.我们在b-度量空间中研究了涉及4个映象的一类平方型Φ-压缩映象,在适当的条件下证明了一个新的公共不动点定理.由于b-度量空间包含一般的度量空间为特例,因此,该结果本质的改进和发展了前人的一些已知结果.

定义1[4]设X是一非空集,s≥1是一个给定的实数.称函数d:X×X→R+是集合X上的一个b-度量.若对∀x,y,z∈X,有以下条件满足：

(b1)d(x,y)=0⟺x=y; (b2)d(x,y)=d(y,x); (b3)d(x,z)≤s[d(x,y)+d(y,z)].

这时，称(X,d)是一个b-度量空间,称实数s为b-度量空间(X,d)的系数.

注1 度量空间一定是b-度量空间(s=1),反之,b-度量空间不一定是度量空间.反例可见文献[5].

定义2[6]设(X,d)是一个b-度量空间,点列{xn}⊂X.

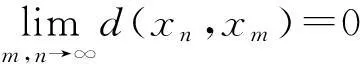
注2[7]在b-度量空间中:(i)收敛点列的极限是唯一的;(ii)每个收敛点列都是柯西列;(iii)一般情况下,b-度量不一定是连续的.

定义3[6]若b-度量空间(X,d)上每个Cauchy列都收敛,则称此b-度量空间为完备的b-度量空间.

引理1[8]设(X,d)是具有参数s≥1的b-度量空间,{xn}·{yn}⊂X分别收敛于X中的两点x和y.则有

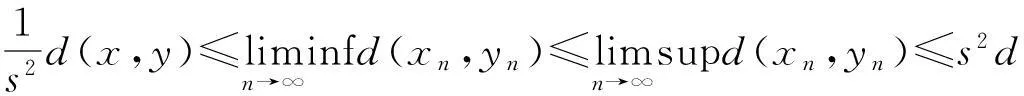
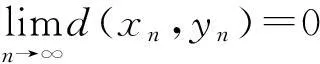
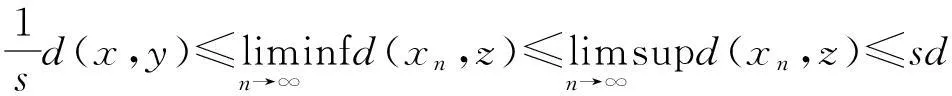
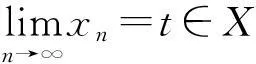
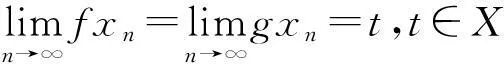
定义5[10]集合X上的自映象对(f,g)称为是弱相容的,如果

{t∈X:f(t)=g(t)}⊂{t∈X:fg(t)=gf(t)}

定义6[1]称函数Φ满足条件(Φ),如果函数Φ满足以下条件:

(Φ):Φ:[0,∞)→[0,∞)是连续的和对t不减的,且Φ(t)0.

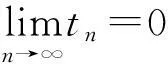
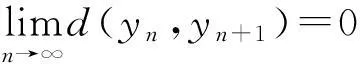
(i)mi>ni+1,ni→∞(i→∞);(ii)d(ymi,yni)>ε0;d(ymi-1,yni)≤ε0,i=1,2,3,….

证明 与文献[1]中引理7.4.4的证明完全类同,这里略去.

2 主要结果

定理1 设S,T,A,B是完备b-度量空间(X,d)中的4个自映象,且满足以下条件:

(i)S(X)⊂B(X),T(X)⊂A(X);(ii)∀x,y∈X,有

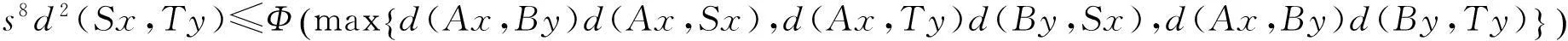
其中Φ满足条件(Φ).如果以下条件之一被满足,则S,T,A,B有唯一公共不动点.

1)S,A之一连续,且(S,A)相容,(T,B)弱相容;2)T,B之一连续,且(S,A)弱相容,(T,B)相容;3)A,B之一为满射,且(S,A)和(T,B)都弱相容.

证明 任取x0∈X,因S(X)⊂B(X),T(X)⊂A(X),故存在{xn},{yn}⊂X,使得

y2n=Sx2n=Bx2n+1,y2n+1=Tx2n+1=Ax2n+2,n=0,1,2,3,…

下证

露骨料透水混凝土是由粗骨料、高标号水泥、水、强化剂、外加剂等经一定比例调配拌制而成的一种多孔轻质的新型环保地面铺装材料。与传统混凝土相比，透水混凝土多采用单粒径的粗骨料作为混凝土的主体，配以水泥净浆或者少量细骨料砂浆作为粘接剂，包裹在粗骨料颗粒的表面，形成孔隙均匀分布的蜂窝状结构，结构模型如图1所示。普通混凝土结构模型如图2所示。

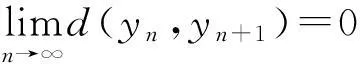
(1)

事实上,由条件(ii)可知

(2)

如果d(y2n-2,y2n-1)0(否则有d(y2n-2,y2n-1)<0,矛盾).于是由式(2)和定义6得

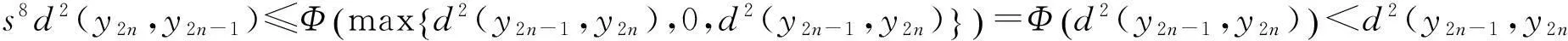
出现矛盾,因此必有d(y2n-1,y2n)≤d(y2n-1,y2n-2)成立.于是,从Φ的递增性和式(2)可得

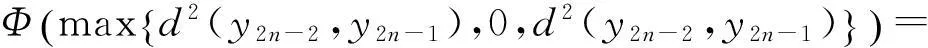
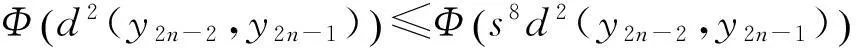
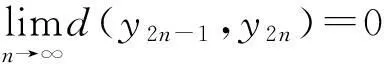
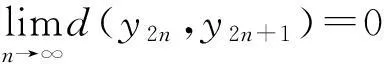
下面证明{yn}是X中的Cauchy列.若不然,由引理4知,必存在某一ε0>0和正整数列{mi},{ni},使得:(a)mi>ni+1,ni→∞(i→∞);(b)d(ymi,yni)>ε0,d(ymi-1,yni)≤ε0,i=1,2,3,….

则由三角不等式和(b)得

d(ymi,yni)≤sd(ymi,ymi-1)+sd(ymi-1,yni)≤sd(ymi,ymi-1)+sε0.

(3)

d(ymi+1,yni)≤sd(ymi+1,ymi-1)+sd(ymi-1,yni)≤s2d(ymi+1,ymi)+s2d(ymi,ymi-1)+sε0.

(4)

sd(ymi,ymi-1)+s2ε0+s2d(yni,yni+1).

(5)

d(ymi-1,yni+1)≤sd(ymi-1,yni)+sd(yni,yni+1)≤sε0+sd(yni,yni+1).

(6)

在式(3)(4)(5)和(6)两端取上极限,并利用式(1)得

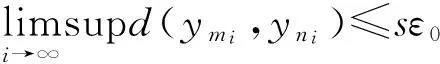
(7)

(8)

(9)

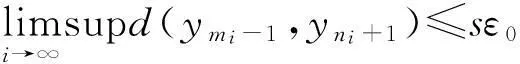
(10)

再由三角不等式和(b)得ε0

sd(ymi,ymi+1)+s2d(ymi+1,yni+1)+s2d(yni+1,yni).

(11)

ε0

(12)

在式(11)(12)两端取上极限,并利用式(1)得

(13)

(14)

下面分4种情况进行讨论.

(I)当mi为偶数,ni为奇数的情形.此时由条件(ii)有

于上式两端各项取上极限,并利用式(1)(7)(8)(9)(13)和Φ(t)的性质,得

此为矛盾.

(II)当mi,ni都为偶数的情形.此时由条件(ii)有

于上式两端各项取上极限,并利用式(1)(7)(10)(14)(b)和Φ(t)的性质,得

此为矛盾.

(III)当mi,ni同为奇数,(IV)mi为奇数,ni为偶数的情形,与(I)和(II)同理可引出类似的矛盾.这些矛盾说明{yn}是X中的Cauchy列.

因X完备,故存在y*∈X,使得yn→y*(n→∞),于是子列{y2n-1}和{y2n}也都收敛于y*,即Ax2n=y2n-1→y*,Sx2n=y2n→y*(n→∞).

1)设S,A之一连续且,(S,A)相容,(T,B)弱相容.

于上式两边取上极限,并利用引理1得

于是由引理3(i)可知,有s4d2(Ay*,y*)=0,进而Ay*=y*.再由条件(ii)有

对上式两边取上极限,使用引理1,Ay*=y*和Φ的递增性,得

由此及引理3(i)可知,有s4d2(Sy*,y*)=0,进而可得Sy*=y*.于是y*=Sy*=Ay*.

由此及引理3(i)可知,有s8d2(y*,Tu)=0,进而y*=Tu.

因(T,B)弱相容,故Ty*=TBu=BTu=By*.

下证Ty*=y*.事实上,由条件(ii)和Φ的递增性可得

故由引理3(i)可知,s8d2(y*,Ty*)=0,即y*=Ty*.于是y*=Ty*=By*.

综上,我们得y*=Sy*=Ay*=Ty*=By*,即y*是S,T,A,B的公共不动点.

于上式两端取上极限,并使用引理1和函数Φ的性质,得

于是由引理3(i)可知s4d2(Sy*,y*)=0,进而可得Sy*=y*.

下证Ay*=y*,事实上,由Sy*=y*及SX⊂BX知,∃v∈X使Bv=Sy*=y*.使用条件(ii)得

s8d2(Sx2n,Tv)≤

对上式两端取上极限,并使用引理1和Φ的递增性质,得

由此及引理3(i)可知,s6d2(y*,Tv)=0,即y*=Tv.于是Bv=Tv=y*.

由y*=Tv∈TX⊂AX可知,∃w∈X使Tv=Aw=y*.再使用条件(ii)得

由此及引理3(i)可知,s8d2(Sw,y*)=0,即Sw=y*.于是y*=Sw=Aw.因(A,S)弱相容,故y*=Sy*=SAw=ASw=Ay*.

对于y*=Ty*=By*的证明,与A连续时相应部分的证明完全相同,这里省略.

综上我们有y*=Sy*=Ay*=Ty*=By*,即y*是S,T,A,B的公共不动点.

下证公共不动点唯一.设x*也是S,T,A,B的一个公共不动点,则由条件(ii)有

由此及引理3(i)可知,s8d2(y*,x*)=0,即y*=x*.于是y*是S,T,A,B的唯一公共不动点.

2)当B,T之一连续,(S,A)弱相容,(T,B)相容时,类似1)可证.

3)设A,B之一为满射,且(S,A)和(T,B)都弱相容.

如果A是满射,则对y*∈X,∃z∈X使Az=y*.由条件(ii)得

上式中令n→∞取上极限,并利用引理1得

(15)

由此及引理3(i)可知,s6d2(Sz,y*)=0,即Sz=y*.于是Sz=Az=y*.

又由(S,A)弱相容.故Sy*=SAz=ASz=Ay*.

下证Sy*=y*.以y*代替式(15)中的z,可得

由此及引理3(i)可知,s6d2(Sy*,y*)=0,即Sy*=y*,于是Ay*=Sy*=y*.

对于y*=Ty*=By*的证明,与1)中相应部分的证明完全相同,这里省略.

至此,我们证明了y*=Sy*=Ay*=Ty*=By*,即y*是S,T,A,B的公共不动点.

公共不动点的唯一性与1)中的证明相同.

当B是满射时同理可证y*是S,T,A,B的唯一公共不动点.至此定理1获证.

注3 由于度量空间一定是b-度量空间,故定理1扩展了文献[3]的主要结果.

推论1 设S,T,A,B是完备b-度量空间(X,d)中的4个自映象,满足条件S(X)⊂B(X)和T(X)⊂A(X),且∀x,y∈X,都有

其中k∈(0,1).如果以下条件之一被满足,则S,T,A,B有唯一公共不动点.

1)S,A之一连续,且(S,A)相容,(T,B)弱相容;2)T,B之一连续,且(S,A)弱相容,(T,B)相容;3)A,B之一为满射,且(S,A)和(T,B)都弱相容.

证明 在定理1中取Φ(t)=kt即得.

推论2 设S,T,A,B是完备b-度量空间(X,d)中的4个自映象,满足条件S(X)⊂B(X)和T(X)⊂A(X),且∀x,y∈X,都有

s8d2(Sx,Ty)≤αd(Ax,By)d(Ax,Sx)+βd(Ax,Ty)d(By,Sx)+γd(Ax,By)d(By,Ty).

其中α,β,γ≥0,0<α+β+γ<0.如果以下条件之一被满足,S,T,A,B有唯一公共不动点.

1)S,A之一连续,且(S,A)相容,(T,B)弱相容;2)T,B之一连续,且(S,A)弱相容,(T,B)相容;3)A,B之一为满射,且(S,A)和(T,B)都弱相容.

证明 由条件(ii)可得

s8d2(Sx,Ty)≤αd(Ax,By)d(Ax,Sx)+βd(Ax,Ty)d(By,Sx)+γd(Ax,By)d(By,Ty)≤

考虑到0<α+β+γ<1,则推论2的结论由推论1即得.

注4 推论1和推论2将度量空间中的相应结果扩展到更广泛的b-度量空间中.

[1] 张石生.不动点理论及其应用[M].重庆:重庆出版社,1984.

[2] 谷峰.关于Φ扩张相容映象的公共不动点定理[J].宝鸡文理学院学报(自然科学版),2001,21(3):176-179.

[3] 谷峰,何振华.一类平方型Φ-压缩映象的公共不动点定理[J].商丘师范学院学报,2006,22(5):27-32.

[4] CZERWIK S. Contraction mappings in b-metric space[J]. Acta Math Inform Univ Ostraviensis,1993,1(1):5-11.

[5] AKKOUCHI M. A common fixed point theorems for expansive mappings under strict implicit conditions on b-metric spaces[J]. Acta Univ Palack Olomuc Fac Rerum Natur Math,2011,50(1):5-15.

[6] BORICEANU M. Strict fixed point theorems for multivalued operators in b-metric spaces[J]. Int J Mod Math,2009,4(3):285-301.

[7] BORICEANU M. Fixed point theory for multivalued contraction on a set with two b-metrics[J].Creative Math,2008,17:326-332.

[8] AGHAJANI A, ABBAS M, ROSHAN J R. Common fixed point of generalized weak contractive mappings in partially ordered b-metric spaces[J]. Math Slovaca,2014,64(4):941-960.

[9] ROSHAN J R, SHOBKOLAEI N, SEDGHI S, et al. Common fixed point of four maps in b-metric spaces[J]. Hacettepe Journal of Mathematics and Statistics,2014,43(4):613-624.

[10] JUNGCK G. Common fixed points for non-continuous nonself mappings on a nonmeric spaces[J]. Far East J Math Sci,1996,4(2):199-212.

The Common Fixed Point Theorem for a Class of Twice Power TypeΦ-contractive Mapping inb-metric Spaces

LIU Liya, GU Feng

(Institute of Applied Mathematics, School of Science, Hangzhou Normal University, Hangzhou 310036, China)

By using the compatible and weak compatible conditions of self-mapping pair inb-metric spaces, the existence and uniqueness of common fixed point for a class of twice power typeΦ-contractive mappings inb-metric spaces is discussed. A new common fixed theorem is obtained.

b-metric spaces; compatible mapping pair; weak compatible mapping pair; twice power typeΦ-contractive mapping; common fixed point

2015-06-10

国家自然科学基金项目(11071169);浙江省自然科学基金项目(Y6110287).

谷 峰(1960—), 男, 教授, 主要从事泛函分析及其应用研究. E-mail: gufeng99@sohu.com

10.3969/j.issn.1674-232X.2016.02.010

O177.91 MSC2010:47H10,54H25

A

1674-232X(2016)02-0171-07