紧致插值曲线CIP方法及其应用

赵西增，刘必劲，梁书秀，孙昭晨

（1浙江大学海洋学院，浙江舟山316021；2福建省海洋预报台，福州350003；3大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

紧致插值曲线CIP方法及其应用

赵西增1，刘必劲2，梁书秀3，孙昭晨3

（1浙江大学海洋学院，浙江舟山316021；2福建省海洋预报台，福州350003；3大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

波浪与建筑物的相互作用过程会涉及到波浪破碎、水气掺混和结构物的动力响应等复杂过程，对数值算法提出了更高要求。文章基于紧致插值曲线CIP（Constrained Interpolation Profile）方法建立了可模拟波浪破碎、翻滚等自由面大变形流动问题的数学模型。模型以CIP方法为流场基本求解器，离散了纳维-斯托克斯（Navier-Stokes:N-S）方程，同时还以CIP方法捕捉了自由面，通过多相流理论描述了流-固-气之间的相互作用。对强非线性自由表面流动问题的典型算例溃坝问题开展了数值模拟，并通过与他人实验结果的比较验证了模型的有效性。最后开展了极端波浪对浮式结构冲击过程的模拟，准确地预测了甲板上浪和结构的动力响应等问题。

CIP方法；自由面流动；高阶差分；极端波浪；流固耦合

0 引 言

极端波浪与海上建筑物相互作用过程会涉及到波面破碎、翻滚、水气掺混和结构物动力响应等强非线性自由面大变形问题，开发适合上述现象的CFD模型，准确预测波浪力和结构响应，对海上结构设计和安全防护等问题具有重要的工程应用价值。

由于上述问题的复杂性，传统的基于势流理论的边界元和有限元方法不再适用，就要考虑基于N-S方程的数值方法。对N-S方程的网格离散方法中，有限差分法是计算机数值模拟最早采用的方法，并已被验证为有效方法之一。为了得到稳定的流场信息，对N-S方程的对流项采用迎风格式求解是合适的选择之一。为了消除迎风格式带来的数值耗散和较低的精度，高精度的差分格式应运而生。其中，CIP方法是Takewaki等人[1]于20世纪80年代中期提出并发展起来，用于求解双曲型偏微分方程的一种有效的数值计算方法[2]，已被应用于一些流体界面以及流体内部交叉问题中所遇到的复杂形状的移动界面问题[3-7]。其基本原理是基于空间网格点的变量值及其空间导数值，利用三次多项式进行插值近似，反演出网格单元内部变量的真实信息，得到时间和空间上都是三阶精度的显式格式。为了更好地解释CIP方法，我们考虑简单的常系数一维对流方程：

其中：u为大于零的常数。此类最简单的双曲线偏微分方程可用不同的差分方法求解。下面将给出CIP方法的工作原理。图1（a）-（c）给出了一阶迎风差分方法的工作原理，对于一阶差分格式来说，它利用直线的方式联立相邻两个节点的信息来工作（图1（c）），而忽略了网格内部的信息，会引起较大的数值耗散。为了真实地再现网格内部的信息，我们需要求助于高阶差分，常规高阶差分的建立需要更多网格点的信息。而在图1（d）中，CIP方法采用一种独特的方式，在一个网格内实现了高阶差分格式，通过利用空间网格点的变量值及其空间导数值，来描述该网格内的信息，可逼真地再现网格内的信息。

图1 CIP方程基本原理Fig.1 Principle of CIP method

通过对方程（1）求关于x的偏导，我们得到如下的空间导数方程：

在n+1时刻的单元格剖面函数fn+1可以通过将n时刻的剖面函数fn平移-uΔt得到，函数f和g的时间演变可以通过下面的拉格朗日变换得到（如图2所示）：

图2 半拉格朗日方法的CIP格式Fig.2 CIP scheme as a semi-Lagrangian method

因此，从CIP对流格式采用了拉格朗日常量解法（Lagrangian invariant solution）的角度来看，CIP对流格式又称为半拉格朗日方法，如图1所示。公式（4）中的四个未知系数可由已知量通过下列关系式来确定：

最初的CIP是“Cubic Interpolation Propagation”的缩写，但是随着CIP方法的发展，研究者相继提出了很多其它阶数的多项式表达的格式，最近它多被解释为“Constrained Interpolation Profile”。 CIP方法采用一种独特的方式，在一个网格内实现了高阶差分格式，使得本文的数值模型可以应用于复杂流动问题的模拟，这也是本文所采用的差分方法与其他方法的不同之处。

本文不但以CIP方法作为N-S方程的基本求解器，并通过CIP方法重构了自由面，通过多相流的方式处理了固液气的相互作用问题，建立了可适用于强非线性自由表面流动的二维数学模型。首先开展了矩形波和刚体旋转问题的模拟，验证CIP方法在求解对流方程和捕捉自由面问题的能力；然后通过开展溃坝问题的模拟并与实验结果做比较,验证了模型对自由面大变形问题的适用性。最后基于该模型开展了极端波浪对浮式结构冲击过程的数值模拟，预测了甲板上浪和结构的动力响应等问题。

1 数学模型介绍

1.1 控制方程

本流场模型，以不可压缩流体为研究对象，以二维N-S方程为控制方程，其矢量形式为：

连续方程

为了把CIP方法应用于对流方程，对方程（7）取空间导数，可得到下面的形式：

模型在直角笛卡尔系统下建模，采用多相流理论处理固-气-液的相互作用，各相满足下面的方程

其中：m=1,2,3，φ1为液体相，φ2为气体相，φ3为固体相，在一个网格内满足φ1+φ2+φ3=1。固体相的处理采用独特的虚拟粒子法得到，具体可参考文献[4]。网格内的流体特性可用下式来表示：

其中：λ为密度ρ或者粘性系数μ。在程序中固体和液体按同相处理，二者的物理参数设置为相同，可保证二者之间的有效结合和数值计算的稳定，这也是本模型与其他方法不同的地方。

1.2 时间积分格式

在对动量方程进行时间积分时采用了分步算法。首先忽略扩散项和压力项，计算只考虑对流项的中间速度；其次求解扩散项；然后求解压力方程，计算下一时间步的压力；最后考虑压力梯度项，计算速度的最后值。设Δt为时间步长，在t=nΔt到t=（n+1）Δt时刻的计算时间内，具体的时间积分过程如下：

（1）对流项（I）

通过CIP方程可得到方程的解为：

其中：“*”为对流项计算结束后的中间时间标志。对流项的求解通过CIP方法[2]实现，同时模型中自由面的重构也通过该方法实现，这样在程序设计的时候就减少了相应的工作量。

（2）非对流项（I）

下面进入扩散项的计算：

扩散项的时间离散采用显示格式，中间速度可表示为下面的形式：

其中：方程（13-14）的空间离散采用中心差分格式。

（3）非对流项（II）

下一步进入压力和速度的匹配：

通过对方程（15a）取散度，并引入连续方程，可得到如下形式的泊松方程：

泊松方程的求解通过SOR迭代得到。

考虑动量方程的压力梯度项，计算速度的最终值，计算式为：

根据（9）式和（10）式进行自由面和网格内流体信息的更新，然后返回到步骤1，这样就完成了整个计算过程，一直到设定的步骤结束。

2 模型验证

2.1 矩形波的传播

图3给出了对流方程（11a）（u>0）采用不同差分方法得到的计算结果，分别为迎风格式、Lax方法、Lax-Wendroff格式和CIP方法。初始条件如下：在计算中，区间[-1，1]分为200个计算网格，即每个网格长度为0.01，对流参数u为0.5，时间步长为0.01 s，CFL数为0.25，总时间为4 s。左右边界为周期边界，即经过4 s之后原始波形刚好运动一个周期回到初始位置。图3每幅图中的虚线为理论值，实线为模拟结果。迎风格式和Lax格式均为时间一阶格式。图3（a）、（b）可看出其波形失真严重,所有的峰值信息都已经趋于平滑化，几乎已经丧失了波形的特征；而时间空间均为二阶的Lax-Wendroff格式虽然保持了一定的峰值信息，但是可以看出其受震荡非常剧烈，同样有着波形失真的问题。反观时间空间均为三阶的CIP方法，经过了一个周期的运动之后，其对原始波形的保持相当良好，仅在高斯波和三角波处出现了略微的峰值损失以及在矩形波和半椭圆波边缘梯度较大处出现了轻微的震荡。虽然CIP方法也存在着一些震荡，但是其震荡被限制在一个很小的区间内，得到的界面十分紧致。

图3 不同差分格式的一维的对流验证算例结果（虚线为理论值，实线为计算值）Fig.3 Validation of different finite difference methods for an advection equation

2.2 刚体旋转（Zalesak问题[8]）

旋转流场信息为：u=（y-0.5,0.5-x），其中时间步长Δt=2π/628。图4中给出了采用CIP作为自由面捕捉方式，刚体旋转问题的模拟结果[8]，并分析了网格大小的影响:网格数50×50、100×100、200×200和500×500。刚体的边界通过密度函数φ=0.05，0.5和0.95来表示。从图可知，当采用粗网格时，刚体的整体形状也具有较好的保持性，与理论结果（虚线）相比，刚体的边界变得模糊，也就是说刚体的边界在变“厚”，刚体边界失真严重。比较网格的大小对结果的影响可知，细网格具有较高计算精度。从上面两个算例可知，CIP方法不但可用于处理动量方程的对流项，同时也可用于自由面的重构。

图4 刚体旋转Fig.4 Results of Zalesak's problem after one rotation

2.3 溃坝问题

溃坝流动作为一种典型的自由表面流动，存在移动边界和复杂的大变形问题，一直是计算流体力学领域的一大难题，对数值模型具有较高的要求。下面将开展溃坝问题的模拟，分析本模型对该类问题的处理能力，并把模拟结果与他人实验结果[9-10]作比较。

初始条件如下：初始水体的几何尺寸为L×2L，计算域的大小为4L×4L，L=14.6 cm，如图5所示。初始时刻水体被挡板挡住，处于静平衡状态，t=0.0 s时刻挡板被迅速释放，计算开始。数值模型的边界条件采用不可滑移边界条件，水的密度为1 000 kg/m3，运动黏性系数μ=1.0×10-5m2/s，重力加速度为9.80 m2/s。

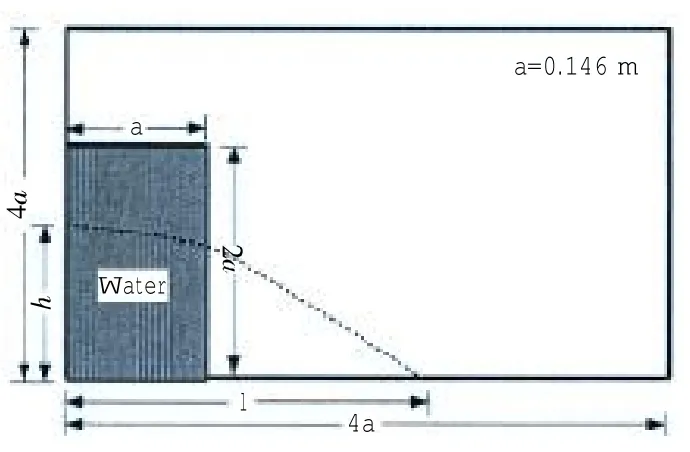
图5 溃坝问题的初始情况Fig.5 Initial condition of dam breaking

图6 数值与实验结果比较Fig.6 Comparison of the free surface between computation and experimental data

图6给出了t<1.0 s，不同时刻溃坝模型的实验[9]和模拟结果的比较。从图6可看到，在t=0.2 s时，水体已经坍塌，水体前缘沿着水槽底面迅速向右侧移动。随着时间的发展，水体前端到达右侧壁面，由于直墙的存在，水面像射流一样发生转向并开始上升，同时伴有水花的飞溅，在t=0.4 s的图中可看到水面沿着右侧壁面的上升。然后水头到达最高点，直到t=0.6 s左右，在重力的作用下开始下落,并与从底部向上运动的水流汇集在一起，水面出现隆起。下落的水体像自由落体一样砸入底部水体内，水面发生翻卷、破碎,随后翻卷的水面再次入水，撞击出一个水柱，并包裹着一定的空气，冲向左侧壁面（t=1.0 s）。

图7给出了数值结果和实验结果的定量比较，将水体的前段水头位置和左侧壁面高度与实验结果进行了对比，实验数据来自Koshizuka[9]及Martin和Moyce[10]，同时还给出了网格大小、时间步长的模拟结果。从图可知，模拟结果与实验结果吻合较好，除了底部水头前沿的位置比试验结果稍微大一些，这主要是由于在模型中没有考虑表面张力和底部壁面的影响引起的，而网格大小和时间步长对模拟结果的影响可忽略不计。

图7 水头位置比较Fig.7 Comparison of the water front postion

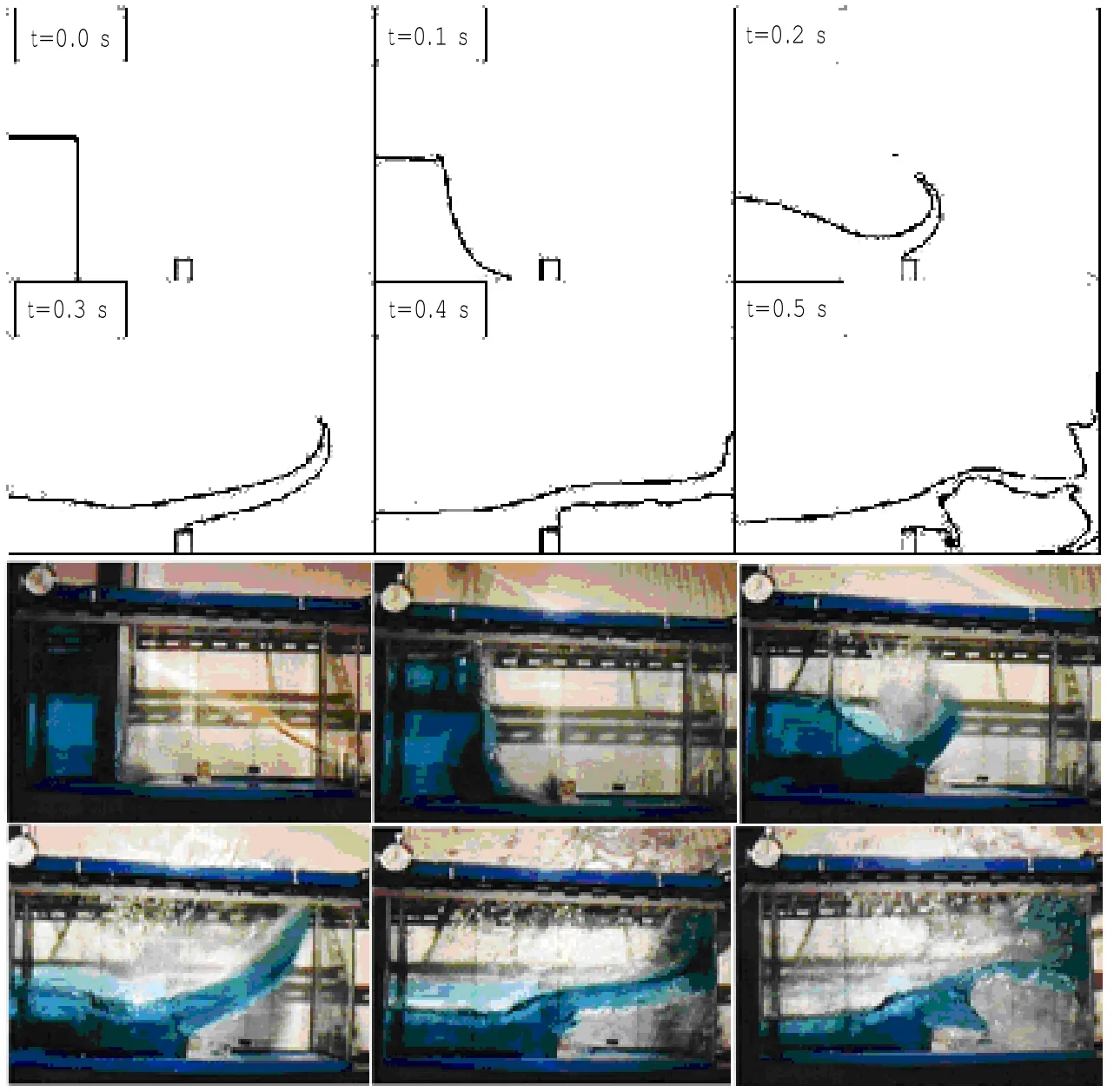
图8 数值与实验结果比较Fig.8 Comparison of the free surface between computation and experimental data

另外一个更有意思的溃坝问题是在流动的前方有障碍物存在的情况，问题将会变得更加复杂。图8给出了实验结果和数值结果的比较。从图8可知在水头没有到达障碍物之前和普通的溃坝并无二样，t=0.2 s时，由于障碍物的存在，水头吐出“水舌”；t=0.4 s时，溃坝流在障碍物与远端的壁面之间搭建了水墙，同时部分空气被包裹在里面；随着时间的发展，被包围的空气有冲出重围的欲望，同时在重力作用下，水墙开始崩坏，此时障碍物附近再次冒出“水舌”。上述有趣的物理现象在数值模拟中都可观察到，同时自由面与实验结果相比也有很好的一致性。

3 模型应用

为了更好地验证本模型的有效性和实用性，将把其应用于极端波浪对浮体作用问题的模拟。

图9 实验布置和测量设备Fig.9 Schematic of experimental setup

表1 模型参数Tab.1 Main parameter of the body model(m)

实验在日本九州大学应用力学研究所的波浪水槽内完成，实验布置图和浮体参数见图9和表1。本文只是考虑了浮体的升沉（heave）和旋转（pitch）两自由度的运动，具体的实验说明见文献[6]。极端波浪通过波浪聚焦方式得到，由波的色散性可知，波群中不同波长的波浪具有不同的传播速度，如果慢速传播的短波在快速传播的长波前面,那么随着相位的发展，在特定时刻和特定地点长波将会超越短波，进而引起波浪能量的汇聚。初始波面通过线性叠加给出：聚焦波幅A=0.05 m，谱峰周期Tp=1.2 s，水深h=0.4 m，频率范围（0.6，1.6），频率分隔数Nf=29，各组成波均匀分布在频率范围内，聚焦位置Xp=7.0 m，聚焦时间Tp=20 s，总的模拟时间30 s。

图10 波面时间历程Fig.10 Comparison of wave elevations along the tank between computation and physical results

图10-11给出了模拟结果与实验结果的比较，并对相关数据做了无因次处理。图10中给出了水槽内不同位置处的波面时间历程曲线，分别为聚焦位置及其前后两米的结果。图11给出了结构物的升沉运动、转动及结构前两米的波面时间历程。从图上可知，模拟结果与实验结果具有良好的一致性。由于极端波浪的存在，结构物会产生较大的运动响应，特别是转动问题，最大的转角接近10°。最后在图12中给出了结构物周围的波面情况和浮体位置与实验结果的比较，二者具有较好的一致性，说明本模型基本再现了极端波浪对结构物的作用过程。图12中再现了极端波浪对结构物完整的作用过程，首先波浪接近浮体，后形成沿x方向高速运动的浅层水流（见图t=20.0 s）；经过很短的时间，水流冲击到上层结构的直立墙，产生很大的冲击压力，并沿着直立壁向上爬升，直到重力作用克服上升的动量（见图t=20.4 s）；之后，水流开始反向运动，下降的水体会对浮体的产生巨大的作用力，使得结构物产生逆时针方向的力矩，结构出现较大的转动响应，在上述的作用过程中还存在复杂的水气掺混现象的发生（t=20.6 s），同时可知，甲板上浪的后期作用过程较复杂，这主要是由于波浪破碎引起的水气掺混引起的。比较上述甲板上浪问题和溃坝问题，可发现二者具有诸多相似性，都包含有以下几个过程：上浪、冲击、射流、翻滚、水气掺混等过程。

图11 结构响应数值结果与实验数据的比较Fig.11 Comparison of body response between computation and physical results

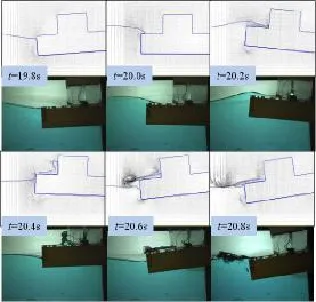
图12 结构物周围的流场信息和浮体位置Fig.12 Comparison of free surface and body position for extreme waves:Tw=1.2 s,A=0.05 m

4 结 论

本文基于高阶差分CIP方法建立了可模拟强非线性自由表面流动的二维数学模型，模型中CIP方法不但离散了N-S方程，而且捕捉了自由面；

通过开展矩形波的模拟，验证了CIP方法求解对流方程的优势，其采用较少的网格达到了高阶差分的计算精度；

采用CIP方法作为自由面捕捉方法，开展了刚体旋转问题的模拟研究，结果表明CIP方法具有自由面捕捉的能力；

开展了溃坝流动的数值模拟,完整地再现了溃坝流与壁面相互作用而产生的水花飞溅、水流反弹、自由表面剧烈变形等多种复杂的强非线性自由表面物理现象；

最后将模型应用于极端波浪与浮式结构相互作用的研究中，主要分析聚焦波面、浮体的动力响应以及波浪与结构物相互作用过程中的复杂流场结构等问题。由于极端波浪的出现，浮体出现较大转动角度的的响应。另外，分析结果表明甲板上浪过程与溃坝问题具有诸多相似性。

数值模拟结果与试验观察结果良好一致性的比较，验证了开发的数学模型的可靠性和计算结果的准确性。

[1]Takewaki H,Nishiguchi A,Yabe T.Cubic interpolated pseudo-particle method(CIP)for solving hperbolic-type equations [J].Journal of Computational Physics,1985,61:261-268.

[2]Yabe T,Xiao F,Utsumi T.The constrained interpolation profile method for multiphase analysis[J].Journal of Computational Physics,2001,169:556-593.

[3]Zhao X Z,Ye Z T,Fu Y N.Green water loading on a floating structure with degree of freedom effects[J].Journal of Marine Science and Technology,2014,19:302-313.

[4]Zhao X Z,Gao Y Y,Cao F F,Wang X G.Numerical modeling of wave interactions with coastal structures by a constrained interpolation profile/immersed boundary method[J].Int.Journal for Numerical Methods in Fluids,2015,doi:10.1002/fld. 4184.

[5]Zhao X Z,Ye Z T,Fu Y N.A CIP-based numerical simulation of freak wave impact on a floating body[J].Ocean Engineering,2014,87:50-63.

[6]Zhao X Z,Hu C H.Numerical and experimental study on a 2-D floating body under extreme wave conditions[J].Applied Ocean Research,2012,35:1-13.

[7]Cao F F,Zhao X Z.Nonlinear dynamic behaviors of a floating structure in focused waves[J].China Ocean Engineering, 2015,29(6):807-820.

[8]Zalesak S T.Fully multi-dimensional flux corrected transport algorithm for fluid flow[J].Journal of Computational Physics, 1979,31:335-362.

[9]Koshizuka S,Oka Y.Moving-particle semi-implicit method for fragmentation of incompressible fluid[J].Nuclear Science Engineering,1996,123(3):421-434.

[10]Martin J C,Moyce W J.An experimental study of the collapse of liquid columns on a rigid horizontal plane[J].Philosophical Transactions of the Royal Society A,1952,224:312-324.

Constrained Interpolation Profile(CIP) method and its application

ZHAO Xi-zeng1,LIU Bi-jin2,LIANG Shu-xiu3,SUN Zhao-chen3
(1 Ocean College,Zhejiang University,Zhoushan316021,China;2 Fujian Marine Forcasts, Fuzhou 350003,China;3 State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,Dalian 116024,China)

When interactions between water waves and offshore structures are dealt with,several big challenges have to be faced:distorted free surface,large-amplitude body motions and violent multiphase interactions.A numerical model is developed by using a Constrained Interpolation Profile(CIP)-based method, which is applicable of simulating free surface flow including wave breaking and overturing.The numerical simulation is performed through a CIP-based model with the CIP method adopted both as the base flow solver and the free surface capturing method.The numerical model is applied to a number of distorted free surface flow problems including dam breaking,dam breaking with an obstacle and extreme wave's impact on an offshore structure.The computational results are consistent with those obtained in other studies.

CIP method;free surface flow;high-order difference method;extreme wave; wave-body interaction

O352 O411.3

：Adoi:10.3969/j.issn.1007-7294.2016.04.002

1007-7294（2016）04-0393-10

2015-12-22

国家自然科学基金面上项目（51479175）；浙江省杰出青年科学基金（LR16E090002）

赵西增（1979-），男，博士，副教授，E-mail:xizengzhao@zju.edu.cn；梁书秀（1972-），女，博士，副教授，E-mail:sxliang@dlut.edu.cn。