深水环境下粘弹性复合材料夹层结构蠕变特性研究

杨 坤，吴 梵，邱家波

（1海军装备研究院舰船论证研究所，北京100161；2海军工程大学舰艇工程系，武汉430033；3海军潜艇学院防险救生系，山东青岛266042）

深水环境下粘弹性复合材料夹层结构蠕变特性研究

杨 坤1，吴 梵2，邱家波3

（1海军装备研究院舰船论证研究所，北京100161；2海军工程大学舰艇工程系，武汉430033；3海军潜艇学院防险救生系，山东青岛266042）

文章结合单轴压缩蠕变试验和粘弹性材料广义Maxwell建模理论得到吸声和浮体两种粘弹性填充材料的松弛模量Prony级数系数，开展了深水环境下粘弹性复合材料夹层结构蠕变特性试验，并将之与仿真研究结果进行对比，得到如下结论：复合材料夹层结构长时蠕变初期，芯材蠕变较表层复合材料占主导地位；随着时间增加，表层复合材料基体的粘弹性特性所表现出的蠕变和松弛现象交织出现，表层应变出现波动；芯材蠕变对复合材料夹层结构长时蠕变变形的贡献约为60%。

复合材料；夹层结构；粘弹性；深水环境；蠕变特性

0 引 言

复合材料因其具备耐腐蚀，轻质高强、高阻尼等特点，近年来在船舶工程领域应用非常广泛，随着结构力学性能优异的三层（夹层）或多层复合材料结构形式的出现以及各种轻质高强、吸声和减振功能型高分子材料不断研制成功，使得复合材料在船舶结构上的应用逐步向承载/功能型发展。为实现潜艇的减振降噪，复合材料夹层结构采用粘弹性芯材填充设计，由于填充芯材和纤维增强复合材料表层基体相的粘弹特性，将使得潜艇复合材料结构在长期深水环境中产生蠕变变形，进而影响结构变形、强度以及振动特性。复合材料结构蠕变特性的研究内容包括：纤维增强复合材料和粘弹性填充芯材的蠕变性能表征；材料粘弹性蠕变模型研究；组合结构蠕变特性计算模型的建立等。目前，已有不少文献对粘弹性材料开展理论建模及试验研究工作，纤维增强复合材料蠕变特性的研究主要分为试验研究[1-2]和微观力学模型研究[3]，针对复合材料夹层结构的蠕变问题，不少学者开展了解析理论研究，Ali[4]近似求解了较厚铺层复合材料结构非线性蠕变响应。Allam[5]分别考虑芯层或各向异性表层的粘弹性特性，求解了四边简支复合材料夹层板的准静态响应。Hamed[6]对不同材料组分采用不同的本构关系，利用叠加原理建立了复合材料层-粘接层-混凝土层结构的蠕变特性分析模型。针对复合材料复杂夹层结构的蠕变问题，有限元方法是一种有效的求解方法，Kim[7]提出了多级建模方法，讨论了复合材料夹层结构各组分材料对结构蠕变响应的影响。Beiss[8]采用Abaqus子程序对三维夹层结构高温条件下的蠕变特性进行了仿真研究。Morcous[9]针对纤维增强聚合物蜂窝夹层板的静力学特性，蠕变特性以及损伤特性开展了试验研究。本文针对深水中复合材料粘弹性夹层结构的蠕变问题，首先对其两种填充粘弹性材料开展蠕变试验研究，结合粘弹性材料广义Maxwel建模理论，得到了两种材料的松弛模量Prony级数系数，再采用Abaqus开展复合材料粘弹性夹层结构蠕变特性仿真计算，并与结构模型蠕变试验结果进行对比，研究结果对复合材料粘弹性夹层结构在深水环境中的应用具有借鉴意义。

1 粘弹性材料本构关系

1.1 广义Maxwell模型

模型理论能够比较直观地描述了粘弹性材料的力学行为，本文采用N个Maxwell单元组成（见图1）的广义Maxwell模型描述填充材料的粘弹性行为，由n对弹性元件和阻尼元件并联而成，其本构关系满足下列关系：

广义Maxwell模型的蠕变柔量定义为[10]：

图1 广义Maxwell模型示意图Fig.1 Generalized Maxwell model diagram

其中：L-1表示Laplace逆变换，Pk，qk为与弹性元件和阻尼元件参数相关的粘弹性材料的模型参数。

假设填充芯材为均质粘弹性材料，采用线性蠕变本构模型描述，其应变与时间关系为：

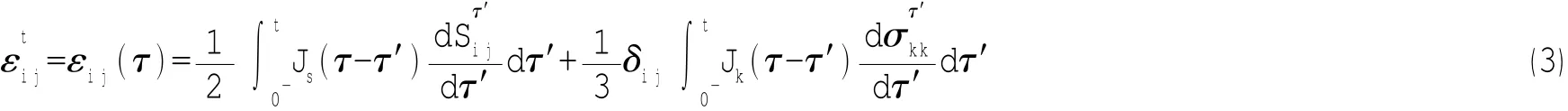
其中：Js（t）为剪切柔量，Jk（t）为体积柔量。为应力偏量和体积应力。τ′代表前一时刻，τ代表当前时刻。

1.2 松弛模量Prony级数系数的计算

为了简化结构粘弹性响应的复杂性，假设芯材泊松比与时间无关，在此假设条件下，芯材剪切蠕变柔量和体积蠕变柔量与单轴拉压蠕变柔量的关系为[7]：

其中：ν为泊松比，下标s表示剪切，k表示体积，J（t）为单轴拉压蠕变柔量，将其表达为无量纲剪切蠕变柔量js（t）和无量纲体积蠕变柔量jk（t）：

其中：G0为瞬时剪切模量，K0为瞬时体积模量。无量纲剪切蠕变柔量与无量纲剪切松弛模量，无量纲体积蠕变柔量和无量纲体积松弛模量之间的关系为[11]：

复杂结构粘弹性问题的数值计算通常采用符合广义Maxwell模型松弛模量形式的Prony级数表达：

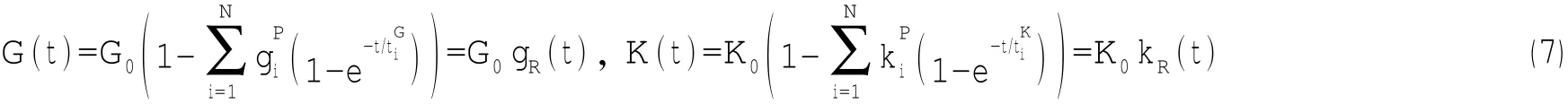
其中：G（t）为剪切松弛模量，K（t）为体积松弛模量，gR（t）为无量纲剪切松弛模量，kR（t）为无量纲体积松弛模量。上述运算过程可知由材料单轴蠕变试验数据得到其松弛模量Prony系数。

2 材料单轴压缩蠕变特性试验

针对复合材料夹层结构两种不同填充芯材开展载荷为3 MPa和5 MPa作用下的材料单轴蠕变试验，其蠕变曲线如图1所示，将不同载荷下材料的蠕变曲线转化为无量纲蠕变柔量，如图2所示，以判断两种材料是否属于线性粘弹性材料。

图2 填充芯材蠕变曲线Fig.2 Core filling material creep curves

图3 不同应力水平下材料的无量纲蠕变柔量曲线Fig.3 Dimensionless creep compliance curves of material under different stress level

由于材料本身的蠕变稳定状态分段特性，浮体材料蠕变曲线出现了阶梯跳跃，但从整体来看，吸声和浮体材料在两种不同应力水平下的无量纲蠕变柔量曲线基本重合，因此认为两者均为线性粘弹性材料，其蠕变特性与应力水平无关。

假设填充材料体积应变为弹性，对结构蠕变没有影响[7]，而剪切应变呈流变性，采用非线性最小二乘法将两种填充材料的无量纲蠕变柔量进行拟合，拟合平均均方根容差为0.001，拟合结果见图3，材料无量纲松弛模量Prony级数系数见表1。

图4 无量纲蠕变柔量试验曲线及拟合结果Fig.4 Dimensionless creep compliance test curves and the fitting result

表1 松弛模量Prony级数拟合系数Tab.1 Fitting coefficients of the relaxation modulus Prony series

3 复合材料夹层结构蠕变特性试验及仿真结果

3.1 试验及仿真过程

图5 应变测试现场Fig.5 Strain test scene

图6 悬臂梁位移测量装置Fig.6 Cantilever beam displacement measuring device

针对复合材料夹层结构开展蠕变特性试验和仿真研究，结构模型和应变测点布置见图4，位移测试装置见图5，试验模型外表面呈曲面，上下表层采用12 mm正交铺层玻璃纤维增强复合材料，内贴覆25 mm吸声芯材，最内层填充浮体材料，内部十字骨架及四周外板采用16 mm钢材。试验在压力桶内进行，测点布置和结构尺寸如图6所示，图中“ ”表示应变片测点，“●”表示位移测点。蠕变试验前进行多次加压（压力4.5 MPa）和泄压循环过程，直至相邻两次位移测量数据相同。为模拟270 m水深环境载荷，蠕变试验压力2.7 MPa，间隔0.5～2小时记录2天时间内测点位移和应变。利用ABAQUS开展结构蠕变仿真计算，夹层板板格有限元模型如图7所示，模型采用14 868个S4R单元，242 916个C3D8R单元，节点总数274 554个。施加均布载荷2.7 MPa。以Prony级数系数方式输入两种芯材的粘弹性参数，忽略表层基体粘弹性，纤维增强复合材料和钢质材料采用线弹性建模。

图7 测点布置图Fig.7 Measuring point layout

3.2 结果讨论

图8给出了位移测点试验及计算值随时间的变化曲线，同时给出了外载荷随时间的变化曲线，如图9所示。由图可知，计算蠕变曲线与实验值基本趋势一致；在初始阶段，试验模型完成瞬态弹性变形的时间较计算时间慢；0-20 000 s（5.5小时）时间段内，填充芯材蠕变占主导，结构位移计算值和试验值较为接近。随着时间的增加，计算值逐渐小于试验值，且相差呈增大趋势。原因分析：考虑到有限元计算规模，忽略复合材料表层基体粘弹性，未对其进行微观建模。对比试验和仿真结果的后期蠕变曲线可知，随着时间的增加，复合材料表层的粘弹性行为将更为明显。历经151 413 s（42小时）后，板格中心最大蠕变变形为0.747 mm（参考载荷波动情况，取倒数第二个时间的测量值），计算值为0.679 mm，以瞬态弹性变形值0.559为基准，得到结构总的蠕变变形为0.188 mm，计算值为0.120 mm；由此得到芯材蠕变对结构蠕变的贡献为63.8%。

图8 有限元计算模型Fig.8 Finite element calculation model

图10给出了表层复合材料应变测点测量结果。由图可知，结构应变在经历瞬态加载增大后，在0-20 000 s左右的时间段中将逐渐减小，由蠕变位移结果可知，在该阶段，表层复合材料蠕变变形较小，由于填充芯材产生蠕变变形，理论上夹层结构位移协调使得表层复合材料产生弹性变形，使得应变增大，但由于基体产生了应力松弛等复杂的粘弹性响应，导致测得应变测量结果逐渐减小。之后，由于表层基体交替蠕变和松弛，其应变曲线呈现不规律波动，这也是考虑表层建模的复合材料夹层结构长时力学特性分析的难度所在。

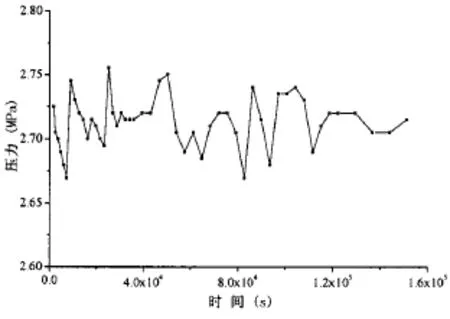
图10 压力载荷随时间变化曲线Fig.10 Pressure load curve at various time

图11 应变测点应变随时间的变化Fig.11 Strain measuring point strain at various time

4 结 论

本文通过材料蠕变试验和理论计算得到了两种粘弹性材料的松弛模量Prony级数系数，并将之应用于复合材料夹层结构蠕变特性仿真研究，对比复合材料夹层结构蠕变试验结果，得到如下结论：（1）芯材蠕变对粘弹性复合材料夹层结构蠕变变形的贡献为60%左右；（2）复合材料夹层结构在深水环境中长时蠕变初期，芯材蠕变占主导；（3）随着时间逐渐增加，表层复合材料基体的粘弹性特性所表现出的蠕变和松弛现象交织出现，表层应变出现波动。

[1]Tanmzs V,Andersons J,Aniskebich K.Creep and damage accumulation in orthotropic composites under cyclic loading[J]. Mechanics of Composite Materials,1998,34(4):321-330.

[2]Li Yiluen,Shen Mingyuan,Chen Weijen.Tensile creep study and mechanical properties of carbon fiber nano-composites [J].Journal of Polymer Research,2012,19:9893-9899.

[3]Yue Z F.Statistic modeling of the creep behavior of metal matrix composites bansed on finite element analysis[J].Applied Mathematics and Mechanics,2002,23(4):421-435.

[4]Ali R H,Muliana A.A micro-to-meso sublaminate model for the viscoelastic analysis of thick-section multi-layered Frp composite structures[J].Mechanics of Time Dependent Materials,2008,12(1):69-93.

[5]Allam M N M,Zenkour A M,Mekawy H F El.Bending response of inhomogeneous fiber-reinforced viscoelastic sandwich plates[J].Acta Mechanica,2010,209(3-4):231-248.

[6]Hamed E,Bradford M A.Creep in concrete beams strengthened with composite materials[J].European Journal of Mechanics A/Solids,2010,29(6):951-965.

[7]Kim J S,Arronche L,Farrugia A.Multi-scale modeling of time-dependent response of smart sandwich constructions[J]. Composite Structures,2011,93(9):2196-2207.

[8]Beiss P,Magd E El,Stuhrmann Jan.Characterization and simulation of the creep behavior of sandwich structures for cooling thermally highly loaded steam turbine components[J].Materials Science and Engineering A,2009,510-511(15):420-424.

[9]Morcous G,Cho Yong,Safty A El.Structural behavior of Frp sandwich panels for bridge decks[J].KSCE Journal of Civil Engineering,2010,14(6):879-888.

[10]陈静云,周长红,王哲人.沥青混合料蠕变试验数据的处理与粘弹性计算[J].东南大学学报（自然科学版）,2007,37 (6):1091-1095. Chen Jingyun,Zhou Changhong,Wang Zheren.Data processing and viscoelastic computation for creep test of asphalt mixture[J].Journal of Southeast University(Natural Science Edition),2007,37(6):1091-1095.

[11]杨挺青.粘弹性力学[M].武汉:华中科技大学出版社,1990.

Creep characteristics analysis of viscoelastic composite sandwich strcuture under static pressure of deep water environment

YANG Kun1,WU Fan2,QIU Jia-bo3
(1 Institute of Naval Vessels,Naval Academy of Armament,Beijing 100161,China;2 Dept.of Naval Architecture Engineering,Naval Univ.of Engineering,Wuhan 430033,China;3 Dept.of Rescue and Salvage,Naval Submarine Academy,Qingdao 266042,China)

Combined with the uniaxial compression creep test and viscoelastic material modeling theory of generalized Maxwell,the coefficients of relaxation modulus Prony series of absorption and floating viscoelastic filler material were obtianed.The creep charateristic experiment of viscoelastic composite sandwich structure under water was carried out,and the results were compared with the simulation research.The results show that at the long-term creep stage of composite materials sandwich structure,the core material has a dominant presence compare with composite material;with the increase of time,the creep and relaxation phenomena exhibited by viscoelastic properties of the surface composite matrix appear alternately, the surface strain fluctuates;on long-term creep deformation of composite sandwich structure,the core material contributes about 60%.

composite;sandwich;viscoelastic;deep water environment;creep characteristic

TB564

：Adoi:10.3969/j.issn.1007-7294.2016.04.015

1007-7294（2016）04-0508-06

2015-11-24

杨 坤（1986-），男，博士，工程师，E-mail:yangkuntuo@163.com；吴 梵（1962-），男，教授，博士生导师。