基于一种固体区域迭代算法的圆柱涡激振动数值计算

章大海，石凡奇，王 君，郝木明

（中国石油大学（华东）化学工程学院，山东青岛266580）

基于一种固体区域迭代算法的圆柱涡激振动数值计算

章大海，石凡奇，王 君，郝木明

（中国石油大学（华东）化学工程学院，山东青岛266580）

利用Fluent平台的用户自定义程序（UDF）以及动网格模型，实现了圆柱运动方程的一种迭代求解算法，分别对层流、湍流状态下，弹性支承圆柱体在一定约化速度下的涡激响应进行了数值模拟，探讨了不同阻尼比对涡激响应的影响。结果表明：采用该迭代求解算法对弹性支承圆柱涡激振动的预测结果较为合理；随着阻尼比的逐渐增加，初始支振幅、升阻力系数时程曲线将由多频率拍振，最终变为单一频率主导的振动，且涡激振幅逐渐减小；除了质量-阻尼比联合参数m*ζ外，阻尼比ζ本身也应作为一个重要的涡激影响参数单独进行考量。

涡激振动；流固耦合；阻尼比；数值模拟

0 引 言

流体流经管道时在管体两侧形成的交替涡脱会诱发管道的周期性振动，而管道的振动又会扰乱流场涡的脱落，这种流体-固体耦合作用的现象称为“涡激振动”（Vortex-induced Vibration，VIV）。长输管道，特别是海洋立管的涡激振动是当今工业界研究的热点和难点。立管涡激振动预测水平的提高，能直接减少海洋平台建造成本。加强涡激振动的研究对石油工业的意义不言而喻。

由于立管现场全比例实验极其耗费资源，研究者主要从数值模拟和缩比尺实验进行涡激振动研究。相关综述可参考Sarpkaya[1]，Williamson[2-3]，Gabbai[4]等。最早且最著名的实验研究是Feng[5]在英属哥伦比亚大学风洞所作的自激振动实验。Feng对质量比m*=248的圆柱体在横向运动的响应进行了研究。其中横向振幅表现出两个响应分支，初始分支和下端分支，振幅幅值为0.6D。以Williamson为首的实验小组[6-9]对低质量比m*=O（10）量级的振动系统进行了一系列的实验研究，其目的在于探究涡激振动的内在机理，并为涡激振动的锁定、迟滞现象找到了合理的解释。Willamson小组的实验结果表明：（1）振动幅值由质量-阻尼联合参数控制。当质量-阻尼组合参数m*ζ较大时，呈现初始支和下支两支响应，而该参数较小时，呈现三支响应（出现了上支）；（2）旋涡脱落在初始支为2S模态，在上支和下支为2P模态，初始支与上支之间存在“迟滞性过渡”，而上支与下支之间为“间隙性转换”；（3）当m*ζ为定值时，锁定区域的速度范围随m*的增大而减小。Zhao[10]将弹性支撑圆柱体自激振动得到的振动曲线作为受迫振动的输入数据，结果表明，二者可得到几乎完全相同的流体力信息和尾涡模式，更为直观地显现了两种振动实验的联系。

受限于人们对湍流的有限认知以及计算机技术发展水平，至今仍不能对涡激振动进行精确模拟。目前，弹性支撑圆柱体的涡激振动的CFD模拟主要有以下途径：基于有限体积法的直接数值模拟（DNS）、大涡模拟（LES）、雷诺时均方法（RANS）、以及最近提出的离散涡方法（DVM）和格子Boltzmann方法（LBM）。林琳等[11-12]利用RANS方法比较了固定圆柱绕流外流场与振动圆柱外流场的区别，认为SST k-ω模型的模拟结果优于RNG k-ε模型；何长江[13]采用动网格的动态铺层模型和滑移网格模型以及用户自定义程序，将计算结构响应的Newmark代码嵌入FLUENT软件，建立了二维圆柱横流向涡激振动的计算模型。潘志远[14]利用RANS方法结合一定的网格策略模拟了水流当中圆柱体横向自激振动与受迫振动。黄智勇[15]在其研究基础上模拟了圆柱的二自由度自激振动。研究表明，在质量比低于3.5时，两自由度圆柱的横向振幅比单自由度情况大。董婧等[16]采用离散涡方法和四阶Runge-Kutta法计算了低雷诺数条件下圆柱体的涡激振动，分析了决定圆柱振动的影响参数及尾涡结构与气动力的关系，观察到“拍”和“相位开关”等现象。陶实[17]应用格子Boltzmann方法对弹性支承圆柱涡激振动进行了数值模拟，研究Sg数、质量比、频率比对涡激响应的影响，结果表明质量比对振幅的抑制效果最显著；且频率比足够大时，会呈现“8”字型运动轨迹。

以上模拟方法各有优势，能较为准确地捕捉涡激振幅和频率响应。但在固体区域控制方程的处理均无一例外采用Runge-Kutta法或Newmark方法。本文利用Fluent平台内嵌的用户自定义程序（User-defined Functions,UDF）以及动网格模型，实现了圆柱运动方程的一种迭代求解算法，研究了弹性支承圆柱体在一定约化速度范围内的涡激响应，以及不同阻尼比对涡激响应的影响。计算结果表明，与现有模拟方法相比，本文采用的迭代求解算法也能对弹性支承圆柱涡激振动做出相同精度的预测；随着阻尼比的逐渐增加，初始支振幅、升阻力系数时程将由多频率拍振，最终演变为单一频率主导的振动，且涡激振幅逐渐减小。因而本文认为，除了Williamson小组[6-9]所建议的质量-阻尼比联合参数m*ζ外，阻尼比ζ本身也应作为一个重要的涡激影响参数单独进行考量。

1 计算模型

1.1 几何模型

弹性支承圆柱振动系统简化为图1所示的物理模型。整个计算域取为如图1所示的长方形区域。圆柱直径D，圆柱中心距离上，下及左边界的距离为10D，距离右边为20D，以保证充分泻涡；总网格数约2.0×104个，且为保证圆柱附近流场计算的精度，紧贴圆柱布置随圆柱运动的结构化网格，厚度约1D，如图2所示。其中，圆管表面第一层网格的高度为0.01D。流体密度ρ=1 000 kg/m3，粘度ν=1.01× 10-6m2/s。湍流情况采用SST k-ω模型，网格左端为速度入口，右端为压力出口；上下边界为对称边界条件。由于涡激振动涉及到计算网格的运动，利用动网格的重构和弹簧光顺方法，实现网格的运动和更新。

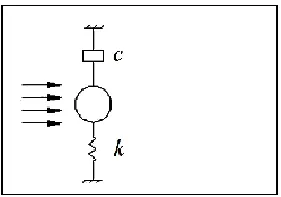
图1 几何模型示意图Fig.1 Model sheme of elastically mounted cylinder

图2 圆柱附近网格Fig.2 Grid near cylinder

1.2 结构动力学方程

对于图1中的单自由度（single degree of freedom,sdof）弹簧-质量-阻尼系统，其控制方程为：

其中：y，m，c，k分别为圆柱位移，圆柱质量，结构阻尼系数和系统刚度系数。FL（t）为系统所受横向流体力

进行无量纲化后可得

1.3 计算流程

基于Fluent平台，利用其用户自定义函数（UDF）实现固体和流体控制方程的耦合。首先将（3）式简化为如下形式：

根据（7）、（8）式利用迭代思想就可进行结构方程求解程序的编写。编写代码时，给定初始速度为0 m/s，在每时间步只需提取流体力FL，就可对结构运动方程予以求解。基于Fluent的UDF内嵌机制，将求解代码嵌入Fluent，实现流体与结构控制方程的耦合；同时利用动网格的弹簧光顺（spring-based smoothing）及局部重构（local remeshing）模型对网格进行更新，即可对圆柱涡激振动问题进行时域范围求解。

2 弹性支承圆柱的涡激响应

考虑层流和湍流两种情况下弹性支承圆柱的涡激响应。为与Williamson小组的文献保持一致，图3～8采用约化速度表达式U*=U∞/fnwD进行处理。层流情况模型直径D=0.01 m，质量比m*=2.8，水中的固有频率fnw=0.35 Hz，约化速度U*=3～16，对应雷诺数范围为100～600。湍流情况D=0.038 1 m，质量比m*=8.6，fnw=0.4 Hz，约化速度U*=3～12，对应雷诺数范围为1 800～8 000，计算结果如图3～6所示。

图3给出了本文的计算结果与实验数据的对比。湍流情况下，本文得出的最大振幅出现在U*=5.6处，最大振幅值约为A/D=0.52，振幅变化趋势与Govardhan[7]的实验结果相符，但本文模拟出初始支的最大振幅比实验结果偏小。产生本文结果的重要原因可能是本文采用的弱耦合算法。弱耦合算法在一个时间步内分开来求解流场和固体区域的控制方程，流体、固体区域物理量（流体力、固体位移）通过流固交界面插值计算来进行交换。因此，在耦合界面上的动量是不完全守恒的[19]，这可能是造成本文算例振幅偏大的最重要的因素。值得注意的是，在相同约化速度下，层流状态和湍流状态下的涡激振幅响应有明显差别。图3清楚地表明，湍流状态下的振幅响应比层流状态大，且锁定区域对应的无量纲速度范围也更大。因此，单独用约化速度不能作为涡激响应的衡量标准，还应加上标明流场本身性质的雷诺数。图4给出了约化速度U*=5.6时，对应锁定状态下流体力系数与圆柱振幅时程。可以看出：在锁定现象发生时，圆柱的升力系数曲线和圆柱振幅曲线的波峰、波谷对应，二者相位一致，表明流体向圆柱输送能量，出现类似共振的“锁定现象”。阻力系数频率约为升力系数两倍。以上结论均与实验结论一致，因而本文采用的迭代算法是有效的。

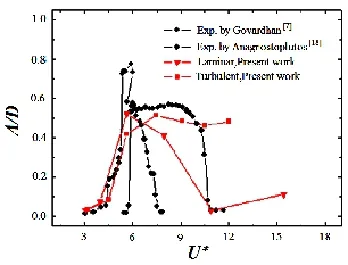
图3 振幅曲线[7，18]Fig.3 Amplitude response as a function of reduced velocity

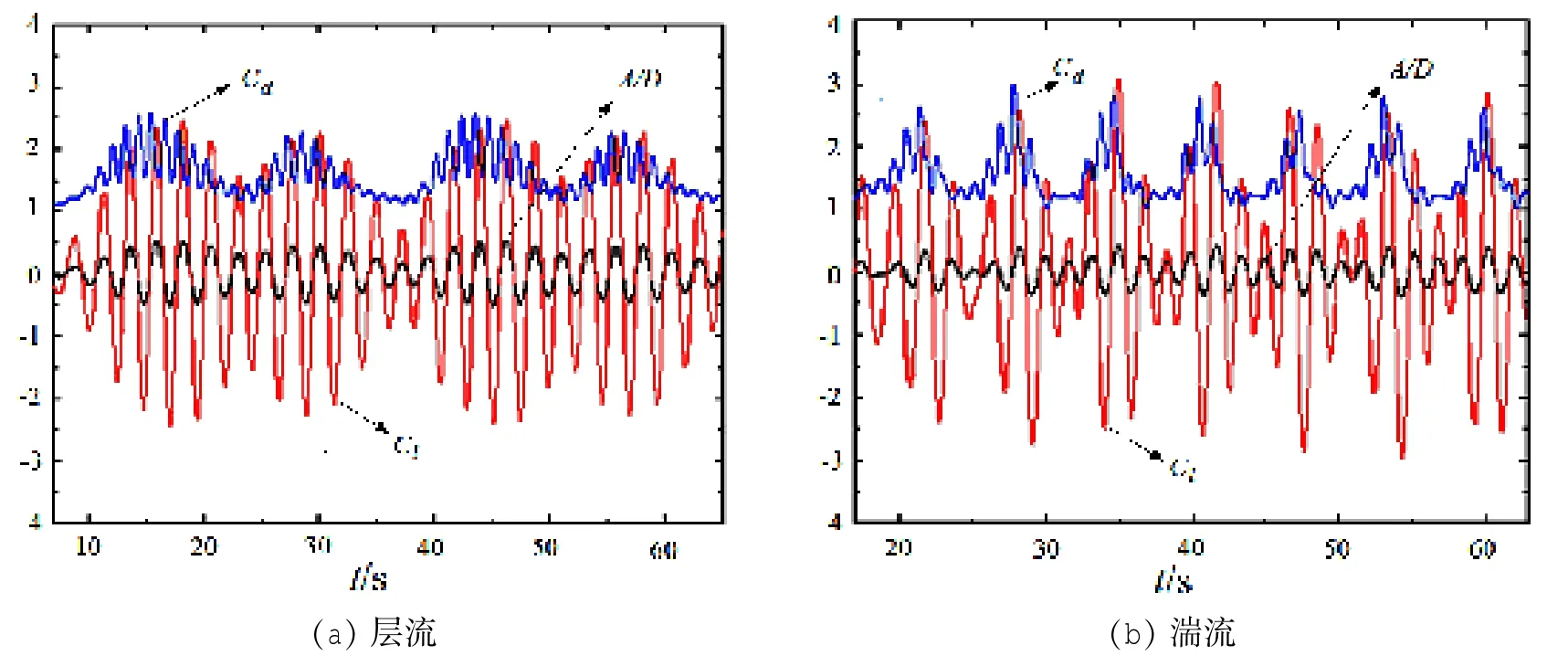
图4 U*=5.6，振幅及流体力系数曲线Fig.4 Time traces of cylinder amplitude and fluid forces,U*=5.6

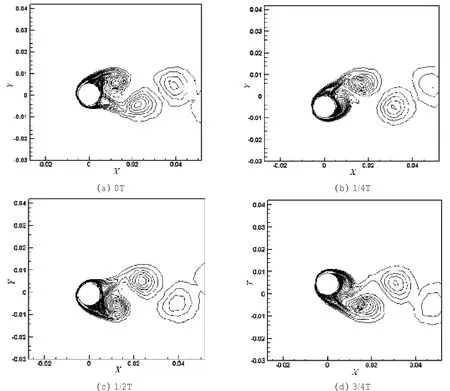
图5 层流状态下圆柱体单个振动周期内流场涡量图，U*=5.6Fig.5 Vorticity magnitude contours within a vortex shedding period,laminar flow,U*=5.6

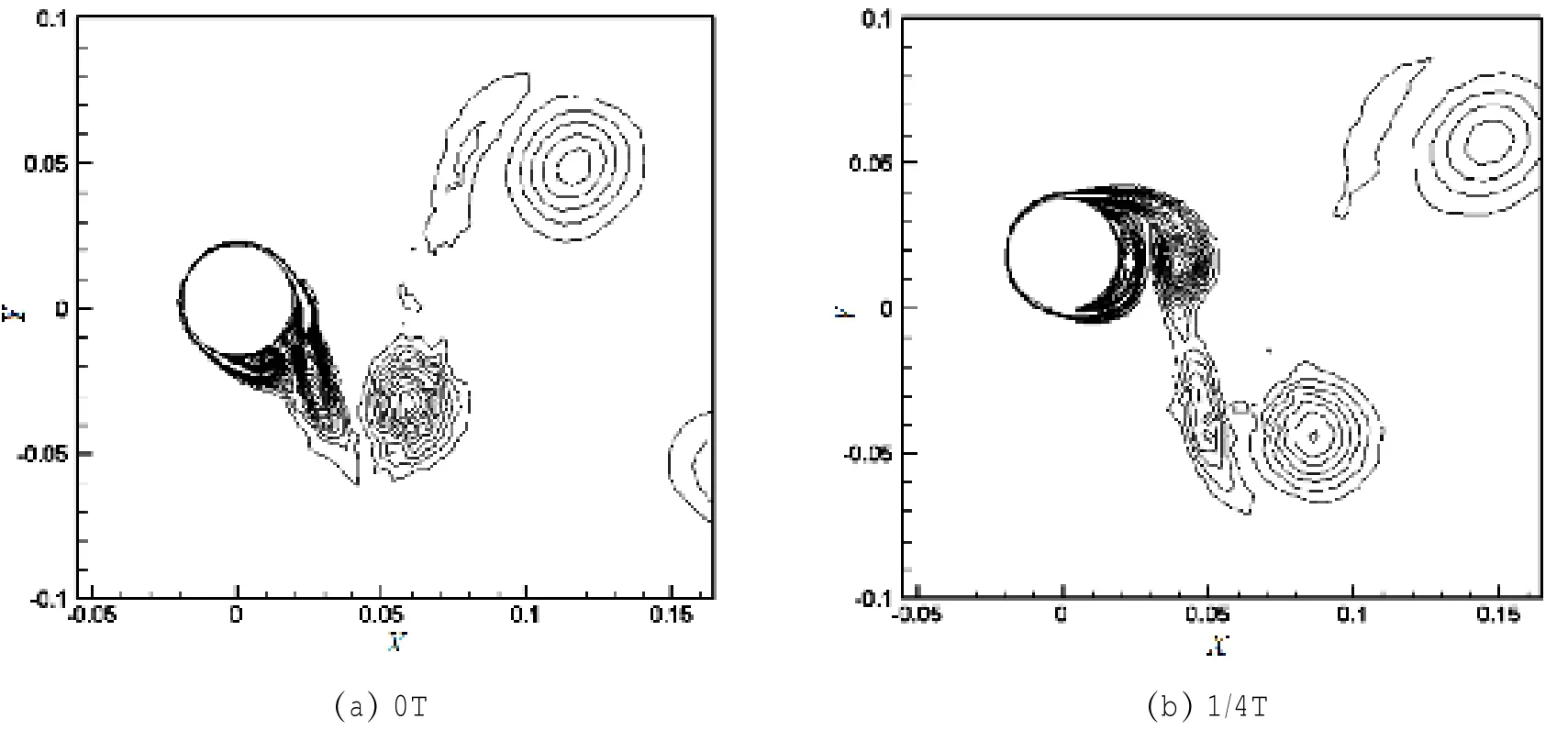
图6 湍流状态下圆柱体单个振动周期内流场涡量图，U*=7.5Fig.6 Vorticity magnitude contours within a vortex shedding period,turbulent flow,U*=7.5

本文层流状态下的模拟捕捉到2S的泻涡模式，如图5所示；图6给出的湍流状态下（对应U*=7.5）圆柱一个振动周期内涡量等值线图清晰地捕捉到了2P泻涡模式。Williamson小组[5-9]实验结果表明：低质量比弹性支撑圆柱涡激振动中与振动响应初始分支对应的尾涡为2S模式，而与上端分支和下端分支对应的尾涡则为2P模式。本文结果与之相符，这也验证了计算方法的有效性。

3 阻尼比对涡激响应的影响

研究层流和湍流情况下阻尼比对涡激响应的影响。层流、湍流工况均取涡激响应初始支，U*=5.6。采用阻尼比为ζ=0，4.6×10-3，9.2×10-3，9.2×10-2，其余实验参数与上节相同。模拟结果如图7～8所示。

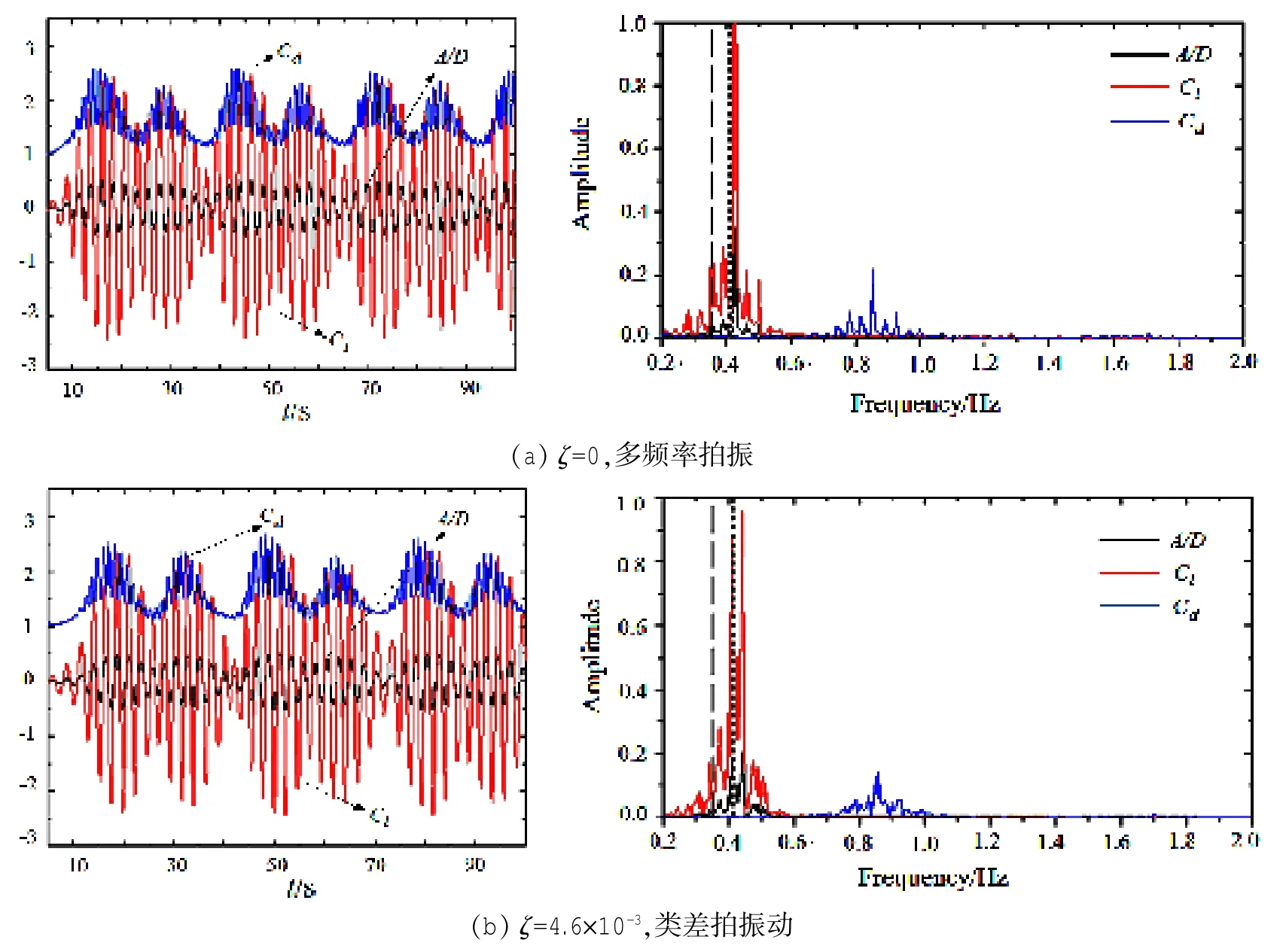
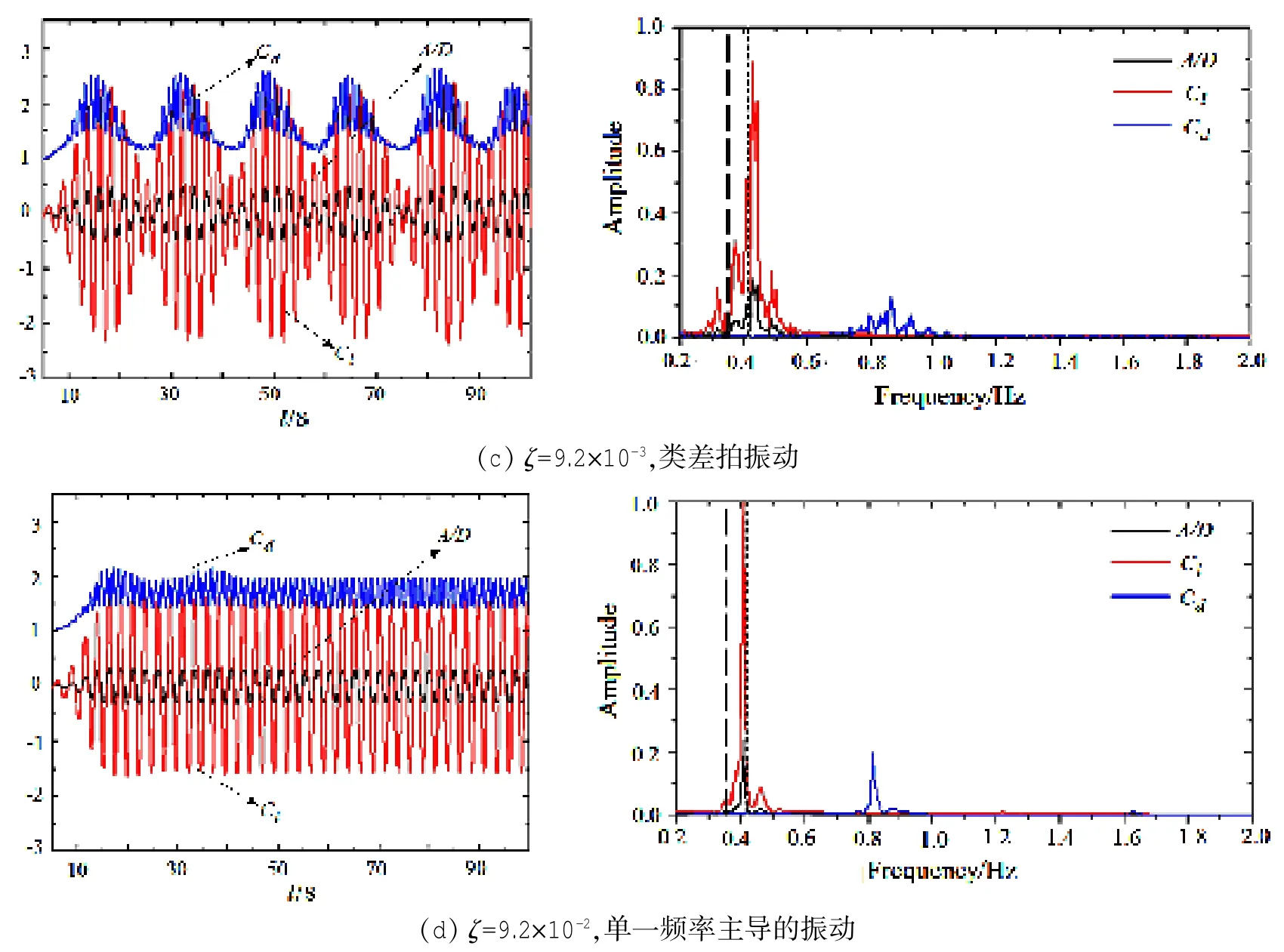
图7 层流情况下不同阻尼比圆柱的涡激响应时程及对应频谱。频谱图中两条虚线分别是系统在水中的自然频率fnw=0.35和空气中的自然频率fn=0.41Fig.7 Amplitude and fluid force response and corresponding spectrum under different damping ratios,laminar case. Dash lines indicate the natural frequencies of the system in water and air respectively

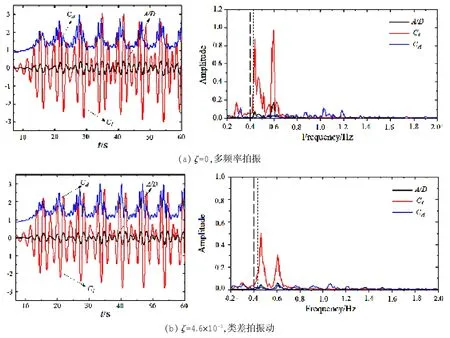
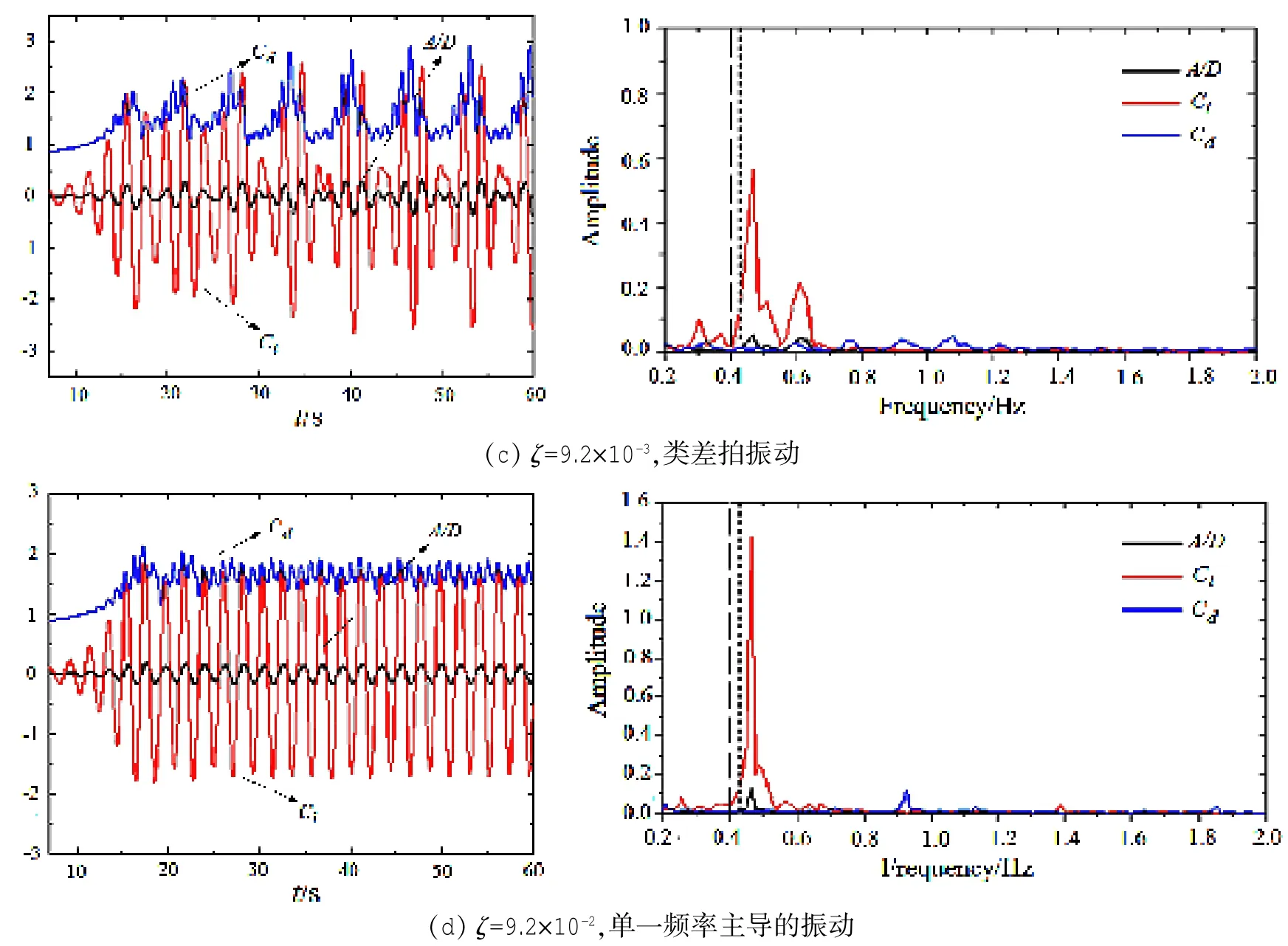
图8 湍流情况下不同阻尼比圆柱的涡激响应时程及对应频谱。频谱图中两条虚线分别是系统在水中的自然频率fnw=0.40和空气中的自然频率fn=0.42Fig.8 Amplitude and fluid force response and corresponding spectrum under different damping ratios,turbulent case. Dash lines indicate the natural frequencies of the system in water and air respectively

图7、图8表明，阻尼比对涡激响应有显著影响。在振动响应的初始支，层流情况下，阻尼比ζ=0时，升力系数、涡激振幅时程表现出多频率拍振现象，最大振幅在0.50左右；阻尼比ζ=4.6×10-3，9.2× 10-3时，振幅、升力时程表现出两个频率主导的类似差拍振动现象。升力系数和涡激振幅时程的频谱分析显示，ζ=4.6×10-3时，二者主要集中在fex=0.439、0.409两个频率振动，最大振幅约0.51；阻尼比ζ增大为9.2×10-3时，升力和振幅主要集中在频率fex=0.439、0.427振动，两频率相互靠近，最大振幅0.49；而当阻尼比继续增大到9.2×10-2时，升力系数和振幅集中在单一频率振动，最大振幅为0.30。湍流情况下的情况与此类似，随着阻尼比的增大，振动响应越来越明显地表现为靠近fnw的单频振动，频率远离fnw的振动成分逐渐消失。可以看出，随着阻尼比的逐渐增加，初始支的振幅、升阻力系数时程由多频率拍振，逐渐演变为两频率主导的类似差拍振动，最终变为单一频率主导的振动，且振幅逐渐减小。因而本文认为，除了Williamson小组[6-9]所建议的质量-阻尼比联合参数m*ζ外，阻尼比ζ本身也应作为一个重要的涡激影响参数单独进行考量。

4 结 语

本文跟踪了圆柱绕流现象的最近研究成果，利用Fluent平台内嵌的用户自定义程序（UDF）以及动网格模型，实现了圆柱运动方程的另一种迭代求解算法，研究了弹性支承圆柱体在一定约化速度范围内的涡激响应，以及不同阻尼比对涡激响应的影响。计算结果表明：

（1）与现有固体区域求解方法相比，本文采用的迭代求解算法也能对弹性支承圆柱涡激振动做出相同精度的预测；

（2）随着阻尼比的逐渐增加，涡激响应初始支振幅、升阻力系数时程将由多频率拍振，最终演变为单一频率主导的振动，且涡激振幅逐渐减小。因而本文认为，除了Williamson小组[6-9]所建议的质量-阻尼比联合参数m*ζ外，阻尼比ζ本身也应作为一个重要的涡激影响参数单独进行考量。

[1]Sarpkaya T.A critical review of the intrinsic nature of vortex-induced vibrations[J].Journal of Fluids and Structures,2004, 19(4):389-447.

[2]Williamson C H K,Govardhan R.Vortex-Induced Vibrations[J].Annual Review of Fluid Mechanics,2004,36(1):413-455.

[3]Williamson C H K,Govardhan R.Govardhan.A brief review of recent results in vortex-induced vibrations[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96(6-7):713-735.

[4]Gabbai R D,Benaroya H.An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J]. Journal of Sound and Vibration,2005,282(3-5):575-616.

[5]Feng C C.The measurement of vortex induced effects in flow past stationary and oscillating circular and dissection cylinders [D].Canada:University of British Columbia,1968.

[6]Morse T L,Williamson C H K.The effect of Reynolds number on the critical mass phenomenon in vortex-induced vibration[J].Physics of Fluids,2009,21(4):045105.

[7]Govardhan R,Williamson C H K.Modes of vortex formation and frequency response of a freely vibrating cylinder[J].Journal of Fluid Mechanics,2000,420:85-130.

[8]Morse T L,Williamson C H K.The effect of Reynolds number on the critical mass phenomenon in vortex-induced vibration[J].Phisics of Fluids,2009,21(045105):1-8

[9]Khalak A,Williamson C H K.Dynamics of a hydroelastic cylinder with very low mass and damping[J].Journal of Fluids and Structures,1996,10:455-472.

[10]Zhao J,Nemes A,Lo Jacono D,et al.Comparison of fluid forces and wake modes between free vibration and tracking motions of a circular cylinder[C]//18th Australian Fluid Mechanics Conference.Launceton,Australia,2012.

[11]林 琳,王言英.自激振动圆柱体湍流场及发展变化的研究[J].振动与冲击,2013,32(14):164-173. Lin Lin,Wang Yanying.Computation of a turbulence flow and its development around a self-induced vibrating circular cylinder[J].Journal of Vibration and Shock,2013,32(14):164-173.

[12]林 琳,王言英.不同湍流模型下圆柱涡激振动的计算比较[J].船舶力学,2013,17(10):1115-1125. Lin Lin,Wang Yanying.Comparison between different turbulence models on vortex induced vibration of circular cylinder [J].Journal of Ship Mechanics,2013,17(10):1115-1125.

[13]何长江,段忠东.二维圆柱涡激振动的数值模拟[J].海洋工程,2008,26(1):57-63. He Changjiang,Duan Zhongdong.Numerical simulation of vortex induced vibration on 2D circular cylinders[J].Ocean Engineering,2008,26(1):57-63.

[14]潘志远.海洋立管涡激振动机理与预报方法研究[D].上海:上海交通大学,2005. Pan Zhiyuan.Vortex induced vibration of marine riser and response prediction[D].Shanghai:Shanghai Jiao Tong University,2005.

[15]黄智勇,潘志远,崔维成.两向自由度低质量比圆柱体涡激振动的数值计算[J].船舶力学,2007,11(1):1-9. Huang Zhiyong,Pan Zhiyuan,Cui Weicheng.Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio[J].Journal of Ship Mechanics,2007,11(1):1-9.

[16]董 婧,宗 智,李章锐,等.两自由度运动圆柱绕流的离散涡方法模拟[J].船舶力学,2012,16(1-2):9-20. Dong Jing,Zong Zhi,Li Zhangrui,et al.Numerical simulation of flow around a cylinder of two degrees of freedom motion using the discrete vortex method[J].Journal of Ship Mechanics,2012,16(1-2):9-20.

[17]陶 实,周 力,宗 智.基于格子Boltzmann方法的圆柱两自由度涡激振动的研究[J].水动力学研究与进展,2013, 28(2):167-175. Tao Shi,Zhou Li,Zong Zhi.Vortex-induced vibration of circular cylinder with two degrees of freedom based on Lattice Boltzmann simulation[J].Chinese Journal of Hydrodynamics,2013,28(2):167-175.

[18]Anagnostoplutos P,Bearman P W.Response characteristics of a vortex-excited cylinder at low reynolds numbers[J].Journal of Fluids and Structures,1992,6:39-50.

[19]陈 锋,王春江,周 岱.流固耦合理论与算法评述[J].空间结构,2012,18(4):55-63. Chen Feng,Wang Chunjiang,Zhou Dai.Review of theory and numerical methods of fluid-structure interaction[J].Spatial Structures,2012,18(4):55-63.

Numerical simulation of VIV of a cylinder using an iteration method in calculating cylinder motion

ZHANG Da-hai,SHI Fan-qi,WANG Jun,HAO Mu-ming
(College of Chemical Engineering,China University of Petroleum,Qingdao 266580,China)

An iteration method is adopted in numerical simulation,to solve the motion of an elastically mounted cylinder of VIV based on Fluent UDF codes.Cases of laminar flow and turbulent flow are conducted respectively,within a range of reduced velocity,and cases with different damping ratios are analyzed. Comparison with experimental data verifies the validity of the method.The resuts show that the lift coefficient and the amplitude of the cylinder will transform from multi-frequency oscillation to single frequency oscillation,and the maximum amplitude will decrease as damping ratio increases.Therefore damping ratio ζ should be regarded as an independent parameter in addition to the well known mass-damping parameter m*ζ.

Vortex-Induced Vibration;solid-fluid interaction;damping ratio;numerical simulation

O237

：Adoi:10.3969/j.issn.1007-7294.2016.04.006

1007-7294（2016）04-0430-09

2015-07-13

山东省自然科学基金项目（ZR2012EEQ011）

章大海（1978-），男，博士，副教授，E-mail:dhzhang@upc.edu.cn；石凡奇（1989-），男，硕士研究生，E-mail:andy20110920@hotmail.com。