振荡来流下柔性立管涡激振动响应特性试验研究

王俊高，付世晓，许玉旺，宋磊建

（上海交通大学海洋工程国家重点实验室，上海200240）

振荡来流下柔性立管涡激振动响应特性试验研究

王俊高，付世晓，许玉旺，宋磊建

（上海交通大学海洋工程国家重点实验室，上海200240）

在顶部浮体的带动下，悬链线立管的动力响应会诱发其周围产生相对来流，而这种振荡来流将激励立管悬垂段产生“间歇性”的涡激振动。文章在海洋工程水池中对不同最大约化速度URmax、KC数组合下的振荡来流作用下的柔性立管开展模型试验研究，利用光纤应变片测量模型的涡激振动响应。结合模态分析与小波变换对试验数据进行分析，讨论并总结了最大约化速度URmax以及KC数对涡激振动位移幅值响应特性的影响规律。文中进一步分析发现振荡来流下的涡激振动响应还存在“迟滞”及“高阶谐频”现象。

振荡来流；涡激振动；迟滞；高阶谐频

0 引 言

在复杂的海洋环境载荷作用下，深海柔性立管的涡激振动呈现出多模态参与、随机性强等特点。因此，准确地预报立管在实际海洋环境中所受的载荷及动力响应一直是海洋工程领域中的重要课题。关于柔性立管涡激振动的预报方法，主要分为两种：基于强迫振荡试验的经验模型预报和模型试验。

比较有代表性的经验预报模型有Vandiver等[1]开发的SHEAR7和Larsen等[2]开发的VIVANA。经验预报模型基于强迫振荡试验得到的水动力系数，利用能量平衡迭代计算预报立管涡激振动。由于实际海洋环境与实验环境差异较大，这些方法给出的预报结果往往难以令人满意。

迄今为止，诸多学者开展了定常来流下柔性立管的涡激振动试验[3-16]。这些试验反映了高阶多模态响应、行波以及CF（Cross Flow）、IL（In Line）之间的耦合等涡激振动的复杂现象。这对于柔性立管涡激振动的认识及预报有着极大的推动。然而，这些试验考虑的均为定常来流（来流性质不随时间变化）。

真实海洋环境中，风、浪、流的作用会引起浮体产生复杂的运动响应。从而将带动连接于它们的立管、脐带缆等在水中往复运动，从而在管线与周围水质点之间形成相对振荡来流，一般用KC数来表示物体在水中相对运动的幅度，

其中：Am为振荡幅值，D为结构的截面直径。对于实际使用的钢悬链线立管，由于其几何形状的特殊性，使得KC数沿管长分布并不统一。并且不同激励频率的顶部浮体运动也必然使得立管动力响应频率并不固定。由此可见，找出振荡来流作用下涡激振动响应特性对其动力响应的准确预报是极其重要的。

近年，美国STRIDE项目中的一次针对钢悬链线立管动力响应的试验偶然发现了这种不是由背景来流导致，而是仅由顶部平台运动引发的“间歇性”的涡激振动[17]。Mark Chang[18]利用尾流振子模型和离散涡模型对平台垂荡引起的立管涡激振动进行了简单的预报计算，然而这种基于均匀来流下涡激振动的经验预报模型的准确性还没有得到试验的验证。Liao[19]提出用约化质量-阻尼系数Sg以及波传播参数nζ来分析立管在非定常来流下的涡激振动响应。他提出了针对立管动边界动力响应的算法，并分析了激励频率、立管固有频率、泄涡频率以及立管响应频率之间的相互关系，但没有通过相应的试验对其算法进行验证。MIT的Enrique[20]通过有限元软件计算了钢悬链线立管在顶部浮体带动下沿长度方向的最大速度、KC数及最大泄涡频率分布，并根据泄涡频率与固有频率之间的关系来判断涡激振动是否发生。同时他针对钢悬链线立管进行了室内模型试验，在静水中对立管施加顶部浮体运动，发现几种不同形式的钢悬链线式立管在平台运动诱发下均发生了涡激振动。但由于模型直径仅为5 mm，无法在其表面布置传感器测量运动响应，所以仅对模型顶部的反力进行频谱分析，这显然无法准确全面地反映钢悬链线立管本身（尤其是接近触地点的悬垂段）在振荡流作用下的涡激振动发生的规律；试验也没有给出定量的KC数与涡激振动响应之间的关系。

综上所述，目前的柔性立管的涡激振动研究主要着眼于定常来流。对于振荡来流下的涡激振动，学术界开展了一些理论和试验研究，但还没有得到振荡来流与悬链线立管涡激振动之间的作用规律，也没有针对这种涡激振动产生的根本原因-振荡来流，分析最大约化速度URmax、KC数与立管涡激振动间的关系。

本文从不同振荡来流参数（KC数、最大约化速度URmax）的角度进行了振荡来流下立管涡激振动响应特性试验研究，发现其明显区别于定常来流作用下的涡激振动。利用模态分析、小波分析对试验数据处理得到振荡来流下涡激振动的位移响应幅值、响应频率，并讨论总结了最大约化速度URmax、KC数对涡激振动响应特性的影响规律。同时还发现其存在“迟滞”现象及“高阶谐频”响应。这些通过试验结果反应出的涡激振动响应表现出很强的“时域特征”-其响应特性随时间（约化速度的增减）发生显著变化。因而，本文中分析总结的振荡来流下立管涡激振动响应特性将为未来发展新的涡激振动预报模型奠定理论基础，并提供一定的技术支撑。

1 试验描述

1.1 试验装置

试验在上海交通大学的海洋工程水池中进行，振荡试验装置安装在拖车底部，试验装置由两条水平轨道以及安装在水平轨道上的两条竖直导轨构成，其简图如图1所示。

模型端部安装示意图如图2所示：立管模型经端部夹紧装置与万向节一端相连，万向节另一端连接于固定在竖直轨道运动滑块上的三分力仪。模型两端布置三分力仪测量张力的实时变化。另外，振荡装置与模型连接处安装有两块绕流板以避免振荡装置的大幅运动扰动试验区域流场。

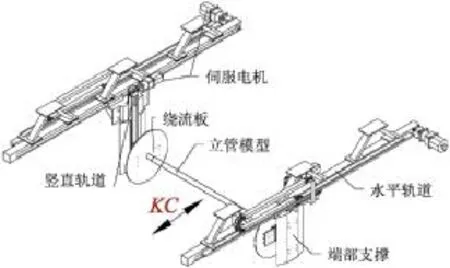
图1 试验装置示意简图Fig.1 Simplified sketch of the setup

图2 试验模型端部装置细节图Fig.2 Detailed view of the end condition

1.2 试验模型

试验模型的主要参数如表1所示。

根据试验模型在水中运动方式将其分为CF与IL两个方向布置四组光纤应变传感器，其布置方式如图3所示。从模型截面来看：a、c两条线关于模型中性层对称，为CF方向，沿其轴向方向均布7个应变测点；b、d属于IL方向，沿其轴向方向均布11个应变测点。各应变测点的具体位置如表2所示。

在试验数据采集时，运动机构速度信号、张力信号以及应变信号同步采集，采样频率为250 Hz。

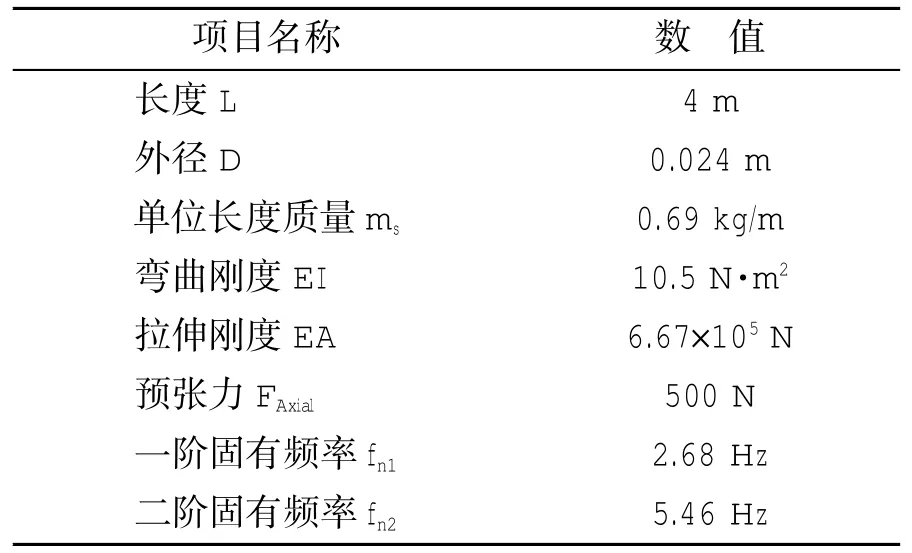
表1 模型物理参数Tab.1 Physical properties of the test cylinder

表2 光纤应变点位置Tab.2 Arrangement of the FBG strain sensors

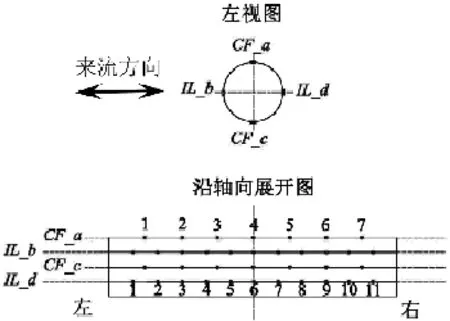
图3 光纤应变片布置示意图Fig.3 Instrumentation of the model

1.3 试验内容

试验针对最大约化速度URmax、KC数两个参数研究了柔性立管在振荡来流作用下的涡激振动响应特性。其中根据最大约化速度URmax将试验工况分为3大类，每组工况中KC数的范围为26-178。具体试验工况总结如表3所示。

试验开始时，水平轨道上的伺服电机带动模型以设定的振幅Am和振荡周期T在静水中进行水平简谐振荡。模型运动的振幅、速度可用公式表示如下：

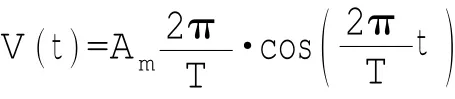
表3 试验工况Tab.3 Test cases

2 试验数据分析

2.1 涡激振动引起应变获取

试验过程中，模型两端施加500 N的预张力，模型的往复运动会使两端张力不断发生变化。这样，模型表面测得的应变就包括：预张力引起的初始拉伸应变、运动过程中张力变化引起的轴向应变和涡激力引起的弯曲应变。为了消除张力对弯曲应变的影响，将关于中性层对称的两测点的测量值相减再取平均值，可得到涡激振动引起的弯曲应变。因此，最终可以得到如（3）式所示的涡激振动引起的弯曲应变。

式中：εCF_a（t）和εCF_c（t）分别表示CF_a，CF_c两测点在试验中测得的应变时历；而εCF_VIV（t）表示消除了张力影响后的由涡激振动引起的弯曲应变时历。

2.2 模态分析

模态分析法基于线性模态叠加，可以将模型表面测得的应变信号结合结构的模态振型计算得到测点的位移。一般地，模型表面的位移可以表示为：

式中：pi（t）表示第i阶模态的位移权重，φi（x）表示模型的第i阶位移振型。

由于位移与曲率之间存在的空间二次导数关系，可以得到曲率κ（t,x）的表达式如下：

本文中的试验模型为张紧梁模型，其第i阶位移振型可以用正弦三角函数表示为：φi（x）=sin，则曲率振型。

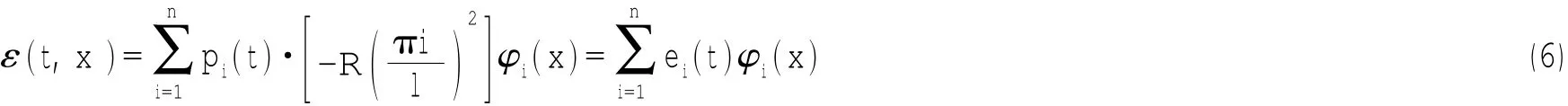
式中：ei（t）为第i阶应变模态权重。通过方程（4）、（5）和（6）就能建立起应变ε（t,x）与位移w（t,x）的关系。

2.3 时频小波分析

由于振荡来流的速度呈周期性变化，这使得试验模型的泄涡频率也呈周期性变化，而传统的基于快速傅里叶变换的谱分析无法给出信号频率随时间变化的分布情况。因此，本文引入小波变换对所有的应变响应时历信号进行分析，得出随时间瞬时变化的响应频率以及信号振动强度的时频分布结果。

连续小波变换方程如下：

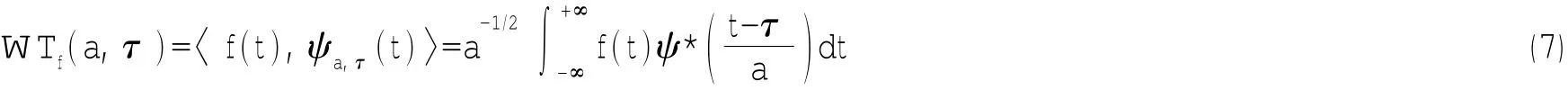
式中：WTf（a,τ）为对时历信号f（t）进行小波变换后得到的系数，表示时间尺度上的频率变化值，a为尺度因子，τ为平移因子，ψ（t）为小波母函数。本文选取Morlet小波函数，其定义为：

区别于传统涡激振动响应特性的谱分析方法，本文从时间历程的角度考察模型的泄涡频率、位移响应幅值及涡激振动响应频率的变化情况。

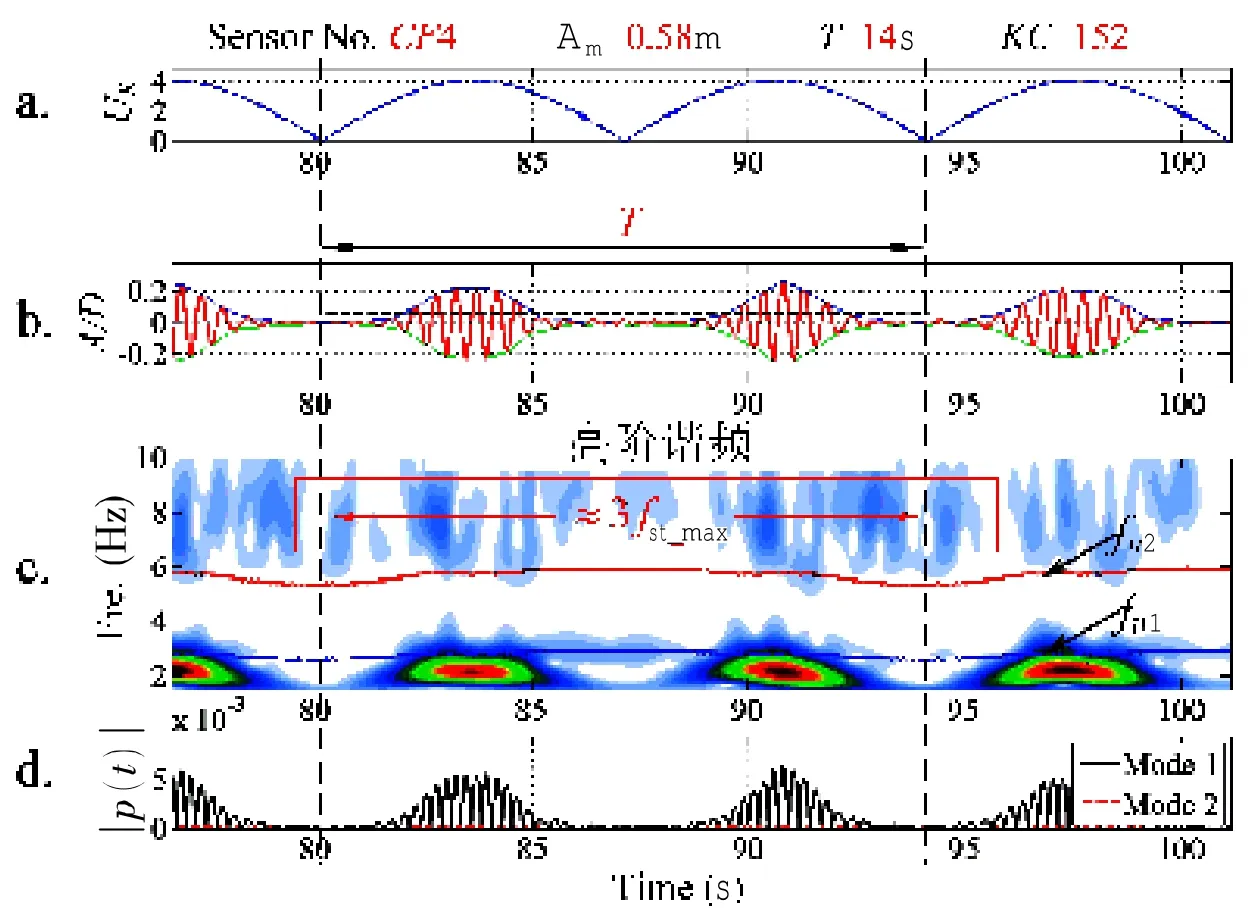
图4 工况（URmax=4;KC=152）结果图Fig.4 Results of case(URmax=4;KC=152)at CF4

图4为一典型的数据处理结果。图中包含以下67个方面的信息：

（1）应变测点位置为CF4（模型中间点在垂直来流方向上对应的测点，如图3所示）、振荡幅值Am=0.58 m、振荡周期T=14 s及振荡来流的KC=152。

（2）第a栏表示泄涡频率随时间的变化曲线。

（3）第b栏表示CF4测点经过模态分析后得到的位移时历曲线，从图中可以清晰地看出涡激振动的位移响应幅值在每个周期中的波动情况。

（4）第c栏的云图为对CF4测点应变时历信号进行小波变换后的结果。云图中横轴表示时间，纵轴表示振动频率，颜色的深浅表示信号的能量集中程度。通过小波结果可以直观地观察每个时刻应变的瞬时响应频率范围及其能量集中程度。

（5）第c栏中的云图中加入模型实时的固有频率变化曲线。固有频率可以根据下式计算得出：

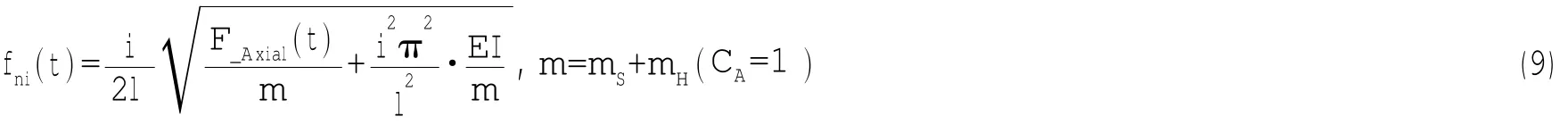
式中：fn（t）表示第i阶静水中结构瞬时固有频率值，F_Axial（t）为实时轴向张力值，m为模型质量（包括结构质量mS和附加质量mH，附加质量系数CA=1）。图中标出的红色波动细实线表示模型实时一阶固有频率值；黄色细实线表示模型实时二阶固有频率。

（6）第d栏表示第一、二阶位移模态权重随时间变化曲线（由模态分析法得到的pi（t））。这一信息清晰的展现出前每一瞬时时刻，前两阶位移模态在总振动中的参与情况。

3 振荡来流下涡激振动响应特性

经过对振荡来流下涡激振动的初步分析，已经确认振荡来流这种流体性质随时间变化的来流形式同样可以激励柔性圆柱体产生明显的涡激振动。并且其响应特性有着明显的“分时特性”[21]，主要体现于“振幅调制”与“模态转换”这两个基本特征。下文将进一步通过位移响应幅值分布、“迟滞”现象及“高阶谐频”三个角度进一步深入分析柔性立管在振荡来流下涡激振动的响应特性。

3.1 位移幅值响应特性

从图4中的b栏可以明显地看出每半个振荡周期中各监测点的位移响应幅值均存在着极值，总结各工况中的极值即可得到URmax=4、URmax=6.5及URmax=7.9时的位移响应幅值随KC数的变化趋势，分别如图5、图6及图7所示。

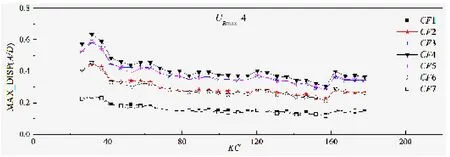
图5 URmax=4时，位移响应幅值随KC数分布图Fig.5 Maximum response amplitude distribution when URmax=4

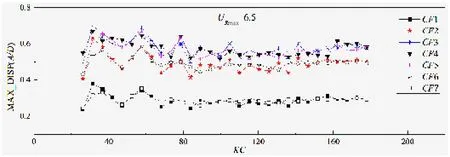
图6 URmax=6.5时，位移响应幅值随KC数分布图Fig.6 Maximum response amplitude distribution when URmax=6.5

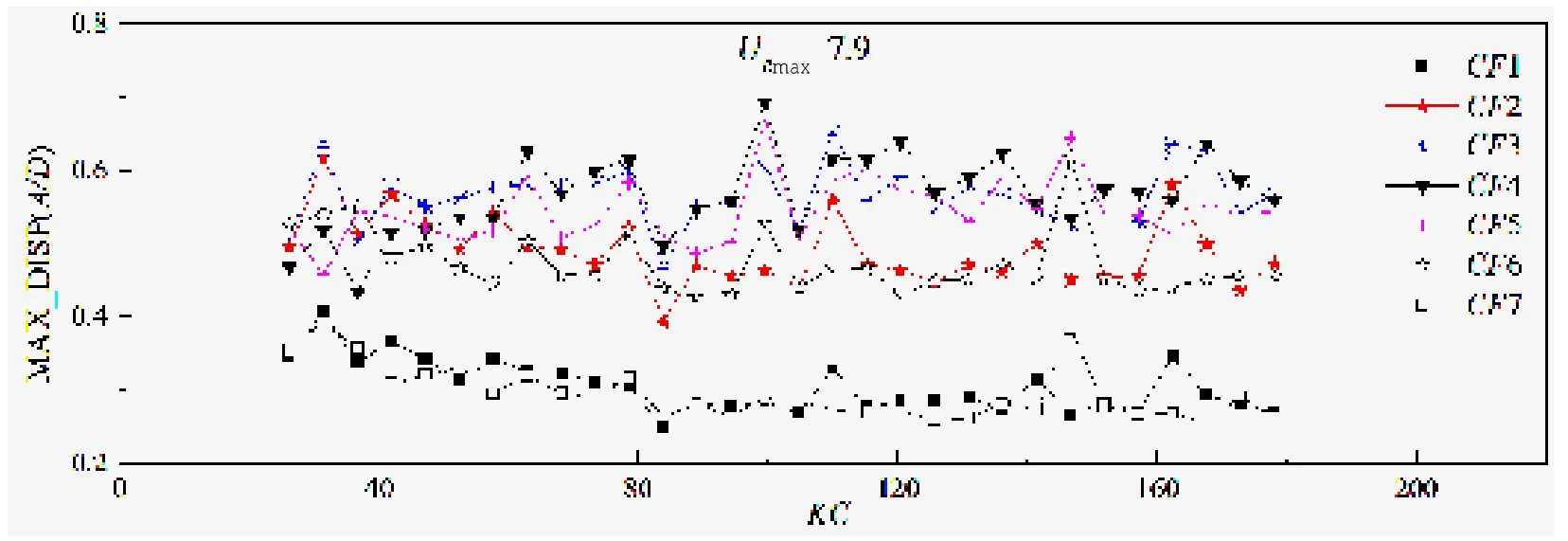
图7 URmax=7.9时，位移响应幅值随KC数分布图Fig.7 Maximum response amplitude distribution when URmax=7.9

当URmax=4，KC>40时，从图5中可以看出涡激振动位移响应幅值均出现在CF4测点（模型正中间位置），且其最大值为0.4D左右，可以看出这时模型的涡激振动响应由一阶模态主导。而当KC数较小时，位移响应幅值却显著增大。然而直观的认知是：KC数较小即意味着来流距离较短，这将没有足够的来流距离来生成稳定的涡泄，所以在KC数较小时，涡激振动现象应该趋于减弱。而图5中的结论是与传统的直观认知截然相反的，因此本文推测：模型尾部在上半个振荡周期中已经形成的漩涡，由于当KC数较小，没有足够的来流距离消耗这些已经生成的尾涡。但是模型随即反转方向继续作振荡运动，此时模型将不可避免地处于上半个振荡周期形成的尾涡中，而正是这些已经存在的尾涡在一定程度上增强了模型的涡激振动响应，从而出现小KC数工况却有着较大响应幅值的情况。

当URmax=6.5时，从图6中可以看出：对于不同的KC数，位移响应幅值的最大值分散出现在CF3，CF4或者CF5测点，位移幅值最大值基本稳定在0.5D左右，这明显是由于二阶模态的参与引起的。同样的，当KC数较小时出现位移幅值稍大的情况，这也是因为上个振荡半周期中形成的尾涡一定程度上增强了下半周期的涡激振动响应。

当URmax=7.9时，从图7中可以看出：位移响应幅值的最大值随KC数的变化没有明显的规律，位移幅值最大值基本在0.6D上下浮动。并且可以明显看出部分工况中，对称测点（如CF3与CF5，如图3所示）对应的幅值并不相等，这里推测是由于当URmax=7.9时，发生了明显的“模态转换”现象，如图13所示。“模态转换”意味着模型在不同时刻的响应由不同模态主导，这种很强的时域特征将给振荡来流下的涡激振动带来更多的不确定性。因此未来十分有必要进行更多的激励高阶模态响应的试验。

3.2 迟滞

前文提到，振荡来流本质上就是流速随时间正弦变化的一种特殊来流形式：不仅流速实时变化，来流方向也在每个周期中变化一次。如图8所示，振荡来流实际上又可看作加速段和减速段的组合。对于传统定常来流作用下柔性立管普遍存在“迟滞”现象，即对于某一固定约化速度，加速段响应幅值低于减速段响应幅值[22]。因此推测对于振荡来流这种特殊来流，应该也会出现“迟滞”现象。对于本文中的试验工况，将试验结果分为加速段与减速段两部分分析。图8中，上图中的每个时刻的约化速度值均对应着下图中唯一的位移响应幅值。这样，可以得到加速段、减速段中响应幅值A/D-约化速度UR曲线图，通过对比分析来判断“迟滞”是否发生。

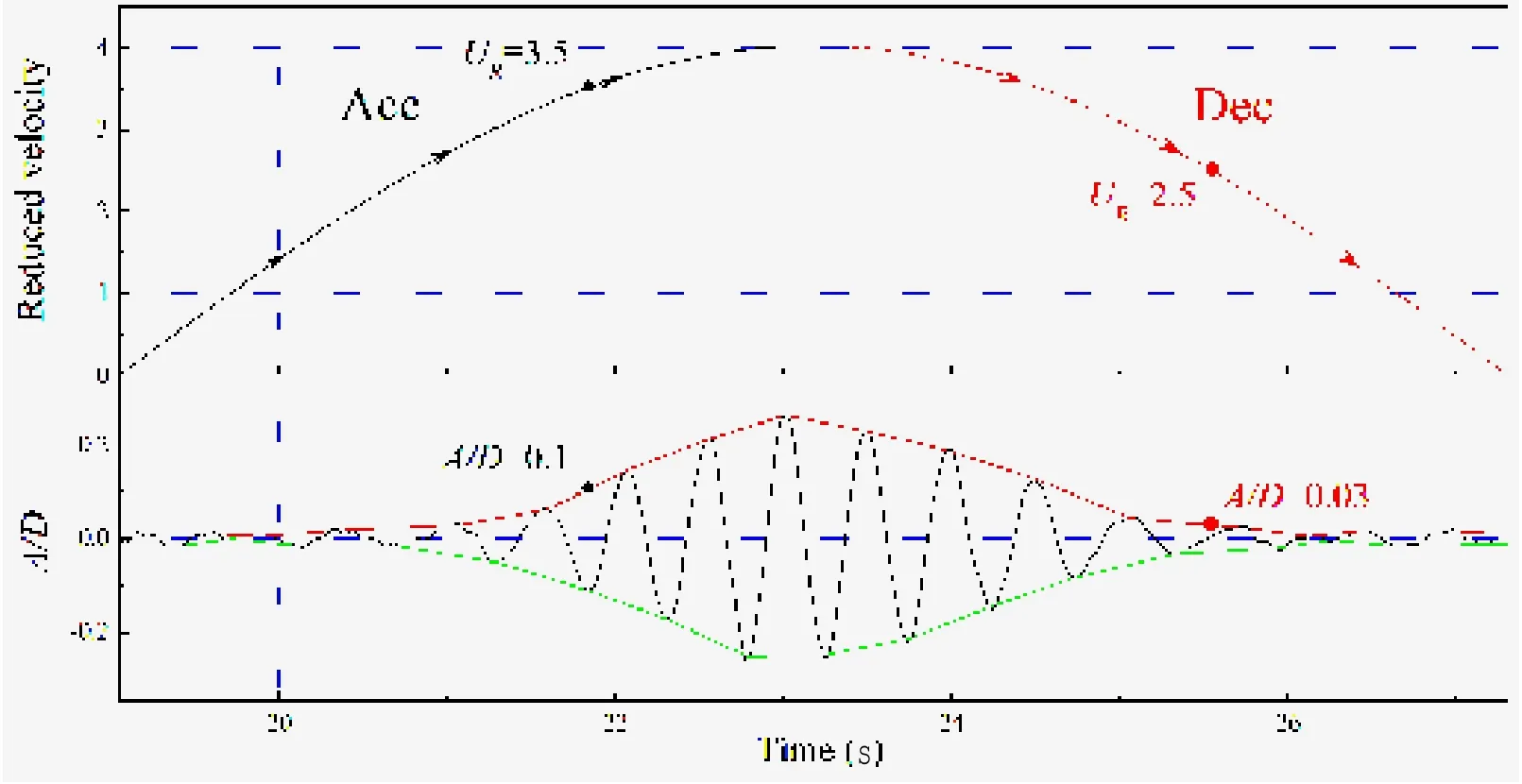
图8 获取不同约化速度下响应幅值示意图Fig.8 Schematic diagram of obtaining A/D vs URplot

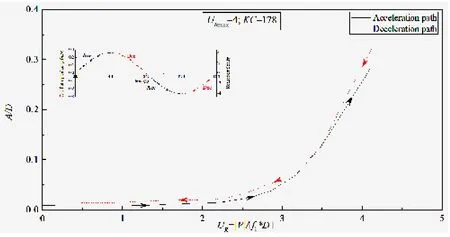
图9 工况（URmax=4；KC=152）中迟滞结果Fig.9 Hysteresis in case(URmax=4;KC=152)at CF4

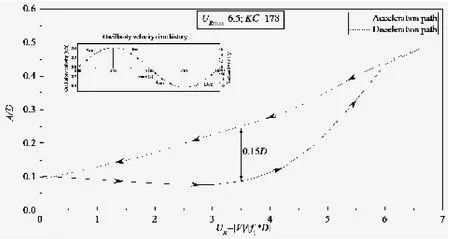
图10 工况（URmax=6.5；KC=152）中迟滞结果Fig.10 Hysteresis in case(URmax=6.5;KC=152)at CF4

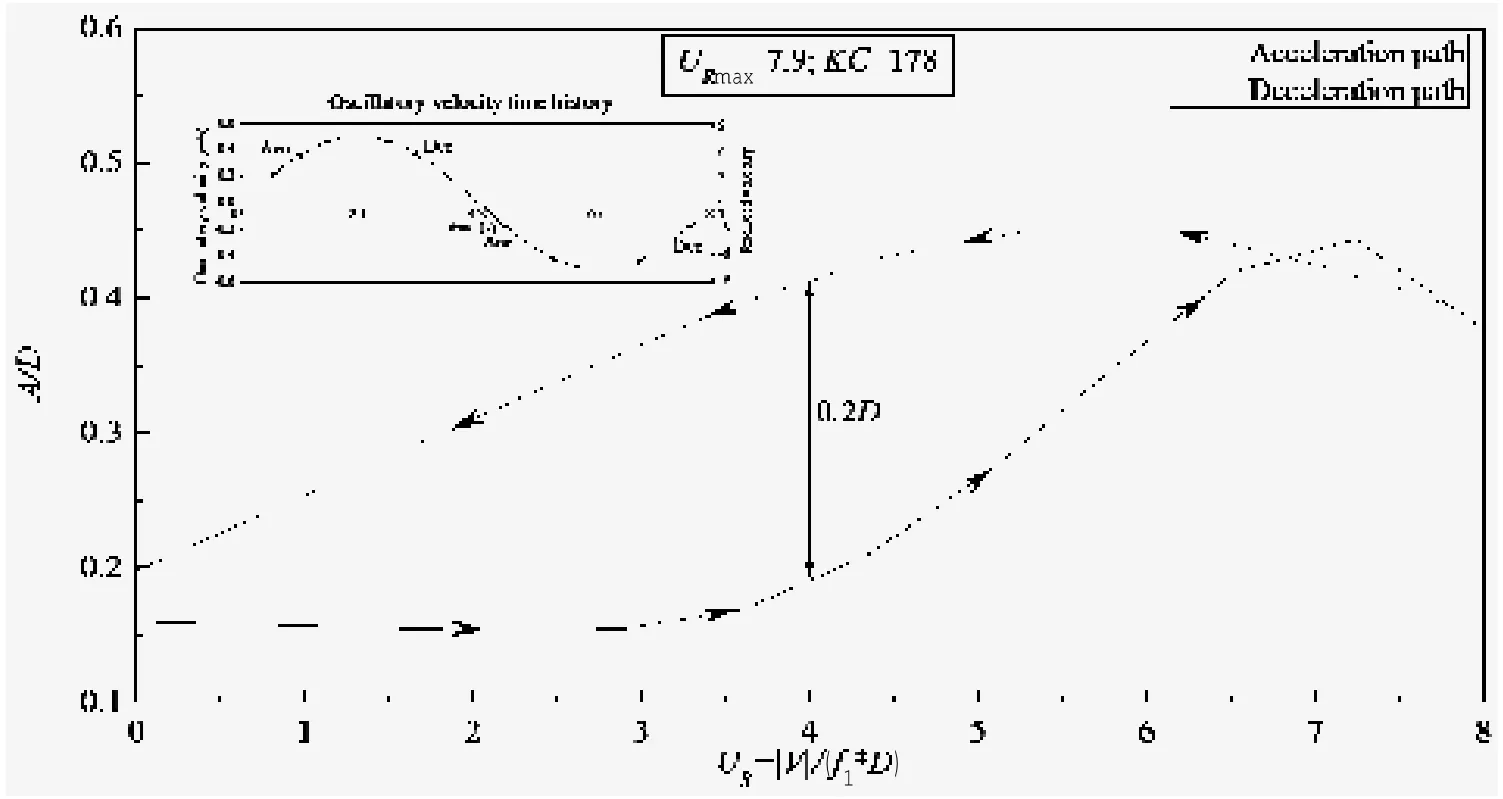
图11 工况（URmax=7.9；KC=152）中迟滞结果Fig.11 Hysteresis in case(URmax=7.9;KC=152)at CF4

本文将以KC=152对应的3个工况进行分析。如图9所示为最大约化速度URmax=4，KC=152时的响应幅值A/D-约化速度UR曲线图。可以看出位移响应幅值在加速段与减速段基本重合，并没有发生“迟滞”现象。而对于如图10所示的URmax=6.5，KC=152工况的结果图中，可以明显看出减速段的位移响应幅值要明显高于加速段，并且其位移最大差值达到0.18D。同样，“迟滞”现象在图11所示的工况URmax=7.9，KC=152也非常显著，其位移最大差值达到0.17D。本文中观察到的“迟滞”现象与刚性圆柱体自激振荡试验中观察到的“迟滞”现象是有本质的区别的。刚性圆柱体的“迟滞”现象是由泻涡模式的变化而引起的[20]。而对于本文的试验工况，其存在着明显的“模态转换”：加速段对应着从一阶模态锁定到二阶模态锁定的转换，而减速段则对应着二阶模态锁定到一阶模态锁定的转换，这将必然导致同一个约化速度下，减速段的位移响应幅值大于加速段，即如图10和图11展现出的“迟滞”。

3.3 高阶谐频响应

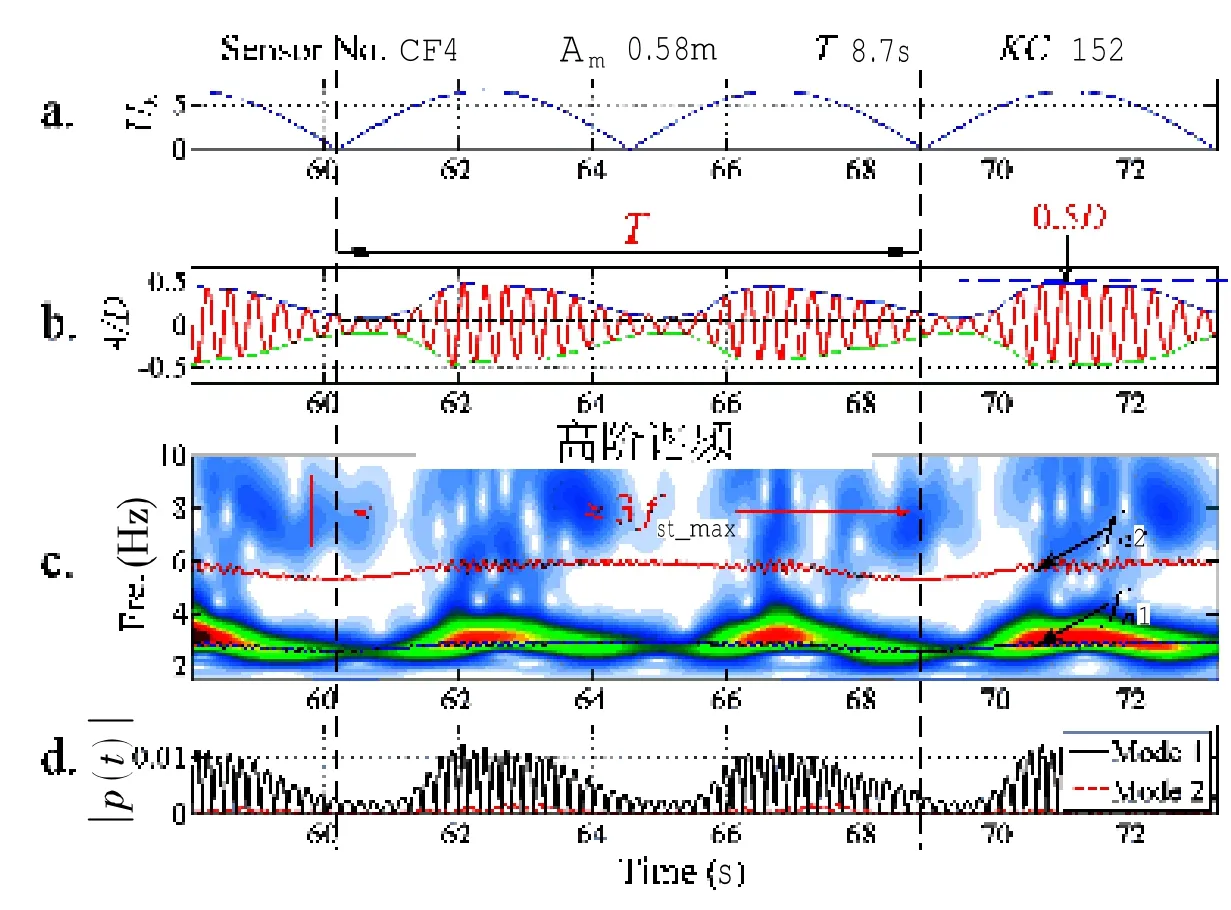
图12 工况（URmax=6.5;KC=152）结果图Fig.12 Results of case(URmax=6.5;KC=152)at CF4

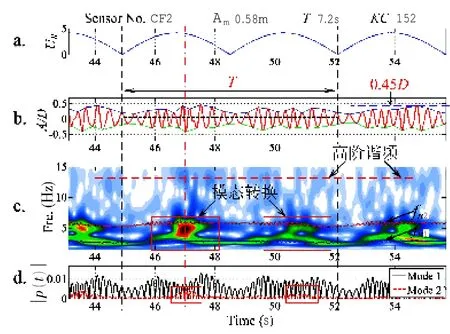
图13 工况（URmax=7.9;KC=152）结果图Fig.13 Results of case(URmax=7.9;KC=152)at CF4

从小波时频图中，可以观察到模型的响应频率在时间轴上的分布情况。值得注意的是，本文的试验工况中也发现了高阶的响应频率，其频率值大约为基本响应频率的3倍，如图4、图12及图13所示。对于这种奇数倍基频的高阶频率响应，国外学者发现其几乎存在于所有的定常来流下柔性立管涡激振动实验中[23]，通过对这种高阶谐频响应造成的疲劳贡献进行了详细的分析，发现计算疲劳损伤的贡献时必须计及这种高阶谐频响应，否则将大大降低设计安全系数。另外，国外学者已经通过PIV实验得出结论：这种高阶谐频响应是由于模型的顺流向的运动响应使得泻涡模式呈“2T”形式，从而在垂直于来流方向形成高阶谐频的泻涡力[24]。据此推测本文中的高阶谐频响应也是由“2T”的泻涡模式引起的，为进一步证实这一结论，还需开展相关机理性试验研究。

4 结 语

本文进行了振荡流作用下柔性立管的涡激振动试验，试验主要研究最大泻涡频率URmax以及KC数对涡激振动响应特性的影响。结合小波分析与模态分析法处理试验数据，通过结果的对比分析，得到以下结论：

（1）振荡来流下涡激振动的位移响应幅值随着最大约化速度URmax的增大而增大。对于某一特定的URmax，当KC数较大时，响应幅值相对稳定，而当KC数较小时，由于前半个振荡周期中尾涡的影响，将出现较大的幅值响应。

（2）当最大约化速度URmax较大时，观察到了显著的“迟滞”现象，这主要是由于振荡来流的加减速引起的“模态转换”而引起的。

（3）试验中发现了3倍于涡激振动基本响应频率的“高阶谐频”响应，虽然其高阶响应成分幅值相对较小，但其响应频率很高，这就同样能给结构带来可观的疲劳损伤。这一现象在未来的疲劳损伤计算时必须考虑入内。

（4）振荡来流作用下的立管涡激振动有着很强的“时域特性”，未来需要从振荡来流的基本参数：URmax及KC数着手，紧密结合以上总结的基本特性，发展新的振荡来流作用下涡激振动预报模型。

[1]Vandiver J K,Li Li.SHEAR7 V4.4 Program Theoretical Manual[M].Department of Ocean Engineering,MIT.,2005:32.

[2]Larsen C M,Vikestad K,Rttervik R,Passano E,Baarholm G S.VIVANA,Theory Manual[M].MARINTEK,Trondheim, 2001.

[3]Griffin O M,Vandiver J K.Vortex-induced strumming vibrations of marine cableswith attached masses[J].ASME Journal of Energy Resources Technology,1984,106:458-485.

[4]Lie H,Kaasen K E.Modal analysis of measurements froma large-scale VIV model test of a riser in linearly sheared flow[J]. Journal of Fluids and Structures,2006,22(4):557-575.

[5]Halse K H,Mo K.Vortex Induced Vibrations of a catenary riser[C]//3rd International Symposium on Cable Dynamics. Trondheim,1999:103-110.

[6]Allen D W(Don),Henning D L.Prototype Vortex-Induced Vibration tests for production risers[C]//Pro.of the OTC.Houston,USA,2001,Paper OTC 2001-13114.

[7]Tognarelli M A,et al.VIV response of a long flexible cylinder in uniform and linearly sheared currents[C]//Pro.of the OTC.Houston,USA,2004,Paper OTC 2004-16338.

[8]Wilde D E,Huijsmans J J,Rene H M.Laboratory investigation of long riser VIV response[C]//ISOPE Conference.Toulon, 2004.

[9]Chaplin J R,et al.Laboratory measurements of vortex-induced vibrations of a verticaltension riser in a stepped current[J]. Journal of Fluids and Structures,2005,21:3-24.

[10]Trim A D,Braaten H,et al.Experimental investigation of vortex-induced vibration of long marine risers[J].Journal of Fluids and Structures,2005,21:335-361.

[11]Vandiver J K,et al.High mode number Vortex-Induced Vibration field experiments[C]//Pro.of the OTC.Houston,USA, 2005,Paper OTC 2005-17383.

[12]Fu S.Experimental investigation on VIV of the flexible model under full scale Re number[C]//30thOMAE.Rotterdam, 2011,Paper No.OMAE2011-49042.

[13]唐国强,吕 林,滕 斌,等.大长细比柔性杆件涡激振动试验[J].海洋工程,2011,29(1):18-25. Tang Guoqiang,Lü Lin,Teng Bin,et al.Experimental investigation on Vortex-induced Vibration of large aspect ratio structures[J].Ocean Engineering,2011,29(1):18-25).(in Chinese)

[14]张永波,郭海燕,孟凡顺,等.基于小波变换的顶张力立管涡激振动规律试验研究[J].振动与冲击,2011,30(2):149-154. Zhang Yongbo,Guo Haiyan,Meng Fanshun,et al.Experimental investigation of Vortex-Induced Vibration of top tension riser based on wavelet transform[J].Journal of Vibration and Shock,2011,30(2):149-154.(in Chinese)

[15]雷 松,郑向远,张文首,等.海洋立管悬挂状态的固有频率和振型[J].船舶力学,2015,19(10):1267-1274. Lei Song,Zheng Xiangyuan,Zhang Wenshou,et al.Natural frequencies and mode shapes of free-hanging risers[J].Journal of Ship Mechanics,2015,19(10):1267-1274.(in Chinese)

[16]高 云,付世晓,熊友明,等.表面粗糙度对立管涡激振动响应影响的试验研究[J].船舶力学,2015,19(1-2):1-15. Gao Yun,Fu Shixiao,Xiong Youming,et al.Experimental study of the effects of surface roughness on the vortex-induced vibration response of a riser[J].Journal of Ship Mechanics,2015,19(1-2):1-15.(in Chinese)

[17]Grant R G,Litton R W,Mamidipuli P.Highly Compliant Rigid(HCR)riser model tests and analysis[C]//Offshore Technology Conference.Houston,1999,Paper No.OTC 1999-10973.

[18]mark Chang S H,Isherwood M.Vortex-Induced Vibrations of steel catenary risers and steel offloading lines due to platform heave motions[C]//Offshore Technology Conference.Huston,2003,Paper No.OTC 2003-15106.

[19]Liao Jung-Chi.Vortex-induced Vibration of slender structures in unsteady flow[D].Boston:Massachusetts Institute of Technology,2002.

[20]Gonzalez E C.High Frequency dynamic response of marine risers with application to flow-induced vibration[D].Boston: Massachusetts Institute of Technology,2001.

[21]Fu Shixiao,Wang Jungao,Baarholm R,Wu J,Larsen C M.VIV of flexible cylinder in oscillatory flow[C]//32nd OMAE. Nantes,2013,Paper No.OMAE2013-10348.

[22]潘志远.海洋立管涡激振动机理与预报方法研究[D].上海:上海交通大学,2005. Pan Zhiyuan.Vortex-induced Vibration of marine riser and response prediction[D].Shanghai:Shanghai Jiao Tong University,2005.

[23]Price P,Zheng H,Modarres-Sadeghi Y,Triantafyllou M S.Effect of higher harmonics and spectral width on fatigue damage of marine risers[C]//30thOMAE.Rotterdam.2011,Paper No.OMAE2011-49728.

[24]Williamson C H K,Govardhan R.Vortex-induced vibrations[J].Annual Review of Fluid Mechanics,2004,36:413-455.

Experimental investigation on Vortex-Induced Vibration of a flexible cylinder in oscillatory flow

WANG Jun-gao,FU Shi-xiao,XU Yu-wang,SONG Lei-jian
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240)

Under the top vessel motions,dynamic responses of the catenary risers would generate relatively oscillatory flow around themselves.Such oscillatory flow would easily trigger the‘intermittent VIV'at sag-bend part of the riser.This paper mainly focuses on the experimental investigations on the behaviors of a flexible cylinder in oscillatory flow with different combinations of both maximum reduced velocity URmaxand KC number.Fiber Brag Grating(FBG)strain sensors were used to measure the VIV response of the model cylinder.Then,modal analysis and wavelet analysis were utilized to study the experimental data,VIV responses in oscillatory flow and the effects from both reduced velocity and KC number were discussed and summarized.Furthermore,novel features such as higher harmonics and hysteresis were observed.

oscillatory flow;Vortex-Induced Vibration;hysteresis;higher harmonics

P756.2

：Adoi:10.3969/j.issn.1007-7294.2016.04.005

1007-7294（2016）04-0419-11

2015-11-23

国家自然科学基金（51279101；51490674；51490675）

王俊高（1989-），男，博士研究生；付世晓（1976-），男，研究员，博士生导师，通讯作者，E-mail:shixiao.fu@sjtu.edu.cn。