改进的基于特征线的N-S方程算子分裂有限元法

水庆象，王大国，沈连山

（1西南科技大学环境与资源学院，四川绵阳621010；2大连大学信息工程学院，辽宁大连116622）

改进的基于特征线的N-S方程算子分裂有限元法

水庆象1，王大国1，沈连山2

（1西南科技大学环境与资源学院，四川绵阳621010；2大连大学信息工程学院，辽宁大连116622）

基于特征线的Navier-Stokes（N-S）方程算子分裂有限元法（CBOS有限元法）的核心是在每一个时间层上，采用算子分裂法将N-S方程的对流项和扩散项分开求解；对流项的求解过程借鉴了简单显式特征线时间离散，显式求解。该文在原CBOS有限元法基础上推导了一种更加精确的对流项显式离散方法。通过自编程序对方腔流进行数值模拟，表明该算法具有更高的计算精度。低雷诺数下圆柱绕流计算所得的阻力系数、升力系数、斯特劳哈数等与已有数据较为接近，表明该文中算法能较准确地模拟圆柱绕流的流场特性；最后，文中分析了Re= 200时圆柱绕流在一个周期内所受升力变化与对应流场中压力和流线演化的关系。

N-S方程；CBOS有限元法；方腔流；圆柱绕流

0 引 言

N-S方程的动量方程中存在对流项导致方程不具备自伴随性，尤其当雷诺数较大使得对流占优时，方程会呈现出强非线性特性，采用标准Galerkin有限元法求解将导致数值解的振荡。针对对流项占优时导致数值解振荡的问题，自20世纪80年代以来，已有多种有别于标准Galerkin有限元的新算法问世。目前应用较为广泛的有Petrov-Galerkin法[1]、Taylor-Galerkin法[2]、Galerkin最小二乘法[3]和特征线Galerkin法[4]等。其中，特征线Galerkin法的基本思想是将N-S方程的动量方程沿特征线进行时间离散，以理性形式引入稳定项，具有比较明确的物理意义。1995年，Zienkiewicz和Codina[5]将Taylor展开法引入到特征线Galerkin法中并将其与分离算法相结合，提出了基于特征线的分离算法（CBS），该方法可以直接由N-S方程推导出合理的平衡耗散项，从而可以获得稳定的数值解。王大国等人[6]结合了CBS算法和算子分裂法[7]的优点，提出了基于特征线的算子分裂有限元法（CBOS有限元法）求解二维非定常不可压N-S方程，但没有对圆柱绕流进行数值模拟。

CBOS有限元法根据N-S方程的特性，采用算子分裂法将N-S方程分裂成对流项和扩散项，这种分裂方法既能考虑方程的扩散性质，又能突出对流占优的特性。对流项的求解借鉴了CBS法的简单显式特征线时间离散，它的思想包括局部Taylor展开。然而原CBOS有限元法中为了获得对流项的完全显示的计算格式做了一定的近似而导致算法的精度降低，本文在原CBOS有限元法基础上推导了一种更加精确的对流项显示离散方法。通过自编程序对方腔流进行数值模拟，表明该算法具有更高的计算精度。低雷诺数下圆柱绕流计算所得的阻力系数、升力系数、斯特劳哈数等与已有数据较为接近，表明该算法能较准确地模拟圆柱绕流的流场特性；最后本文分析了Re=200时圆柱绕流在一个周期内所受升力变化与对应流场中压力和流线演化的关系。

1 控制方程

二维非定常粘性不可压缩流动（忽略能量损失）可由连续方程和N-S方程（统称N-S方程）控制，其无量纲形式表示为

式中： （ui,ui）=（u,v），u为水平方向速度，v为垂直方向速度，p为压强，t为时间，Re为雷诺数，f1为水平方向外力，f2为垂直方向外力，（xi,xi）=（x,y）。

2 计算方法

2.1 算子分裂法

本文采用算子分裂法将控制方程（1）和（2）分成扩散项

和对流项

2.2 对流项的特征线法显式时间离散

中的沿流线的稳定扩散项是不同的。由于稳定扩散项在高雷诺数或可压缩流动计算中是抑制振荡尤其是压力振荡的基础[8]，所以采用改进的CBOS有限元法对流动问题进行数值模拟将会在计算域内得到更为稳定的压力分布。

3 有限元求解

3.1 扩散项有限元求解

扩散项中出现了速度和压力变量，采用混合有限元求解，为满足LBB条件取单元为九节点四边形单元，速度插值采用九节点，压力插值采用四节点（单元的角节点），应用标准Galerkin法对上式进行有限元空间离散，可得

式中：Nα和Nβ为二次插值函数，Ml为线性插值函数，α=1,2,…,m，β=1,2,…,m，l=1,2,…,h，m=9为插值单元内速度节点个数，h=4为插值单元内压力节点个数，δij为置换算子，δijuiβ=ujβ。

3.2 对流项有限元求解

同扩散项处理方法一样，由标准Galerkin法建立（20）式的弱形式（省略上标）

对上式最后一项分部积分（忽略边界项的影响）得

式中：Nγ和Nη为二次插值函数，γ，η=1,2,…,m。

4 边界条件处理及求解过程

本文采用改进的CBOS有限元法求解N-S方程，求解过程中只需给出扩散项的边界条件，扩散项是一个抛物型方程，边界条件见后面具体的数值模型。本文算法的求解过程如下：

（3）转到下一时刻，重复步骤（1）、（2）。

5 数值验证

5.1 方腔流验证

方腔流是流体力学中用来检验数值模拟可靠性的经典算例，利用本文所建立的模型对方腔流进行数值模拟。如图1，方腔无量纲尺度为1×1，内部流体的初始速度和压力都是零；顶边施加无量纲速度u=1，v=0，其他三边上都是固壁，施加无滑移边界条件u=0，v=0。坐标原点在方腔左下角，在该点置相对压力p=0。整个计算域划分为30×30个九节点四边形单元，共有3 721个节点。

图1 方腔流几何构型和边界条件Fig.1 Cavity flow configuration and boundary conditions

5.2 不同雷诺数下的计算情况

图2给出了不同雷诺数下水平速度u沿垂直中线、垂向速度v沿水平中线的分布结果。图中实线表示本文计算结果，虚线表示原CBOS有限元法[6]的计算结果，点表示Ghia等人[9]的计算结果。图2（a）给出Re=1 000、Δt=0.005、t=28时的结果；图2（b）给出Re=5 000、Δt=0.001、t=110时的结果；图2（c）给出Re=5 000、Δt=0.01、t=110时的结果。从图2（a）和图2（b）可以看出，改进前后的CBOS有限元法计算结果比较接近，且与Ghia等人[9]的计算结果符合较好。但在较大时间步长情况下，本文算法计算结果比原CBOS有限元法计算结果具有更高的计算精度，这从图2（b）和图2（c）可以看出。

图2 速度沿中线分布（实线：本文计算结果；虚线：原CBOS有限元法[6]的计算结果；点：Ghia等人[9]的计算结果）Fig.2 Velocity along lines through geometric center

5.3 改进的CBOS法对压力的影响

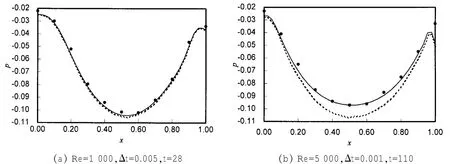
图3 压力沿水平中线分布（实线：本文计算结果；虚线：原CBOS有限元法[6]的计算结果；点：CBS法[8]的计算结果）Fig.3 Pressure along horizontal center line

图3给出了方腔流压力p沿垂直中面分布结果。图中实线表示本文计算结果，虚线表示原CBOS有限元法[6]计算结果，点表示CBS算法（半隐式格式）[8]的计算结果。图3（a）给出Re=1 000、Δt=0.005、t=28时的结果；图3（b）给出Re=5 000、Δt=0.001、t=110时的结果。由图3可以看出，本文算法计算的压力更加接近CBS算法的计算结果，且雷诺数越大，压力的改进越大。究其原因，是由于改进前后的CBOS有限元法引入了不同的沿流线的稳定扩散项，相关研究[8]表明稳定扩散项在高雷诺数或可压缩问题中相当重要，它可以有效地控制压力的振荡。

6 圆柱绕流工程应用

圆柱绕流是一个经典的流体力学问题，是最具代表性的钝体绕流问题，本文对Re=100和Re=200的圆柱绕流进行了数值研究。

6.1 计算区域、网格划分和边界条件

取圆柱直径D=0.1，计算区域尺度在主流方向上取为30D，其中圆柱上游分配10D，横向尺寸为18D，入口处指定无因次水平速度为u=1，横向速度v=0；侧壁采用可滑移边界条件；圆柱表面为不可滑移边界条件；出口处为自由出流边界，并指定相对压力为p=0。整个计算域划分为2 964个九节点四边形单元，共有12 114个节点，由于圆柱附近流场比较复杂，含有涡旋的生成与脱落等现象，需要布置较密的网格；而在远离圆柱的区域则可布置较疏的网格以节省计算量，具体的网格划分如图4所示。

图4 计算区域网格划分Fig.4 Sketch of computation grid

6.2 阻力系数、升力系数以及斯特劳哈数的比较

（30）式中f0表示涡的自然脱落频率。

表1 Re=100和Re=200时本文计算结果与其他文献数据的比较Tab.1 Comparison between calculated results with data provided by other references at Re=100 and Re=200

续表1

从表1中可以看出，本文的计算结果与相关参考文献的数值结果符合较好。图5给出了圆柱绕流的升力系数和阻力系数时程曲线，从图中可以发现阻力脉动频率为升力的2倍。

图5 升力和阻力时程曲线（实线：阻力系数，虚线：升力系数）Fig.5 Variations of lift coefficient and drag coefficient with time

6.3 升力的周期变化与流场的演化

图6给出了Re=200时的固定圆柱绕流一个涡旋脱落周期内升力系数的时程曲线，图7给出了Re=200时的固定圆柱绕流在大致一个涡旋脱落周期内的压力和流线的演化过程。图6中的●点与图7中各时刻流场图一一对应。

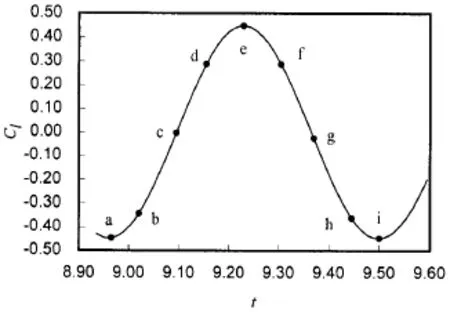
图6 一个涡旋脱落周期内升力时程曲线Fig.6 Time variations of lift coefficient in a cycle

图7（a）给出了当t=8.96时流场的压力云图和流线图，可以看出，圆柱下方压力偏低，上部压力相对较高，这在圆柱的背流面表现得更为明显，因此圆柱在总体上受到负向压力作用。在同一时刻的流线图中，圆柱背流面的下部存在一个贴体主涡旋区，该涡旋区同时对应流场中的主低压区；而在圆柱表面背流面上部出现流动分离趋势，在分离点后方的压力为高压区，该高压区与圆柱正上方表面的低压分布正好形成逆压梯度，逆压梯度驱动近壁面流体倒流产生分离。

图7 Re=200时一个周期内的压力和流线演化Fig.7 The development of pressure and streamline during a cycle at Re=200

随着时间的发展，在t=9.02时可以发现，圆柱附近的贴体主涡开始脱离壁面，主低压区也开始远离圆柱，导致圆柱背流面下方壁面上的压力升高；与此同时，由流线图可知在原分离点位置形成较明显的分离涡旋，压力也相应减小。上述压力和流线的演化导致圆柱在总体上所受的负向压力减小，这与升力时程曲线由a到b的变化情况相符。

在t=9.10时刻对应于圆柱所受升力基本为零的状态。在时间为9.02～9.10阶段伴随着圆柱背流面上部涡旋区扩大，临近区域的压力持续降低，圆柱尾迹区的主漩涡则向下游进一步推移，相应的低压区也更进一步地远离壁面，圆柱背流面下部附近的压力继续增大。圆柱背流面上部压力减小与下部压力增大趋势的持续发展将导致圆柱所受负向升力持续减小直至出现为零，如升力时程曲线上的c点。之后，涡流场的这一演化持续进行，当圆柱背流面下部压力在总体上高于背流面上部压力时，圆柱受到正向升力的作用，如图7（d）所示在t=9.16时的流场图。

当t=9.22时作用于圆柱上的正向升力达到最大。圆柱背流面下部的主涡旋已经基本消散，此时流场中的贴体主涡旋区位于圆柱背流面上方，并于此形成低压区；在圆柱背流面下部近壁面则出现了新的流动分离，该区域压力达到半个周期来的最大，对比图7（a）和图7（e）可以发现两幅图的流线的空间分布恰好相反。此后圆柱受力状态进入正向升力减小阶段，流线以及压力的演化规律类似于前半个周期的情况，分别将图7（f）与图7（b）、图7（g）与图7（c）、图7（h）与图7（d)对比可以发现以上各对流线和压力分布都比较相似，只是空间分布相反。这种对称演化过程也充分体现了升力的周期性变化特征。

当t=9.50时，圆柱所受升力又重新达到负向最大，相应的涡旋分离、脱落与压力分布也完成了一个周期的演化过程。

7 结 论

（1）在原CBOS有限元法[6]基础上，推导了一种更加精确的对流项显式离散格式。通过方腔流的数值模拟，发现当时间步长较大时，本文算法计算结果比原CBOS有限元法计算结果更接近Ghia等人[9]的计算结果。同时，相对原CBOS有限元法，本文算法压力的计算结果与CBS法[8]压力的计算结果更加吻合，尤其是在高雷诺数的情况下压力的改变更加明显，究其原因，主要是由于本文算法引入了不同的沿流线的稳定扩散项，稳定扩散项在高雷诺数或可压缩问题中相当重要，它可以有效地控制压力的振荡。

（2）通过对低雷诺数的圆柱绕流进行数值模拟，计算所得的阻力系数、升力系数、斯特劳哈数等与参考文献中的值较为接近，表明本文提出的算法能较准确地模拟圆柱绕流的流场特性。通过对Re= 200的圆柱绕流在一个周期内所受升力的变化及其相应的流场中的压力和流线演化分析可知：当圆柱所受升力达到最大（负向最大或者正向最大）时，在圆柱后方尾流区内的一侧存在明显的贴体涡旋，同时在圆柱表面尾流区内的另一侧由于逆压梯度的驱动开始出现流动分离现象。

[1]Christie I,Griffiths D F,Mitchell A R,et al.Finite element methods for second order differential equations with significant first derivatives[J].International Journal for Numerical Methods in Engineering,1976,10(6):1389-1396.

[2]Donea J.A Taylor-Galerkin method for convective transport problems[J].International Journal for Numerical Methods in Engineering,1984,20(1):101-119.

[3]Hughes T J R,Franca L P,Hulbert G M.A new finite element formulation for computational fluid dynamics:VIII.The Galerkin/least-squares method for advective diffusive equations[J].Computer Methods in Applied Mechanics and Engineering,1989,73(2):173-189.

[4]Pironneau O,Liou J,Tezduyar T.Characteristic-Galerkin and Galerkin/least-squares space-time formulations for the advection-diffusion equation with time-dependent domains[J].Computer Methods in Applied Mechanics and Engineering, 1992,100(1):117-141.

[5]Zienkiewicz O C,Codina R.A general algorithm for compressible and incompressible-flow,I:The split characteristic based scheme[J].International Journal for Numerical Methods in Fluids,1995,20(8-9):869-885.

[6]Wang Daguo,Wang Haijiao,Xiong Juhua,et al.Characteristic-based Operator-splitting Finite Element Method for Navier-Stokes equations[J].Science in China(Series E),2011,54(8):2157-2166.

[7]Glowinski R,Pironneau O.Finite element method for Navier-Stokes equations[J].Annual Review of Fluid Mechanics, 1992,24(1):167-204.

[8]Zienkiewicz O C,Taylor R L.有限元方法（第五版）第三卷流体动力学[M].符 松,刘扬扬译.北京:清华大学出版社, 2008.

[9]Ghia U,Ghia K N,Shin C T.High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J].Journal of Computational Physics,1982,48(3):387-411.

[10]Liu Z,Zheng X,Sung C H.Preconditioned multi-grid methods for unsteady incompressible flows[J].Journal of Computational Physics,2000,160(1):151-178.

[11]Wu G X,Hu Z Z.Numerical simulation of viscous flow around unrestrained cylinders[J].Journal of Fluids Structures, 2006,22(3):371-390.

[12]Xu S,Wang Z J.An immersed interface method for simulating the interaction of a fluid with moving boundaries[J].Journal of Computational Physics,2006,216(2):454-493.

[13]Mahfouz F M,Badr H M.Flow structure in the wake of a rotationally oscillation cylinder[J].Journal of Fluids Engineering, 2000,122(2):290-301.

[14]魏志理,孙德军,尹协远.圆柱尾迹流场中横向振荡翼型绕流的数值模拟[J].水动力学研究与进展,2006,21(3):299-308. Wei Zhili,Sun Dejun,Yin Xieyuan.A numerical simulation of flow around a transversely oscillating hydrofoil in the wake of a circular cylinder[J].Journal of Hydrodynamics,2006,21(3):229-308.

The pivotal ideas of characteristic-based operator-splitting(CBOS)finite element method for Navier-Stokes equations are that the equations are split into the diffusive part and the convective part by adopting the operator-splitting algorithm in each time step.The convective part can be discretized using the simple explicit characteristic temporal discretization and solved explicitly.On the basis of CBOS finite element method,an exact explicit discrete method is developed.The improved method has higher calculation accuracy through numerical simulation of lid-driven cavity flow.Furthermore,the method is used to simulate the incompressible viscous flow around cylinder with low Reynolds number.The numerical results agree well with other numerical results,which proves that it can exactly simulate the characteristics of flow around cylinder.Finally,the relationship between a cycle of lift coefficient and the corresponding development of pressure and streamline is analyzed at Re=200.

N-S equations;CBOS finite element method;lid-driven cavity flow;flow around cylinder

O35

：Adoi:10.3969/j.issn.1007-7294.2016.04.001

1007-7294（2016）04-0381-12

2015-11-15

国家自然科学基金（51349011，41072235）

水庆象（1988-），男，硕士，讲师；王大国（1975-），男，博士，教授，通讯作者，E-mail:dan_wangguo@163.com。

Improved characteristic-based operator-splitting finite element for Navier-Stokes equations SHUI Qing-xiang1,WANG Da-guo1,SHEN Lian-shan2

(1 School of Environment and Resource,Southwest University of Science and Technology,Mianyang 621010,China; 2 Department of Information Engineering,Dalian University,Dalian 116622,China)