两自由度不同截面形式柱体涡激振动的CFD数值模拟

赵 婧，郭海燕

（中国海洋大学 工程学院，山东 青岛 266100）

两自由度不同截面形式柱体涡激振动的CFD数值模拟

赵 婧，郭海燕

（中国海洋大学 工程学院，山东 青岛 266100）

文章采用计算流体力学（CFD）方法，结合SST k-ω湍流模型，对低质量比柱体进行两自由度涡激振动数值模拟，得到了柱体升力、曳力系数的时程曲线，并观察了柱体进入锁振状态的幅值变化，研究了不同截面形式柱体在外流速处于0.1-1.0 m/s范围内的振动响应。将圆柱体在不同流速下两向振动的CFD数值模拟与实验数据进行比较，得到了较为满意的结果。通过分析不同截面柱体在不同外流速下的振动幅值发现，带有抑振装置的柱体截面形式能够有效地减小涡激振动，其中，板状截面柱体抑振效果较好。

涡激振动；计算流体力学；两自由度；抑振

0 引 言

在海洋油气资源开发中，大量使用细长圆柱体管道结构，在海流、波浪等荷载作用下会产生涡旋脱落，使圆柱体结构发生涡激振动。当结构自振频率与旋涡脱落频率接近时，振动会迫使旋涡脱落频率固定在结构自振频率附近，发生频率锁定（lock－in）现象，引起圆柱体结构剧烈振动，目前工业上常用覆盖导流板或螺旋导板等抑振装置抑制圆柱体的涡激振动。

涡激振动的数值模拟目前主要有两种方法。一种是基于半经验方法，如现有计算软件MIT的SHEAR7和VIVARRAY等，另一种是基于计算流体力学（CFD）的数值模拟。半经验的数值模拟方法一般建立在大量实验得到的水动力系数数据库之上，而且大都只能计算圆柱体的涡激振动响应。对于带有抑振装置的不同截面形式柱体的涡激振动研究，只能依靠实验进行。CFD方法计算得到的流体参数较半经验方法更为准确，同时也能够模拟带有抑振装置的不同截面形式柱体的涡激振动响应。

用CFD方法模拟圆柱体的涡激振动，国内外的学者进行了大量研究。Guilmineau（2004）[1]讨论了低质量比圆柱体在湍流中的涡激振动响应，分别模拟了圆柱体在固定速度、变流速下的两自由度涡激振动。Namkoong（2005）[2]将流体方程与结构方程合并求解，模拟了层流状态下梁的振动响应。Prasanth与Mittal[3]模拟了低雷诺数下双圆柱涡激振动。分析得到不同约化速度下，前后圆柱的振幅与频率。万德成等人[4]使用Flunet软件，模拟得到圆柱体横向振荡运动，并成功模拟出尾流泄涡随振荡频率与振幅的变化。上述研究主要是针对二维圆柱体的流固耦合，对于不同截面形式柱体涡激振动的CFD模拟较少，徐枫（2006）[5]针对三角形、六边形等不同截面形状的柱体，进行横向涡激振动模拟，发现截面形式对柱体振动频率和振幅有较大影响。秦伟[12]建立了一种新的预报并列双圆柱涡激振动响应的经验性模型。根据特定间距比条件下旋涡脱落频率出现分支的现象，提出了以两个具有不同固有频率的尾流振子来共同描述结构的近壁尾涡动力特性。

本文将海洋立管简化为二维柱体结构，分别模拟圆柱体及带有抑振装置的不同截面形式柱体的两自由度涡激振动。计算中，主要考虑不同截面形式的涡激振动响应，同时观察不同流速下，不同截面形式柱体升力及结构振幅的变化。由于模拟的雷诺数较大，流体部分引入SST k-ω湍流模型，以便更加准确地模拟尾流的变化。结构部分采用无量纲方程，与流体部分联合求解，得到3种截面形式立管在不同流速下两自由度振动的振幅、频率、质心运动轨迹以及尾流变化模式。同时将数值模拟结果与Jauvtis和williamson（2004）[6]对质量比为m*=2.6的弹性支撑圆柱的涡激振动实验结果进行了比较与讨论。

1 数值模型

1.1 计算模型及参数

本文模拟的3种柱体形式为圆柱体，带有三角形导流板形式柱体（后简称带三角柱体），以及带有板型导流板形式的柱体（后简称带板柱体），其尺寸参数如表1所示。

表1 柱体尺寸参数（单位mm）Tab.1 The structural parameters of cylinders

本文简化模型为如图1（a）所示的弹簧—阻尼模型，计算流体区域为50D×20D（D为圆柱直径），其中尾流区域为42D（如图1（b））。为保证计算精度，柱体周围8D×8D为网格加密区，且1D范围内网格随柱体同步运动。图1（c）所示为带抑振装置柱体，在网格加密区内的几何模型细节图。柱体结构参数如表2所示，圆柱体在静水中的自振频率为5.0 Hz，外流速变化范围为0.1-1.0m/s。雷诺数变化范围为1 800～18 000。

表2 柱体结构参数Tab.2 The parameters of structure

图1 计算模型Fig.1 The computational models

1.2 控制方程

由于本文模拟的雷诺数较大，故流体部分在求解Navier-Stokes方程的基础上，引入SST k-ω湍流模型。结构部分，圆柱体运动控制方程为：

式中：m为圆柱体的质量，c为结构阻尼系数，k为结构刚度系数。Fx（t）、Fy（t）分别为顺流向和横向流体力：，其中σ为流体应力张量。

将结构位移，速度及加速度均无量纲化，（1）、（2）式可变为：

U为来流流速，Ur为约化速度，fn为结构在空气中的自振频率，为临界阻尼，CD、CL分别为结构阻力系数和升力系数。

1.3 计算流程

通过求解流体控制方程，提取不同流速下某一时刻柱体所受的流体作用力，将其代入结构控制方程（3）、（4），求得同一时刻结构与流体之间的相对位移和速度。根据结构相对速度，更新流体网格，稳定后进行下一时间步计算，循环求解直至预定时间步。

流体部分采用FLUENT软件求解，编写fsi-xy.c程序求解流体与结构耦合作用，计算流程如下：

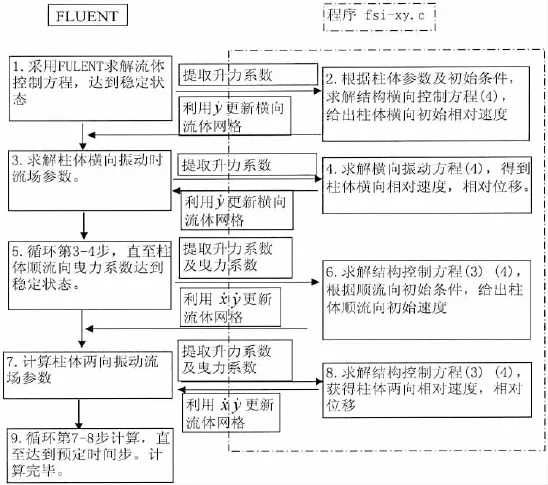
2 圆柱体的涡激振动

给定来流速度，使其约化速度在0.92-9.23范围内变化，按上述计算流程计算，可得柱体结构在不同流速下的振幅、升力与曳力系数以及振动频率，分别绘成图2、图3和图4。

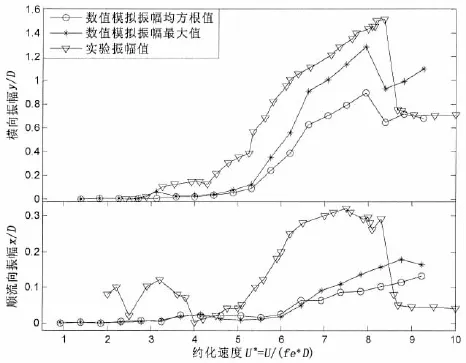
图2 不同流速下，对应圆柱体横向振幅y/D，顺流向振幅x/D与实验结果比较Fig.2 The dimensionless amplitude of cylinder at cross flow and in-line section compared with the experiment

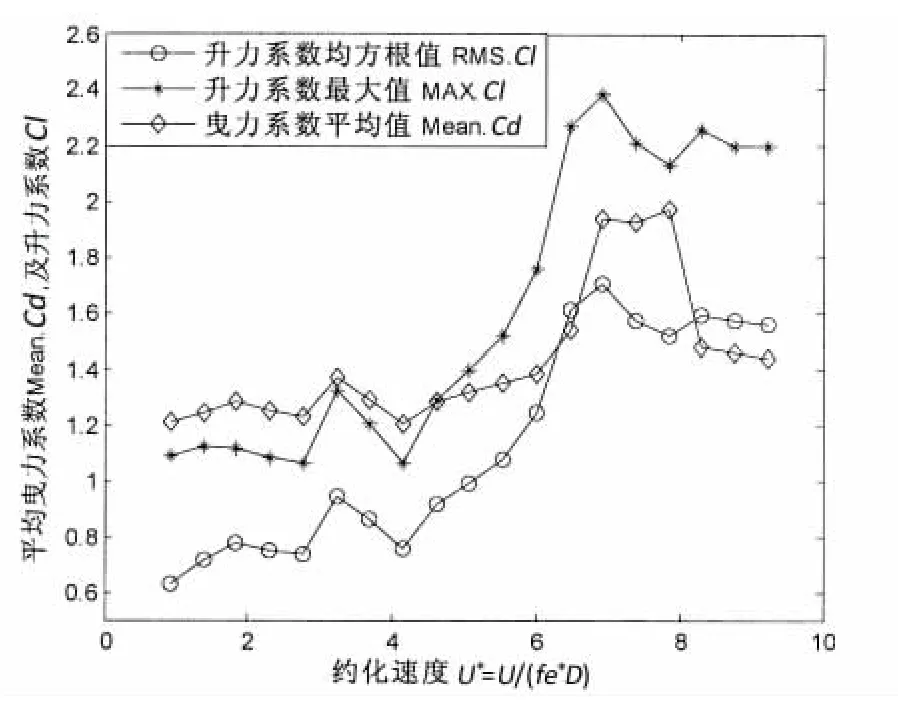
图3 不同流速下，圆柱体升力系数（RMS.y，MAX.y）与平均曳力系数Fig.3 The RMS.Cl and Mean Cd of circular cylinder

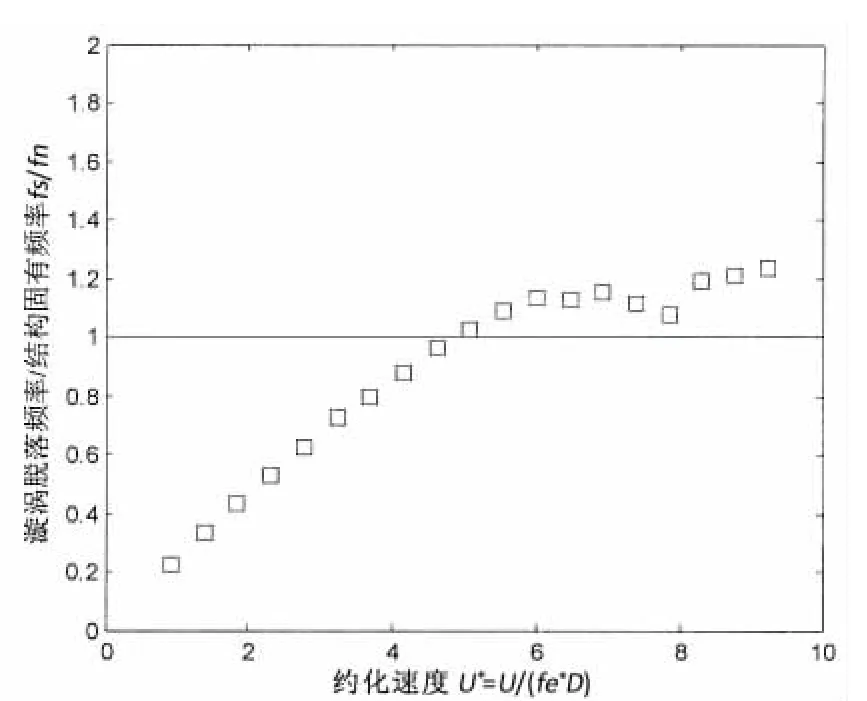
图4 不同流速下，圆柱体横向振动频率比Fig.4 The frequency ratio at cross-flow

由图2可以看出，随流速增加，柱体的振幅不断增大，圆柱体涡激振动发生锁振现象大约在Ur= 6.45之后；横向最大振幅为1.277 2，发生在Ur=7.84；顺流向最大振幅为0.2216，发生在Ur=9.23。将Jauvtis和Williamson[6]的实验数据绘入图2，发现实验中最大横向振幅1.5，最大顺流向振幅0.3，均发生在Ur=8.3时。经比较，本文计算得到的圆柱体涡激振动与实验结果基本相同，其振幅的变化趋势与实验基本一致，数值较实验结果略低。

图3中圆柱体的升/曳力系数变化趋势与图2类似，平均曳力最大值出现在Ur=7.84，而升力系数最大值出现在Ur=6.9。图4给出不同流速下漩涡脱落频率与结构自振频率比值，在Ur=5.08之后，其比值基本在fs/fn=1.0附近。计算中还发现柱体顺流向振动频率约为横向振动频率的2.0倍，与实验结果相符。

3 其他截面形式柱体涡激振动分析

利用圆柱体的计算方法，对带有抑振装置的不同截面形式柱体进行数值模拟。分别得到不同约化速度下，柱体升力、曳力系数，振动幅值的变化规律，并将其与圆柱体结果比较如图5、图6所示。

图5 不同流速下，各截面形式柱体的升力系数均方根值及曳力系数平均值Fig.5 The RMS.Cl and Mean Cd of cylinder with different cross-sections

3.1 升力系数与曳力系数

图5给出了不同截面形式的升力系数均方根值与平均曳力系数的变化规律。从图中可以看出，带三角柱体较圆柱体提前进入锁振阶段，达到锁振状态时，二者的最大升力系数的均方根值大致相等。其他状态下，带三角柱体的升力系数较圆柱体小。带板柱体升力系数的均方根值均小于圆柱体，其发生锁振时的约化速度与圆柱体基本相同。由于抑振装置改变了顺流向结构长度，使得带有抑振装置柱体曳力系数的平均值普遍小于圆柱体。

3.2 横向与顺流向振幅分析

图6中分别给出了不同流速下，不同截面柱体的振动幅值。由图可见，抑振装置的使用有效地抑制了柱体的横向振动，振幅明显降低。但对顺流向振动影响不大，且当带三角柱体达到锁振状态时，顺流向振幅大于圆柱体的顺流向振幅。带板柱体顺流向振动振幅较前二者偏低。两种带三角柱体对横向振动的抑振效果相差不大，而对于顺流向振动，尾翼为14 mm柱体的抑振效果优于尾翼为10 mm柱体。各截面形式柱体抑振比率为某流速下振幅减少量与圆柱体振幅之比，表3给出了各截面形式柱体平均抑振比率，其中负值表示其振幅大于圆柱体振幅。由图还可以看出，3种截面形式柱体达到锁振状态的时间及振幅变化趋势基本一致。

表3 各截面形式柱体平均抑振比Tab.3 The effective suppression ratio of cylinder with different cross-sections

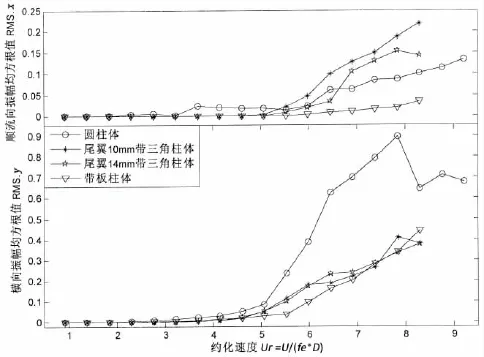
图6 不同流速下，各截面形式柱体振动幅值均方根值Fig.6 The amplitude of the cylinder with different cross-sections

3.3 典型流速下柱体响应特性

根据前面的分析，不同的截面形式对升力、曳力系数以及振动幅值均有影响。取Ur=5.53和Ur= 7.84作为典型流速，分析不同截面形式对柱体升力、曳力系数与振动幅值的影响（见图7）。同时给出每种截面形式柱体，在各自典型流速下的质心运动轨迹。

从图7中可以看出，当Ur=5.53时，3种柱体均未进入锁振状态（如图7（a））。由于三角形截面柱体已接近锁振状态，柱体振动受到其固有频率影响，曲线均表现出明显“差拍”现象。圆柱体时程曲线较为稳定，而带板柱体升力系数曲线发生明显偏移，且振幅很小。当Ur=7.84时，3种截面形式柱体均处在锁振状态下（如图7（b））。柱体振幅明显增大，振动频率锁定在固有频率附近。

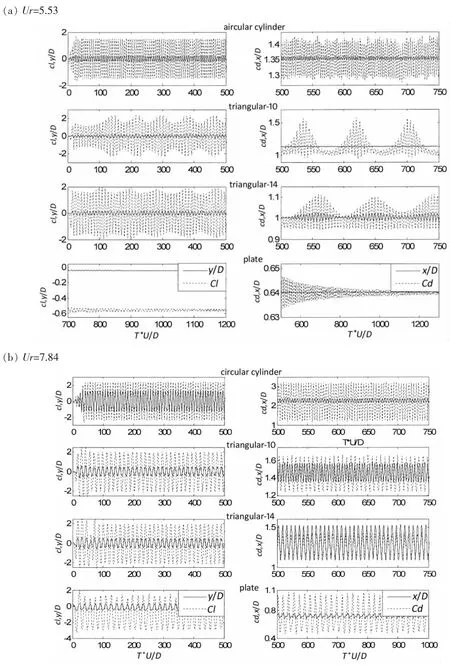
图7 Ur=5.33与Ur=7.84时，3种截面形式柱体升曳力系数与位移时程曲线Fig.7 The history of lift coefficient,drag coefficient and amplitude of cylinder with different cross-sections at different reduced velocity

此外，与其他三种截面形式柱体不同，带板柱体升力系数与横向的振幅平均值均为负值，即发生横向振动时，柱体脱离了原来平衡位置。这是由于板状导流板使得其后的区域产生压力突降，从而使尾流区域的压力零点上移，漩涡向外传播方向与来流方向产生了明显偏角，由此造成了板状柱体横向升力均值发生严重偏移，呈现明显的非对称性。

图8（a-d）给出了每种柱体在各自过渡状态和锁振状态下的质心运动轨迹。圆柱体及带三角柱体运动轨迹均呈现明显“8”字形状。表明，涡激振动是一种限幅振动。图8（a）中，当Ur=2.77和Ur=4.15时，圆柱体运动轨迹完全不同，表明柱体在低约化速度下，顺流向运动对柱体运动影响较大。从图8（b）、（c）中看出，当Ur=5.33和Ur=6.0时，由于“差拍”现象，带三角柱体振动未呈现标准正弦曲线，使其质心运动轨迹不规则，但仍能观察到“8”字形状。

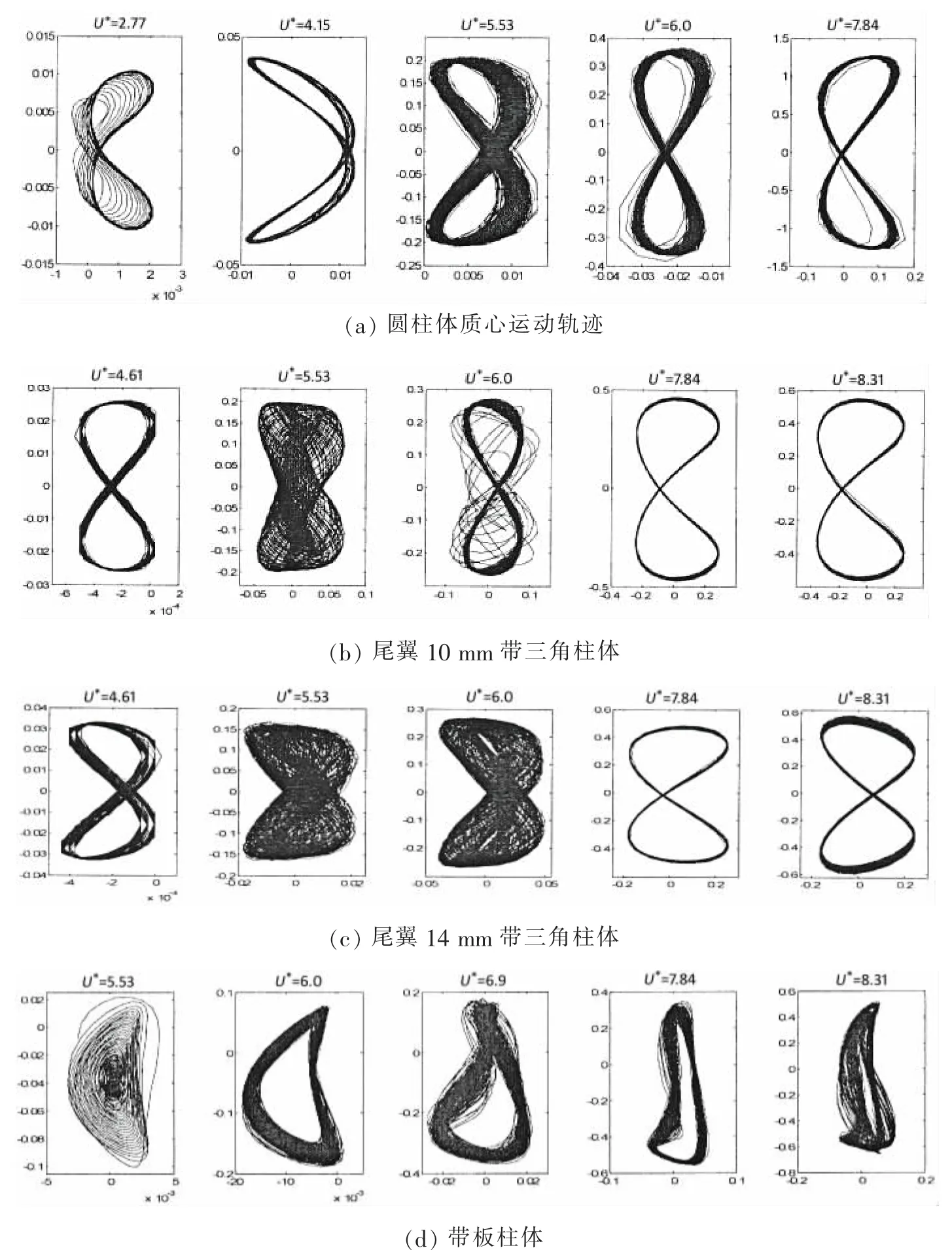
图8 各截面形式柱体在各自典型约化速度下的质心运动轨迹Fig.8 The x-y trajectory of cylinder with different cross-sections

带板柱体质心运动轨迹未呈现“8”字形状（如图8（d））。其原因主要是由于板状导流板不仅影响柱体横向振动，同时对顺流向振动振幅和频率都有较大影响。对板状截面导流板在典型流速下振幅进行傅里叶变化分析发现，柱体横向与顺流向振动包含频率个数也不相同。此外，从图中也能明显观察到，柱体横向振动的平衡位置为负。

4 结 论

本文采用CFD数值方法研究了不同截面弹性支撑柱体在不同流速下，两自由度涡激振动现象。通过计算，模拟出不同截面形式柱体振动振幅随流速变化的趋势，并观察到了锁振状态。同时发现带三角柱体较圆柱体提前进入锁振状态。带板柱体与圆柱体同时达到锁振。

通过模拟三角截面形式柱体两自由度振动情况，发现其能够有效减小柱体的横向振动，但增加了顺流向振动振幅。两者相比，尾翼14 mm的柱体抑振效果可达69.39%，优于尾翼为10 mm柱体，其抑振效果为67.95%。

带板柱体对横向与顺流向柱体振动均有较好的抑制作用。但由于板状导流板产生压力突降，使得柱体振动脱离原平衡位置，其横向振幅平均抑振率为87.51%。

综上可以看出，CFD方法可以针对不同截面形式柱体，计算其涡激振动响应。并且不同截面柱体对振动幅值有较大的影响，这对于圆柱体结构涡激振动抑振装置的研究，有较好的指导意义。

[1]Guilmineau E,Queutey P.Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow[J].Journal of Fluids and Structures,2004,19：449-466.

[2]Namkoong K,Choi H G,Yoo J Y.Computation of dynamic fluid-structure interaction in two-simensional laminar flows using combined formulation[J].Journal of Fluids and Structures,2005,20：51-69.

[3]Prasanth T K,Mittal S.Vortex-induced vibration of two circular cylinders at low Reynolds number[J].Journal of Fluids and Structures,2008.

[4]梁亮文,万德成.低雷诺数下二维圆柱涡激运动数值模拟[J].中国科技论文在线. Liang Liangwen,Wan Decheng.Numerical analysis of vortex-induced motion of a 2D circular cylinder in cross-flow with low reynolds numbers[J].Sciencepaper Online.

[5]徐 枫,欧进萍,肖仪清.不同截面形状柱体流致振动的CFD数值模拟[J].工程力学,2009,26(4)：7-15. Xu Feng,Ou Jinping,Xiao Yiqing.CFD numerical simulation of flow-induced vibration with different cross-section cylinder[J].Engineering Mechanics,2009,26(4)：7-15.

[6]Jauvtis N,Williamson C H K.Vortex-induced vibration of a cylinder with two degrees of freedom[J].Journal of Fluids and Structures,2003,17：1035-1042.

[7]Cunff C Le,Biolley F,Fontaine E,Étienne S,Facchinetti M L.Vortex-induced vibrations of risers：Theoretical,numerical and experimental investigation[J].Oil&Gas Science and Technology,2002,57(1)：59-69.

[8]Murakami S,Mochida A,Sakamoto S.CFD analysis of wind-structure interaction for oscillating square cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,72：33-46.

[9]Sun D,Owen J S,Wright N G.Application of the k-ω turbulence model for a wind-induced vibration study of 2D bluff bodies[J].Journal of Wind Engineering and Industrial Aerodynamics,2009,97：77-87.

[10]黄智勇,潘志远,崔维成.两向自由度低质量比圆柱体涡激振动的数值计算[J].船舶力学,2007,11(1)：1-9. Huang Zhiyong,Pan Zhiyuan,Cui Weicheng.Numerical simulation of VIV of a circular cylinder with two degrees of free-dom and tow mass-ratio[J].Journal of Ship Mechanics,2007,11(1)：1-9.

[11]陈文礼,李 惠.基于RANS的圆柱风致振动的CFD数值模拟[J].西安建筑科技大学学报,2006,38(4)：509-513. Chen Wenli,Li Hui.CFD numerical simulation of vortex-induced vibration of a circular cylinder based on a RANS method [J].Journal of Xi′an University of Architecture&Technology,2006,38(4)：509-513.

[12]秦 伟,康 庄.并列双圆柱涡激振动的经验性模型研究[J].海洋工程,2013,2(31)：11-18. Qin Wei,Kang Zhuang.Research on vortex-induced vibration of two side-by-side cylinders by using an empirical model[J].Ocean Engineering,2013,2(31)：11-18.

[13]尹纪富,尤云祥,李 巍.亚临界区雷诺数下圆柱绕流场电磁力控制数值研究[J].海洋工程,2014(4)：1-10. Yin Jifu,You Yunxiang,Li Wei.Numerical investigation of flow characteristics around a circular cylinder controlled by electromagnetic force at subcritical Reynolds numbers[J].Ocean Engineering,2014(4)：1-10.

Numerical simulation of VIV of cylinder with different cross-sections at two directions

ZHAO Jing,GUO Hai-yan
(College of Engineering,Ocean University of China,Qingdao 266071,China)

This paper focuses on the interaction between fluid and riser,i.e.,the flow field through forced oscillating cylinder with various cross-sections.Fluid-structure interaction(FSI)problems are solved by employing a combination of Computational Fluid Dynamics(CFD)numerical simulation and computational structural dynamics.Compared with a bare riser,the vibration pattern of risers equipped with various suppression devices is investigated to obtain their VIV characteristics.The results of numerical simulation by the present method is observed more close to the data of experiment.And it also shows that at the different flow velocity with the range between 0.1-1.0 m/s,the vibration amplitude of risers equipped with suppression devices is conspicuously smaller than that of the bare rise.Besides,the results show that the cylinder with plate suppression is the best performance.

Vortex-Induced Vibration;computational fluid dynamics;two degree of freedom;suppression

P75 O351.2

：Adoi：10.3969/j.issn.1007-7294.2016.05.003

1007-7294（2016）05-0530-10

2015-12-23

国家高技术研究发展计划项目（2010AA09Z303）；国家自然科学重点项目（50739004）；国家自然科学基金项目（51279187）

赵 婧（1983-），女，博士研究生，E-mail：mirror830@163.com；郭海燕（1959-），女，教授，博士生导师。