大深度潜器载人球壳开孔强度的理论计算及试验验证
2016-05-03李文跃欧阳吕伟李艳青沈允生
李文跃,欧阳吕伟,李艳青,沈允生,刘 涛,陈 鹏
(中国船舶科学研究中心深海载人装备国家重点实验室,江苏无锡214082)
大深度潜器载人球壳开孔强度的理论计算及试验验证
李文跃,欧阳吕伟,李艳青,沈允生,刘 涛,陈 鹏
(中国船舶科学研究中心深海载人装备国家重点实验室,江苏无锡214082)
文章根据外压球壳开孔区域的轴对称性和等面积补强所体现的主要强度特征对大深度载人厚球壳锥台形开口加强形式进行几何变换,同时求解系数十分复杂的三阶非齐次方程,完善和扩展球壳开口围壁、厚板嵌入组合加强的理论计算方法。通过两个4 500 m潜器球壳几种开口加强形式的应力集中系数理论计算、有限元计算和试验验证,证明了该方法的可靠性和适用性,可为制订大深度潜器载人球壳强度规范提供依据。
大深度潜器;载人球壳;开口强度;试验验证
0 引 言
壳体开孔强度计算在壳体理论上是十分复杂的,即使在一些工程应用中,包括潜艇、潜器、水下工程结构、压力容器等,采用某些假设进行近似计算也是十分繁琐的。因此,在我国潜器规范[1]中规定:承受外压力的球壳体开孔加强应采用直接计算法(有限元法)进行校核计算。大深度球壳由于承载安全性要求和材料的强度限制,一般都设计成中厚球壳(t/R=0.02~0.08),其开孔加强截面形式也有特殊的要求。为探讨这种球壳开口加强形式的结构强度计算方法,本文在应用文献[2]中基本理论方法基础上进行完善、扩展以及有限元计算,同时通过中厚度球壳(带有不同的开口半径和不同的加强形式)外压加载试验及应力测试验证这种解析分析方法的可靠性和其适用范围。
1 大深度潜器载人球壳开孔加强形式的几何变换
大深度潜器载人球壳开孔加强形式的设计应针对大深度载荷高屈强比材料、中厚度球壳等因素及使用上的要求进行优化设计。在结构形式上,应尽量避免薄壳围壁加强的突变形式,以减少开孔连接处表面应力峰值,有利于疲劳设计;在开口强度和承载能力方面则按等面积法加强原则进行等强设计,避免因强度不足而产生过高的一次应力,最大限度地保证完整球壳体受力形式不受局部开口影响;在使用上还应保证人孔的窗口盖密封可靠性、使用方便和观察窗的窗座刚度,如此等等。
对于壳体开孔加强,潜水器规范也有明确要求:应尽量避免采用腹板形式加强结构,有效的加强面积应不小于耐压壳体开孔部分需加强的截面积。也即等同于压力容器设计中的“等面积法”补强原则。
根据以上要求和设计原则,大深度载人球壳开口补强设计采用平滑过渡锥台截面的整环嵌入式与球壳开孔截面相接;根据使用要求,对于出入舱口采用外斜扇形锥台截面过渡形式(图1),对于观察窗为便于与有机玻璃窗镜安装采用内壁斜锥台截面形式(图2)。

图1 出入舱口Fig.1 Access hatch
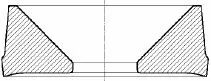
图2 观察窗Fig.2 View-port window
对于上述开口加强结构形式的解析分析和强度近似计算,在文献[2]中把加强构件视作一整圆环,利用环-球连接处的变形协调条件及边界系数的计算求解开孔边界的各应力集中系数。它的近似性在于假设图10中截面形式的整圆环为刚性,即环截面上任一点的位移等于环截面重心的位移,并认为环的宽度与开孔尺度相比可以忽略不计;而且由于球壳的基本微分方程已变换为一阶变态贝塞尔方程式,其解为零阶汤姆逊函数,具体计算非常复杂、收敛性差。
本文根据球壳开孔加强局部区域的完全轴对称性和等面积法补强在其强度计算中的主要体现是考虑开孔边缘的平均应力—整个截面的一次应力强度原则,将球壳加强的斜锥台截面形式依据截面积相等的方法进行几何变换成等厚度围壁(高度不变)和等厚度加强环(宽度不变)这样就可以利用文献[2]中球壳开孔围壁加强和围壁、厚板嵌入组合加强计算方法进行强度计算。由于在几何变换中,开口加强的主要参数包括开口半径、厚板加强宽度、围壁的高度及与壳板连接的位置和整个补强面积都保持不变。因而,计算结果(中面应力集中系数)能反映大深度载人球壳开口加强结构的主要强度特征,即变换后开口断面的中面应力(平均应力)状态基本保持不变。
通过进一步计算分析,开口加强形式几何变换中所涉及的两个变换参数:围壁厚度、加强环厚度,在其他开口加强结构各参数都不变的条件下,分别单独变换围壁的厚度δ和加强环板厚度h1,然后采用文献[2]中围壁加强理论方法和本文完善的围壁、厚板嵌入组合加强方法计算相应断面的应力集中系数。当δ和h1分别变化±20%情况下,应力集中系数变化很小,仅在5%以内。这说明所变换的参数对开口区的中面应力状态变化影响较小,也即说明该计算方法对中厚球壳的锥台形或扇形开口加强形式进行强度计算的适用性。
2 球壳开孔加强理论计算方法的完善
2.1 围壁加强的球壳开孔应力集中系数的计算方法
球壳开孔后采用围壁加强形式,如图3所示。
对于球壳的开较小口问题完全可视为一个轴对称问题。由文献[2]中壳体理论推导,球形扁壳在正交主曲率ρ、θ中的基本微分方程为:

式中:D为球壳抗弯刚度,R为球壳中面半径,h为球壳壳板厚度;p为静水压力,w为挠度函数,Φ为应力函数,Δ为算子
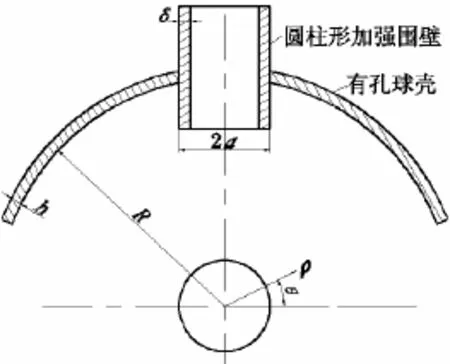
图3 开有围壁加强的圆形切口的球壳示意图Fig.3 Spherical shell with walls reinforcement circle opening
由(1)式可见,球壳开孔问题的求解最终归结为求解法向挠度w和应力函数Φ,由于w和Φ是耦合的,它们必须同时满足(1)式中的两个方程,即平衡方程和相容方程。如何求解两个联立的偏微分方程式是个比较复杂的问题。开孔壳体的试验研究表明,孔口区的高应力和变形是局部性的,随着离孔口距离增加而迅速衰减。从工程应用出发,文献[2]选择了一个近似方法,引入一些简化假定并设开孔球壳的挠度函数为一大指数衰减函数,即式中a为开孔半径,w为待定系数,可由壳体的变分方程式来确定。0

将挠度函数式(2)代入(1)式第二式,解得

式中:A、B为待定系数,根据孔边边界条件可以确定。
由上面近似处理后,位移函数w和应力函数Φ均为待定系数w0的函数,这样便可用一个方程式单独将应力函数解出。待定系数w0可应用能量法的混合变分方程进行积分求得,混合变分方程为
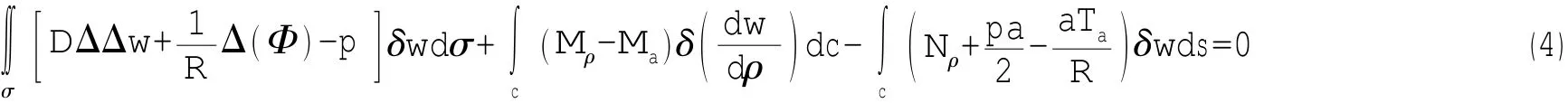
w0求得后,可求出应力函数Φ和挠度函数w,进而根据壳体物理方程求出相应的内力Tρ、Tθ和应力及球壳上任意一点的中面应力系数Kρ、Kθ。即
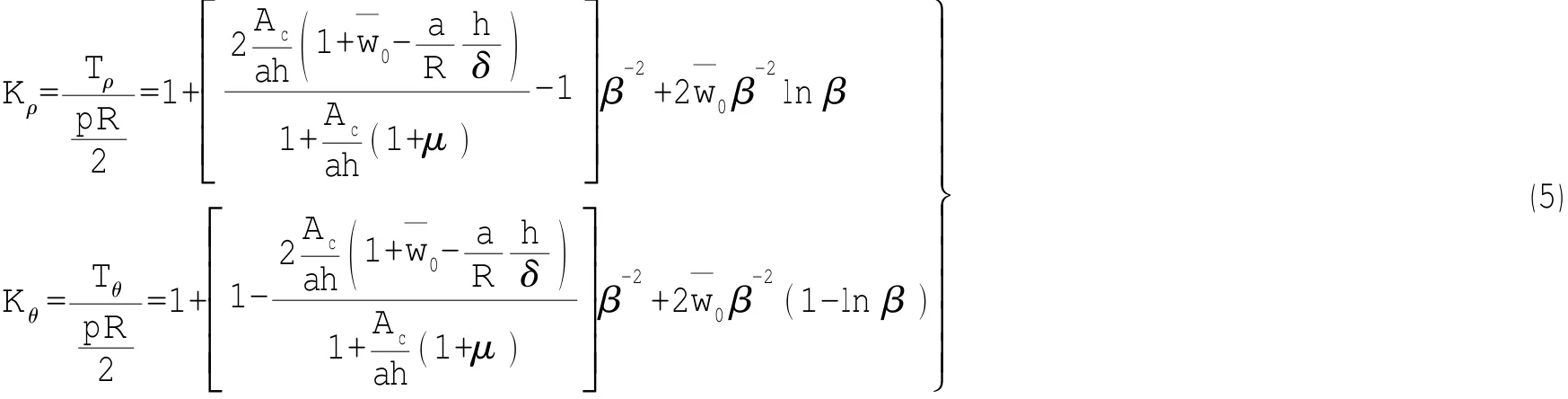
最大的中面应力系数发生在切口边缘处,即β=1处的周向应力系数Kθ,并记以(Kθ)max。

[2]的简化方法,对各参数简化处理后可得球壳开有围壁加强圆形切口的最大中面应力系数(Kθ)max的简化计算公式和图谱(图4)。

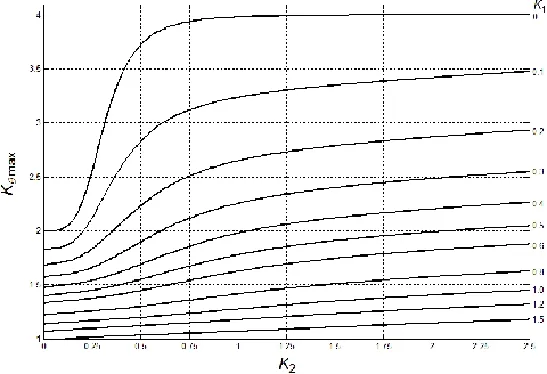
图4 球壳开有围壁加强的开孔应力集中系数Fig.4 Stress concentration factor of spherical shell with walls reinforcement
2.2 围壁、嵌入厚板组合加强的球壳开孔应力集中系数的计算方法的完善
球壳开孔组合加强的结构形式见图5。
对于采用围壁和嵌入厚板组合加强的球壳开孔,其求解原理和围壁加强的球壳开孔相类似,仅在厚、薄板交接处(ρ= b)增加了一个中面力的假定,同时也增加了一个位移连接条件。通过文献[3]的分析,组合加强的球壳开孔在孔口边缘(ρ= a)及厚、薄板交接处(ρ=b)会引起应力集中,它们的最大应力集中系数分别为ρ=a、ρ=b处的周向应力集中系数。由文献[3]中的计算推导分别得孔中边缘和厚、薄板交接处的应力集中系数的一般表达式,即
(1)嵌入厚板开孔边缘应力集中系数
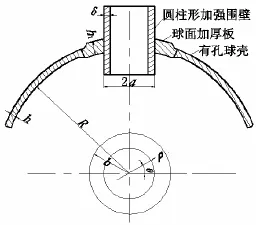
图5 球壳开孔组合加强结构示意图Fig.5 Spherical shell with wall and thick plate combination reinforcements
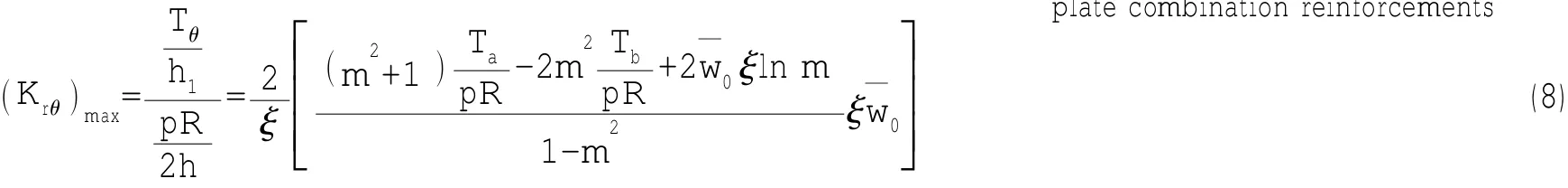
(2)厚壳板与薄壳板交接处球壳应力集中系数

组合加强的球壳开孔边缘上的最大应力集中系数可将一般表达式借助组合加强的圆柱壳同样的简化方法进行计算。对于厚、薄板交接处应力集中系数计算则需先求出一般表达式中的内力和位移显式。为此本文应用文献[3]中相应的方程和边界条件得出的三个参数方程,具体求解内力Tb和位移表达式w0,进而得出球壳厚、薄板交接处应力集中系数的计算公式。
①根据混合变分方程(4)求w0,可得
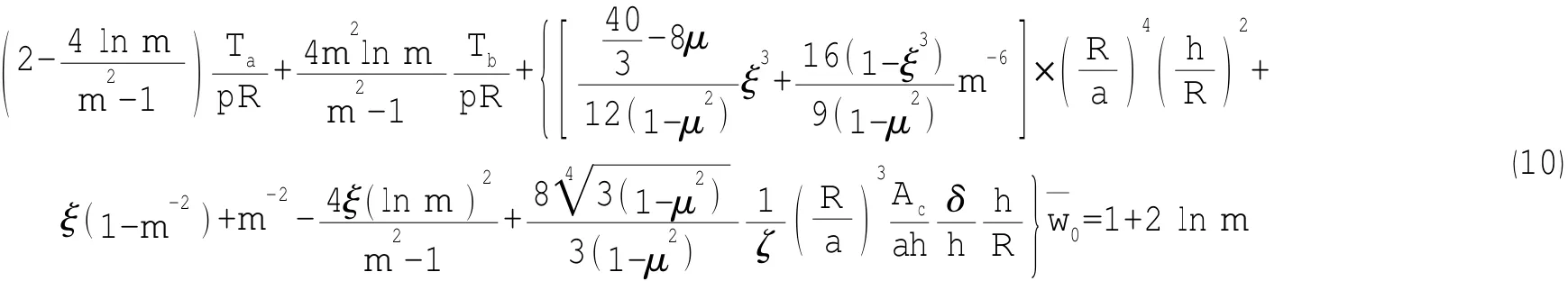
②根据加强围壁与球面嵌入厚板之间变形协调条件以及力的平衡条件可得
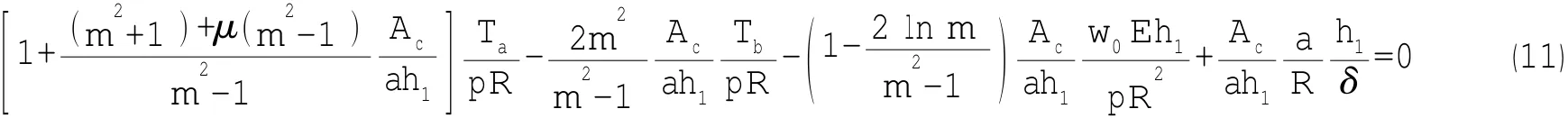
③根据球面嵌入厚板与球壳之间位移u相等的条件可得处应力集中系数表达式为
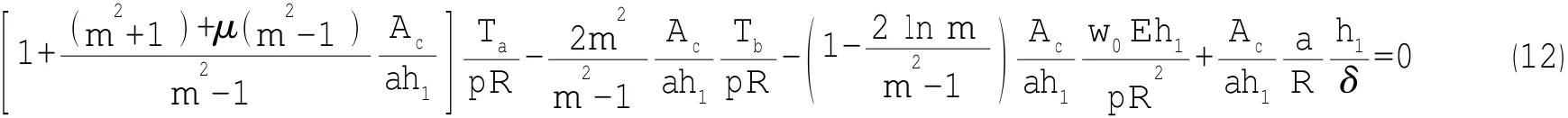
由①②③组成含有参数Ta、Tb、w0的方程组,本文求解该三阶非齐次方程组分别得出含有各种开口参数和系数的Tb、w0的具体表达式。若记则由(9)式可得出球壳厚、薄板交接

式中:
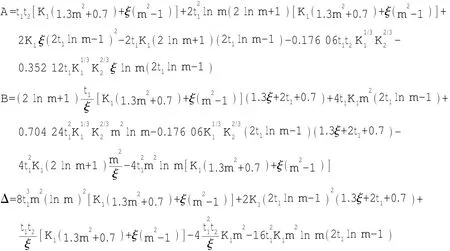

这样,在已知开口加强尺度参数条件下,计算围壁的有效高度和有效面积,进而根据(13)式计算厚、薄板交接处的最大应力集中系数(Ksθ)max。由于计算较繁琐,与围壁加强一样编制成相应图谱,即在已知m、ξ条件下,根据K1、K2的值查询系列图谱可得相应开口应力集中系数。如图6即为当m=1.5、ξ= 1.2时,根据上述应力集中系数计算结果绘制成的曲线族。
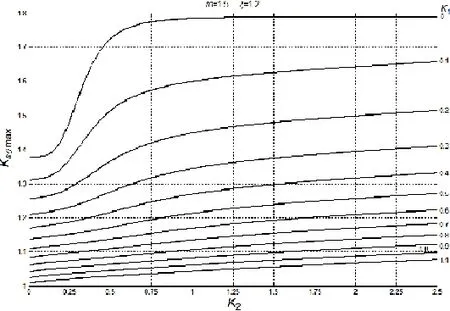
图6 某球壳开有围壁、厚板组合加强的开口应力集中系数Fig.6 Stress concentration factor of a spherical shell with wall and thick plate combination reinforcements
为检验(13)式的可靠性,对该式进行退化变换,即当m趋于1、ξ=1时,上述应力集中系数仍然可以表达为
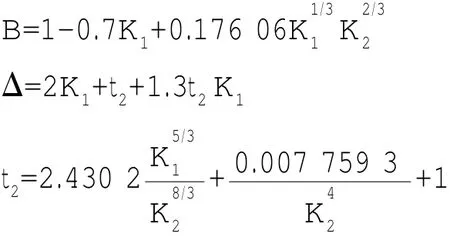
即退化为仅有围壁加强形式的计算公式,与公式(7)(用本文符号表达后)完全吻合,绘制的曲线也与图4完全一致。
3 载人球壳开口加强结构的应力集中系数计算
3.1 载人球壳的结构参数
本文结合4 500 m载人舱球壳(图7)结构设计所涉及出入舱口、主观察窗和前(舷)侧观察窗开口结构尺度进行具体计算。
载人舱球壳的主要技术参数[4]如下:
·材料:钛合金TC4ELI、Ti80
·内径:2 100 mm
·出入舱:开口半径330 mm
·主观察窗:开口半径315.7 mm
·前侧观察窗:开口半径262.9 mm
·舷侧观察窗:开口半径262.9 mm
3.2 观察窗开口加强应力集中系数计算
3.2.1 观察窗开口加强形式的变换
根据上述分析,首先将球壳各观察窗根据截面面积相等原则变换成相应的围壁加强形式,见图8,其中点P即为最大中面应力计算校核点。
3.2.2 观察窗围壁有效高度和有效面积的计算
根据变换后的相当围壁的高度和球壳连接位置计算围壁的有效高度和加强的有效面积,按文献[3]中计算步骤求解,其计算结果见表1。
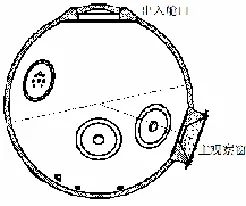
图7 载人舱球壳剖视图Fig.7 Section view of a spherical shell
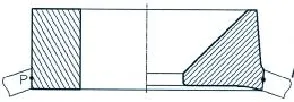
图8 观察窗开口加强变换形式Fig.8 Transformation form of a view-port window
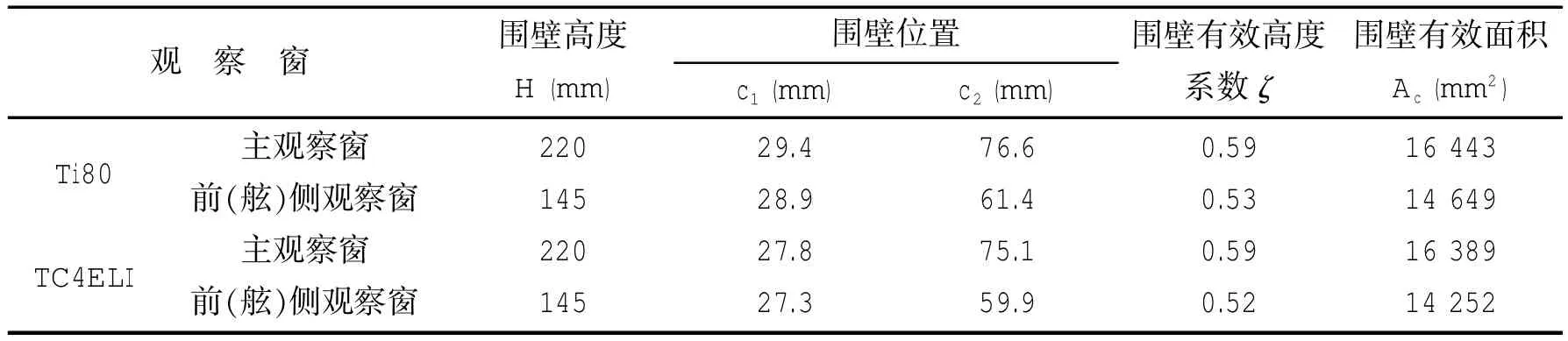
表1 观察窗围壁有效高度和有效面积计算结果Tab.1 Effective heights&areas of view-port window wall
3.2.3 应力集中系数的计算
根据转换后的几何参数和材料参数,计算应力集中系数,其结果见表2。
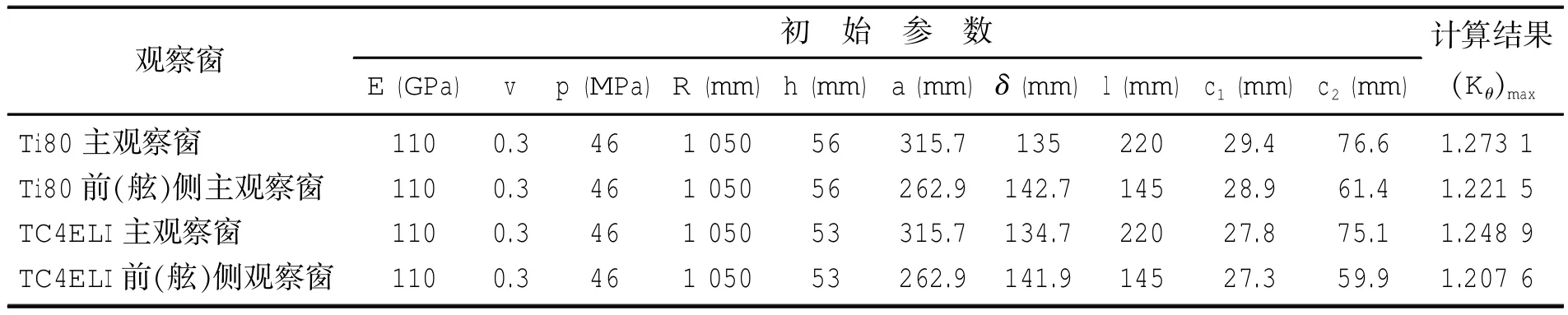
表2 观察窗开口加强应力集中系数计算结果Tab.2 Stress concentration factor results of view-port window
3.3 载人球壳出入舱口加强形式应力集中系数计算
3.3.1 出入舱口加强形式的变换
根据上述分析,首先将球壳出入舱口根据截面面积相等原则变换成相应的围壁、厚板嵌入组合加强形式,其计算断面为厚、薄板交接处,即图9点P1处。
3.3.2 围壁有效高度和有效面积的计算
根据变换后的相当围壁的高度和球壳连接位置计算围壁的有效高度和加强的有效面积,按文献[3]中计算步骤求解,其结果见表3。

图9 出入舱开口加强变换形式Fig.9 Transformation form of access hatch

表3 出入舱口围壁有效高度和有效面积计算结果Tab.3 Effective heights&areas of access hatch wall
3.3.3 应力集中系数的计算
根据转换后的几何参数和材料参数,计算最大应力集中系数,其结果见表4。

表4 出入舱开口加强应力集中系数计算结果Tab.4 Stress concentration factor results of access hatch
3.4 针对文献[2]中观察窗加强结构进行应力集中系数计算
文献[2]中潜水器观察窗模型的截面形式如图10所示,其结构尺寸见表5。

表5 文献[2]潜水器观察窗模型Tab.5 Parameters of a view-port window[2]
根据本文变换方法对该观察窗进行计算,可得加强构件与球壳交接处应力集中系数(Kθ)max=1.322 9,与文献中结果(Kθ)max=1.032 9相差较大。
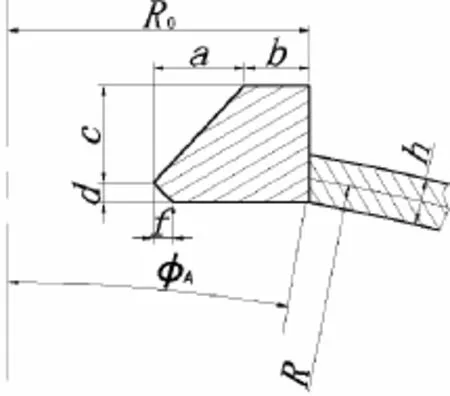
图10 某潜水器观察窗Fig.10 View-port window of a submersible
4 计算方法的试验验证
为验证4 500 m载人舱球壳的结构强度、承载能力和密封性,检验设计的合理性和加工制造质量,分别进行了两只球壳试验压力为46 MPa的外压试验,并在各开口部位和远离开口处的典型部位进行应力应变检测。开口部位的贴片如图11所示。

图11 开口部位应变片贴片图Fig.11 Strain gauge of opening areas
根据各开口区域所测得应变数据进行处理和计算,并与典型部位中面应力(平均应力)进行比较,得出开口区域实际的最大应力集中系数,见表6。
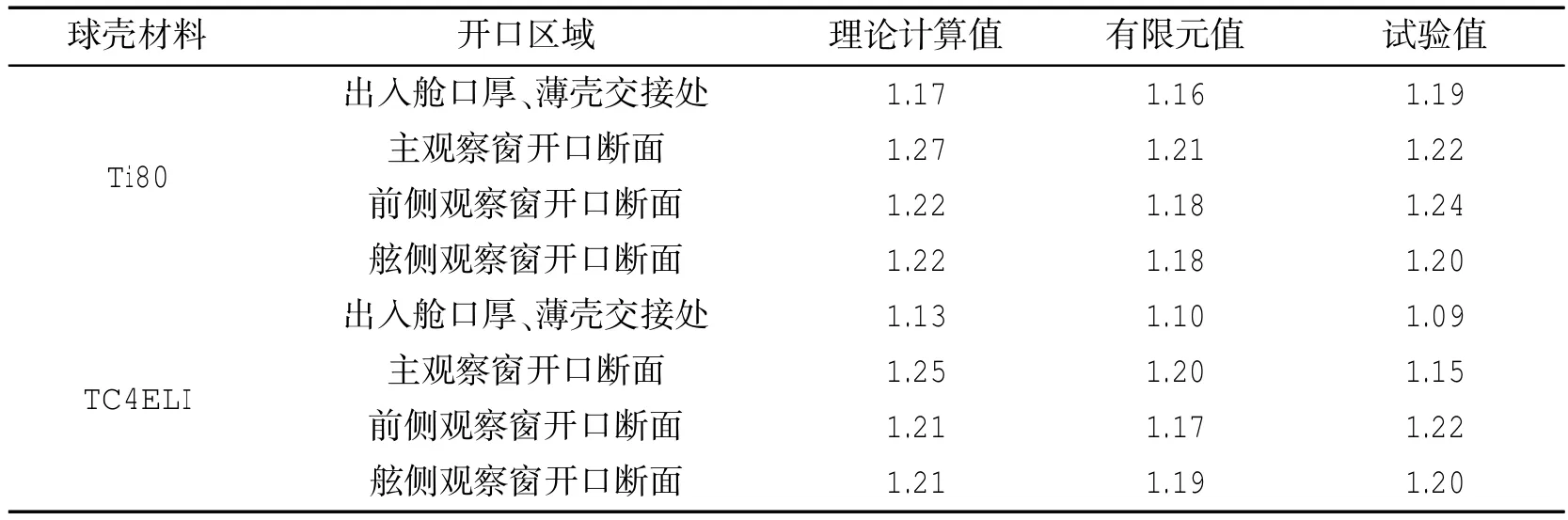
表6 开口区域应力集中系数理论计算结果及试验结果Tab.6 Theoretical calculations and experimental results of stress concentration factor
5 结 论
(1)为完善大深度潜器中厚度球壳开口加强结构的理论计算分析,本文采用等面积几何变换方法,将扇形、锥台形加强截面转变成围壁加强或围壁、厚板嵌入组合加强结构形式,通过理论计算、有限元计算和试验验证,在球壳开口区域采用等面积法加强的基本力学特征—一次中面应力没有产生明显的影响。因而,可以与潜器规范中的柱壳开口围壁加强一样地进行开口强度计算和应力校核。
(2)为建立大深度潜器出入舱口与球壳连接处的强度校核方法,本文在文献[2]中提出的一般表达式的基础上,通过联立求解系数十分复杂的三阶非齐次代数方程组建立了围壁、厚板嵌入组合加强结构与球壳连接处的应力集中系数的理论计算公式,并绘制了该位置处中面应力集中系数(Ksθ)max的曲线族。当m趋于1、ξ=1时,即与文献[2]中仅有围壁加强形式的计算公式和曲线完全一致。
(3)两只球壳的外压试验和测得的应力应变数据表明,开口加强区域应力最大部位发生在加强圆环与球壳开口连接处的外表面,甚至在经向出现较明显的峰值应力。
(4)表6应力集中系数的比较表明,大部分理论计算值与有限元计算结果、试验值吻合较好,相差在±5%以内。这说明将球壳开口锥台形加强截面变换成等厚度围壁及等厚度环板加强形式在开口区域一次应力强度的等效性。尽管4 500 m球壳的厚度半径比达0.05,已超出文献[2]中的一般范围(0.033),此时直法线假定和忽略法向应力的基本假定不完全适用,但通过计算分析,对于4 500 m球壳法向应力仅为中面应力的5%,而且应力集中系数是相对比较概念,因而该影响较小。此外,从球壳典型标准部位的各点应力试验数据得出的中面平均应力与按计算公式pR/2t得出的理论值十分接近,也可以说明该厚度半径比的影响是不大的。
(5)针对文献[2]中的观察窗截面形式和尺度(t/R=0.014),采用本文方法计算应力集中系数为1.322 9,而原文结果为1.032 9,两者相差较大。通过4 500 m球壳类似开口加强形式的观察窗试验结果和有限元分析表明,对于中厚度球壳而言本文方法相对合理和可信。
参考文献:
[1]中国船级社.潜水系统和潜水器入级与建造规范[S].北京:人民交通出版社,2013. CCS.Rules for the classification and construction of diving systems and submersibles[S].Beijing:China Communications Press,2013.
[2]徐秉汉,裴俊厚,朱邦俊.壳体开孔的理论与实验[M].北京:国防工业出版社,1987. Xu Binghan,Pei junhou,Zhu bangjun.Theory and experiments on shell opening[M].Beijing:National Defense Industry Press,1987.
[3]徐秉汉,朱邦俊,欧阳吕伟,裴俊厚.现代潜艇结构强度的理论与试验[M].北京:国防工业出版社,2007. Xu Binghan,Zhu bangjun,Ouyang lvwei,Peijunhou.Theory and experiments on modern submarine structure strength[M]. Beijing:National Defense Industry Press,2007.
[4]沈允生.4500米载人潜水器载人舱球壳设计计算报告[R].无锡:中国船舶科学研究中心,2014. Shen Yunsheng.Calculation report of 4 500 m HOV manned cabin spherical shell design[R].Wuxi:CSSRC,2014.
[5]陈 鹏.Ti80/TC4ELI载人舱球壳静水外压试验检测报告[R].无锡:中国船舶科学研究中心,2015. Chen Peng.Test report of Ti80/TC4ELI manned cabin spherical shell under external pressure[R].Wuxi:CSSRC,2015.
Theoretical calculation and experimental verification for opening strength of deep manned spherical shell
LI Wen-yue,OUYANG Lv-wei,LI Yan-qing,SHEN Yun-sheng,LIU Tao,CHEN Peng
(State Key Laboratory of Deep-sea Manned Vehicles,China Ship Scientific Research Center,Wuxi 214082,China)
According to the axial symmetry of external pressure spherical shell open areas and strength characteristics of Equivalent Area Reinforcement,this paper makes geometric transformations to cone-platformed open reinforcements of deep manned thick spherical shell and solves a complicated three-order nonhomogeneous equation,perfecting and expanding theoretical calculation methods of spherical shell opening with wall and thick plate combination reinforcements.Based on the theoretical calculation,FEM and experimental verification of stress concentration factor in two 4 500 meters deep manned spherical shells,the reliability and applicability of this method is proved.This paper can provide basis for revising deep-sea manned spherical shell strength specification.
deep submersible;manned spherical shell;opening strength;experimental verification
U662
:A
10.3969/j.issn.1007-7294.2016.10.009
1007-7294(2016)10-1289-10
2016-07-25
国家高技术研究发展计划(863计划)课题(2014AA09A110)
李文跃(1989-),女,硕士研究生,工程师,E-mail:821682118@qq.com;欧阳吕伟(1941-),男,研究员。
