疏水表面流体流动特性的格子Boltzmann方法模拟

黄桥高，潘 光

（西北工业大学航海学院，西安710072）

疏水表面流体流动特性的格子Boltzmann方法模拟

黄桥高，潘 光

（西北工业大学航海学院，西安710072）

采用格子Boltzmann方法研究了微形貌对固体表面润湿性的影响，在此基础上进一步模拟了具有微形貌的疏水表面通道内的流体流动，从法向速度、剪应力、滑移速度等角度分析了疏水表面的流场特性，揭示了疏水表面滑移流动的产生机制。结果表明，疏水表面的滑移流动是由低表面能作用和微形貌共同引起的。具有微形貌的疏水表面比光滑疏水表面具有更好的减阻效果，原因在于微形貌能够驻留气体，形成的气液自由剪切面加剧了疏水表面的滑移流动，最大滑移速度可以达到主流平均速度的50%左右。

疏水表面；格子Boltzmann方法；微形貌；滑移流动；减阻

0 引 言

在经典宏观流体力学的教科书和科技论文中，几乎都有一个相同的假设：在固体和流体的交界面上没有滑移，即固体和流体在交界面上没有相对运动，这就是所谓的无滑移边界条件。但是对于微纳米尺度流动，系统极大的面体比使得表面属性成为影响流动的主导因素，即使是流体在固体壁面纳米量级的滑移也会给流体输运带来重要影响[1-2]。疏水表面的减阻作用就是由这种滑移效应引起的[3-6]。

疏水表面上的滑移流动现象已在诸多实验中被证实。Balasubramanian[7]采用PIV技术对附有人工疏水涂层的玻璃平板进行了流场测试，发现在硬件设备所能分辨的最靠近平板壁面处，流体速度不为零，即产生了滑移。Ou[8]采用μ-PIV技术对疏水表面流体流动进行了速度测量，在疏水表面微形貌的气液界面上观察到了滑移流动，最大滑移速度约为20 μm/s，达到主流平均速度的50%。数值模拟方面，陈艳燕[9]、黄桥高[10]等均采用格子Boltzmann方法对疏水表面流体流动特性进行了研究，证明了无滑移边界条件能够产生表观滑移，并指出滑移流动主要受流体与固体壁面之间相互作用强度的影响。但他们的研究是针对光滑疏水表面而言的，只考虑了材料属性对滑移流动的影响，并未体现微形貌的作用，所以获得的最大滑移速度仅为主流平均速度的10%左右，与Ou的实验测试结果有较大出入。本文采用格子Boltzmann方法对具有微形貌的疏水表面的流体流动进行数值模拟，分析疏水表面的流场特性，揭示材料属性和微形貌对疏水表面滑移流动的影响机制。

1 具有微形貌的疏水表面润湿性模拟

文献[10]基于格子Boltzmann方法对光滑疏水表面的润湿性进行了数值模拟，但众所周知，疏水表面的润湿性主要由材料属性和微形貌共同决定。本文在文献[10]的基础上，考虑微形貌的作用，模拟了实际疏水表面的润湿性。关于格子Boltzmann方法、Shan-Chen模型以及光滑疏水表面的润湿性模拟参见文献[10]，此处不赘述。

在具有微形貌的疏水表面润湿性模拟中，以二维方柱代表疏水表面的粗糙单元，其几何尺寸分别为柱的宽度a，柱的间距b和柱的高度h。图1是计算稳定后三种不同结构表面上的液滴形态，计算中取相同的吸附参数Gs=-2.4，即假设各表面的材料属性相同。从图中可以发现液滴在光滑疏水表面上的接触角为108.9°，其疏水性较弱；对光滑疏水表面进行粗糙化处理后，其疏水性显著增强。当复合接触面上气液界面分数fv=b/（a+b）=0.333时，表观接触角为123.1°；当fv=0.667时，表观接触角为139.7°。此外，根据Cassie-Baxter润湿状态方程cosθCB=（1- fv）cosθY-fv可以计算出本征接触角θY= 108.9°、气液界面分数fv=0.333和fv=0.667时疏水表面的表观接触角分别为123.3°、140.8°。数值模拟结果与理论预测值非常接近，证明本文的方法能够较准确地模拟具有微形貌的疏水表面的润湿性。

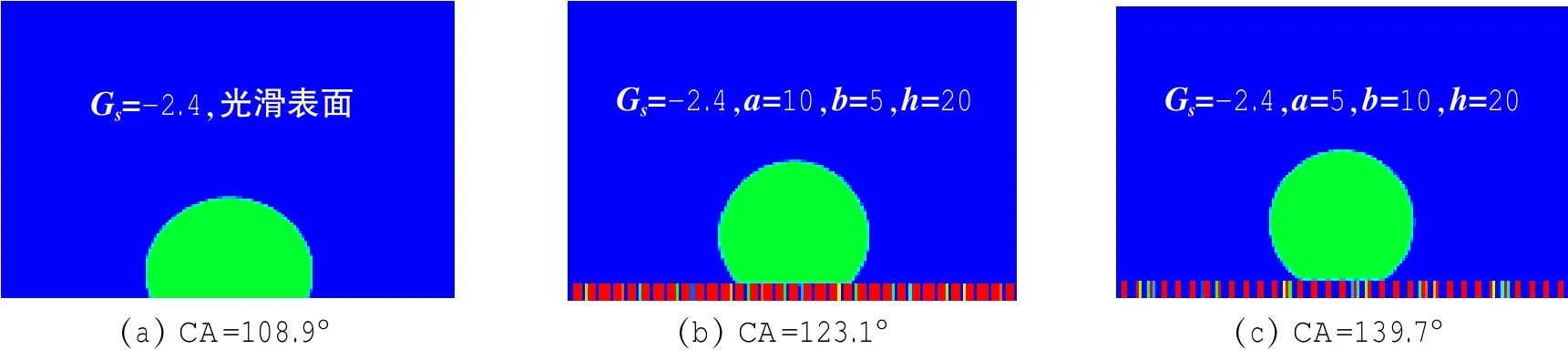
图1 不同结构表面上液滴的形态及表观接触角值Fig.1 Droplet shape and apparent contact angle of different hydrophobic surfaces

2 疏水表面流体流动特性数值模拟

已有的实验研究表明，液体流过疏水表面时，在其微形貌内会驻留一部分气体从而形成气液自由剪切面[14-15]。因此，气液两相流流动是疏水表面流场和普通无滑移表面流场的最大差别，可以以此为依据设置数值计算模型的初始条件。如图2所示，假设初始状态时疏水表面微形貌的凹槽内充满气体，即气液自由剪切面为一条与凹槽顶部平齐的直线，图中蓝色区域、绿色区域、红色区域分别表示气体、液体、固体和液体在压力梯度驱动下沿通道x方向流动。计算区域为121×221格子单位的矩形通道，左右边界采用周期性边界格式，上下壁面采用无滑移反弹格式。通道的上壁面为光滑表面，下壁面为具有微形貌的疏水表面，其本征接触角为108.9°和120.5°（即吸附参数Gs=-2.4和Gs=-2.0），微形貌的几何尺寸为a=10，b=20，h=20和a=10，b=30，h=20。

图3是不同表面通道的流体平均速度图。当流动稳定后，相对于普通无滑移表面通道，四种疏水表面通道的流体平均速度显著增大，增幅分别为4.75%、8.98%、11.19%和15.69%，说明疏水表面具有一定的减阻作用，而且本征接触角越大、气液自由剪切面越长，通道的流体平均速度越大，减阻效果越明显。对比文献[10]的模拟结果可以发现，相同材料属性的情况下，具有微形貌的疏水表面通道的流体平均速度比光滑疏水表面通道的流体平均速度要大，即微形貌进一步提高了疏水表面的减阻效果。

图2 疏水表面流体流动的初始状态Fig.2 The initial state of hydrophobic surfaces’liquid flow

图3 通道的流体平均速度Fig.3 Mean velocity of different hydrophobic surfaces

图4 疏水性表面速度分布云图Fig.4 Velocity contours of different hydrophobic surfaces

图4为具有微形貌的疏水表面的流场速度分布云图。从整体上看，疏水表面的流场速度分布与普通无滑移表面相似，表明微形貌的存在并未扰乱流场的整体分层结构，其影响仅限于近壁区。

下面将详细给出疏水表面近壁区不同位置处的法向速度分布情况，图5为各速度测量点位置示意图，图6、图7分别为疏水表面微形貌肋台面上和凹坑内不同位置处的速度分布曲线。与普通无滑移表面相比，疏水表面近壁区的速度分布曲线出现了明显的上抬现象，其原因有二：低表面能作用（代表材料属性）在近壁区诱导了一个低密度层，在低密度层上发生了表观滑移（文献[10]基于光滑疏水表面流体流动特性获得的结论）；微形貌促使了气液自由剪切面的形成，流体在气液自由剪切面上也发生了滑移。同时，微形貌凹坑内速度出现了负值，间接表明微形貌内存在漩涡。

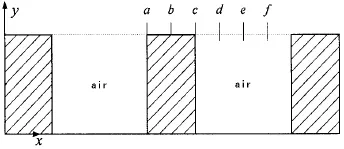
图5 疏水表面速度测量点位置示意图Fig.5 Schematic of the each measurement point location on hydrophobic surfaces

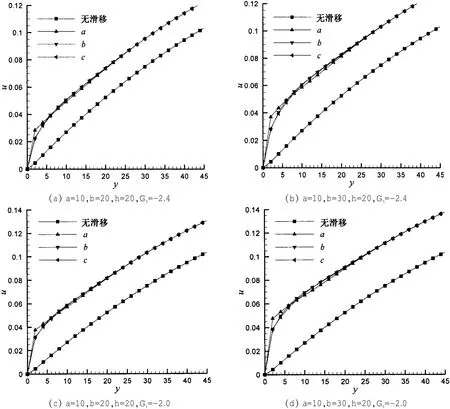
图6 微形貌肋台面上不同位置处速度分布图Fig.6 Velocity distribution on rib table at different locations

图8、图9分别为疏水表面微形貌肋台面上和凹坑内的剪应力分布曲线图。在肋台面上，剪应力沿流动方向呈逐渐降低的趋势，即迎流面的剪应力较大，背流面的剪应力较小。从图7所示的肋台面上不同位置处速度分布曲线可以看出，a位置的速度曲线上抬最明显，然后依次为b和c，由于各位置处壁面速度仍为零，因此，上抬越明显，则速度梯度越大，剪应力也就越大，这与剪应力分布曲线图反映出的结果一致。在凹坑下壁面上，剪应力几乎呈对称分布，即中间大部分区域的剪应力为零，两个底角附近的剪应力大小相等，方向相反，这说明凹坑内两个底角附近存在旋向相反的漩涡，且凹坑下壁面的剪应力合力近似为零。

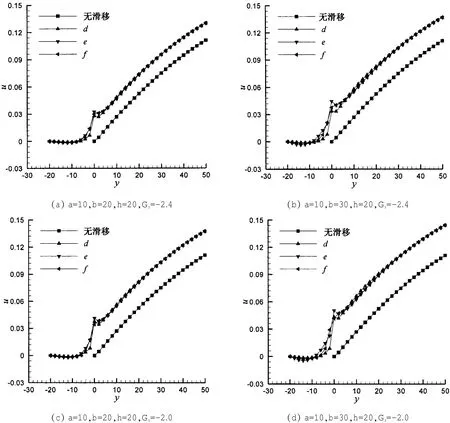
图7 微形貌凹坑内不同位置处速度分布图Fig.7 Velocity distribution within the pit at different locations

图8 微形貌肋台面上剪应力分布图Fig.8 Shear stress distribution on rib table at different locations

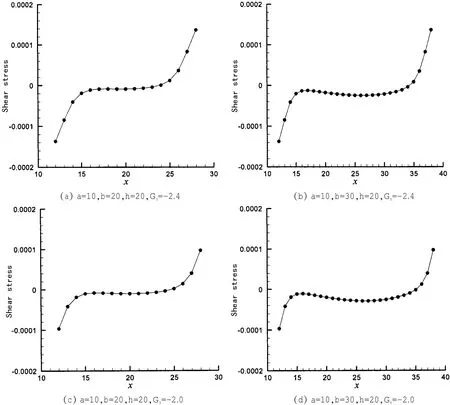
图9 微形貌凹坑内剪应力分布图Fig.9 Shear stress distribution within the pit at different locations

图10为疏水表面气液自由剪切面上的速度分布曲线。从图中可以看出，气液自由剪切面上的流体速度均不为零，即发生了滑移流动，而且滑移速度沿流动方向存在先增大后减小的趋势，最大值出现在交界面中点靠下游的地方，过了最大值点后，滑移速度有陡降的现象出现。这是因为对于具有微形貌的疏水表面，气液自由剪切面与肋台面在流动方向上交错分布，气液自由剪切面有增大滑移的作用，滑移速度沿流动方向本应越来越大，但在接近肋台面时，受其无滑移流动的限制，滑移速度急剧减小。另外，随着气液自由剪切面变长，最大滑移速度也在增大，如b=20时两种疏水表面（对应的本征接触角为108.9°、120.5°）的最大滑移速度分别为0.032 7、0.040 6，约为主流平均速度的32%、37%，而b= 30时两种疏水表面的最大滑移速度分别为0.045 2、0.056 3，约为主流平均速度的42%、49%。可见，疏水表面的本征接触角越大、气液自由剪切面越长，则最大滑移速度越大。对比文献[10]的模拟结果可以发现，合适尺寸的微形貌能够驻留气体从而形成气液自由剪切面，加剧了疏水表面的滑移流动。

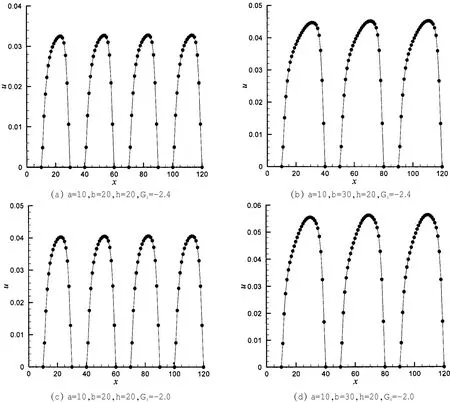
图10 疏水表面气液自由剪切面处速度分布图Fig.10 Velocity distribution on gas-liquid interface of different hydrophobic surfaces

3 结 论

本文利用格子Boltzmann方法对疏水表面的流体流动进行数值模拟，从法向速度、剪应力、滑移速度等角度分析了疏水表面的流场特性，获得如下结论：

（1）疏水表面的滑移流动是由低表面能作用和微形貌共同引起的，这是疏水表面具有减阻作用的直接原因。

（2）具有微形貌的疏水表面比光滑疏水表面具有更好的减阻效果，而且本征接触角越大、气液自由剪切面越长，疏水表面的减阻效果越好。

（3）单一的低表面能作用仅能产生小量滑移，最大滑移速度仅为主流平均速度的10%左右；在光滑疏水表面上构筑微形貌，能够驻留气体从而形成气液自由剪切面，加剧了疏水表面的滑移流动，最大滑移速度能够达到主流平均速度的50%左右，最终表现出显著的减阻效果。

[1]徐 超,何雅玲,王 勇.纳米通道滑移流动的分子动力学模拟研究[J].工程热物理学报,2005,26(6):912-914. Xu Chao,He Yaling,Wang Yong.Molecular dynamics studies of velocity slip phenomena in a nanochannel[J].Journal of Engineering Thermophysics,2005,26(6):912-914.

[2]曹炳阳,陈 民,过增元.纳米通道内液体流动的滑移现象[J].物理学报,2006,55(10):5305-5310. Cao Bingyang,Chen Min,Guo Zengyuan.Velocity slip of liquid flow in nanochannels[J].Acta Physica Sinica,2006,55 (10):5305-5310.

[3]Choi C H,Kim C J.Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface[J].Physical Review Letters,2006,96(6):066001(1-4).

[4]Choi C H,Ulmanella U,Kim J,et al.Effective slip and friction reduction in nanograted superhydrophobic microchannels [J].Physics of Fluids,2006,18(8):087105(1-8).

[5]Ou J,Perot B,Rothstein J P.Laminar drag reduction in microchannels using ultrahydrophobic surfaces[J].Physics of Fluids,2004,16(12):4635-4643.

[6]Zhang R L,Di Q F,Wang X L,et al.Numerical study of the relationship between apparent slip length and contact angle by lattice Boltzmann method[J].Journal of Hydrodynamics,2012,24(4):535-540.

[7]Balasubramanian A K,Miller A C,Rediniotis O K.Microstructured hydrophobic skin for hydrodynamic drag reduction[J]. AIAA Journal,2004,42(2):411-414.

[8]Ou J,Rothstein J P.Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces[J].Physics of Fluids,2005,17(10):103606(1-10).

[9]Chen Y Y,Yi H H,Li H B.Boundary slip and surface interaction:A lattice Boltzmann simulation[J].Chinese Physics Letters,2008,25(1):184-187.

[10]黄桥高,潘 光,宋保维.疏水表面滑移流动及减阻特性的格子Boltzmann方法模拟[J].物理学报,2014,63(5): 054701(1-7). Huang Qiaogao,Pan Guang,Song Baowei.Lattice Boltzmann simulation of slip flow and drag reduction characteristics of hydrophobic surfaces[J].Acta Physica Sinica,2014,63(5):054701(1-7).

[11]Bhatnagar P L,Gross E P,Krook M.A model for collision processes in gases.I.Small amplitude processes in charged and neutral one-component systems[J].Physical Review,1954,94(3):511-525.

[12]Shan X W,Chen H D.Lattice Boltzmann model for simulating flows with multiple phases and components[J].Physical Review E,1993,47(3):1815-1819.

[13]Shan X W,Chen H D.Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation[J]. Physical Review E,1994,49(4):2941-2948.

[14]Min T,Kim J.Effects of hydrophobic surface on skin-friction drag[J].Physics of Fluids,2004,16(7):55-58.

[15]McHale G,Shirtcliffe N J,Evans C R,et al.Terminal velocity and drag reduction measurements on superhydrophobic spheres[J].Applied Physics Letters,2009,94(6):064104(1-3).

Lattice Boltzmann simulation of liquid flow characteristics of hydrophobic surfaces

HUANG Qiao-gao,PAN Guang
(School of Marine Science and Technology,Northwestern Polytechnical University,Xi'an 710072,China)

The influence of microcosmic topography on the surface wettability is investigated using a lattice Boltzmann method,and then the liquid flow over hydrophobic surfaces with microcosmic topography is simulated in a microchannel.From aspect of normal velocity,shear stress and slip velocity,the flow field characteristics of hydrophobic surfaces are analyzed and the generation mechanism of hydrophobic surfaces’slip flow is revealed.The simulation results show that hydrophobic surfaces’slip flow is caused by the low surface energy effect and microcosmic topography together.Hydrophobic surfaces with microcosmic topography have a better drag reduction effect than smooth hydrophobic surfaces.The reason is that the microcosmic topography can retain gas and generate gas-liquid free shear surfaces,which can enhance hydrophobic surfaces’slip flow and make the maximum slip velocity reach about 50%of the average speed of mainstream.

hydrophobic surface;lattice Boltzmann method;microcosmic topography;slip flow; drag reduction

O357.5

：A

10.3969/j.issn.1007-7294.2016.10.001

1007-7294（2016）10-1211-08

2016-05-14

国家自然科学基金（51279165，51109178）；教育部高等学校博士学科点科研基金（20126102120021）

黄桥高（1983-），男，讲师，E-mail:huangqiaogao@163.com；潘 光（1969-），男，教授，博士生导师。