大型油船和散货船波激振动及其对结构疲劳寿命的影响

杨 鹏，顾学康，丁 军，张 凡，胡嘉骏

（1.武汉第二船舶设计研究所，武汉430205；2.中国船舶科学研究中心，江苏无锡214082）

大型油船和散货船波激振动及其对结构疲劳寿命的影响

杨 鹏1，2，顾学康2，丁 军2，张 凡2，胡嘉骏2

（1.武汉第二船舶设计研究所，武汉430205；2.中国船舶科学研究中心，江苏无锡214082）

通过一艘大型油船和一艘大型散货船在水池中的波激振动模型试验，研究了规则波和不规则波中的船体波激振动现象，利用试验获得的短期海况下的高低频应力数据计算分析了波激振动对实船典型结构疲劳损伤的影响。在此基础上，通过对试验数据的规律性研究，提出了一种快速估算短期海况中船体波激振动特征及其对结构疲劳寿命影响的方法。利用该方法，结合几条典型航线的长期海况统计资料，研究了不同航线上船体波激振动对结构疲劳寿命的影响。研究结果认为：大型油船和散货船在压载状态下存在明显的波激振动现象，不同航线上的波激振动强度及其对结构疲劳寿命的影响差别较大；快速估算方法能够合理地评估船体在波激振动下的结构疲劳损伤，具有一定的工程实用价值。

油船；散货船；波激振动；模型试验；疲劳损伤

0 引 言

传统船舶由于船体梁二节点固有振动频率远远高于波浪载荷激励频率，因此波激振动不明显。随着船舶结构主尺度的不断增大，同时高强度钢的广泛应用，船舶结构物在海洋环境下显得越来越具有弹性，流固耦合现象变得越来越明显。随着船体梁刚度的降低，船体二节点振动频率会位于波浪激励载荷主要频率区间内，因此会产生明显的波激振动现象（Storhaug（2007）[1]；Wu和Moan（2007）[2]；Lijima等（2008）[3]；Pedersen和Jensen（2009）[4]；汪雪良等（2012）[5]）。船体结构的高频波激振动会增加船体结构应力响应幅值和循环次数，对于某些船型会产生十分严重的疲劳问题[1，6-7]，例如DNV的一艘25万吨大型矿砂船[1]。近几年来的研究表明船体二节点垂向波浪诱导高频振动会对船体结构疲劳破坏产生相当大的贡献，例如Storhaug等[6]对一长294 m（Lpp）的矿砂船在北大西洋航线上航行的实船测量就表明了这一点。Drummen等[7]对一艘集装箱船在顶浪中由波浪诱导振动产生的疲劳损伤进行了模型试验和数值计算研究，测量的结果表明波浪诱导振动产生约40%的总疲劳损伤。数值方法对波频损伤预报较好，但对总疲劳损伤的预报偏大，达到了50%。近年来IACS（国际船级社组织）在最新的HCSR[8]（油船和散货船协调共同规范）中提出了波激振动对船体结构疲劳寿命的影响要求，希望能够理性分析波激振动引起的船体结构疲劳累积损伤，并给出科学的分析依据。全球各主要船级社和相关研究机构均参与了相关问题的学术探讨。因此，开展考虑波激振动的波浪载荷理论预报方法和模型试验方法研究显得迫在眉睫。

波激振动模型试验是针对超大型船舶开展的一种波浪载荷试验，本文进行了大型油船和散货船的波激振动模型试验，分析了大型船舶波激振动特征及其对船体结构疲劳的影响。在此基础上，为了快速计算各种短期海况下的船体非线性波激振动，利用规则波中低频和高频弯矩传递函数特点，本文提出了一种分析短期海况中非线性波激振动现象的快速计算方法。最后基于该对实船的疲劳累积损伤进行了分析，给出了不同航线上高频波激振动对疲劳累积损伤的长期影响，为提高大型船舶的结构安全性提供参考。

1 模型试验设计

试验对象为一艘30.8万吨的油船和20.5万吨的散货船，模型缩尺比分别取为55和50，为分段龙骨梁型玻璃钢拖航弹性船模，在第2站、4站、6站、8站、10站-50mm、12站、14站、16站和18站共9个剖面上分段，共10段。根据最新的HCSR[8]文本，油船以满载和压载这两个装载状态进行疲劳强度的评估，航速取设计航速。为此，根据装载手册，结合静水弯矩、吃水这两个因素，选择满载到港和压载离港两个典型装载状态开展模型试验。

船模的设计及航行状态应满足几何相似、运动相似、动力相似原则。实船与模型主要尺度与参数，列于表1和表2中。其中实船船体梁垂向二节点振动频率f2由三维水弹性程序计算获得。油船分段模型如图1所示。

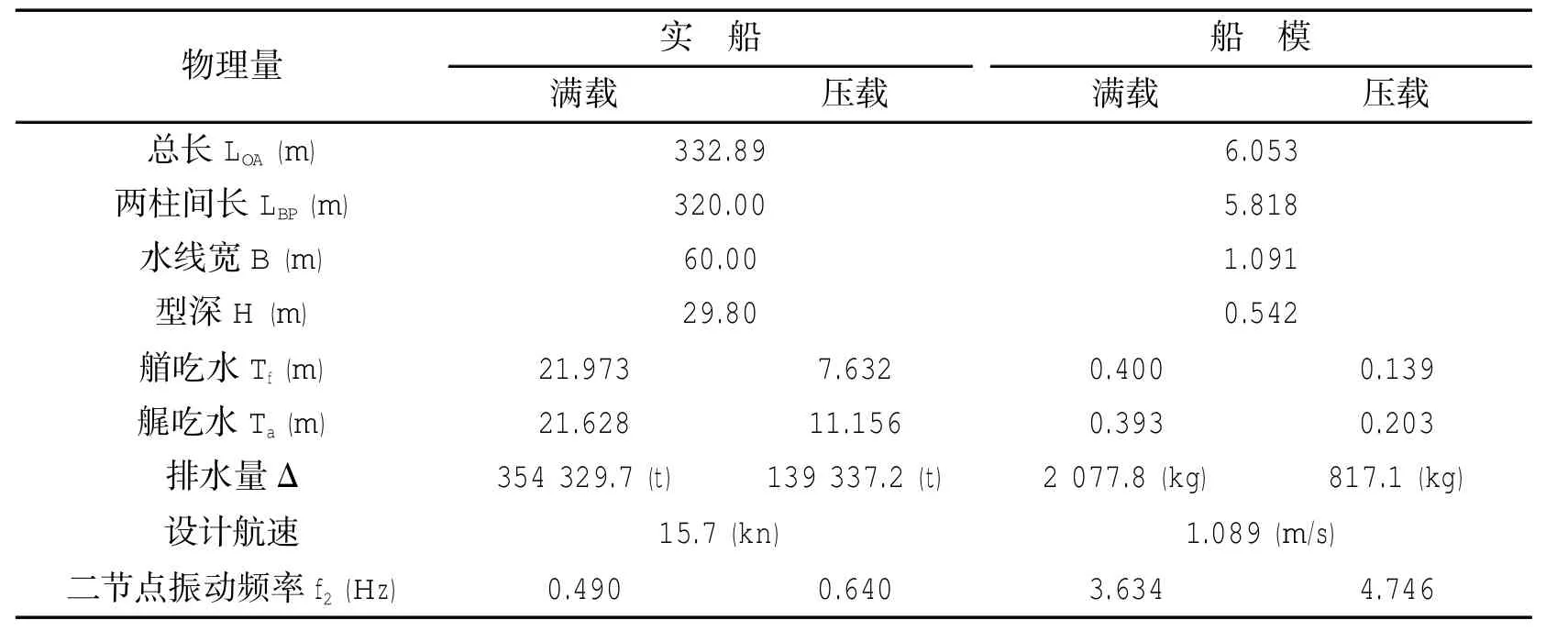
表1 油船（VLCC）主要参数Tab.1 Main parameters of the VLCC

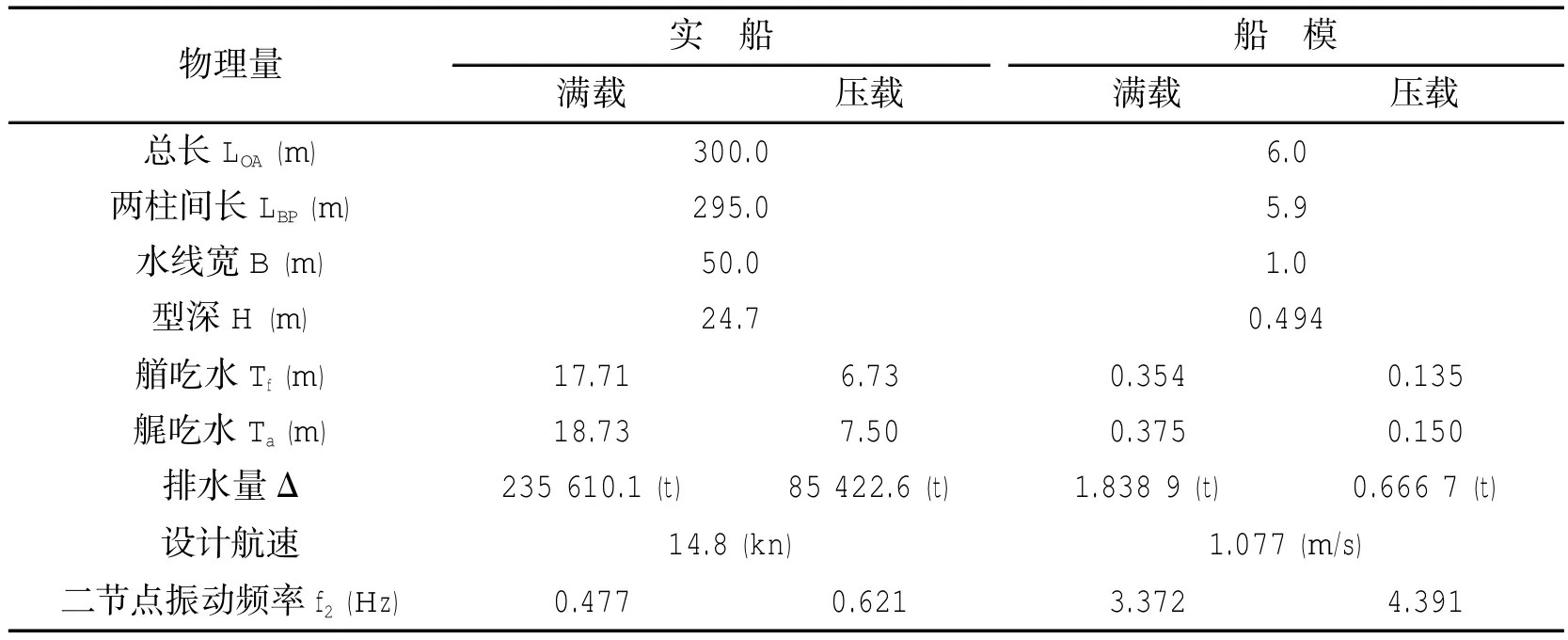
表2 散货船（BC）主要参数Tab.2 Main parameters of the Bulk Carrier

图1 VLCC龙骨梁分段弹性模型以及弯矩测点布置示意图Fig.1 Sketch map of ten segments model and points of moment measuring for VLCC

由于波激和砰击均会产生船体梁高频弯矩响应，而且波激和砰击很难区分。为了在规则波模型试验中尽量避免砰击的产生，而主要关注波激振动现象，在规则波模型试验中波高分别选为80 mm和200 mm，相当于实船4 m和10 m波高。试验表明在80 mm波高下只有波激振动现象而基本没有砰击产生，但200 mm波高时在发生波激现象的同时有明显的砰击现象。

在静水零航速时，通过捶击方式测量静水中船体二节点垂向振动频率，其结果见表3。从表中可以看出通过水弹性理论计算可以较为准确地得到船体二节点振动频率，可见水弹性理论预报湿模态船体二节点振动固有频率是十分有效的。

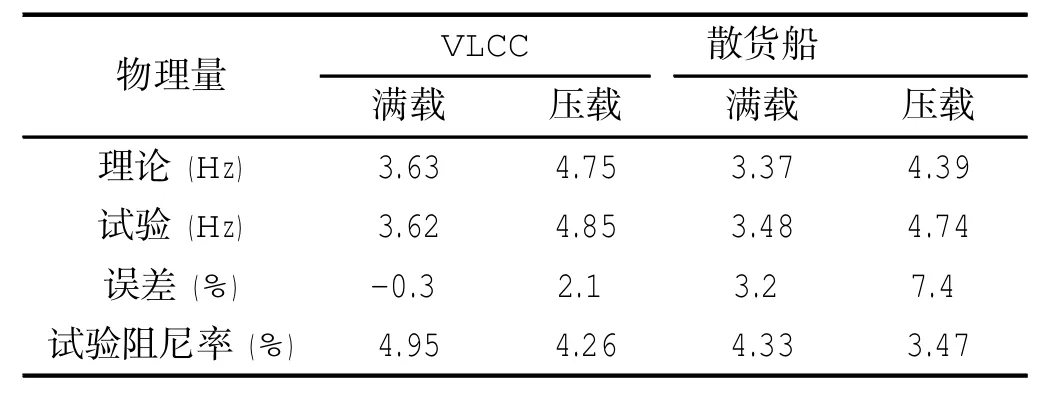
表3 模型二节点固有频率的理论值与试验值Tab.3 Theoretical and measured two-node frequency of the models

2 试验结果分析

2.1 规则波结果分析

油船压载工况下舯剖面的规则波试验典型信号记录曲线 （包括波浪信号和舯剖面弯矩信号）如图2，图中船体舯剖面弯矩响应曲线达到稳定后存在明显的高频成分。通过观察试验录像此工况并未发现有砰击现象，可以判断图2工况中发生了明显的波激振动现象。

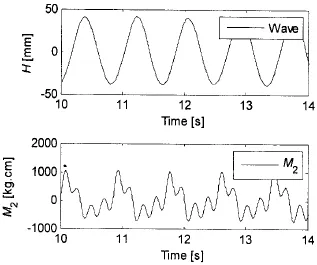
图2 典型波激振动信号记录Fig.2 Typical signal record of springing

对图2信号进行带通滤波后可以分别得到该信号的低频和高频信号，高低频时域曲线和各种频率成分能量分布曲线分别如图3和4。从波激振动时域曲线图3可以看出该工况中存在很明显的波激振动现象，高频部分振幅稳定没有衰减。图4中1.2 Hz位置的峰值为波浪遭遇频率成分，波浪遭遇频率的四倍频率与船体梁二节点频率基本重合，因而激起了明显的二节点振动。该现象说明船体湿表面变化引起的非线性波浪载荷中的某阶倍频力可能引起导致船体梁共振，从而引发非波激振动现象。

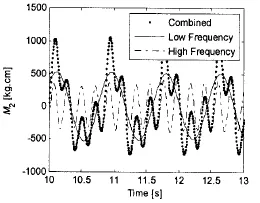
图3 波激振动信号时域曲线Fig.3 Springing signal in time domain

图4 波激振动信号频谱图Fig.4 Springing signal in frequency domain

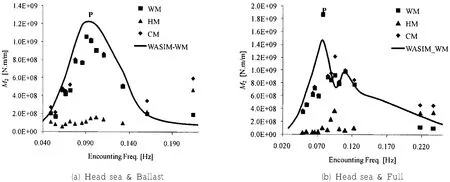
图5 油船垂向弯矩传递函数Fig.5 RAO of vertical bending moment for the oil tanker

图6 散货船垂向弯矩传递函数Fig.6 RAO of vertical bending moment for the bulk carrier

通过对各种模型试验响应结果的缩尺转换，可以得到实船在相应工况下的波浪载荷传递函数等结果。实船舯剖面弯矩的传递函数如图5和6所示，其中“WM”代表波频弯矩，“HM”代表高频弯矩，“CM”代表合成弯矩，“WASIM_WM”代表商用软件WASIM的波频弯矩计算结果。另外图5（a）和图6（a）、图5（b）和图6（b）相对应曲线（WM和WASIM_WM）的趋势较为相近，这在一定程度上说明了数值计算结果和实验结果的可靠性，但同时也说明了理论数值计算结果与试验还是存在一定差异的。从图5和6中可以发现在波浪遭遇频率超过0.2 Hz后存在很明显的倍频力激起的波激振动现象，例如图4中给出的油船压载工况下对应的实船波浪遭遇频率为0.16 Hz，此时就已引起较大的波激振动了。

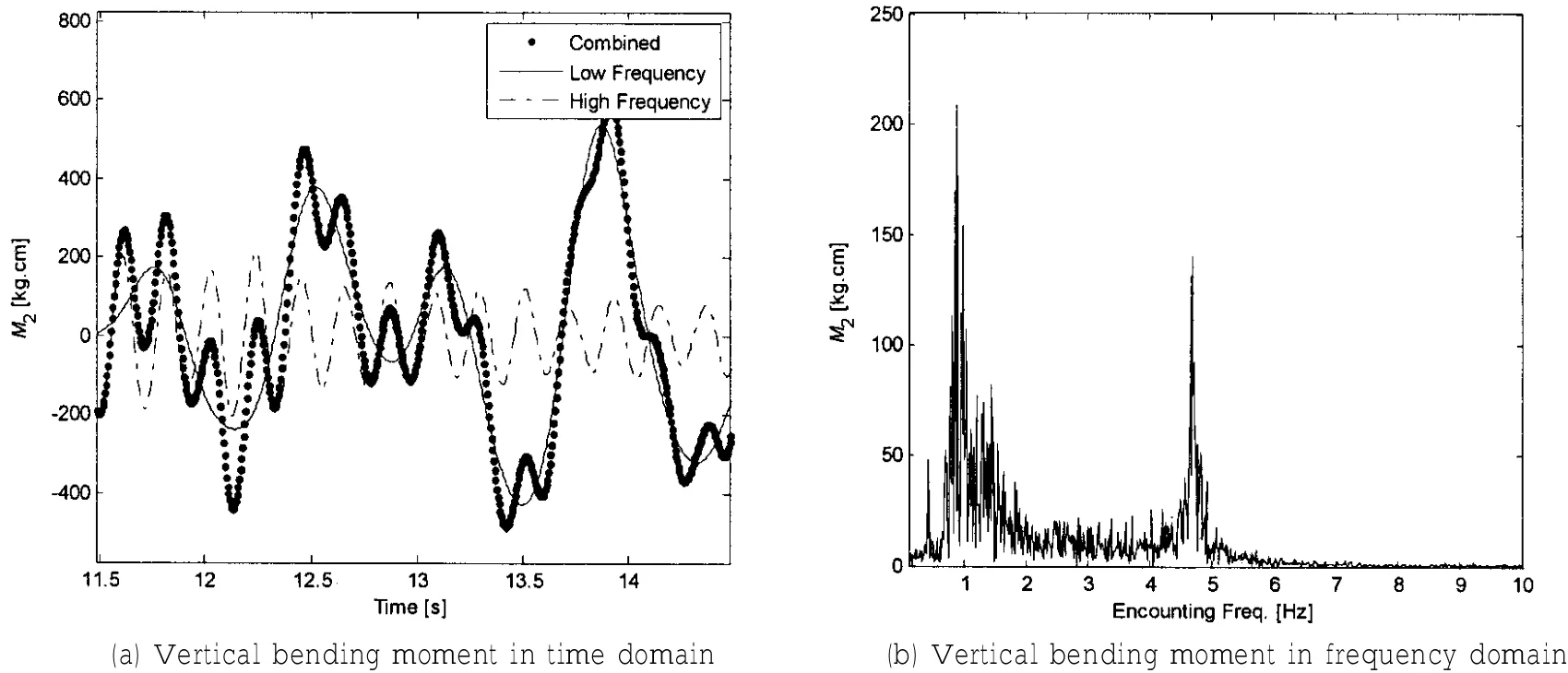
图7 油船不规则波模型试验弯矩信号（H1/3=70 mm，Tz=0.921 s，顶浪，压载）Fig.7 Responses of the oil tanker model in irregular waves(H1/3=70 mm,Tz=0.921 s,Head sea&Ballast)

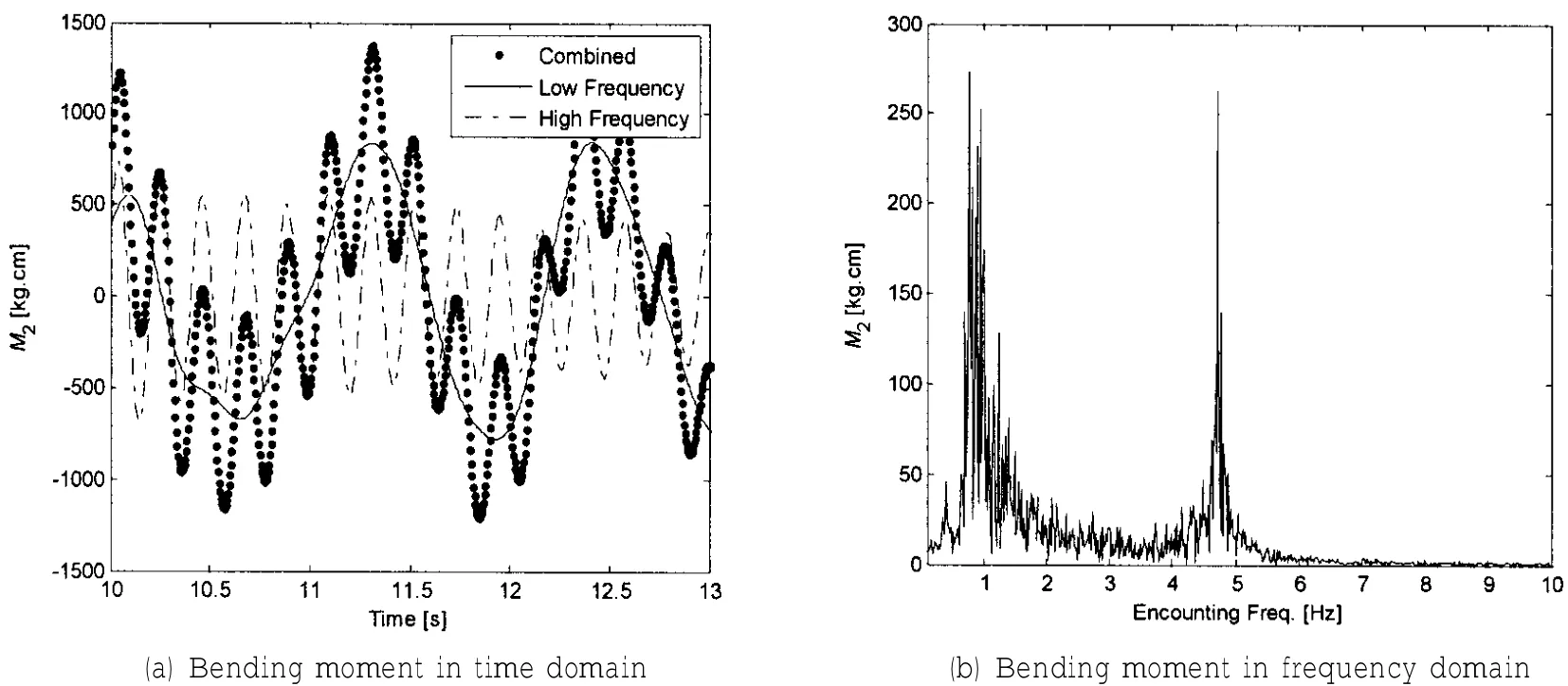
图8 油船不规则波模型试验弯矩信号（H1/3=70 mm，Tz=1.011 s，顶浪，压载）Fig.8 Responses of the oil tanker model in irregular waves(H1/3=70 mm,Tz=1.011 s,Head sea&Ballast)

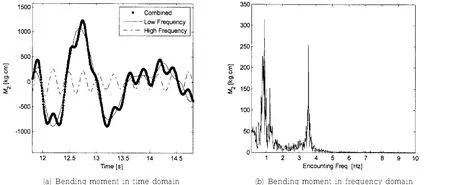
图9 油船不规则波模型试验弯矩信号（H1/3=70 mm，Tz=1.011 s，顶浪，满载）Fig.9 Responses of the oil tanker model in irregular waves(H1/3=70 mm,Tz=1.011 s,Head sea&Full)

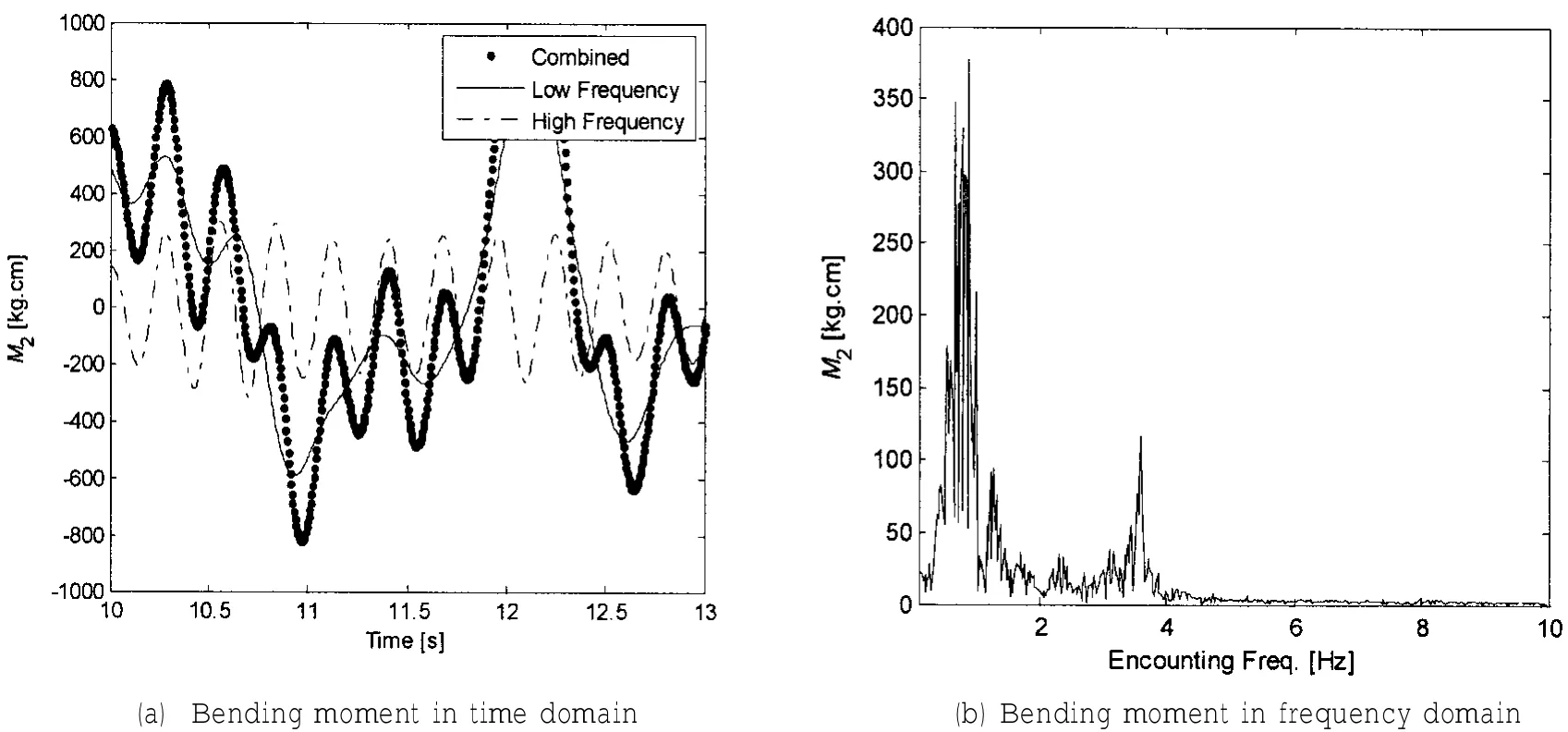
图10 油船不规则波模型试验弯矩信号（H1/3=70 mm，Tz=1.126 s，顶浪，满载）Fig.10 Responses of the oil tanker model in irregular waves(H1/3=70 mm,Tz=1.126 s,Head sea&Full)

2.2 不规则波结果分析

为了研究不规则波中的波激振动现象，本文对油船和散货船进行了压载和满载工况下六种不规则波工况（有义波高3.5 m左右）的顶浪模型试验，其中船舯剖面的垂向弯矩的时域和频域响应曲线如图7～10所示。从图中可以看出在记录得到的信号中存在很明显的高频弯矩响应成分，说明在图中所示四种工况下存在较为明显的波激振动现象。由于波浪主要能量的频率远远小于船体梁二节点振动频率，此时的波激振动应该是由高频非线性波浪力激起的（例如倍频力与和频力）。

3 波激振动对结构疲劳的影响分析

3.1 波激振动对结构疲劳影响的简化分析方法

一般情况下不规则波引起的非线性波激振动需要通过非线性水弹性程序进行计算，无论是频域的还是时域的非线性水弹性力学程序，针对每个短期海况进行一次计算总是较为耗时的。为了较快地分析不规则波引起的非线性波激振动及其对结构疲劳的影响，本文接下来将给出一种基于规则波传递函数来计算不规则波中非线性波激振动的快速方法。

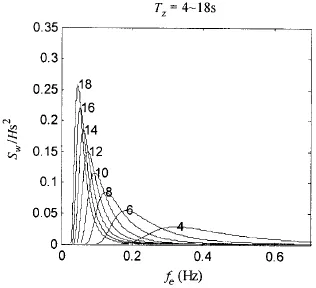
图11 ISSC双参数海浪谱Fig.11 ISSC two-parameter wave spectra

3.1.1 船体波激振动产生原因

相对于波浪遭遇频率，船体梁的自振频率较高，即使对于频率较低的超大型船舶，比如此次计算超大型油船，其压载状态下的二节点自振频率也达到了0.64 Hz。海上波浪的平均跨零周期为3～18 s，当船舶的顶浪航速为15.7 kns时，不同跨零周期下的ISSC双参数谱形式如图11所示，其中横坐标fe代表波浪遭遇频率，纵坐标代表波浪能量。从图中可以看出绝大部分波浪能量的频率远小于船体梁二节点振动频率，说明波频成分很难激起船体梁波激振动。但是由船体非线性波浪力引起的倍频成分可以激起较为明显的波激振动，例如二分之一和三分之一的船体梁二节点振动频率为0.32 Hz和0.21 Hz，在这样的波浪遭遇频率附近波浪能量还是较大的，特别是对于波浪平均周期较小的不规则波。这样的不规则波将会引发比较明显的船体梁波激振动现象。

3.1.2 船体波激振动响应快速计算方法

（1）规则入射波

既然船体梁的波激振动主要是由高阶的倍频力激起，那么相当于一个低频的规则入射波浪，可以激起至少两个不同频率的规则波响应，其中一个频率是和遭遇频率ωe对应低频响应，一个频率是船体二节点自振频率ω1处的高频响应（从规则波和不规则频谱图中均可以看出），还有一些能量较小的不同倍频下的响应成分。简化起见，将规则来波下的船体结构合成弯矩响应表达为上述两个主要频率成分的叠加形式：

其中：ML和MH分别为低频和高频弯矩响应幅值；ωe和ω1分别为波浪遭遇频率和船体梁二节点振动频率；εL和εH分别为低频和高频响应的初始相位。通过这种方法，可以近似得到任一规则波激励下的船体梁低频和高频合成响应，从而可以分别得到低频和高频波浪载荷传递函数，例如图5和图6。

（2）不规则入射波

通过等频率间距或者等能量法可以模拟海浪能量谱的时域现实，其表达式为：

其中：ξi为规则波幅值；ωi为规则波圆频率；εi为规则波初始相位。

不规则入射波情况下不仅有倍频高阶力，还有其它和频高阶力。当不考虑其它和频高阶波浪力，仅考虑倍频高阶力时就可以使用我们在规则入射波中的方法表达船体梁的响应。此时不规则入射波中的时域合成弯矩响应表达式为：

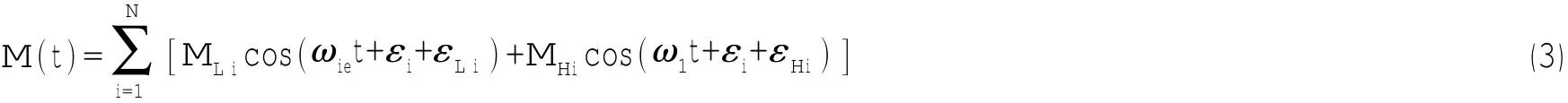
其中：MLi和MHi分别为低频和高频弯矩响应幅值；ωie和ω1分别为波浪遭遇频率和二节点振动频率；εLi和εHi分别为低频和高频响应相对于波浪的相位。另外，

其中：ALi和AHi分别为低频和高频传递函数，可以通过模型试验获得。

然后使用船体梁弯矩响应除以剖面模数得到不同结构的应力时域响应曲线，再通过雨流计数法统计疲劳载荷参数。

3.2 短期海况中波激振动对疲劳损伤的影响

通过上面提出的快速计算方法我们可以得到短期海况下船体垂向弯矩响应的时域曲线和频谱图，如图12和13所示，图中同时列出了通过相应工况下的试验测量结果。从图12和13可以看出计算得到的结果与试验测得的数据较为一致，说明了本文提出的方法在快速计算波激振动响应时的合理性。

为了计算短期海况中波激振动对船体结构疲劳的影响，同时为了进一步验证上节的快速计算方法的有效性，本文针对试验中测得的短期海况下的弯矩测量结果计算了主甲板典型构件1小时疲劳累计损伤。在船体结构疲劳累积损伤评估中一般采用如下的S-N形式：

式中：m、m′和A为结构疲劳参数；S和N分别为应力范围水平和应力循环次数，SQ和NQ为图14中交汇点Q的应力范围和应力循环次数；一般NQ=107，m=3.0，m′=5.0。另外

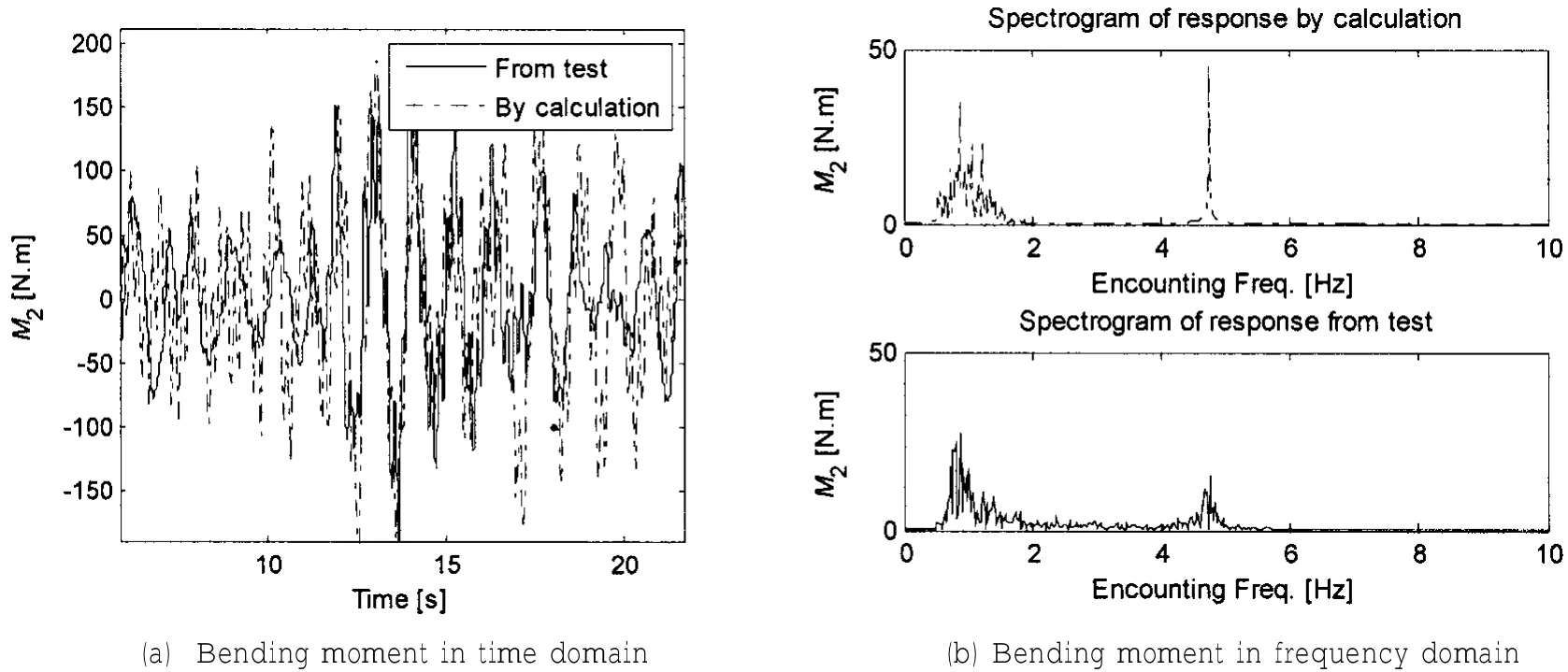
图12 油船不规则波模型试验弯矩比较（H1/3=70 mm，Tz=1.011 s，顶浪，压载）Fig.12 Comparison of bending moment in irregular wave model tests of oil tanker (H1/3=70 mm,Tz=1.011 s,Head sea&Ballast)

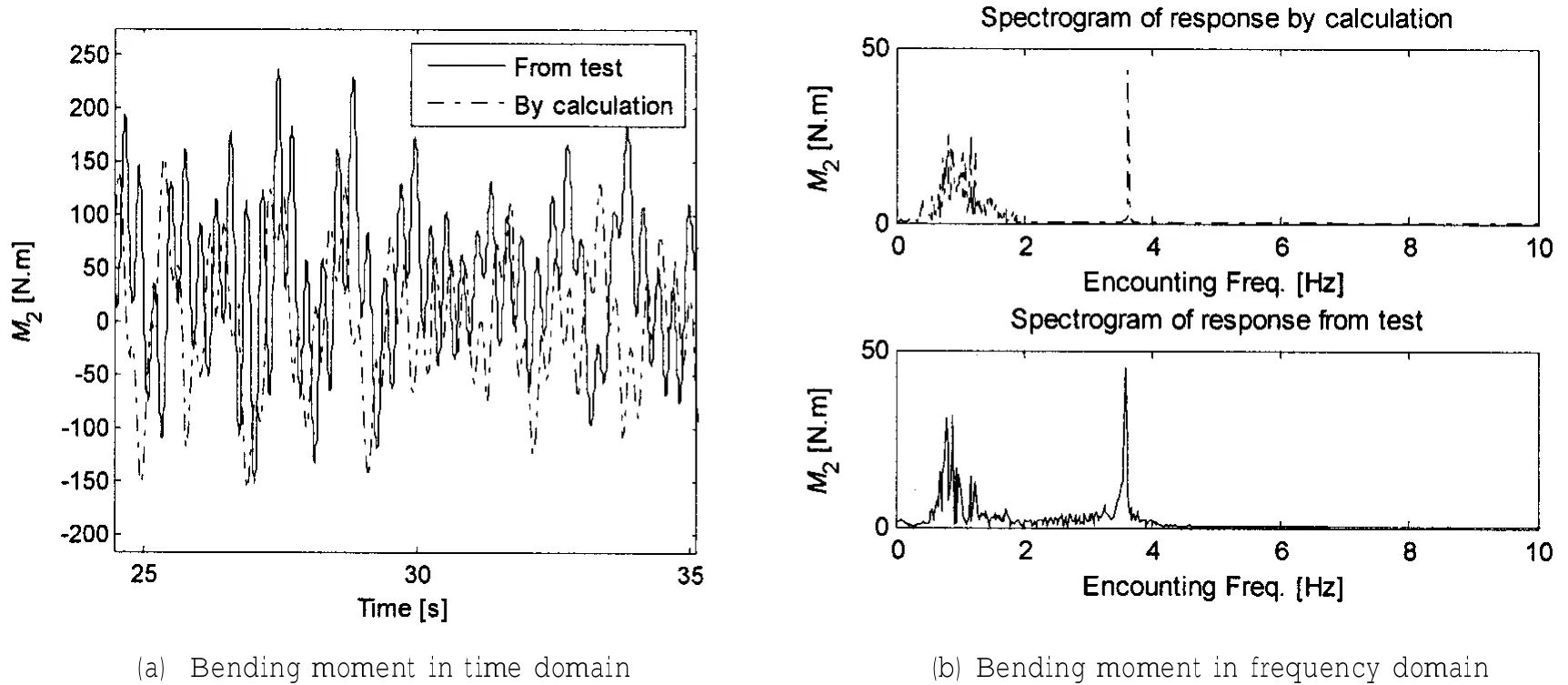
图13 油船不规则波模型试验弯矩信号（H1/3=70 mm，Tz=1.011 s，顶浪，满载）Fig.13 Comparison of bending moment in irregular wave model tests of oil tanker (H1/3=70 mm,Tz=1.011 s,Head sea&Full)

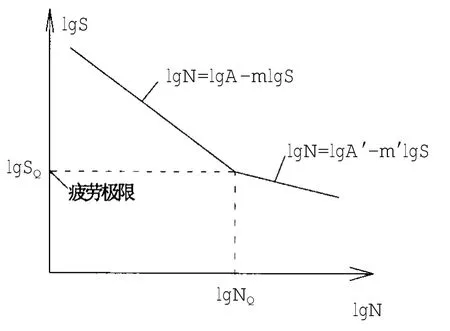
图14 S-N曲线Fig.14 S-N curve

本文油船的甲板剖面模数和应力集中系数分别取为56.4 m3和1.12，散货船的甲板剖面模数和应力集中系数分别取为55.4 m3和2.0，S-N曲线选自HCSR[8]的D曲线，计算结果如表4和表5所示。从这两个表中可以发现跨零周期Tz越小，合成弯矩引起的疲劳累积损伤与低频波浪弯矩引起的损伤之比越大，说明此时的波激振动对结构疲劳影响越大。同时两表中用上节的快速计算方法计算出的结果与试验结果最大相差-25%，最小相差2.7%。虽然疲劳结果最大相差-25%，然而由于疲劳结果是应力的3～5次方，因此计算得到的应力与试验测量结果其实仅相差5%～8%，这说明本文给出的方法还是具有较高精度的。

表4 油船合成与低频疲劳累积损伤比值（顶浪，压载）Tab.4 Ratio of fatigue damage induced by combined and low frequency for oil carrier(head sea&ballast)

表5 油船合成与低频疲劳累积损伤比值（顶浪，满载）Tab.5 Ratio of fatigue damage induced by combined and low frequency for oil carrier(head sea&full)

3.3 长期海况中波激振动对疲劳损伤的影响

由于试验成本和时间的缘故，试验中能够测量的短期海况结果终归是较少的，为了研究长期海况中的波激振动对疲劳的影响可以使用上节提出的方法进行快速而有效的计算。为了较为典型地说明问题，本文挑选了六条航线：北大西洋、澳洲、南美、中东、西非和全球。由于顶浪情况下的波激振动现象更为明显，本文将只计算顶浪工况下的长期疲劳累计损伤来说明问题。油船和散货船的设计年限按照HCSR[8]定为25年，出航系数定为0.85，其他参数与上节相同。从表中可以看出压载工况下波激振动对疲劳的影响很明显，尤其表6中合成/低频结果在2.18～3.59之间，表7中合成/低频结果在1.30～ 1.88之间，表7中的波激振动现象较表6明显是因为表中散货船的应力较大，疲劳参数m主要取3.0，而油船的应力较小，疲劳参数m主要取5.0。对于油船当m=5.0时，合成/低频疲劳损伤结果从2.18～ 3.59，那么合成/低频弯矩结果为1.17～1.29；对于散货船当m=3.0时，合成/低频疲劳损伤结果从1.30～ 1.88，那么合成/低频弯矩结果为1.09～1.23。

因此如果考虑波激振动对疲劳寿命的影响，压载顶浪工况下油船和散货船的总纵弯矩水平应该提高9%～29%。另外表6和7中合成/低频结果在2.18～3.59和1.30～1.88之间，也即低频/合成结果分别为28%～46%和53%～77%，说明此时低频弯矩对总疲劳累积损伤的比率可能比较小（最小28%），高频的影响十分重要。从表6和7中还可以发现不同航线下波激振动对疲劳损伤的影响差别较大。

表6 油船疲劳累积损伤结果Tab.6 Cumulated fatigue damage results of oil tanker

表7 散货船疲劳累积损伤结果Tab.7 Cumulated fatigue damage results of bulk carrier

续表7

4 结 论

通过开展大型油船和散货船的波激振动模型试验和计算波激振动对船体疲劳寿命的影响，同时结合本文提出的简化方法计算短期和长期海况的疲劳寿命，得出了以下结论：

（1）规则波试验中发现波浪频率从1/4二节点振动频率开始就有较为明显的波激振动现象；

（2）不规则波试验中发现波激振动的高频信号主要集中在二节点频率附近；

（3）300 m级油船和散货船的波激振动主要是由非线性高频弯矩引起的，而非波频弯矩；

（4）如果考虑波激振动对疲劳寿命的影响，压载顶浪工况下油船和散货船的总纵弯矩水平应该提高9%～29%；

（5）压载顶浪工况下低频弯矩对总疲劳累积损伤的贡献占28%～77%。

（6）不同航线下波激振动对疲劳损伤的影响差别较大。

[1]Storhaug G.Experimental investigation of wave induced vibration and their effect on the fatigue loading of ships[D].Ph.D thesis,Norwegian University of Science and Technology,2007.

[2]Wu M K,Moan T.Sensitivity of extreme hydroelastic load effects to changes in ship hull stiffness and structural damping [J].Ocean Engineering,2007,32:1745-1756.

[3]Iijima K,Yao T,Moan T.Structural responses of a ship in severe seas considering global hydroelastic vibrations[J].Marine Structures,2008,21:420-445.

[4]Pedersen P T,Jensen J J.Estimation of hull girder vertical bending moments including nonlinear and flexibility effects using closed form expressions[J].Proceeding of IMechE,Part M:J Engineering for the Maritime Environment,2009,223(3): 377-390.

[5]汪雪良,顾学康,胡嘉骏.基于模型试验与三维水弹性理论的船舶波激振动响应研究[J].船舶力学,2012,16(8):915-925. Wang X L,Gu X K,Hu J J.Springing investigation of a ship based on model tests and 3D hydroelastic theory[J].Journal of Ship Mechanics,2012,16(8):915-925.

[6]Storhaug G,Vidic-Perunovic J,Rudinger F,Hoitsmark G,et al.Springing/whipping response of a large ocean-going vessel-A comparison between numerical simulations and full scale measurements[C]//Proceeding of the 3rd International Conference on Hydroelasticity in Marine Technology.Oxford,UK,2003:117-131.

[7]Drummen I,Storhaug G,Moan T.Experimental and numerical investigation of fatigue damage due to wave-induced vibration in a containership in head seas[J].J Mar Sci Technol,2008,13:428-445.

[8]IACS.Common Structural rules for bulk carriers and oil tankers(HCSR)[S].2013,4.

[9]DNV-RP-C205.Environmental conditions and environmental loads[S].2007.

Study on springing of large oil tanker and bulk carrier and the influence to fatigue

YANG Peng1,2,GU Xue-kang2,DING Jun2,ZHANG Fan2,HU Jia-jun2
(1.Wuhan Second Ship Design and Research Institute,Wuhan 430205,China; 2.China Ship Scientific Research Center,Wuxi 214082,China)

Based on the springing model tests of one large oil tanker and bulk carrier,the phenomenon of springing is investigated;the influence of springing to structural fatigue is calculated by stress data for short-term sea state measured from model tests.Moreover,one simplified method is proposed to analyze the springing in short-term sea state and the influence to structural fatigue.And,the influences of springing to structural fatigue in long-term sea state for some typical sea routes are studied.The results show that the oil tanker and bulk carrier have obvious springing under ballast condition,which is different for various routes.The simplified method could assess the fatigue damage due to springing properly,and which has some practical value in engineering.

oil tanker;bulk carrier;springing;model trial;fatigue damage

U661.71

：A

10.3969/j.issn.1007-7294.2016.10.012

1007-7294（2016）10-1320-10

2016-06-15

国家973基础研究课题（2013CB036100）

杨 鹏（1988-），男，武汉第二船舶设计研究所，博士，工程师，E-mail:yangpeng@cssrc.com.cn；顾学康（1963-），男，研究员。