喷管中气液两相混合物流动的等熵分析

郑 俊，王宝寿，陈玮琪，王军锋，李锋

（1.江苏大学能源与动力工程学院，江苏镇江212013；2.中国船舶科学研究中心，江苏无锡214082）

喷管中气液两相混合物流动的等熵分析

郑 俊1，2，王宝寿2，陈玮琪2，王军锋1，李锋1

（1.江苏大学能源与动力工程学院，江苏镇江212013；2.中国船舶科学研究中心，江苏无锡214082）

文章基于均质混合物的等熵和正压条件，建立了喷管内定常气液两相流动的等熵模型及其微分方程，并因此得到了喷管内混合物压力、体积分数、马赫数以及温度之间的等温与等熵的解析关系。解析解表明，气液质量流率之比增加，喷管内混合物的温度变化明显，而混合物的临界流动特性与滞止点的气体体积分数有关。基于以上解析关系以及连续性方程得到喷管线型与压力分布的解析关系，通过该关系可以根据期望压力分布逆向设计得到喷管线型，或者根据给定喷管线型求解得到喷管内的流动。

气液混合物；等熵流动；解析模型；极限流动；喷管设计

0 引 言

气液两相流动的应用是广泛的[1-3]，比如在推进系统的研制当中，就有所谓通气喷水推进[3-4]。水冲压气液两相推进[5-7]，金属水反应两相流推进[8-9]，喷雾推进[10-11]等多种推进方式中都涉及气液两相流。两相流推进是水下高速推进方式的研究方向，具有水下推进传统方式不具有的优点。

在气液两相流理论和数值分析方面，喷管中泡状流的研究得到了较广泛的研究。其中Tangren[12]基于等熵条件和正压模型，简单推导了喷管中的气液两相流动的特性，但其得到的结果还不足够简洁。而其它的理论分析，还主要集中在等温模型。Mor[13]基于等温条件和正压模型，简单推导了管道中的泡状流动模型，但并未给出流动参数满足的解析关系。基于等温模型，Wijngaarden[14]研究过幅度较小和中等的压力波在泡状流中的传播问题，并分析了气泡大小、波长、波幅、以及气泡间距对压力波的影响，并指出一维条件下波的传播方程类似于Korteweg-de Vries方程。Eddington[15-16]较早地研究了气液两相的超音速流动问题，并且导出了无相对滑移的气液两相流的激波条件。Thang[17]则给出了气液两相具有定常相对滑移速度下的激波条件。针对水冲压发动机，国内的付英杰[6]和董磊[7]也进行了一定的探索。其中付英杰基于Rayleigh气泡动力学方程求解了喷管中泡状流动等；而董磊基于CFD软件Fluent中的不可压缩均质混合物模型探讨了外悬式水冲压发动机的推进性能，但两者对于喷管中可压缩泡状流的解析模型或可压缩泡状流的CFD仿真，还未有针对性地开展过。

本文基于气液两相混合物的等熵条件以及正压模型，对喷管中气液两相流动的基本原理进行分析，并且得到了一系列具有显著物理含义的简化关系式，得到了流动的基本微分方程及其相应的解析解，最终用于喷管中的流动计算和喷管线型的逆向设计。

1 气液两相等熵流动的基本方程

对于喷管中的气液两相准一维等熵流动分析，基于以下的理论前提：（1）气液两相总体是等熵的，但是允许气液两相之间存在热传递；（2）气液两相没有相变；（3）气液两相共有压力且无相对速度。需要指出的是，在气体体积分数过大的情况下，相对速度的影响将表现出来；关于相对滑移速度的影响，将在未来的工作中进行。

1.1 气液两相等熵流动的基本方程

质量守恒方程

能量方程（等熵条件）

混合物组成

气体状态方程

马赫数定义

等熵声速定义

其中：物理量U为流速，P为压力，A为喷管截面积，F为喷管轴向单位长度上的摩擦力，为混合物质量流率，α为气体体积分数，R为气体常数，T为热力学温度，c为声速，s为混合物熵。其中下标a，l分别指气体与液体。

根据（1）、（4）式和（5）式可知，如果压力和温度以及质量流率可知，那么ρ，ρa，α可求，即它们之间并不独立。因此如果流量给定,那么ρ，ρa，α都只是压力P和温度T的函数。而（3）式将给出压力和温度的关系，从而最终理论上可以求得混合物密度ρ和压力P、温度T的关系。

1.2 混合物状态方程

将（4）式代入（1）式可以获知

并因而可以得到：

引入气液质量流量之比为常数

并因而可以得到：

由（12）式可以得到

由（13）式可以得到

将（15）式代入（5）式，并将（14）式随后代入，就可得到

或

其中

上述（16）式就是泡状流正压模型的状态方程，需要注意P，Pt都是温度T的函数。

1.3 气液两相混合物的等熵关系

等熵声速需要从等熵关系导出。因此首先来研究混合物的等熵关系。将（3）式展开并写成

即表明，气液两相混合物的总熵为0。由（19）式和（11）式可以得到

由熵增的定义可知

其中：dWa表示因为气体微元体积变化时压力对外做功；而水的熵增为

水体积不变，其压力并不对外做功。将（21a）和（21b）代入到（20）式，可得：

如果气液两相为热平衡，那么两相的温度相等

将上式代入（22）式有

又因为

将（5）式代入上式有

将（26）式代入（24）式可以得到

因为有

其中

其中

为水和气体的定容比热的比值，因为水的比热容比气体大很多，所以κ大于1。ω可以认为是当前喷管内的气液混合后的某个常数，它可以表示不同气液质量流率和不同比热容气体和液体定常混合后的性质。那么由（29）式就可方便地得到

这个式子的形式非常典型。当气体的质量流率远远大于水的质量流率时，那么有

（32）式的形式就退化为纯气体的等熵关系；在一般的泡状流动中，μ的量级很小，η是个接近0的量，这就导致ω接近0，从而使得（32）式右端的值接近1，从而流动中温度几乎没有变化。可以将（32）式的等熵关系转化为压力和密度的关系。将（5）式代入（32）式，并继而再将（15）式代入后有

（32）式和（34）式就是气液混合物的等熵关系。

1.4 气液两相混合物的声速方程

现在需要根据压力和密度的等熵关系（34）式来求解声速方程。对（34）式两边密度求导有

又因为将（16a），（16b）式两边各自相乘，并化简就可以得到

定义无量纲的压力特性函数

（35）式就可以简化为

将（16a）式变形并写为

定义虚拟声速

可以得到

为方便，记

将（42）式代入（41）式可以得到

事实上由（14）式和（36）式，可以得知

那么声速（43）式又可以表达为

注意，ct现在是温度的函数。从（45）式可以看到，管道内给定气液混合比的气液两相流声速是与体积分数成反比的。由（6）式和（43）式可以得到

2 基本微分关系

为了得到流动的微分方程，需要得到各变量的微分关系。因此要建立温度、密度、压力和速度之间的微分关系。由（18）式可知

由（16a）式两边取微分并利用（37）式可以得到

同理由（40）式可以得到

同理又由（37）式可以得到

为了进一步运算的简便，考虑将所有的量转换成无量纲压力特性函数P¯的微分关系。于是将（47）式以及（29）式代入上式并化简就有

于是将（51）式代入到（47）式和（29）式，可以得到

将（50）式代入（48）式可以得到

由（49）式和（52）式可知

由（44）式可以容易得到

可以很方便地由（1）式得到

也可以很方便地由（46）式得知

将（54）式代入（57）式可以得到

将（53），（58）式代入（56）式，可以得到

3 气液两相混合物等熵流动微分方程

将（8）～（11）式以及（46）式以及（51），（58）式代入动量方程（2），并忽略摩擦力，有

将（60）式代入到（59）式，可以得到

将（44）式和（55）式代入（60）式就可以得到

以上方程组（60）～（62）就是气液两相等熵流动的基本微分方程组。注意，当ω=0时，由（29）式可知，方程组的形式就完全退化为等温流动的情形。方程组（60）～（62）对于泡状流和雾状流都是近似合适的。现在让我们来进一步分析方程组解的情况。将（62）式写为

或

则，（63a）式进一步转换为

在等温情形下，即ω=0时，（65）式或（63a）式可以给出很简洁的结果：

等熵情况下，方程（65）给出的结果是

其中

为方便起见我们称之为气液混合指数。将边界条件

也代入到（67）式，定出常数C，可以得到

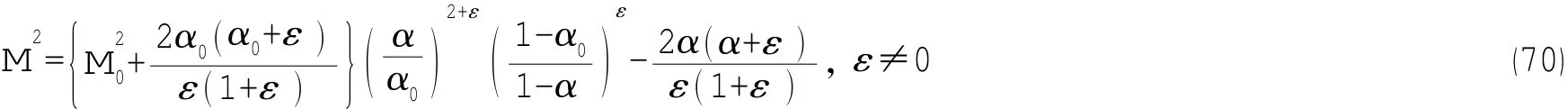
这就是气液两相流动等熵情形下的解析解；注意到（70）式不适用于ε=0或ω=0的情况，也就是不适用于等温情形。等温情形下，请采用（66）式进行分析。注意到，当（69）式中M0≈0时，该条件则为滞止条件；而一般情况下，（69）式也可以作为入口条件。

4 气液两相混合物等熵流动特性分析

为方便继续分析，让我们来考察气液不同混合条件下，混合指数ε的取值情况。可以从（30），（68）式发现对于特定的气体和液体（从而它们的定容比热不变，以及气体的绝热指数γ固定），ε仅是随气液质量流率比值μ变化的单增函数，如图1所示。

图1 气液混合物指数εFig.1 The mixture exponent ε

当气体的质量流率远远大于水的质量流率时，即μ趋近于无穷大时，ε趋近于固定值，如图1中的横虚线所示，这个值仅由气体的绝热指数决定。当气液质量流率相等，即μ为1时，ε取值为10-1；对于泡状流动而言，μ接近的量级在10-4～10-2之间时，ε取值仅在10-5～10-3之间。所以对于泡状流动而言，ε是一个绝小的量。由于气体密度远远小于水，当气体与液体的质量流率相当甚至小一个量级时，即μ的量级接近10-1～100之间时，气体体积分数会相当大，流态可能接近雾状，此时ε取值仅在10-3～10-1之间。雾状流动的气液相对滑移速度比较大，因此本文基于无相对滑移的考察，对于雾状流动，可能误差会相对显著一些。下文中，我们在定性分析中只给定气液混合物的混合指数ε，并且始终注意到它对应于某一特定的气体和液体的质量流率比值μ，ε较大时，对应于μ也取较大的值。

4.1 气液两相混合物等熵流动温度变化

有必要来考察一下，气液两相流在喷管中流动时，其温度的变化。由（32）式和（37）式以及由（18）式和（68）式可以得知

利用（44）式可以得到

基于（72）式可以看到对于不同的气液混合指数ε，在给定不同入口体积分数α0下，流动的温度随气体体积分数α的变化，如图2所示。由图中可以看到，给定入口体积分数α0，随气体体积分数α的增加，温度不断降低。也就是说随着气体在流动中的膨胀，混合物的温度不断降低，而随着气体被压缩，混合物温度则不断增加。而且可以看到，在同样的气液混合指数ε下（也即同样的气液质量流率和气液的性质），入口体积分数α0越大，则流动中的温度与入口温度的比值就越大，即温度变化越不显著；这说明入口体积分数α0越小，则膨胀到同样的α时，温降就越大。从图2还可看到，对于同样的入口体积分数α0下，气液混合指数ε对于温度变化过程也有影响；可以发现，当流动中的气体体积分数α小于0.5时，ε大的气液混合物的温度比值要高于ε小的气液混合情形，而当气体体积分数α大于0.5时，ε大的气液混合情形下的的温度比值要小于ε小的气液混合情形。这说明当气液混合指数ε大时，流动中的温度变化较为明显，气体在其中的影响更大；这说明为了更好地利用气液混合物的内能，一定程度上增加ε的值是有益处的。

图2 温度随气体体积分数的变化Fig.2 The temperature variation vs.the air volume fraction

图3 马赫数随气体体积分数的变化Fig.3 The Mach number variation vs.the volume fraction of air

4.2 气液两相混合物等熵流动的基本特性

以上得到了流动中温度随气体体积分数的变化关系，有必要继续分析流速或流动的马赫数的变化特性，根据（66）或（70）式可以分析马赫数与气体体积分数变化特性，如图3所示。从图3中可以发现，在不同的滞止点体积分数α0下，随着气体体积分数α的增加或气体的膨胀，流动的马赫数是不断增加的。可以发现，流动膨胀到同样的气体体积分数α，滞止体积分数α0越小，流动达到的马赫数越大，也即流动越快。还可发现，当气液混合指数ε越大，那么在同样的滞止体积分数α0下，流动达到同样的气体体积分数α时，流动的马赫数也越大；当α0越大时，气液混合指数ε的影响就越小。结合图2可知，气液混合指数ε对流动的影响，是来源于不同气液混合情形下，温度变化的不同。α0越大时，混合物膨胀的余量将越小，因此温度变化也会越小，流动基本是等温状态，因此气液混合指数ε不同值的影响就越小。需要指出的是，当ε极其小时，等熵流动和等温流动是基本重合的，所以ε较大时与ε较小时流动的差别，基本上反映了等熵流动与等温流动的差别。

4.3 气液两相混合物等熵流动的极限流动

如果气体以小气泡的形式分布在液体中，并且气泡与气泡之间是独立的，那么这种流动就可看做是泡状流。在这种流动中，气泡具有几何极限，即保证气泡分散时气泡最大的半径下的体积分数。近似计算下，该极限下的气泡体积分数约为0.74[13]。因此当气体膨胀到最大体积分数α为0.74时，那么根据（70）式就可得到不同滞止体积分数α0下，对应于α为0.74时的马赫数，如图4所示。从图中可看到，不同的滞止体积分数α0下，当流动达到的极限体积分数α=αlim=0.74时，极限马赫数是不同的；比如当滞止体积分数α0为0.3时，流动能达到的极限马赫数约为2。滞止体积分数α0越小，则流动能达到的极限马赫数也越大，也即气体膨胀的效率越高。

图4 对应于不同气体极限体积分数，不同滞止条件α0下能达到的极限马赫数Fig.4 Limited Mach number could be reached for different limited volume fraction αlim

若极限体积分数并不局限于泡状流的0.74，而是可继续膨胀以致流动成为雾状流，从而气体的极限体积分数可达到更高，那么在同样滞止体积分数α0下，流动能够达到的极限马赫数更高。比如当α= αlim=0.999时，那么当滞止体积分数α0为0.9而气液混合指数ε为0.05时，则流动能达到的极限马赫数为3.25左右。可见在同样的滞止点体积分数α0下，雾状流动所能达到的极限马赫数比泡状流动要高。从图4中还可以看到，气液混合指数ε越大，则同样的滞止点条件下，流动所能达到的极限马赫数也越大，这说明气体的质量流率增加的情况下，温度对流动影响增加，极限体积分数αlim越大，ε的影响也越大。

4.4 气液两相混合物等熵流动的临界流动

现在来考察，气液两相等熵流达到临界时，即（70）式中

时，对应于不同的滞止体积分数α0，流动达到的临界特性。为便于分析，引入临界压力特性比

其中上标“*”表示临界流动处的物理量。由（44）式可知，（74）式成为

由此可以得到

将（75）式代入（70）式，可得临界压力特性之比t与滞止点体积分数α0的关系，如图5所示。从图5可以看到滞止点体积分数α0越高，则临界流动处与滞止点处压力特性之比越接近1，也就是临界流动处的压力和滞止点处的压力越接近，喷管内的压力梯度较小；相反，滞止点处体积分数α0越小，临界流动处和滞止点处压力特性相比就越小，喷管内的压力梯度就越大，压力增效就越大。因此在相关的发动机设计中，必须要求在保证气体流率的条件下，入口处的气体体积分数越小越好，也就是入口压力越高越好，气体被压缩的程度越大越好。从图5可以看到，气液混合指数ε值不同时，临界流动压力之比的特性基本是接近的；也就是说，因为不同气液流量之比μ而导致的不同的ε下，临界流动处的压力特性基本接近；即，不同气液流量之比μ的混合物在达到临界时，临界流动之前的压力增效程度是接近的。对比图5和图4可以看到，气液混合指数ε对混合物的极限流动影响颇大，而对临界流动的影响则不显著。

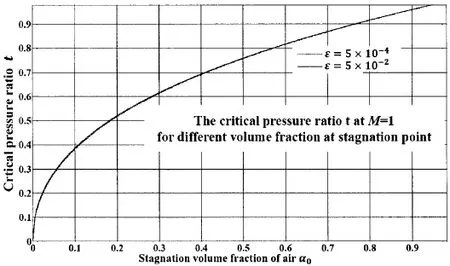
图5 临界流动处与滞止点处压力特性之比和滞止点体积分数的关系Fig.5 The ratio between the pressures at the critical and stagnation points vs.the volume fraction at the stagnation point

5 喷管内气液两相等熵模型的应用

以上基本上分析了气液两相混合物在喷管内的等熵流动的基本特性。现在尝试将两相混合物等熵流动基本关系（70）等式用于喷管设计以及喷管内相关流动的计算。

5.1 喷管线型的设计方法

由于喷管内质量守恒，根据（8）～（11）式及（46）式得到

可以立即反算出

又因为（44）式，由（70）式可以得到

由（40）、（18）式以及（71）式可知

将（78）式以及（79）式代入（77）式，就可以得到

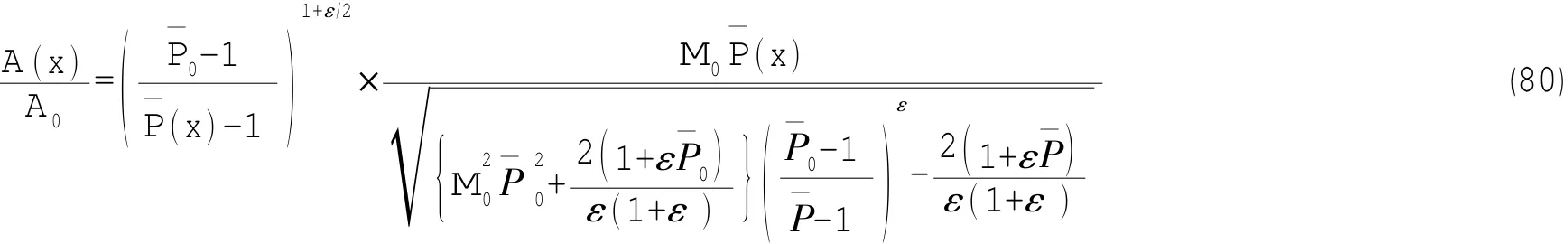
根据（80）式可知，当给定气液混合指数ε以及压力特性函数P¯（x）的分布，就能够根据方程的右边算出方程的左边，即喷管线型的无量纲分布。当给定以下的压力分布时

可得到喷管的线型如图6所示。从图6可以看到，所设计喷管为收缩扩张喷管，喷管的喉部在马赫数为1处。根据图6可知，当气液混合指数ε较大，或者气液质量流率之比μ较大时，喷管的截面积也要相应地增大。根据（80）式以及（40）式，很明显，还可以基于流速分布来进行喷管线型的设计，这里不再赘述。

图6 基于期望的压力特性分布P（ x）逆向设计得到的喷管线型Fig.6 The nozzle shape derived based on an expected pressure distribution P（ x）

5.2 喷管内气液两相混合物流动的计算

相应地，如果我们给定（80）式右边中喷管截面积的分布，那么就可以求解方程（80）来得到不同截面处喷管内的流动特性的分布P（ x），并因而反算其它流动变量。但事实上要注意，并不是给定任何一个喷管的线型，（80）式就能解出对应的流动特性P（ x），或者说（80）式并不是对于任意给定的喷管是适定的。比如当给定入口处的压力特性分别为2或2.5时，可以得到喷管截面积的分布如图7所示。可发现，当给定入口及M0后，在两相流合理的膨胀范围内，喷管具有一个最小的收缩比。如为2.5时，那么当=1.8时，喷管最小收缩比A/A0在0.4左右，如图7所示。因此当计算中给定一个喷管的最小收缩比A/A0小于0.4时，（80）式是无法给出该截面处的流动的。

图7 对于不同入口条件下的喷管收缩比的取值范围Fig.7 The convergent ratio varies in a range for different inlet conditions of the nozzle

事实上，如果一个喷管的喉部相比较于入口，非常非常之小，那么这将导致以上的气液两相流模型不再合适。因为考虑到质量流率守恒，即便单单考虑液相，其在喉部的流速也是相当地大，喉部的压力将会非常之小以至于导致空化。因此对于气液两相流动，其它非定常流动现象，比如激波可能出现；此时基于以上的定常分析将不再适合。所以，将（80）式应用于求解一个喷管内的流动时，有必要考察（80）式对该喷管是否适定。

现在利用（80）式来求解一个给定喷管内的泡状流动。喷管的基本参数为，入口高度4 cm，喉部高1.5 cm，出口高2 cm，收缩段长度7.3 cm，扩张段长度15.7 cm，入口到收缩段的等高度段长度为1 cm，喷管厚度为1.5 cm。喷管线型如图8所示。

图8 气液两相流动计算采用的喷管线型[18]Fig.8 The nozzle used for the mixture flow

Ishii[18]试验条件中入口液体质量流率为2.22 kg/s和气体质量流率为1.93×10-4kg/s，入口压力为180 kPa，温度300 K。可利用（1），（11），（16）～（18），（37），（44），（28），（30），（31）式得到以下喷管入口条件

在该入口条件下，利用（80）式算出等熵模型对喷管适定的最小收缩比为0.227 5，如图9所示。

而图8中Ishiii试验喷管的最大收缩比为0.375，大于0.235；所以（80）式在该喷管内任何截面处都适定。将图8中的喷管线型和（82）式的入口条件代入（80）式左右两端，利用非线性代数方程求解方法，就可以求得喷管各个截面上流动特性，利用（37），（71）式就可以反算出实际压力，如图10所示。与Ishii对比表明，泡状流等熵解析模型的求解的结果是可接受的。由于（82）式ω=8.7×10-6，根据（71）式可知，流动中温度变化极其微小，因此根据等温模型（66）式预测的结果也将是合理的，这里不再赘述。

图9 入口条件为（82）式时，等熵模型适定的喷管最小收缩比Fig.9 The minimum convergent ratio for the inlet condition with applying the isoentropic flow model

图10 喷管中泡状流的计算结果与试验结果[18]对比Fig.10 The comparison between the computation here and the experimental result[18]

6 结 论

本文建立了喷管中气液两相无滑移等熵流动的基本模型，并且得到了相关的解析关系。研究表明，滞止点处的体积分数决定了喷管内能达到的极限马赫数的大小，也决定了临界流动处的膨胀程度。在保持气液质量流率之比不变时，滞止点体积分数越小或压力越大，也就是气体压缩程度越大，那么流动达到极限膨胀时的马赫数就越大，流动达到临界时的压力降就越大。研究表明，气液流率之比越大，则流动中温度的变化将越明显。

基于马赫数与压力的解析关系以及质量连续方程，可以得到喷管线型与压力分布的解析解。基于该关系，给定压力分布时，可以逆向求得喷管线型，喷管喉部出现在流动马赫数为1处。在该解析解适定的喷管收缩比范围内，当给定某喷管线型时，可以相应求得该喷管内的压力分布以及其它流动特性。本文的研究结果可用于气液两相流的相关分析和设计。在雾状流动中，气液两相的滑移影响在一定程度上是不可避免的。因此将来的工作是需要在进一步考虑滑移的基础上，对气液两相的等熵流动进行进一步的理论分析。

[1]Vineet Ahujia,Ashvin Hosanadi.Analysis of the unsteady cavitation in rocket feed system and flow control elements[C]// Six International Symposium on Cavitation.Wageningen,Netherland,2006.

[2]Can F Delale,Zafer Baskaya,Steffen J Schmidt,Günter H Schnerr.Unsteady bubbly cavitating nozzle flows[C]//Proceedings of the 7th International Symposium on Cavitation,August,17-22,2009.Ann Arbor,Michigan,USA,2009.

[3]Konstantin Matveev.Ventilated waterjets for fast air cavity ships[C].Advanced Naval Propulsion Symposium American Society of Naval Engineers,2006.

[4]Amos R G,Maples G,Dyer D F.Thrust of an air-augmented waterjet[J].Journal of Hydrodynamics,1973,7(2):64-71.

[5]Varshay H,Gany A.Underwater two phase ramjet engine[P].United States Patent,1997:5598700.

[6]付英杰.水下气液两相喷射推进技术数值模拟研究[D].哈尔滨:哈尔滨工业大学,2010.

[7]董 磊.水下两相冲压式发动机数值模拟研究[D].哈尔滨:哈尔滨工业大学,2010.

[8]Glassman I.Mental combustion process[Z].American Rocket Society Preprint,1959:938-959.

[9]李 芳,张为华,张 炜,夏智勋.水反应金属燃料能量特性分析[J].固体火箭技术,2005,28(4):256-259. Li Fang,Zhang Weihua,Zhang Wei,Xia Zhixun.Analysis on energy characterisitics of hydroreactive metal fuel[J].Journal of Solid Rocket Technology,2005,28(4):256-259.(in Chinese)

[10]魏文韫.高速气雾两相流弛豫过程相间动量传递研究[D].成都:四川大学,2002.

[11]彭一川,邓安元,黄家永,李士杰.气雾两相流喷嘴的研究[J].钢铁研究,1998(3):8-11. Peng Yichuan,Deng Anyuan,Huang Jiayong,Li Shijie.Study on air-water mist jet nozzle[J].Research on Iron&Steel, 1998(3):8-11.(in Chinese)

[12]Tangren R F,Dodge C H,Seifert H.Compressibility effects in two-phas flow[J].Journal of Applied Physics,1949,20(7): 637-645.

[13]Marat Mor,Alon Gany.Analysis of two-phase homogeneous bubbly flows including friction and mass addition[J].Journal of Fluids Engineering,2004,126:102-109.

[14]Van Wijngaarden L.On the equations of motion for mixtures of liquid and gas bubbles[J].Journal of Fluid Mechanics, 1968,33(3):465-474.

[15]Eddington R B.Investigation of supersonic phonomena in a two-phase(liquid-gas)tunnel[J].AIAA,1970,8:65-74.

[16]Eddington R B.Investigation of shock phenomena in a supersonic two-phase tunnel[J].AIAA,1966,8:66-87.

[17]Thang N T,Davis M R.Pressure distribution in bubbly flow through venturis[J].International Journal of Multiphase Flow, 1981,7:191-210.

[18]Ishii R,Umeda Y,Murata S,Shishido N.Bubbly flows through a converging-diverging nozzle[J].Physics of Fluids,1993, 5(7):1630-1643.

Analytical investigation on the air-water isoentropic flows in nozzles

ZHENG Jun1,2,WANG Bao-shou2,CHEN Wei-qi2,Wang Jun-feng1,Li Chang-feng1
(1.Jiangsu University,Zhenjiang 212013,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

Based on the baratropic model and isoentropic condition of the homogeneous air-water mixture, the isoentropic model for the multiphase flow in the nozzle was established.By the ODEs of the model,the isothermal and isoentropic analytical relationships among pressure,volume fraction of air,Mach number and temperature of the mixture were obtained.The isoentropic relation indicates that the temperature varies significantly with respective to the mass flux ratio of the phases.The relation also reveals that the property at the critical point of the flow is determined by the volume fraction at the stagnation point.By the isoentropic relation above along with the mass conservation equation,a formula connecting the pressure and nozzle shape was derived,which could be used to design a nozzle by giving an anticipated pressure distribution or to calculate the flow characteristics by giving a specific nozzle shape.

air-water mixture;isoentropic flow;analytical model;limited flow;nozzle design

O35

：A

10.3969/j.issn.1007-7294.2016.10.002

1007-7294（2016）10-1219-15

2016-05-19

国家自然科学基金（11502097）；江苏省自然科学基金（BK20130478）；江苏大学高级人才科研启动基金（1281130025）

郑 俊（1983-），博士，工程师，E-mail:jszhengjun_fluid@126.com；王宝寿（1963-），男，研究员。