圆周运动的临界问题



圆周运动的临界问题

■李新国

圆周运动的临界问题涉及到力学中的几个常见力的合成问题，从圆平面的特点来看，可以将其分为水平面内和竖直平面内的圆周运动临界问题。

一、水平面内圆周运动的临界问题

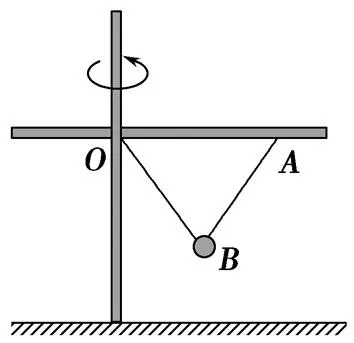
图1

例1如图1所示，水平杆固定在竖直杆上，两者互相垂直，水平杆上O、A两点连接有两轻绳，两绳的另一端都系在质量为m的小球上，OA=OB=AB，现通过转动竖直杆，使水平杆在水平面内做匀速圆周运动，三角形OAB始终在竖直平面内，若转动过程OB、AB两绳始终处于拉直状态，则下列说法正确的是()。

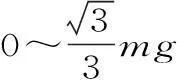
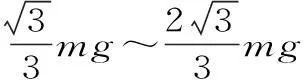
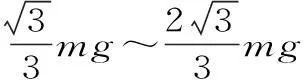
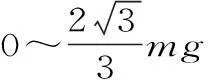
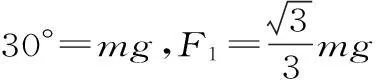
二、竖直平面内圆周运动的“轻绳、轻杆”模型

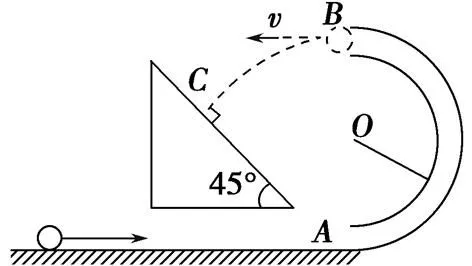
图2

例2(多选)如图2所示，一个固定在竖直平面上的光滑半圆形管道，管道里有一个直径略小于管道内径的小球，小球在管道内做圆周运动，从B点脱离后做平抛运动，经过0.3 s后又恰好垂直与倾角为45°的斜面相碰。已知半圆形管道的半径为R=1 m，小球可看作质点，且其质量为m=1 kg，g取10 m/s2。则()。

A．小球在斜面上的相碰点C与B点的水平距离是0.9 m

B．小球在斜面上的相碰点C与B点的水平距离是1.9 m

C．小球经过管道的B点时，受到管道的作用力FNB的大小是1 N

D．小球经过管道的B点时，受到管道的作用力FNB的大小是2 N

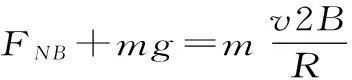
反思：竖直面内圆周运动类问题的解题技巧：(1)定模型：判断是轻绳模型还是轻杆模型，两种模型过最高点的临界条件不同。

(3)研究状态：通常情况下竖直平面内的圆周运动只涉及最高点和最低点的运动情况。

(4)受力分析：对物体在最高点或最低点时进行受力分析，根据牛顿第二定律列出方程F合=F向。

(5)过程分析：应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程。

作者单位：山东省郓城第一中学