基于字典学习的轴承早期故障稀疏特征提取

余发军, 周凤星， 严保康

(1.武汉科技大学 冶金自动化与检测技术教育部工程研究中心，武汉　430081；2.中原工学院 信息商务学院，郑州　451191)



基于字典学习的轴承早期故障稀疏特征提取

余发军1,2, 周凤星1， 严保康1

(1.武汉科技大学 冶金自动化与检测技术教育部工程研究中心，武汉430081；2.中原工学院 信息商务学院，郑州451191)

摘要：针对低速重载机械滚动轴承早期故障的振动信号中故障特征冲击成分微弱易被噪声覆盖难以识别，而利用稀疏表示方法提取冲击成分时因轴承工况非平稳性，准确匹配冲击成分字典难以构造问题，提出基于字典学习的轴承早期故障稀疏特征提取方法。利用改进型K-SVD字典学习算法构造自适应字典；采用正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)对振动信号进行稀疏分解，计算每次迭代逼近信号的峭度值，找出最大峭度值对应的逼近信号；重构特征成分并进行包络谱分析，获得故障类型。仿真及轴承振动数据测试结果表明，所提方法能更好匹配早期故障特征成分、满足轴承实时故障监测需求。

关键词：字典学习；稀疏表示；峭度值；特征提取；故障诊断

转速较低的重载机械设备(如钢包回转台、转炉等)中滚动轴承将旋转轴与轴座间滑动摩擦转化为滚动摩擦，因而承受巨大载荷。此类设备较一般旋转机械更易出现轴承故障，因此进行轴承早期故障监测与诊断对整个设备的正常运行至关重要。提取振动信号中特征成分是轴承故障诊断常用方法[1]，但因工况的复杂性所测振动信号具有非平稳性；且早期故障轴承振动信号中反映故障特征的冲击成分较微弱，极易被噪声覆盖，较难直接由时域或频域判断故障类型。小波变换[2-4]及经验模态分解方法[5-6]已成功用于轴承的早期故障诊断。而小波变换由于基与分解尺度需人为确定，缺乏自适应性；经验模态分解方法具有模式混叠劣势，难以分解窄带内的多成分信号[7]，使二者的应用受到限制。

稀疏表示方法因能将信号表示成少量原子的线性组合[8]，已成为分析非平稳信号的有力工具，且已用于滚动轴承故障诊断。如文献[9]构造参数化字典，利用粒子群优化算法对故障特征成分进行匹配追踪；文献[10]构造Gabor字典，利用相干累积量分段正交匹配追踪算法对轴承早期故障进行稀释特征提取。可见，此类方法虽能提取故障特征成分，但由于事先预定义字典缺乏对信号的自适应能力，匹配精度有待进一步提高。

基于字典学习的稀疏表示方法，先利用机器学习算法对已知信号进行训练获得自适应字典，再对测试信号在该字典上进行稀疏表示。常用字典学习算法有最优方向法(Method of Optimal Directions, MOD)[11]、K均值奇异值分解法(K-SVD)[12]等。K-SVD作为经典的字典学习算法，用稀疏表示-字典更新交互迭代两步法获得自适应字典，具有理论成熟、匹配精度高等优点，已用于语音信号增强[13]、图像去噪[14]等，但计算效率较低。

为满足故障特征提取的实时性要求，本文利用改进型K-SVD算法对字典进行学习，使构造学习型字典耗时减少。稀疏分解算法迭代终止条件是难点问题，阈值设置太小会引入噪声成分，太大会丢失有用特征成分。文献[13-14]中，虽两者使用噪声方差的倍数作为终止条件，有效抑制噪声，但实际中噪声方差事先并非已知，若用相同方法提取轴承早期故障较难实现。为此，提出利用冲击成分峭度值随噪声变化的敏感性将峭度值最大原则引入稀疏分解算法。对仿真及轴承振动数据测试结果表明，较基于参数化字典的稀疏特征提取方法，本文方法充分利用字典学习算法的自适应性，更好匹配出冲击成分，为轴承早期故障特征提取提供有效方法。

1故障特征提取的模型

信号稀疏表示指利用某种稀疏分解算法在过完备原子库(字典)中找出尽可能少的原子，使其线性组合能逼近原信号。常用稀疏分解算法有基追踪(BP)、匹配追踪(MP)、正交匹配追踪(OMP)、框架方法(MOF)等。稀疏表示方法因具有良好特性，已广泛用于信号与图像去噪、图像编码压缩与识别等。本文用信号稀疏表示对滚动轴承早期故障进行特征提取。早期故障特征成分凸显冲击性、被强噪声覆盖，先用稀疏分解算法将特征成分由噪声中提出，再分析其包络谱。

设所测振动信号为y，含故障特征成分x及高斯白噪声v，即

y=x+v

(1)

式中：x,y,v∈RN。

(2)

式中：ε为信号残差；<,>表示内积运算。

故障特征成分x具有一定结构特征，与原子库具有较强的相关性；而高斯白噪声v为随机分布，不具有结构特征，与原子库表现弱相关性[15]。因此，x由少量原子线性组合即可较好逼近，投影系数较大；而v则需较多原子才能较好逼近，投影系数较小。

以上分析知，将测量信号y在过完备字典上用匹配追踪算法进行稀疏分解时，故障特征成分x首先得到分解，而噪声v最后得到分解。若能找到判别分解x及v的分界点依据并作为稀疏分解迭代的终止条件，则可有效将特征成分x从测量信号y中提出。常用方法即将信号分解的残差与设定阈值T比较，T取1.1～1.2倍噪声方差。

(3)

实际的测量信号中噪声方差往往难以准确估计，故阈值方法作为稀疏分解迭代终止条件较难实现。峭度作为时域统计量，能描述波形尖峰程度[16]，定义为

(4)

式中：E(·)表示求均值；σ，μ分别为信号s的标准差及均值。

正常轴承振动信号服从正态分布，峭度值约为3；故障时其振动信号中瞬态冲击成分对峭度值影响较显著，其值明显大于3，谐波成分峭度值明显小于3。峭度值随噪声强度变化规律见图1，其中瞬态冲击成分幅度为1固定。由图1看出，瞬态冲击成分幅度越大，背景噪声越弱峭度值越大。因此，峭度可作为描述冲击成分显著性指标，将峭度最大原则引入稀疏分解迭代过程，可表示为

(5)

式中：K(·)表示求峭度；Γ为稀疏度；i为迭代次数。

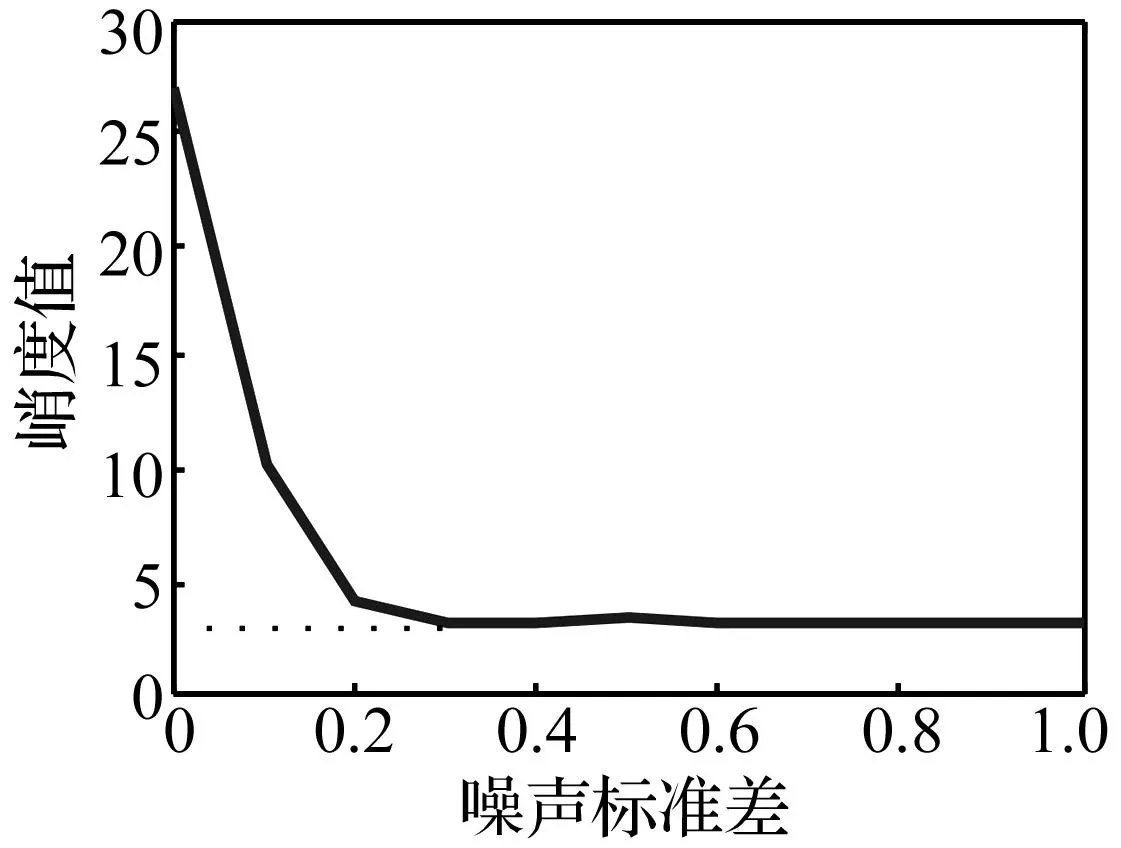
图1　冲击成分峰值为1时峭度值与噪声标准差关系Fig.1 Relationship between the changes of kurtosis value and noise standard deviation, when the peak of impulse component is 1

2故障特征提取算法

2.1改进型K-SVD字典学习

利用稀疏编码-字典更新循环迭代两步法对给定的样本信号实现自适应字典构造，较传统字典(DCT、小波基、Gabor)具有更好的自适应性及稀疏表示能力。训练时间占整个程序运行时间比重较大，不利于实时性要求高的机械设备状态监测。因此本文采用改进型K-SVD字典学习算法以提高字典学习效率。

设样本信号矩阵为Y=[y1,y2,…,ym]∈Rn×m，则字典训练算法目标函数为

(6)

式中：W=[w1,w2,…,wm]，wi(i=1,2,…,m)为样本信号yi的稀疏表示系数向量。

原K-SVD训练算法解决步骤为：①确定字典D中原子数目K及循环迭代次数J，并初始化字典D，使其每个原子具有单位2-范数；②用OMP稀疏分解算法求得系数矩阵W；③固定系数矩阵W，利用奇异值分解逐个更新每个原子，使逼近误差最小；④重复步骤②、③，直止达到预定迭代次数结束。

改进型K-SVD算法[17]在步骤③中不再对全部字典基使用奇异值分解，而据迭代中字典索引集合元素个数选择更新方式。改进做法如下：

(1)随机排列字典序号，即rperm=randperm(K)，初始化计数器j=1及集合U={1,2,…,m}。

(2)若j=K成立跳至步骤(5)，否则令h=rperm(j)，找出系数矩阵W第h行向量中元素不为0的序号集合Ih={l |W(h,l )≠0}。

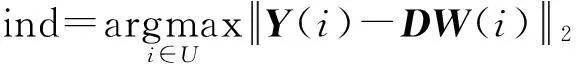
(7)

更新D(h)=d及{W(h,l )|l∈Ih}=p。

(4)更新计数器j=j+1，转至步骤(2)。

(5)据字典D中各原子互相关系数整理字典，并输出整理的字典D。

由此知改进后K-SVD算法与原算法主要区别在于：①改进后随机排列字典，而原算法按顺序更新字典；②改进后算法只需据集合Ih非零元素个数对部分字典基进行奇异值分解，减少计算量，而原算法需对全部字典基进行奇异值分解。

2.2特征成分提取

自适应字典D获得后先对长度为N的原始测量振动信号y进行矩阵化处理，即按步长Δn重叠分割y成P个列信号y1,y2,…,yP组成矩阵Y，每个列信号长度为n，再用OMP求解对应的稀疏系数矩阵W。实施OMP过程中对列信号yi(i∈{1,2…,P})先设定总迭代次数为字典D原子数的1/2，每次迭代找到一个最佳原子逼近剩余信号，计算逼近信号峭度，总迭代结束后找出峭度最大值对应的迭代次数及逼近信号，并将对应的稀疏系数向量作为W的列向量wi，其它列信号处理方法相同。

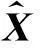
(8)

式(8)为二次优化问题，可以转化为

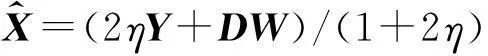
(9)

式中：η为惩罚系数。

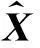
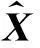
3仿真测试

仿真信号含周期冲击及噪声成分。每个周期内冲击函数为exp(-100t)cos(300πt)，重复频率10 Hz，叠加高斯白噪声，使信噪比为0 dB，采样频率1 000 Hz，采样点1 000。

利用本文方法对染噪信号进行冲击成分提取。在字典训练阶段将未染噪信号按步长2重叠分割作为样本信号矩阵，令每个样本长度分别为8、16、32、64、128，考察不同样本长度影响。令字典中原子个数为样本信号数的1/2倍，以随机数初始化字典，使每个原子具有单位2范数，训练次数20，训练结束条件为误差值10-5。不同样本长度下用改进型K-SVD算法所得字典重构未染噪信号信噪比为

(10)

式中：s0，s分别为未染噪信号及重构信号。

不同样本信号长度的训练效果见图2。由此看出，样本长度为32点时信噪比最大。

图2　不同样本信号长度训练效果Fig.2 Training effects with the different lengths of sample signal

改进型K-SVD算法与原K-SVD算法训练字典所需时间见表1(7.0.0版Matlab运行在CPU主频为3.6 GHz、内存为4 GB的PC机)，可见改进后训练时间明显缩短。

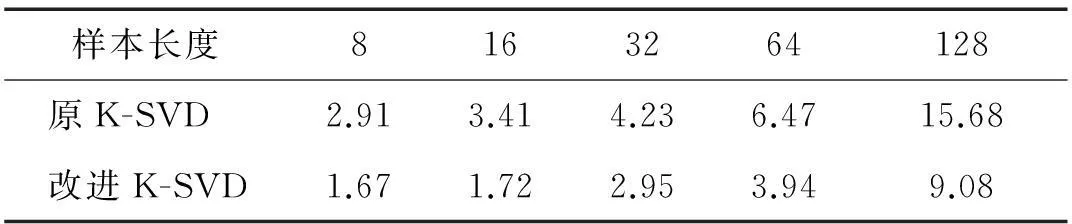
表1　两种训练算法所用时间

本文方法在稀疏编码阶段将信噪比为0 dB的仿真信号按步长2重叠分割成信号矩阵，使每个列信号长度为32点。利用字典训练阶段所得原子长度32字典对该信号矩阵进行OMP分解。令总迭代次数为字典中原子总数的1/2, 计算每次迭代逼近信号峭度，找出各列信号最大峭度对应稀疏系数向量及逼近信号。各列信号最大峭度值及对应的迭代次数(即稀疏度)见图3。由图3看出，各列信号只需2个原子的线性组合即可较好重构。

图3　各列信号最大峭度值及分解的稀疏度Fig.3 The maximum kurtosis values of column signals and their sparsities of decomposition

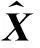
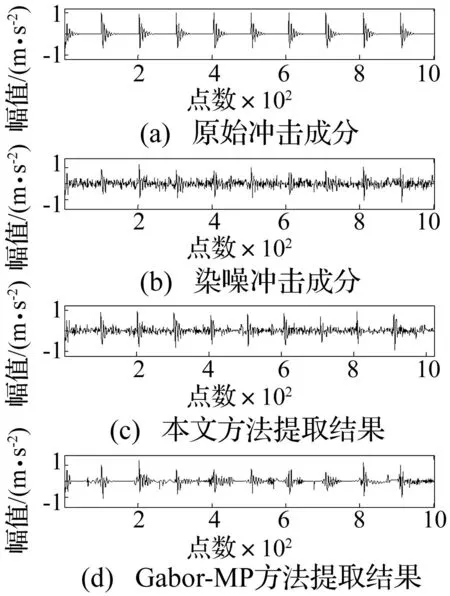
图4　两种方法提取的冲击成分Fig.4 The impulse components extracted by two methods

原始冲击染噪冲击本文方法Gabor-MP方法峭度值16.436.2315.0313.87

4实验测试

为进一步验证所提方法的有效性，用旋转机械振动故障试验平台模拟低速重载机械中轴承早期故障。试验平台主要由调速电机、传动轴、轴承支架、模拟负载及数据采集等组成。其中数据采集由压电加速度传感器及信号采集器完成。选型号N205EM的轴承(外径52 mm、内径25 mm、滚动体数12、滚动体直径7.5 mm、接触角0°)为实验对象，设轴承转速为300 r/min，负载为重载工况，振动数据采样频率20 kHz。

先对该型号正常轴承1的振动数据进行采样，获得Norm1数据；取下该轴承并在外环加工一凹点故障，设转速、负载同前，得Outer数据；取下该外环故障轴承，安装该型号正常轴承2进行采样，获得Norm2数据；取下轴承2并在内环加工一凹点故障，设相同转速、负载试验，采样获得Inner数据。

正常轴承振动数据中无冲击，但会含由轴承钢性非线性、滚动体承载非线性等因素导致的干扰源[18]；工况相同条件下该轴承外环或内环故障的振动数据中除干扰源外亦含周期冲击成分，为两者的叠加。因此利用本文方法对两种故障进行特征提取时，在字典训练阶段以Outer数据与Norm1数据差值为外环训练样本信号，以Inner与Norm2数据差值为内环训练样本信号。各取对应的1 s时间段数据(即20 000采样点)，4段信号见图5。

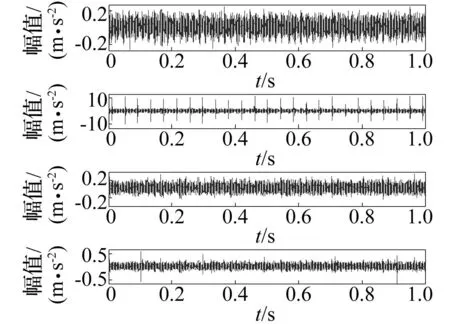
图5　四段轴承振动信号Fig.5 The four vibration signals of bears

将两差值信号(Outer-Norm1及Inner-Norm2) 按步长2重叠分割作为样本信号矩阵，令每个样本长度分别为8、16、32、64、128，令字典中原子个数为16，以随机数初始化字典，使每个原子具有单位2范数，训练次数20，训练结束条件为误差值10-5。用改进型K-SVD训练后以SNR为衡量指标，外环、内环最佳样本长度(原子长度)均为64，训练的外环、内环字典见图6。

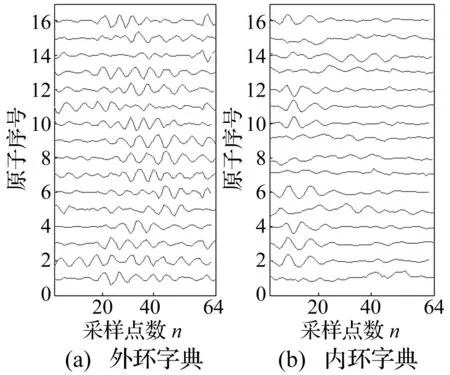
图6　改进型K-SVD算法训练的字典Fig.6 The obtained dictionaries learned by the developed K-SVD algorithm

外环、内环字典获得后将Outer、Inner数据按步长2重叠分割成各自信号矩阵，每个列信号长度为64点，分别利用外环、内环字典对各自信号矩阵进行OMP分解，并令总迭代次数为字典中原子总数的1/2, 计算每次迭代逼近信号峭度，找出各列信号最大峭度对应稀疏系数向量及逼近信号。将各列信号稀疏系数向量组成矩阵，令惩罚系数η范围[0,1]，递增值为0.1，搜索连接列信号峭度值最大时对应的η。外环当η= 0.2时连接列信号峭度值最大，波形见图7(a)，对应的包络谱见图8(a)；内环当η=0.3时连接列信号的峭度值最大，波形见图9(a)，对应的包络谱见图10(a)。

本文用Gabor-MP方法对Outer、Inner数据进行故障特征提取，分别见图7(b)、图9(b)，对应的包络谱见图8(b)、图10(b)。由此可见，两种方法均能识别特征频率为fo=24.3 Hz的外环故障，但特征频率为fi=35.7 Hz的内环故障Gabor-MP方法不能准确提取，而本文方法能准确提出，优势明显。

图7 两种方法提取的外环故障特征成分Fig.7Theouter-racefaultfeaturecomponentextractedbythetwomethods图8 外环故障特征成分包络频谱Fig.8Theenvelopespectrumoftheouter-racefaultfeaturecomponentd图9 两种方法提取的内环故障特征成分Fig.9Theinner-racefaultfeaturecomponentextractedbythetwomethods

图10　内环故障特征成分包络频谱Fig.10 The envelope spectrum of the inner race fault featurecomponent

5结论

(1)基于字典学习的轴承早期故障稀疏特征提取方法利用改进型K-SVD字典学习算法构造出能准确匹配特征成分的字典，在稀疏分解过程中，通过计算每次迭代后逼近信号的峭度值，找出峭度值时对应的逼近信号，能自适应确定出特征成分与噪声成分的稀疏表示分解点。

(2)通过与参数化Gabor字典相比，基于字典学习的稀疏特征提取方法能准确提取强噪声背景下内外环故障特征成分，其波形与原波形更接近，失真更小。

参 考 文 献

[1] 刘永斌．基于非线性信号分析的滚动轴承状态监测诊断研究[D]．合肥：中国科学技术大学，2011：8-9．

[2] Lin J, Qu L. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis[J]. Journal of Sound and Vibration, 2000, 234(1):135-148.

[3] Wang S B, Huang W G, Zhu Z K. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis[J].Mechanical Systems and Signal Processing,2011, 25(4):1299-1320.

[4] Kankar P K, Sharma S C, Harsha S P. Fault diagnosis of rolling element bearing using cyclic autocorrelation and wavelet transform[J]. Neurocomputing, 2013, 110 :9-17.

[5] Cheng J S, Yu D J, Tang J S, et al. Application of frequency family separation method based upon EMD and local Hilbert energy spectrum method to gear fault diagnosis[J]. Mechanism and Machine Theory, 2008, 43:712-723.

[6] Li Y J, Tsea P W, Yang X. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engineer[J].Mechanical Systems and Signal Processing, 2010, 24:193-210.

[7] Peng F Q, Yu D J, Luo J S. Sparse signal decomposition method based on multi-scale chirplet and its application to the fault diagnosis of gearboxes[J]. Mechanical Systems and Signal Processing,2011, 25:549-557.

[8] Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing,1993, 41(12): 3397-3415.

[9] Wang Xin-qing, Zhu Hui-jie, Wang Dong. The diagnosis of rolling bearing based on the parameters of pulse atoms and degree of cyclostationarity[J]. Journal of Vibroengineering, 2013, 15(3):1560-1575.

[10] 严保康，周凤星. 基于相干累积量正交匹配追踪算法的轴承早期故障稀疏特征提取[J]. 机械工程学报，2014,50(13):88-94.

YAN Bao-kang, ZHOU Feng-xing.Initial fault identification of bearing based on coherent cumulant stagewise orthogonal matching pursuit[J]. Journal of Mechanical Engineer,2014, 50(13):88-94.

[11] Engan K, Aase S O, Husoy J H. Method of optimal directions for frame design[J].Proceedings ICASSP’ 99-IEEE International Conference on Acoustics, Speech, and Signal Processing, 1999,5:2443-2446.

[12] Aharon M, Elad M, Bruckstein A M.The K-SVD: an algorithm for designing of overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006, 54(11): 4311-4322.

[13] Zhou Yan, Zhao He-ming, Shang Li. Immune K-SVD algorithm for dictionary learning in speech denoising[J]. Neurocomputing, 2014, 137:223-233.

[14] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing,2006,15(12):3736-3745.

[15] 王国栋,阳建宏,黎敏,等. 基于自适应稀疏表示的宽带噪声去除算法[J]. 仪器仪表学报, 2011,32(8): 1818-1823.

WANG Guo-dong, YANG Jian-hong, LI Min, et al. Wideband noise removing algorithm based on adaptive sparse representation[J]. Chinese Journal of Scientific Instrument, 2011,32(8): 1818-1823.

[16] 苏文胜,王奉涛,张志新．EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]．振动与冲击，2010，29(3)：18-22．

SU Wen-sheng,WANG Feng-tao,ZHANG Zhi-xin．Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock,2010,29(3):18-22．

[17] 李洋,李双田. 压缩感知下的稀疏表示语音恢复模型与算法[J].信号处理,2014,30(8):914-923.

LI Yang, LI Shuang-tian. Speech recovery model and algorithm over sparse representation based on compressive sensing[J].Journal of Signal Processing,2014,30(8):914-923.

[18] 苗中华,周广兴,刘海宁,等.基于稀疏编码的振动信号特征提取算法与实验研究[J].振动与冲击,2014,33(15):76-81.

MIAO Zhong-hua,ZHOU Guang-xing, LIU Hai-ning, et al. Tests and feature extraction algorithm of vibration signals based on sparse coding[J].Journal of Vibration and Shock, 2014,33(15):76-81.

Bearing initial fault feature extraction via sparse representation based on dictionary learning

YUFa-jun1,2，ZHOUFeng-xing1，YANBao-kang1

(1.Metallurgical Automation and Detection Technology ERC of Education Ministry, Wuhan University of Science and Technology, Wuhan 430081,China;2.College of Information & Business, Zhongyuan University of Technology, Zhengzhou 451191,China)

Abstract:As initial fault occurs in rolling bearings of low-speed and heavy-duty machinery, the impulse component, reflecting the fault feature in vibration signals is difficult to extract because it is relatively weak and easily corrupted by strong background noise. The authors attempted to extract the impulse component from a vibration signal with the sparse representation method. However, it is difficult to construct an accurate dictionary that matches the impulse component since operation conditions of bearing are not stable. Hence, a method of extracting the initial fault feature, which is based on dictionary learning, was proposed in this research. Firstly, an adaptive dictionary was obtained by the developed K-SVD dictionary-learning algorithm. Then, Orthogonal Matching Pursuit (OMP) algorithm was utilized for sparse decomposition of the vibration signal, and all kurtosis values of approximation signal of iterations were calculated. Finally, the corresponding approximation signal of maximal kurtosis value was reconstructed and analyzed with the envelope spectrum to diagnose the fault type. The test results of simulated data and bearing vibration signals demonstrate that the proposed method, which can extract the feature component more accurately than other methods, meets the demand of real-time bearing condition monitoring.

Key words:dictionary learning; sparse representation; kurtosis value; feature extraction; fault diagnosis

中图分类号:TN911；TH17

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.033

通信作者周凤星 男，教授，博士生导师，1952年10月生

收稿日期：2014-12-17修改稿收到日期：2015-04-10

基金项目：国家自然科学基金项目(61174106)；河南省高等学校重点科研项目(15B510017)

第一作者 余发军 男，博士，讲师，1981年6月生

E-mail：blackghostpeter@163.com