受静压力作用加筋板隔声性能研究

孙勇敢， 黎　胜

(1.大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部 船舶工程学院，辽宁 大连　116024；2.重庆交通大学 航海学院，重庆　400074)



受静压力作用加筋板隔声性能研究

孙勇敢1.2， 黎胜1

(1.大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部 船舶工程学院，辽宁 大连116024；2.重庆交通大学 航海学院，重庆400074)

摘要：基于随机入射平面波建立混响声场激励的加筋板隔声计算模型，通过对试验模型数值计算，二者结果基本吻合；计算存在静压力时加筋板隔声特性表明，存在静压力时加筋板基频移动会致低频隔声量显著增加，压力增加到一定程度时隔声量基本不再增加；此可为存在预应力的实际结构物隔声量计算提供参考。

关键词：加筋板；隔声量；混响声源 ；静压力

由于受水或货物的静压力、热效应、焊接应力等作用，舰船等海洋结构会存在附加预应力，研究含预应力的典型结构声振特性及隔声特性具有重要理论意义及实际价值。对结构声振特性，实验表明初始应力对结构动态特性有一定影响[1]。Zhou等[2-3]对潜浮状态的圆柱壳结构声振特性进行研究，分析组合边界特性的声辐射特点及边界特性、深水中静压力对结构声辐射、动力响应影响。Iakovlev等[4]研究受静压力作用的圆柱壳结构振动声辐射特性。Zhou等[5]分析加筋圆柱壳结构受不同静水压力作用的结构动态响应及功率流。陈炉云等[6]用变分原理推导含局部预应力的圆柱壳结构动力响应方程，对比预应力对声辐射功率及声指向性影响表明，局部预应力存在对声辐射影响较大，尤其低频率段更明显；局部预应力对结构声辐射指向性也具明显影响。对隔声性能，Liu等[7-9]对舰船等海洋结构物典型结构如加筋板结构、夹芯板、复合板隔声性能进行深入研究，但对含预应力结构的隔声性能研究较少[10]。

本文针对受均布压力作用的加筋板隔声量计算问题，基于随机入射平面波建立混响声场激励的加筋板隔声量计算模型，研究低频时不同静压力对加筋板隔声量影响。

1静压力作用下加筋板隔声性能计算模型

1.1静压力作用下加筋板刚度矩阵

加筋板离散结构单元采用文献[11]的板单元，无压力时加筋板单元刚度矩阵为

[ke]=∬[G]T[H][G]dxdy

(1)

式中：[G]为单元应变矩阵；[H]为弹性矩阵。

总体刚度矩阵为

(2)

单元等效节点载荷为

{P}e=∬[N]T{p}ds

(3)

式中：[N]为形函数矩阵；p为作用于加筋板面板的压力。

全部节点载荷组成的向量为

{P}=∑{P}e

(4)

加筋板结构平衡方程组为

[K]{δ}={P}

(5)

式中：{δ}为全部节点位移组成的向量。

加筋板结构单元位移为

{δ}e=[T]T{δe}

(6)

式中：[T]为坐标转换矩阵；{δ}e,{δe}为局部、总体坐标系下单元位移向量。

{σ}=[S]{δ}e

(7)

式中：[S]为应力矩阵；{σ}=[Nx,Ny,Nxy]T。

存在静压力时加筋板单元刚度矩阵改变量为

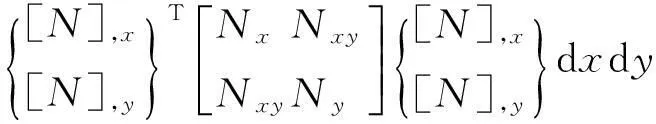
(8)

无压力及存在静压力时加筋板整体刚度矩阵改变量分别为

(9)

1.2静压力作用下加筋板隔声量计算

为建立混响声场，用多个随机入射角、振幅、相位角的平面波相互叠加[12-13],设第n个平面声波以角度(θn,φn)入射，见图1、图2，其表达式为

pn(x,y,z;t)=Pcos(θn)e-i(kxx+kyy+kzz)ei(wt+βm)

(10)

式中：kx,ky,kz分别为该平面波在x,y,z三方向波数；w为平面声源简谐振动圆频率；βm为随机相位角，均匀分布于[0,2π]区间；θn为入射角，均匀分布于[-π,π]区间；pcos(θn)为平面波振幅法向分量，pn均匀分布于[0,1]区间。

设平面波做简谐振动，则空间均布声压为

(11)

N个平面波作用于结构单元中心的有效声压为

(12)

混响声源产生的入射声功率[14]为

(13)

式中：S为结构表面积；ρ0为空气密度；c为空气声速。

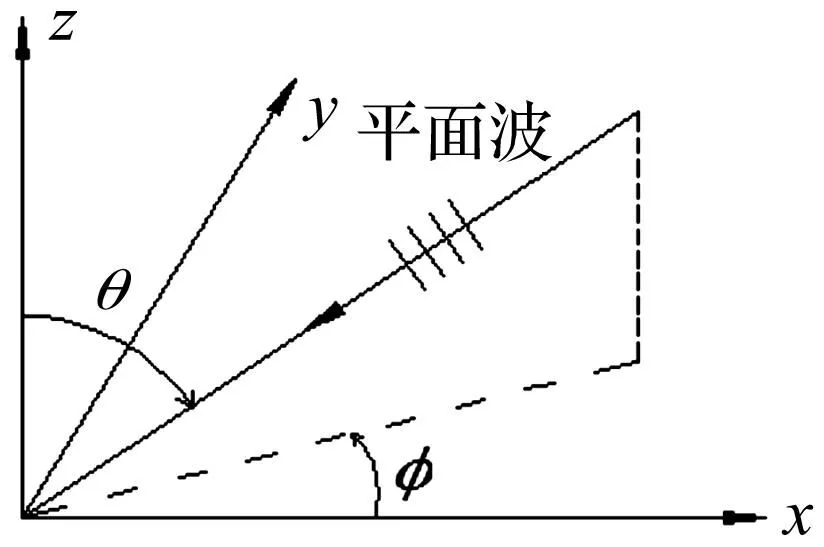
图1　任一平面波以角度(θ,φ)入射加筋板Fig.1 Random plane wave incident on a panel at angles(θ,φ)

图2　任一平面波入射加筋板Fig.2 Random plane wave incident on the stiffened panel

加筋板在混响声源作用下有限元形式运动方程为

(14)

式中：u(ω)为结构节点速度向量；[M]为结构质量矩阵；[C]为结构阻尼矩阵；[Ks]=[K]+[ΔK]为静压力下整体刚度矩阵，[K]为无压力时整体刚度矩阵，[ΔK]为由静压力引起的结构整体刚度矩阵改变量。

令[B]=-ω2[M]+iω[C]+[K]，结构速度列向量为

(15)

由结构表面法向振速列向量vn与速度列向量v关系得

(16)

式中：[D]为节点速度与法向速度的转换矩阵。

由图3，瑞利积分得空间中一点A的声压为

(17)

对式(17)进行离散得

(18)

式中：下标m表示第m个结构单元；N为单元总数；Am为第m个单元面积；Rm为第m个单元中心与空间中一点距离；vm为第m个单元法向振速。

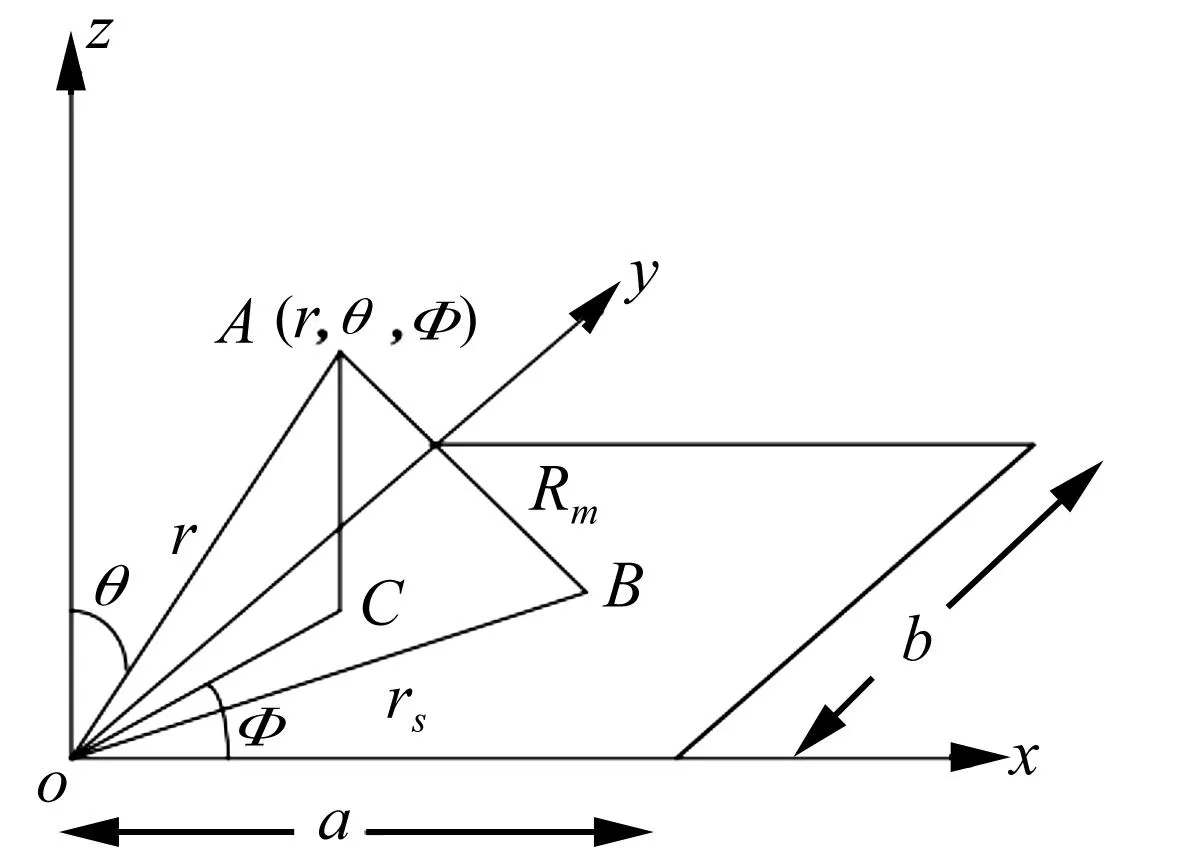
图3　瑞利积分坐标Fig.3 Rayleigh integral coordinates

结构声辐射声强[15]为

(19)

对包络半圆球面单元声强与相应单元面积乘积求和，得结构辐射声功率为

(20)

对混响声源激励作用的加筋板隔声量定义为

(21)

定义给定频率段加筋板隔声量[16]为

(22)

式中：f1，f2为下、上限频率。

建立加筋板在混响声源激励下的隔声量计算模型见图4。

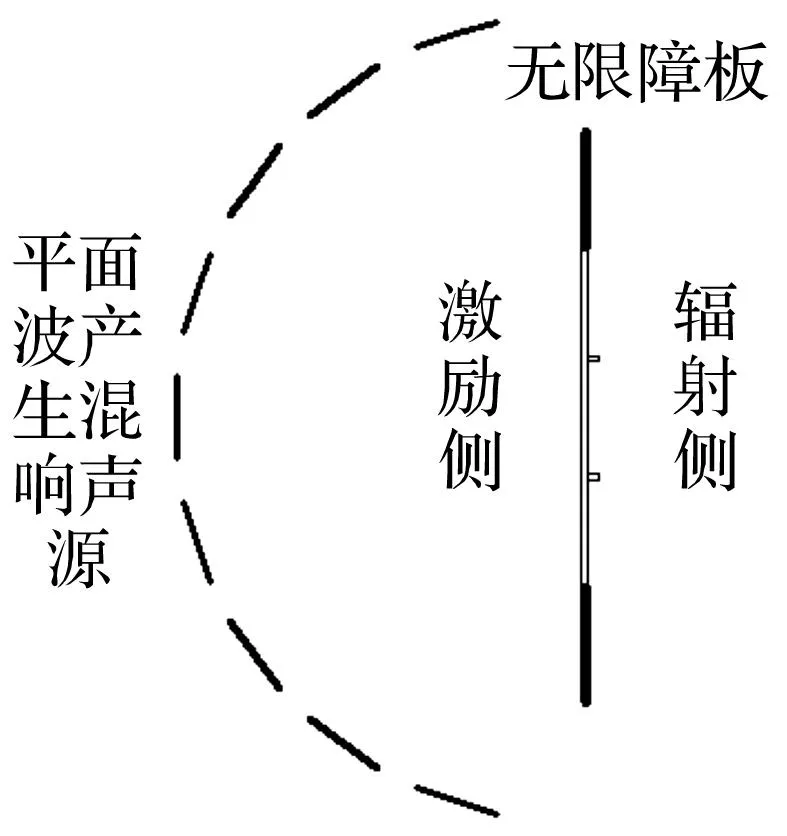
图4　混响声源作用下隔声计算模型Fig.4 A model for the transmission loss of diffuse sound

2加筋板结构隔声性能数值结果分析

加筋板结构模型见图5，长a=0.8 m，宽b=0.8 m，厚h=0.005 m，筋骨厚w=0.005 m，筋骨高H=0.015 m，钢材密度ρs=7 850 kg/m,弹性模量Es=2.1×1011kN/m2，泊松比0.3；铝材密度ρa=2 700 kg/m，弹性模量为Ea=7×1010N/m2，泊松比为0.346；空气密度为ρ空=1.21 kg/m3，c空=343 m/s；参考声功率取10-12W，入射平面波数N=1 145。数值计算中有限元离散结构用文献[11]板元，网格尺寸0.2 m×0.2 m，全文中板材四边边界均用自由边界条件并对所有节点运动限制在z向。

图5　加筋板结构模型Fig.5 A model for Stiffened plate

2.1模型验证

为验证本文数值模型可靠性，对试验模型[17]进行数值计算。采用9个均匀分布的喇叭建立混响声场，试验所用模型为铝板，尺寸0.457 m×0.457 m，厚0.000 8 m，静压力取0 Pa及6.9 kPa，数值验证用9个随机入射平面波建立混响声场激励。数值计算与试验结果对比知，在20～300 Hz频率段二者基本吻合，见图6。

图6　有限元瑞利积分模型与试验结果比较Fig.6 Comparison between FEM-Rayleigh model and experiment results of model

2.2存在静压力时加筋板隔声量计算

低频噪声对生活及健康影响较大，国际低频噪声上限为100 Hz[18]，由于其波长较长，穿越墙或板时声波衰减较小，因此控制噪声为治理难题之一。

本文对加筋板低频隔声量进行研究。该板四边自由支持，材料分别为钢材、铝。不同压力作用的(板上均布压力为0 atm、1 atm、2 atm)隔声量曲线见图7、图8，加筋板在真空中的固有频率见表1。

由表1看出，存在静压力时加筋板固有频率相应增加，尤其第一阶频率增幅最大。由图7、图8看出，因第一阶频率增加使加筋板隔声曲线向高频方向移动，低频时(25～100 Hz)加筋板隔声量显著增加。钢加筋板存在1 atm压力时其隔声量平均增加7 dB，近似估算出静压力0～1 atm时加筋板隔声量增加的平均速率为0.7 dB/0.1 atm；压力增至2 atm时其隔声量平均增加16 dB，可近似估算出静压力1～2 atm时加筋板隔声量增加的平均速率为1.6 dB/0.1 atm。铝加筋板受1 atm压力时其隔声量平均增加15 dB，可近似估算出静压力0～1 atm时加筋板隔声量增加的平均速率为1.5 dB/0.1 atm；压力增至2 atm、低频时隔声量平均增加5 dB，近似估算出静压力1～2 atm时加筋板隔声量增加的平均速率为0.5 dB/0.1 atm。因此计算航空或水下结构物噪声时可计算若干典型压力下结构隔声量曲线，并据实际情况对隔声量曲线进行修正，使结果较合理。

图7　不同压力下钢加筋板隔声量曲线Fig.7 Predicted different pressure influence on TL(steel)

图8 不同压力下铝加筋板隔声量曲线Fig.8 Predicted different pressure influence on TL(aluminum)

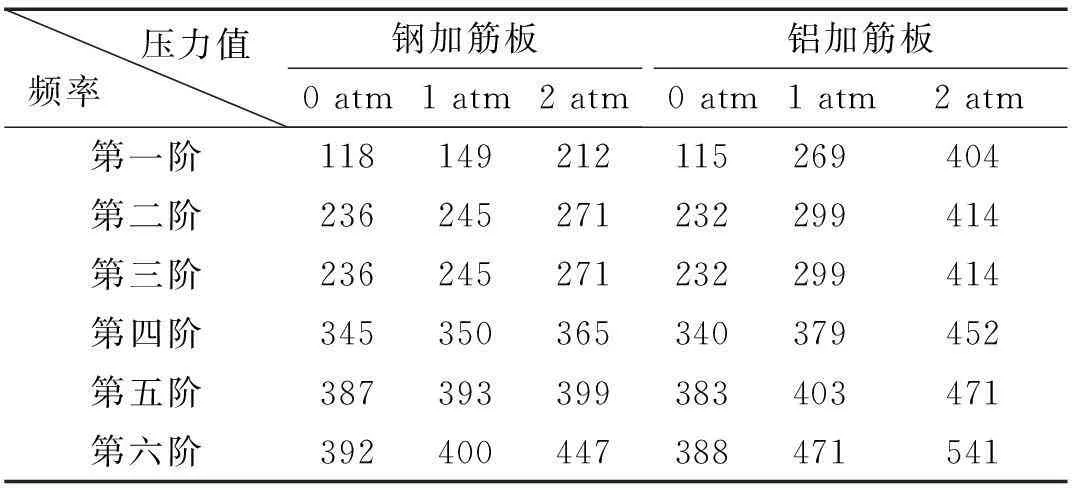
压力值频率钢加筋板0atm1atm2atm铝加筋板0atm1atm2atm第一阶118149212115269404第二阶236245271232299414第三阶236245271232299414第四阶345350365340379452第五阶387393399383403471第六阶392400447388471541

低频时(25～100 Hz)不同压力下加筋板平均隔声量见图9、图10。由两图看出，压力从1 atm增加到2 atm时钢加筋板平均隔声量增幅最大；压力从0 atm增加到1 atm时铝加筋板平均隔声量增幅最大。因此，无论钢板或铝板，压力从2 atm再增加时平均隔声量均增加较小，说明不同材料加筋板隔声量对压力敏感度不同。

图9　不同压力下钢加筋板平均隔声量Fig.9 Different pressure influence on STLoverall(steel)

图10　不同压力下铝加筋板平均隔声量 Fig.10 Different pressure influence on STLoverall(aluminum)

3结论

通过基于随机入射平面波建立混响声场激励下加筋板隔声数值计算模型，计算不同压力、不同材料加筋板隔声量曲线，结论如下：

(1)压力使加筋板基频向高频方向移动，低频时易增加加筋板隔声量。

(2)加筋板有压力时隔声量显著增加，压力增加到一定程度再增加时，隔声量几乎不再增加；不同材料加筋板隔声量对压力敏感度不同。

(3)计算航空或水下结构物噪声时，可计算若干典型压力下隔声量曲线，据实际情况对隔声量曲线进行修正，可获得较合理结果。

参 考 文 献

[1] Parker R G, Mote Jr C D. Tuning of the natural frequency spectrum o f air circular plate by in-plane stress[J].Journal of Sound and Vibration,1991,145 (1) : 95-110.

[2] Zhou Q, Joseph P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration, 2005, 283(3/4/5): 853-873.

[3] Ye W N，Li T Y，Zhu X .The vibro-acoustic characteristics of the cylindrical shell partially submerged in the fluid[J]．Applid Mechanics and Materials,2012,170/171/172/173(5):2303-2311.

[4] Iakovlev S, Dooley G, Williston K, et al. Evolution of the reflection and focusing patterns and stress states in two-fluid cylindrical shell systems subjected to an externl shockwave[J] .Journal of Sound and Vibration,2011,330(25):6254-6276.

[5] Zhou Xin-ping.Vibration and stability of ring-stiffened thin walled cylindrical shells conveying fluid[J].Acta Mechanica Solida Sinica,2012,25(2):168-176.

[6] 陈炉云,李磊鑫,张裕芳.局部预应力的圆柱壳结构声辐射特性分析[J].上海交通大学学报,2014,48(8):1084-1089.

CHEN Lu-yun, LI Lei-xin,ZHANG Yu-fang. Characteristics analysis of structural acoustic of cylindrical shell with prestress in local areas[J]. Journal of Shanghai Jiaotong University,2014,48(8):1084-1089.

[7] Liu B, Feng L, Nilsson A C. Sound transmission through curved aircraft panels with stringer and ring frame attachments [J].Journal of Sound and Vibration, 2007, 300(3/4/5):949-973.

[8] 黎胜,赵德有.平面声波由空气经加肋板向水中传输的数值计算研究[J].声学学报,2002, 27 (2): 112-116.

LI Sheng, ZHAO De-you. Numerical analysis of sound transmission of an incident plane wave from air to water through stiffened plates [J].Acta Acustica,2002,27(2): 112-116.

[9] Campolina B,Atalla N,Dauchez N,et al.Four-pole modellingof vibration isolators: application to SEA of aircraft double-wall panels subjected to mechanical excitation[J]. Noise Control Engineering Journal, 2012, 60(2):158-170.

[10] Liu B, Feng L, Nilsson A C. Influence of overpressure on sound transmission through curved panels[J].Journal of Sound and Vibration, 2007,302(4/5):760-776.

[11] 母德强,陈塑寰,冀清发.初应力对薄板动态特性影响的理论计算分析与研究[J].吉林工学院学报,1996,17(3):1-5.

MU De-qiang,CHEN Su-huan,JI Qing-fa.The influence of initial stress on the vibrational behavior of thin platesa theoretical analysis and study[J].Journal of Jilin Institute of technology,1996,17(3):1-5.

[12] Rafaely B. Spatial-temporal correlation of a diffuse sound field[J]. Journal of Acoustical Society of America,2000, 107(6): 3254-3258.

[13] Josshi P, Mulani S B, Kapania R K. Multi-objective vibroacoustic optimization of stiffened panels excited by acoustic diffuse field[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structural, Structural Dynamics and Materials Conference,Denver, Colorado,2011.

[14] Schaffer H, Pucher E. Methods to simulate airborne sound transmission at railway door panels with deterministic wave[J].Journal of Materials Science and Engineering,2013,A3(11):775-791.

[15] Fahy F. Sound and structural vibration[M].New York: Academic Press, 1985.

[16] Ou D Y, Mak C M, D S M. Prediction of the sound transmission loss of a stiffened window[J].Journal of Building Services Engineering Research & Technology, 2012,34(4): 359-368.

[17] Roskam J, Dam C V, Grosveld F. Some noise transmission loss characteristics of typical general aviation structural materials [C]//AAIA Aircraft Systems and Technology Conference,Los Angeles,1978.

Sound transmission through stiffened plates under static pressure

SUNYong-gan1,2，LISheng1

(1.State Key Laboratory of Structural Analysis for Industrial Equipment, School of Naval Architecture, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, China;2. Maritime College, Chongqing Jiaotong University, Chongqing 400074, China)

Abstract:Based on the concept of plane wave propagation, a model of sound transmission through stiffened plates excited by an acoustic diffuse field under static pressure was developed. Simulation results based on the model structure are very close to experiment results in the literature. Sound transmission through stiffened plates under static pressure was then investigated. The results show that static pressure may cause the base frequency of the stiffened plate to shift and lead to transmission loss at low frequencies. When the pressure increases to a certain level, the sound transmission loss is no longer increasing.The results might contribute to the literature of sound transmission computation through structures with initial stresses.

Key words:stiffened plates; sound transmission loss; acoustic diffuse field; static pressure

中图分类号:U661.44

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.031

通信作者黎胜 男，博士，教授，1973年生

收稿日期：2015-02-28修改稿收到日期：2015-04-01

基金项目：辽宁省教育厅重点实验室基础研究项目(LZ2014004)

第一作者 孙勇敢 男，博士生，1985年生