基于字典学习和结构聚类的图像去噪算法研究

潘慧+霍智勇++陈诗雨++程成

摘要：针对K-SVD算法和BM3D算法的不足，本文提出了基于字典学习和结构聚类的图像去噪算法。该算法首先通过字典学习得到含噪图像的冗余字典，然后对相似的图像块进行聚类构成块群，并通过迭代收缩和L1正则化约束，对同类的图像块在字典上进行稀疏表示，以达到降噪的目的。实验结果表明，在常规的图像处理上，本文提出的算法能较好的保留图像的结构信息，与K-SVD和BM3D等现有的流行算法相比，具有更高的峰值信噪比（PNSR）。

关键词：字典学习；结构聚类；图像去噪；稀疏表示

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2016）14-0155-04

Research in Image Denoising Algorithm based on Dictionary Learning and Structural Clustering

PAN Hui， HUO Zhi-yong， CHEN Shi-yu， CHENG Cheng

（Nanjing University of Posts and Telecommunications， Nanjing 210046， China）

Abstract： For the purpose of overcoming the weak points of K-SVD algorithm and BM3D algorithm， we propose the image denoising algorithm based on dictionary learning and structural clustering.It firstly get the redundant dictionary of a noised image by dictionary learning.Then，the image patches are gathered according to their similarities.Meanwhile，the similar patches get sparse representation showed in dictionaries by iterative shrinkage and L1 regularization constraints and eventually the image is restored and noise is removed.The experimental results indicate that the proposed algorithm can well preserve the structure information of the common image with a higher Peak Signal to Noise Ratio（PNSR），compared with state-of-the-art algorithms，such as K-SVD and BM3D.

Key words： dictionary learning；structural clustering；image denoising；sparse representaion

在传输和接收图像的过程中，由于噪声的干扰，常常会导致图像的结构信息被破坏、清晰度降低、图像质量下降等问题。因此，图像去噪一直是图像处理领域的重点研究对象。

针对图像去噪的正则化问题有局部和非局部两种去噪算法。局部去噪算法表明：在希尔伯特空间（字典[Φ∈Rn×m]）中，一个信号[x∈Rn]可被分解为一个n维向量集合，即[xn×1=Φn×mαm×1]，其中[α]代表权重向量，[α]的稀疏性可由它的L0范数或更易计算的L1范数描述[1]，这种研究涉及了基函数的构造，字典的自适应学习（例如：K-SVD[2][3]，以及随机逼近[4]）。非局部去噪算法表明：自然图像含有自重复模式，利用重叠块的自相似性可以得到许多非局部图像去噪算法——例如，非局部中值[5]，BM3D[6][7]，局部学习字典K-LLD[8]（locally learned dictionaries），LSSC[9]（learned simultaneous sparse coding）。在这一系列的算法中，K-SVD算法和BM3D算法一直拥有较高的峰值信噪比（Peak Signal to Noise Ratio，PNSR）。因此，我们认为，联合稀疏性与聚类性可能会更有效的解决图像去噪问题。

由此，本文提出了基于字典学习和结构聚类的图像去噪算法。该算法提供了一种新模型——基于聚类的稀疏表示（clustering-based sparse representation，CSR）。CSR模型的基本思想是把局部和非局部稀疏约束视作同类，即合并字典学习和结构聚类。首先通过字典学习得到含噪图像的冗余字典，然后对图像块进行相似性的计算，并据此对图像块进行聚类，随后通过迭代收缩和L1正则化约束，对同类的图像块在字典上进行稀疏表示，从而达到降噪的目的。实验结果表明，在常规的图像处理上，本文提出的算法能较好的保留图像的结构信息，与K-SVD和BM3D等现有的流行算法相比，具有更高的峰值信噪比（PNSR）。

1 基于聚类的稀疏表示基本思想

1.1基于聚类的稀疏表示模型

沿用参考文献[2]中使用的符号格式，首先建立图像[X]与稀疏系数集合[α=αi]之间的联系，用[xi]来表示从图像[X]的空间位置[i]处选取的图像块。得到如下公式：

[xi=RiX] （1）

这里的[Ri]表示一个矩形的窗口操作，在发生重叠的情况下，这种基于块的表示是高度冗余的。同时，[xi]复原成[X]可以用一个超定方程组来表示，同时，对于一个给定的词典[Φ]，[xi=Φαι]，从而获得如下的最小二乘解：

[X=Dα=iRTiRi-1iRTiΦαi] （2）

这里的[D]是对偶于[R]的算子，在图像去噪的背景下，得到如下的变分问题：

[α=argminα12Y-Dα22+λα1] （3）

通过观察发现，稀疏系数[α]不是随机分布的（如图1所示），他们位置的不确定性常常与图像信号的非局部自相似性相关，这意味着我们可以利用位置相关约束来增强图像信号的稀疏性。

a）一张规则纹理的图像 b）稀疏系数的空间分布

这种非线性约束是位置相关的，因此，聚类是利用这种非线性约束的一种合理方法。现存的文献中也存在大量聚类算法，例如：K-means算法、K-NN分类算法、谱聚类算法、图像分割算法。然而，数据聚类和稀疏表示是在不同层级下得出的方法（分别是高层级和低层级），为进一步了解非局部自相似性如何能够促进稀疏性，提出以下的成本函数研究：

[α，μ=argminα，μk12Y-Dα22+λ1α1+λ2k=1Ki∈CkΦαi-μk22] （4）

[μk]代表系数[α]的第[k]个簇[Ck]的质心，公式（4）表示基于聚类的正则化项，加权系数[α]是相对于[μk]的重新编码。随着进一步的压缩，利用非局部自相似性的结果，可以得到更为稀疏的表示。此前关于BM3D和LSSC的研究都是基于聚类和稀疏表示的类似算法，但是它们的关联性相对较弱。为了更好地表示新型正则化项的含义，重写公式（4），如下所示：

[α，β=argminα，μk12Y-Dα22+λ1α1+λ2k=1Ki∈CkΦαi-ΦβK22] （5）

这里[μk=Φβk]，受压缩感知算法的影响（参考文献[1]），在新型正则化项中用L1范数来替代L2范数，得到如下公式：

[α，β=argminα，μk12Y-Dα22+λ1α1+λ2k=1Ki∈Ckαi-βk1] （6）

由上述可知，CSR模型提供了一种将字典学习参数[αi]和结构聚类参数[βk]统一表示在一个变分框架下的新方法，该方法利用[αi]的结构冗余来得到更高的稀疏性。基于对[βk]的理解，它是通过结构聚类学习得到的，并且在更高层级下进行编码形成的模型。

1.2 L1最小化的迭代加权和正则化

本文的一个主要技术贡献是通过迭代算法交替更新[α]和[β]，解决了公式中的双头L1优化问题。借鉴替代函数[10]的思想，导出一个用于更新[α]和[β]的迭代收缩算子：

[α（i+1）j=ST1，T2（v（i）j）-ST1，T2（-v（i）j）βj≥0βj≤0] （7）

[V（i）=1cDT（x-Dα（i））+α（i）] （8）

其中，[Τ1=λ1c，T2=λ2c]（[c]是一个保证替代函数凸性的辅助参数），上标[i]表示迭代次数，下标[j]表示矢量中第[j]个向量的输入。结果表明，迭代收缩同样适用于分别相关于局部和非局部的两个正则参数的情况，迭代收缩在计算上的高效性使CSR模型得以完善。

与此同时，借鉴变分图像去噪[11]和加权L1优化[12]等相关文献中的思想，自适应地调整两个正则参数[T1，T2]。我们采用下述策略来更新[T1，T2]：

[T1=c1σ2wσα，T2=c2σ2wσγ] （9）

这里，[σ2w]是噪音方差，[γ=α-β]，[c1]和[c2]是两个给定的常数（通常假设[c1

受最近的相关工作[13]的启发，建议通过下式来更新恢复图像算法：

[X（i+1）=S（（1-δ）X（i）+δY）] （10）

此处[S=D?S?R]表示正则约束集合上的投影。

[（1-δ）X（i）+δY=X（i）+δ（Y-X（i））] （11）

上式是实现迭代正则思想的算子，[δ]是一个控制反馈到迭代的噪声级的的小正数。

1.3 CSR算法的贝叶斯解释

[CSR]的基本思想是，假设可以将[K]个簇的质心视作稀疏系数[α]的隐变量的对等物，其实质是[β]用于解决构成基础图像信号的不确定性问题。因此，可以制定以下最大后验估计（MAP）：

[（α，β）=argmaxα，βlogP（Yα，β）+P（α，β）] （12）

上式两项分别与可能性和先验分布相对应，第一项可以简单地通过降解模型[Y=X+W]描述，即

[P（Yα，β）=12πσwexp（-12σ2wY-Dα22）] （13）

通过独立同分布的拉普拉斯分布去建造[α]和[γ]的模型，先验模型可以通过下式给出：

[P（α，β）=i12σαexp（-αi1σα）×ki12σγexp（-α-βk1σγ）] （14）

此处[γ=α-β]定义了聚类的偏差数，把公式（13）和公式（14）代入公式（12），得

[（α，β）=argminα，βY-Dα22+22σ2wσαiαi1+22σ2wσγkiαi-βk1] （15）

设[λ1=22σ2wσα，λ2=22σ2wσγ]，它等同于前面推导出的公式（4）。

2 基于聚类的稀疏表示去噪算法

2.1算法完整描述

算法1：基于字典学习和结构聚类的图像去噪算法

初始化：[X=Y]；

外循环（字典学习）：[i=1，2，…，I]；

-通过K-means 和 PCA更新[Φ]；

内循环（结构聚类）：[j=1，2，…，J]；

-迭代正则化：[X=X+δ（Y-X）]；

-正则化参数更新：通过公式（12）获得[T1，T2]的新估计值；

-质心估计跟新：通过kNN聚类获得[βk]的新估计值；

-图像估计更新：通过[X=D?S?RX]获得[X]的新估计值；

2.2算法流程图

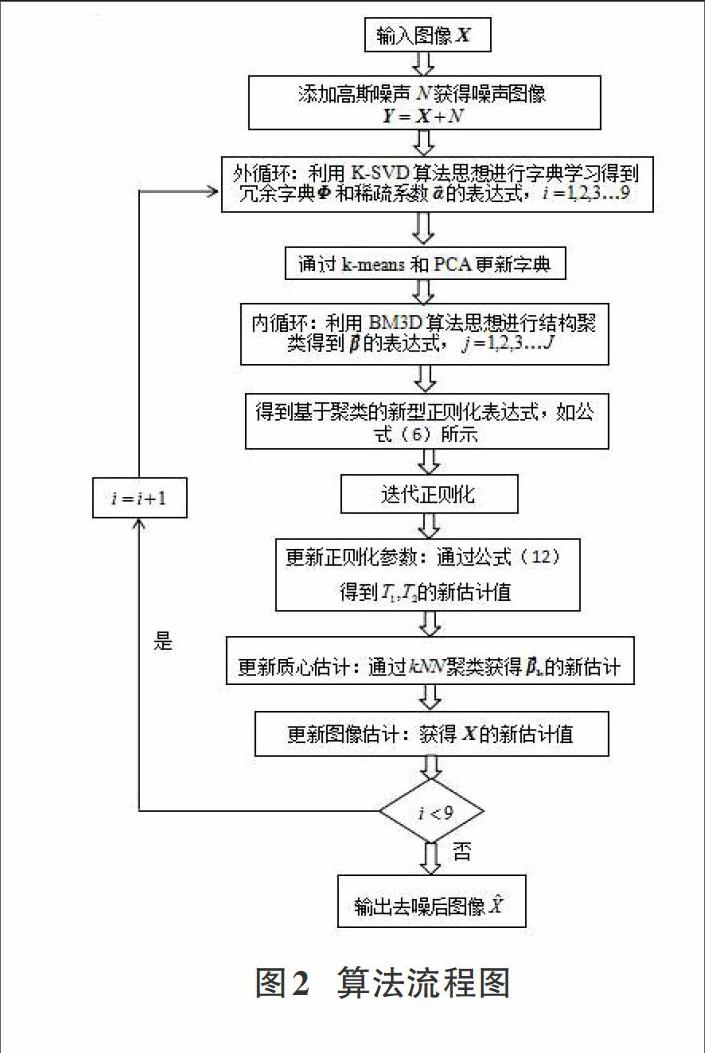
首先，输入原始图像，并对其添加高斯噪声以得到噪声图像。接着，进入外循环，利用K-SVD算法思想进行字典学习得到冗余字典[Φ]和稀疏系数[α]的表达式，并通过K-means和PCA来更新字典。随后，进入内循环，利用BM3D算法思想进行结构聚类以得到[β]的表达式，并通过迭代正则化进一步更新正则化参数，更新质心估计和图像估计值，最后，输出去噪后的图像，算法流程图如图2所示。

3 实验与分析

3.1实验初始化

我们在MATLAB上执行了CSR去噪算法，实验使用了下列参数：block-size [B]= 7， [λ] = 0.03， dictionary-size [K]= 64 ，[I]= [J]= 3。简言之，我们的CSR算法可以看成是字典学习（类似于K-SVD）和结构聚类（类似于BM3D）的复合，在CSR算法中，字典的更新是通过K-means和PCA，进行聚类的变换系数为二级稀疏编码。

3.2三种去噪算法去噪效果图像和数据的比较

对于这种规则纹理图形，CSR的表现显著优于BM3D和K-SVD。如图3所示，CSR的PSNR增益分别高出1.97分贝和0.77分贝。当图片高度自我重复时，字典学习比结构聚类起着更重要的作用，如果把它们结合在一起，就可以得到更好的效果。

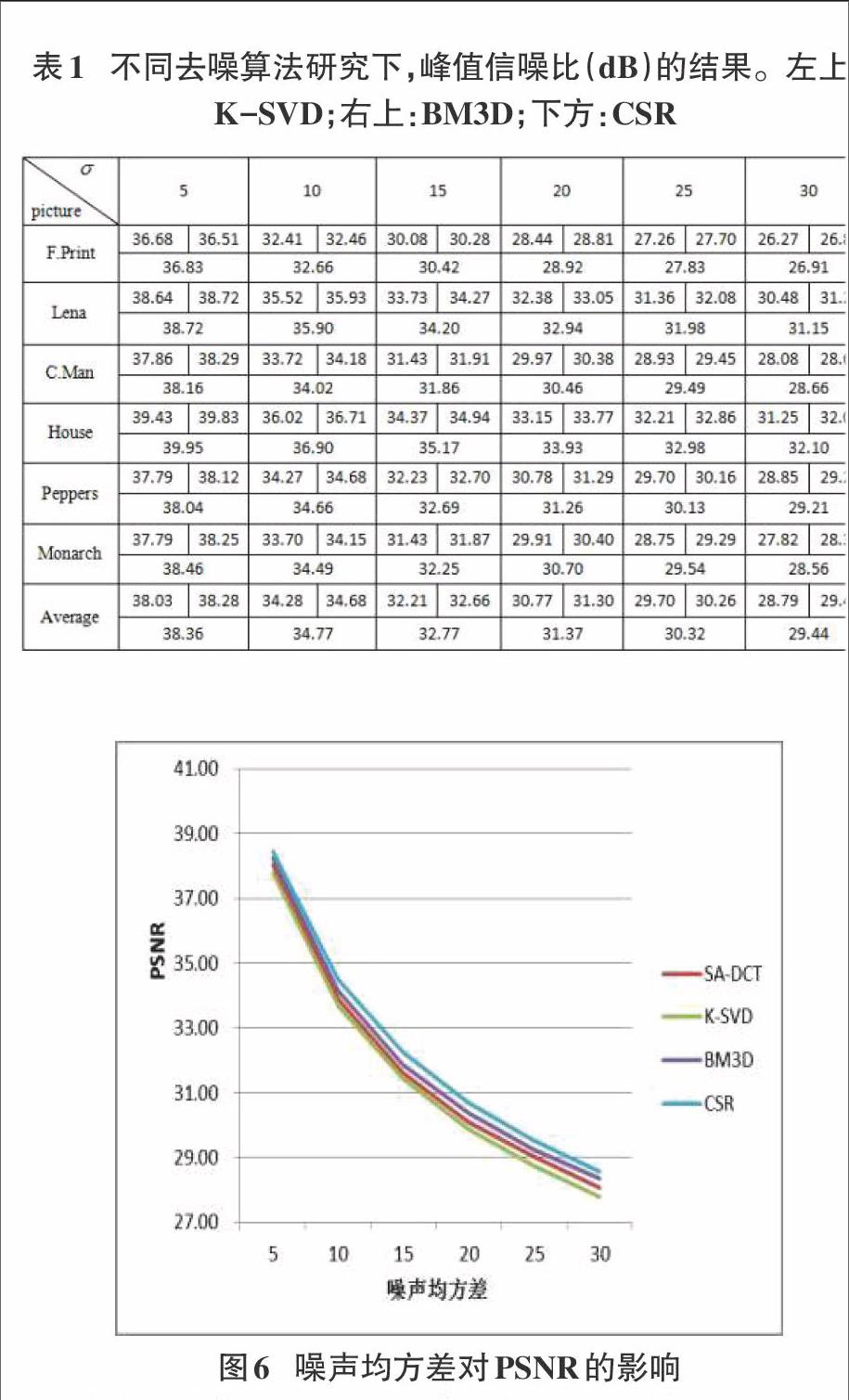
我们对12幅图像在不同的噪声级下比较了CSR和K-SVD，BM3D的去噪效果。图3～5分别为其中的2幅图像在[σw]= 20时的噪声图像。考察图中的细节，如D34中的黑色噪点，C.Man中人像周围的轮廓，House中房屋墙壁的纹理，本文算法得到的重构图像更加清晰。表1给出了其中6幅图像在更多噪声级下的PNSR比较结果。由表1可知，三种算法在图像质量的数学指标上，本文的算法是最好的。

本次实验使用Monarch图像进行测试，比较了SA-DCT，K-SVD，BM3D和CSR四种去噪算法随着噪声均方差[σ]变化时的PSNR值。从图6可以看出，随着[σ]的增大，PSNR值逐渐降低，但是[σ]越大，其对去噪效果的影响越小。我们可以更加直观地看出，与现有的流行算法（K-SVD，BM3D和SA-DCT）相比，CSR具有更高的峰值信噪比。

4 结束语

针对K-SVD算法和BM3D算法的不足，本文提出了基于字典学习和结构聚类的图像去噪算法。该算法首先通过字典学习得到含噪图像的冗余字典，然后对相似的图像块进行聚类构成块群，并通过迭代收缩和L1正则化约束，对同类的图像块在字典上进行稀疏表示，以达到降噪的目的。CSR算法体现了将全局思考与局部适配结合在一起的好处，实验结果表明，在常规的图像处理上，本文提出的算法能较好的保留图像的结构信息，峰值信噪比（PSNR）也优于现有的流行算法，具有较好的视觉效果。但是，本文提出的算法的计算量较大，需要进一步改进，与此同时，稀疏性与聚类性的微妙关系仍然需要我们进一步研究！

参考文献：

[1] E. J. Cande`s， J. K. Romberg， and T. Tao.Robust uncertainty principles： exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Infor- mation Theory， 2006，52（2）：489–509.

[2] M. Elad and M. Aharon.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans. on Image Proc.， 2006，15（12）：3736-3745.

[3] Romano Y，Elad M.Improving K-SVD denoise by post-processing its method-noise[C]//Proc of International Conference on Image Processing，2013：435-439.

[4] J. Mairal， F. Bach， J. Ponce， G. Sapiro.Online dic- tionary learning for sparse coding[J].in Proceedings of the 26th Annual International Conference on Machine Learning， 2009， ：689-696.

[5] A. Buades， B. Coll， and J.-M. Morel. A non-local algorithm for image denoising[J]. CVPR， ，2005（2）：60-65.

[6] K. Dabov， A. Foi， V. Katkovnik， K. Egiazarian.Image denoising by sparse 3-d transform-domain collaborative filtering[J].IEEE Trans. on Image Processing，2007，16（8）：2080-2095.

[7] Burger H C.Schuler C J.Harmeling.S.Image denoising：Can plain neural networks compete with BM3D[C]//Proc of International Conference of Computer Vision and Pattern Recognition，2012：2392-2399.

[8] P. Chatterjee and P. Milanfar. Clustering-based denoising with locally learned dictionaries，[J].Image Processing， IEEE Transactions on， 2009，18（7）：1438-1451.

[9] J. Mairal， F. Bach， J. Ponce， G. Sapiro， et al.Non-local sparse models for image restoration[C].in 2009 IEEE 12th International Conference on Computer Vision，2009：2272-2279.

[10] I. Daubechies， M. Defrise， and C. De Mol.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics， 2004，57（11）：1413-1457.

[11] N. Galatsanos and A. Katsaggelos.Methods for choosing the regularization parameter and estimating the noise vari- ance in image restoration and their relation[J]. IEEE Transac- tions on Image Processing， 1992，1（3）：322-336.

[12] E. Candes， M. Wakin， S. Boyd， et al.Enhancing sparsity by reweighted l1 minimization[J].Journal of Fourier Analy- sis and Applications， 2008，14（5）：877-905.

[13] S. Osher， M. Burger， D. Goldfarb， et al.An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling and Simulation， ，2005，4（2）：460–489.