摆线针轮传动接触热弹流润滑特性

孙章栋， 朱才朝， 刘怀举， 宋超省

(重庆大学 机械传动国家重点实验室,重庆　400044)



摆线针轮传动接触热弹流润滑特性

孙章栋， 朱才朝， 刘怀举， 宋超省

(重庆大学 机械传动国家重点实验室,重庆400044)

摘要：针对摆线针轮行星传动啮合过程中啮合齿面摩擦行为影响系统动态特性、传动效率及接触疲劳特性等问题，基于牛顿流体及指数率、Ree-Eyring模型建立摆线针轮线接触时变热弹流润滑数值分析模型，获得理想安装的摆线针轮副完整啮合周期内摩擦力、摩擦因数及摩擦损失功率变动。结果表明，基于牛顿流体及指数率流体模型所得摩擦因数与工程实际不符；基于Ree-Eyring模型纯滚动啮合产生的热效应在重载下对啮合过程中膜厚、摩擦损失功率影响较大，对压力、摩擦因数影响较小。研究非牛顿流体特征参数与摆线针轮传动设计参数对啮合中摩擦因数、摩擦损失功率影响规律表明，流体特征应力增加摩擦因数及损失功率均减小；短幅系数取较大值时大部分啮合区间摩擦因数增加、摩擦损失功率减小。

关键词：摆线轮；热弹流润滑；Eyring 流体；摩擦损失功率；摩擦因数

摆线针轮行星传动以传动精度高、传动比大、结构紧凑、使用周期长等优点广泛用于微型器械、机器人及测试仪器等设备。啮合过程中摩擦力及摩擦产生的热量易造成齿面磨损、胶合等失效形式，不仅影响齿轮的传递精度及接触疲劳[1-3]，且会影响传动系统动态特性及传动效率[4]。 Dyson等[5-6]通过弹流润滑数值计算求得啮合中摩擦力及损失效率。 Goksem等[7]利用弹流润滑数值分析推导出光滑等温线接触摩擦力公式。 Jacod等[8]利用 Ree-Eyring流体拟合出光滑等温点接触弹流润滑摩擦因数公式。 Chang等[9]基于光滑接触表面，通过简化能量、压力及膜厚方程计算渐开线齿轮摩擦功率损失。Wu等[10]利用Ree-Eyring流体建立混合弹流润滑数值模型，并求得渐开线齿轮啮合的摩擦功率损失。 Li等[11-12]在文献[10]基础上建立渐开线时变混合弹流润滑数值模型，表明滚动引起的摩擦功率损失占总摩擦功率损失30%以上，并利用线性回归方法拟合出摩擦因数、损失功率公式。

以上研究均针对渐开线齿轮润滑问题，对摆线针轮弹流润滑特性研究较少。而两者传动存在明显区别，即摆线轮与针轮同时啮合齿数多于渐开线齿轮，理论上可达一半摆线轮；摆线轮与针轮啮合理论上为纯滚动线接触，渐开线齿轮啮合相位在节点处为纯滚动线接触，其它啮合相位为滑动线接触。本文基于牛顿流体、指数率流体及Ree-Eyring流体建立摆线针轮光滑接触的时变热弹流润滑数值模型，研究摆线针轮纯滚动啮合中摩擦因数、损失功率变化规律。

1几何与运动学分析

表1 摆线针轮传动副及润滑相关参数

图1　摆线轮与针齿啮合示意图Fig.1 Diagram of the meshing between the cycloid gear and the rollers

啮合中摆线轮曲率半径ρ变化，针齿半径rz为定值，得当量曲率半径及载荷[13]分别为

R=ρrz/(ρ±rz)

(1)

(2)

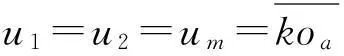
(3)

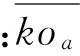
等效曲率半径、卷吸速度、单位啮合力随啮合相位变化曲线见图2。由图2看出，标准齿廓单位啮合力F、等效曲率半径R及卷吸速度ur经θ=arccosK1时趋势发生突变，故应考虑Reynolds方程的时变项对润滑特性影响。

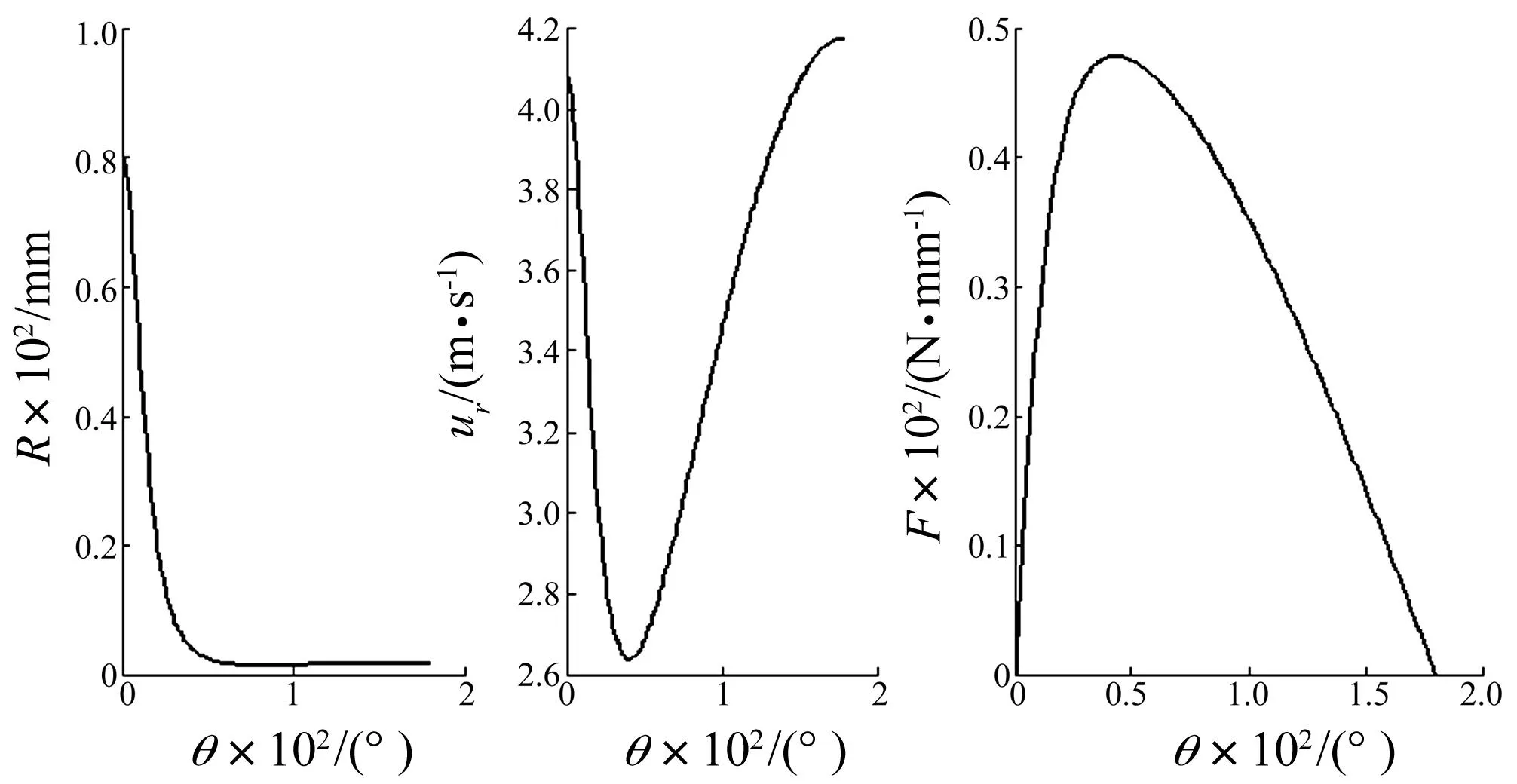
图2　等效曲率半径、卷吸速度、单位啮合力随啮合相位变化Fig.2 The variation of equivalent radius, rolling speed and contact force with meshing process

2摆线针轮时变热弹流润滑模型

由润滑力学观点，将摆线轮轮齿与针轮接触简化为一当量半圆柱与一平面接触，使其构成的间隙形状相同，见图3。

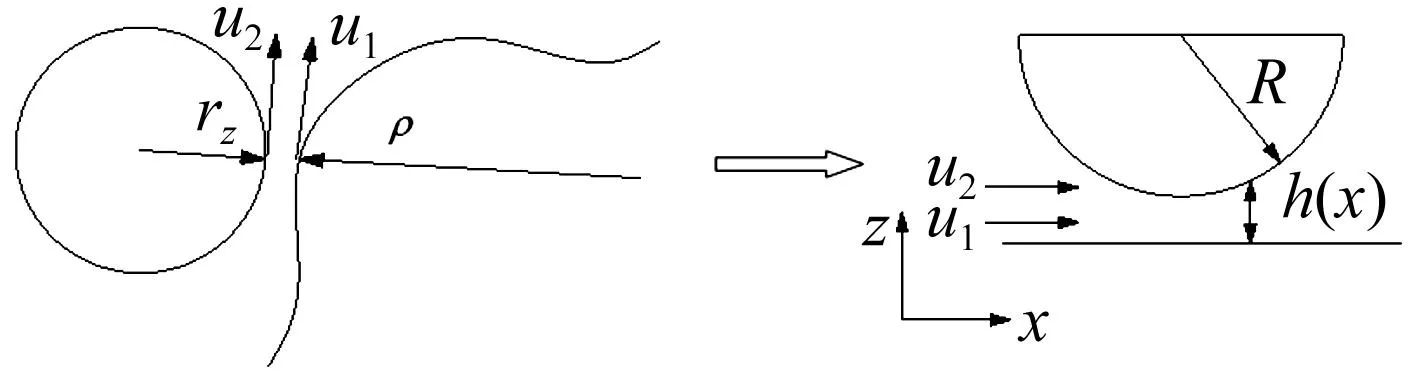
图3　简化的线接触模型Fig.3 Simplification of a line contact problem

不同润滑油会呈现不同的流变特性，三种流体本构方程[14]如下：

(1)牛顿流体本构方程

(4)

式中：η为黏度函数。

若用Roelands方程，则黏度方程为

(5)

式中：z0=α/[5.1×10-9g(lnη0+9.67)]，η0为环境黏度；s=β(T0-138)/(lnη0+9.67)，T0为环境温度；α为黏压系数；β为黏温系数。

(2)Ostwald-de Waele流体本构方程

(6)

式中：n为流变指数；m为关于压力、温度黏性函数，即

(7)

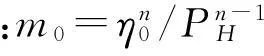
(3) Ree-Eyring流体本构方程

(8)

式中：τ0为流体特征剪应力。

用广义Reynolds方程，引入等效黏度η*，将非牛顿流体转成牛顿流体求解。三种流体对应的等效黏度计算式为

利用Hertz接触参数对润滑模型无量纲化，各参考量为

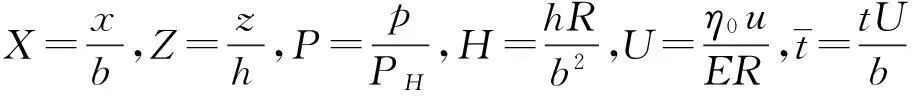
式中：x为流动方向；z为膜厚方向；b为Hertz接触半宽，h为油膜厚度；p为油膜压力；PH为最大Hertz压力；R为等效曲率半径；E为等效弹性模量；t为时间；T为温度。

无量纲Reynolds方程为

(9)

油膜无量纲能量方程为

(10)

固体无量纲能量方程为

(11)

无量纲化膜厚方程、Dowson-Higginson密度方程、载荷方程，无量纲Reynolds方程、油膜无量纲能量方程及固体无量纲能量方程边界条件见文献[15-16]。离散无量纲Reynolds方程形式[17]为

αipi-1+βipi+γipi+1=δi

(12)

式中：αi，βi，γi，δi为Poiseuille流、Couette流及Squeeze流差分系数和。

离散成该形式可方便压力迭代中利用追赶法求解压力。本文用二阶中心差分离散Poiseuille流、一阶向后差分离散格式Couette流及一阶向后差分离散格式Squeeze流。

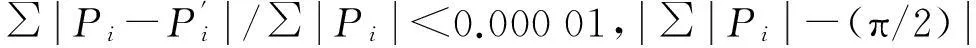
弹流润滑分析中计算接触副摩擦因数采用两接触线的剪切力均值与载荷比值，即

(13)

计算接触副摩擦功率损失为该接触点沿膜厚方向剪力与膜厚层间滑动速度乘积并沿膜厚积分，即

(14)

式(14)进一步化简为

Pr(X)=

(15)

纯滚动时U2-U1=0，故式(15)中第二项可略去，摩擦损失功率大小主要取决于dP/dX，光滑接触副Hertz接触区域dP/dX变化小，该区域摩擦损失功率亦小，而入、出口接触区域dP/dX变化大，该区域摩擦损失功率亦大。整个接触区域滚动摩擦损失功率损失为

(16)

3结果与讨论

标准齿廓单位啮合力、等效曲率半径及卷吸速度变化曲线拐点均发生于相位角θ=arccosK1处。标准齿廓三种流体在该相位处的压力、膜厚、剪切力及摩擦损失功率变化曲线见图4～图6。

图4　θ=arccos K1处牛顿流体压力、膜厚、剪力及滚动摩擦损失功率曲线Fig.4 Thecurves of the pressure, film thickness, shear stress and rolling power lossat the phase θ=arccos K1 with the newtonian fluid

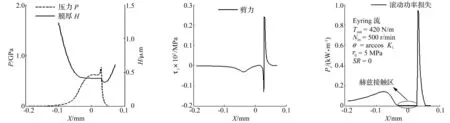
图5　θ=arccos K1处Ree-Eyring流体压力、膜厚、剪力及滚动摩擦损失功率曲线Fig.5 Thecurves of the pressure, film thickness, shear stress and rolling power lossat the phase θ=arccos K1 with an Eyring fluid

由3图看出，纯滚动条件下，三种流体热弹流解的压力、膜厚仍具有等温弹流润滑特征。滑动下的接触面剪力分布与所得压力分布相似，而纯滚下的Hertz接触区域值较小，二次压力峰对应位置存在正负峰值，且与膜厚颈缩有关。牛顿流体计算的剪力较Ree-Eyring流体大，摩擦因数也会偏大。Ostwald (指数率)流体所得剪力远大于前两种流体且为正值，与工程实际不符。三种流体所得摩擦损失功率共同点为：在Hertz接触区域接近零，在接触入、出口区域较大，与摩擦损失功率公式分析结果一致。而指数率流体摩擦损失功率较大，与工程实际不符。Ree-Eyring流体及牛顿流体所得值符合工程实际，前者常用于热弹流解可获得合理摩擦因数[18]，利用该模型所得剪力及滚动摩擦损失功率大小与文献[12]一致，Ostwald-de Waele及牛顿流体模型虽可求得合理的膜厚、压力曲线，但剪力、滚动摩擦损失功率与工程实际不符。本文用Ree-Eyring流体模型研究摆线针轮接触润滑特性。

图6　相位角θ=arccos K1处指数率流体压力、膜厚、剪力及滚动摩擦损失功率曲线Fig.6 Thecurves of the pressure, film thickness, shear stress and rolling power lossat the phase θ=arccos K1 with an Ostwald fluid

利用牛顿流体所得摆线针轮纯滚动啮合中最小膜厚稳态及瞬态数值解，并与Dowson-Higginson润滑油膜厚经验公式[19]比较，见图7。由图7看出，数值解与经验公式解变化趋势基本吻合，经验公式值偏大，因此可验证数值模型的正确性及数值分析的必要性。而最小膜厚瞬态数值解与稳态数值解存在差别，随啮合相位增加瞬态数值解先大于稳态数值解，在某一瞬啮合相位处与稳态解结果相等，啮合相位结束阶段小于稳态解，表明Reynolds方程中需考虑时变项对摆线针轮啮合的润滑状态影响。

图7　最小膜厚数值解与Dowson-Higginson经验公式比较Fig.7 Compare film thickness numerical solution with the empirical Dowson-Higginson formula

3.1纯滚动时热效应对润滑特性影响

Ree-Eyring流体高速重载下摆线针轮纯滚动啮合中热解及等温解的中心压力、最小膜厚、摩擦因数及摩擦损失功率变化曲线见图8，可见啮合的中心压力与摩擦因数基本无差别，热解所得最小膜厚较等温解小，滚动摩擦损失功率热解与等温解存在较大差别。表明重载下纯滚动产生的热效应对润滑特性影响不可忽略。

3.2流体特征对润滑特性影响

摆线针轮啮合的中心压力、最小膜厚、摩擦因数及摩擦损失功率随Ree-Eyring流体特征应力τ0变化曲线见图9、图10。由2图看出，随特征应力增加整个啮合过程中心压力略有减小，最小膜厚略增加；特征应力进一步增加时中心压力及最小膜厚变化幅度减小，整个啮合过程的摩擦因数减小，滚动摩擦损失功率也减小。

3.3短幅系数k1对润滑特性影响

摆线针轮啮合过程中心压力、最小膜厚、摩擦因数及滚动摩擦损失功率随短幅系数k1变化曲线见图11、图12。由2图看出，摆线针轮传动设计允许范围内，随短幅系数增加啮合中最大中心压力变增大，整个啮合区间内最小膜厚减小，大部分啮合区间内摩擦因数增加，而整个啮合区间滚动摩擦损失功率减小。

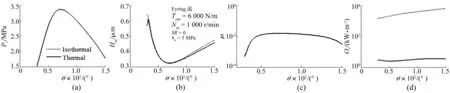
图8　高速重载下纯滚动产生热效应对压力、膜厚、剪力及滚动摩擦损失功率影响Fig.8 Influence of the thermal effect produced by pure rolling on the pressure, film thickness, friction coefficient and rolling power loss at high load and speed

图9　啮合过程中心压力及最小膜厚随特征应力变化Fig.9 Influence of the Eyring stress on the center pressure and minimum film thickness

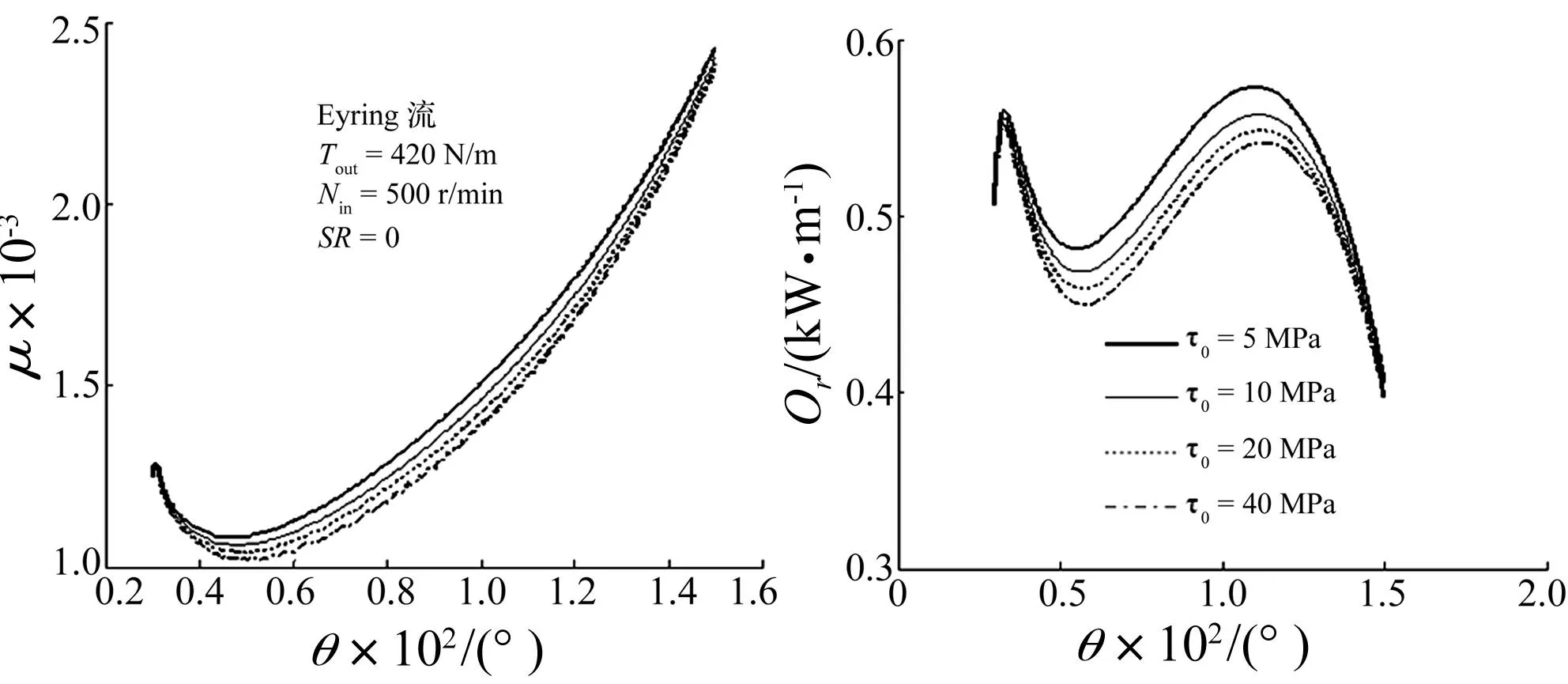
图10　啮合过程摩擦因数及滚动损失功率随特征应力变化Fig.10 Influence of the Eyring stress on the friction coefficient and rolling power loss

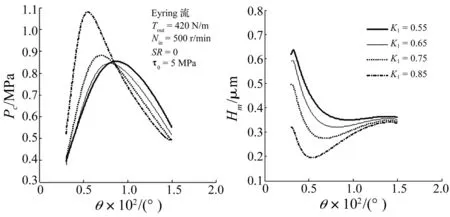
图11　啮合过程中心压力及最小膜厚随短幅系数K1变化Fig.11 Influence of short width coefficient on the center pressure and minimum film thickness

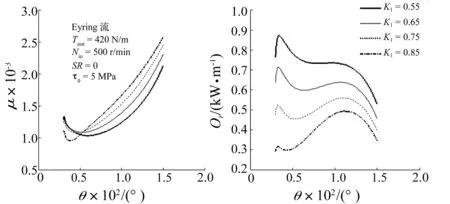
图12　啮合过程剪力及滚动损失功率随幅系数K1变化Fig.12 Influence of Short width coefficient on the friction coefficient and rolling power loss

4结论

采用广义Reynolds方程，求得Newton、指数率及Ree-Eyring流体等效黏度，建立摆线针轮线接触时变热弹流润滑数值模型，计算完整啮合周期内不同润滑流体类型的摩擦因数及损失功率变动。用追赶法求解压力及温度场，用DC-FFT算法[20]快速求解弹性变形，结论如下：

(1)基于牛顿及指数率流体模型可获得合理的膜厚、接触压力曲线，剪力及摩擦损失功率与工程实际不符。

(2)基于Ree-Eyring模型纯滚动啮合的热效应重载下对啮合中膜厚及滚动摩擦损失功率影响较大，对接触压力及摩擦因数影响较小。

(3)特征应力增加膜厚增加，摩擦因数及滚动摩擦损失功率均减小；在摆线轮设计允许范围内短幅系数取较大值时最小膜厚减小，大部分啮合区间内摩擦因数增加，整个啮合区间滚动摩擦损失功率减小。

参 考 文 献

[1] Zhu D, Martini A, Wang W, et al. Simulation of sliding wear in mixed lubrication[J]. Journal of Tribology, 2007,129(3): 544-552.

[2] Liu H, Mao K, Zhu C, et al. Mixed lubricated line contact analysis for spur gears using a deterministic model[J]. Journal of Tribology, 2012, 134:021501-021507.

[3] Liu H, Mao K, Zhu C,et al. Spur gear lubrication analysis with dynamic loads[J]. Tribology Transactions, 2013,56(1): 41-48.

[4] 朱才朝,陈爽,马飞,等. 轮齿修形对兆瓦级风电齿轮箱动态特性影响[J]. 振动与冲击,2013,32(7):123-128.

ZHU Cai-chao, CHEN Shuang, MA Fei,et al. Effect of gear teeth modification on dynamic characteristics of a megawatt level wind turbine gearbox[J].Journal of Vibration and Shock,2013,32(7):123-128.

[5] Dyson A. Frictional traction and lubricant rheology in elastohydrodynamic lubrication[J]. Philosophical Transactions of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1970, 266: 1-33.

[6] Dama R, Chang L. An efficient and accurate calculation of traction in elastohydrodynamic contacts[J]. Wear, 1997, 206: 113-121.

[7] Goksem P G, Hargreaves R A. The effect of viscous shear heating on both film thickness and rolling traction in an EHL line contact[J]. Journal of Lubrication Technology, 1978,100: 346-352.

[8] Jacod B, Venner C H, Lugt P M. A generalized traction curve for EHL contacts[J]. Journal of Tribology, 2000,123(2):248-253.

[9] Chang L, Jeng Y R,Huang P Y. Modeling and analysis of the meshing losses of involute spur gears in high-speed and high-load conditions[J]. Journal of Tribology, 2012, 135(1): 011504-011504.

[10] Wu S, Cheng H S. A friction model of partial-EHL contacts and its application to power loss in spur gears[J]. Tribology Transactions, 1991,34(3):398-407.

[11] Li S,Kahraman A. Prediction of spur gear mechanical power losses using a transient elastohydrodynamic lubrication model[J]. Tribology Transactions, 2010,53(4): 554-563.

[12] Li S, Kahraman A. A method to derive friction and rolling power loss formulae for mixed elastohydrodynamic lubrication[J]. Journal of Advanced Mechanical Design Systems and Manufacturing, 2011, 5 (4): 252-263.

[13] 孙章栋,朱才朝,刘怀举,等.摆线针轮传动线接触弹流润滑分析[J].振动与冲击,2014,33(23):195-199.

SUN Zhang-dong, ZHU Cai-chao, LIU Huai-ju, et al. Numerical analysis of elastohydrodynamic lubrication for cycloid drives[J]. Journal of Vibration and Shock,2014,33(23):195-199.

[14] Liu Ming-yong, Zhu Cai-chao, Liu Huai-ju,et al. Effects of working conditions on TEHL performance of a helical gear pair with non-newtonian fluids[J]. Journal of Tribology, 2014,136(2): 021502-021510.

[15] Yang Pei-ren,Wen Shi-zhu. A generalized Reynolds equation for non-newtonian thermal elastohydrodynamic lubrication [J]. Journal of Tribology, 1990,112(4): 631-636.

[16] Venner C H. Multigrid solution of the EHL line and point contact problems[D]. Enschede：University of Twente, 1991.

[17] Liu Y C, Wang Q J, Wang W Z,et al. Effects of differential scheme and mesh density on EHL film thickness in point contacts[J]. Journal of Tribology-Transactions of the Asme, 2006,128(3): 641-653.

[18] Liu X, Jiang M, Yang P, et al. Non-newtonian thermal analyses of point EHL contacts using the Eyring model[J]. Journal of Tribology, 2005, 127(1): 70-81.

[19] Dowson D. Elastohydrodynamics[M]. London: Imperial College Press, 1968:182.

[20] Wang W, Wang H, Liu Y,et al. A comparative study of the methods for calculation of surface elastic deformation [J].Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2003, 217(2): 145-154.

TEHL characteristics of a cycloid drive

SUNZhang-dong,ZHUCai-chao,LIUHuai-ju,SONGChao-sheng

(The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China)

Abstract:A cycloid drive belongs to precision drives and its meshing friction influences the dynamic characteristics of the system, the transmission efficiency, and the contact fatigue. A time-varying thermal elastohydrodynamic lubrication line contact model was developed for the cycloid drives with Newtonian fluid, Ree-Eyring fluid, or Ostwald-de Waele fluid in order to investigate rolling contact friction, friction coefficient, and frictional power loss in the meshing period. Studies show that shear stress and rolling power loss calculated with Ostwald-de Waele fluid and Newton fluid do not agree with the engineering practice. The thermal effect produced by pure rolling with Ree-Eyring fluid affects the film thickness and the frictional power loss, and its influence on the pressure and friction coefficient is small. At the end of the paper, the effect of Ree-Eyring stress and design parameters on the friction coefficient and rolling power loss are discussed. As the Eyring stress increases, the friction coefficient and rolling power loss decreases; As the short width coefficient goes up, the friction coefficient at most engaging moments increases and rolling power loss decreases.

Key words:cycloid drive; TEHL; Eyring fluids; frictional power loss;friction coefficient

中图分类号:TH117

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.032

通信作者朱才朝 男，教授，博士生导师，1966年生

收稿日期：2014-10-08修改稿收到日期：2015-03-20

基金项目：国家自然科学基金(51175523;51405042;51405043)；国家科技支撑计划(2012BAA01B05)

第一作者 孙章栋 男，博士生，1984年11月生

E-mail：cczhu@cqu.edu.cn