基于等效转化关系的一维非均匀介质波动问题解析方法研究

杨在林， 王　耀， 黑宝平， 李志东

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨　150001)



基于等效转化关系的一维非均匀介质波动问题解析方法研究

杨在林， 王耀， 黑宝平， 李志东

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨150001)

摘要：基于波动方程与位移场解答等效思路，获得非均匀介质波动问题与均匀介质柱面波等效转化关系。分析发现两类问题模型间可相互转化，问题解答可相互等效。等效转化实质为几何形状与材料参数的等效关系。利用等效转化关系获得两个一维非均匀介质波动问题算例的解析解。

关键词：非均匀介质；波动；等效转化

生产实践中均匀介质的柱面波较常见，一般由直线源引起，如受时变均布内压作用的直孔结构[1]。对常见的标量波如线性浅水波[2]在一定条件下也可视为类似情形。均匀线弹性介质中波速是恒定的，即单位时间内波传播距离不变。均匀介质中传播的平面波波速、波幅均为恒定的，而柱面波波幅则随传播距离增加逐渐递减。非均匀介质则有所不同[3-4]。由于材料参数分布不均匀，传播过程中波幅一般随时间变化，且波速也会随波的位置不同而不断变化。

Virieux[5-6]采用速度-应力有限差分法分别模拟、研究SH波、P波及SV波在非均匀介质中的传播规律；Wesoloski[7]研究两弹性层间夹有弹性模量服从二次多项式分布的过渡层的波传播规律，过渡层模量分布是以坐标为变量的抛物线，在研究域内模量分布函数完全连续；Manolis[8]研究波速竖向渐变的非均匀半无限空间中波动问题，并引入材料参数的随机性用Green函数法进行分析；Chaix等[9]通过均匀化方法对混凝土中热损伤的超声特性进行理论分析，并实验验证。

非均匀介质波动问题解析求解存在较大困难，多采用数值求解方法[10-13]。由于目前缺乏问题的解析解，数值解法结果验证较困难。

本文给出波速恒定(模量与密度非均匀)而波幅在传播过程中会发生改变、且波幅变化规律与柱面波相同的一维非均匀介质等效模型及材料参数等效转化关系,并利用此关系直接获得非均匀介质波动问题的解析解。

1方程等效

本文核心思想为利用问题模型等效转化关系求解非均匀介质波动问题的解析解。为此，建立均匀介质中柱面波问题与非均匀介质中平面波问题之间等效转化关系，建立波动方程。

1.1柱面波波动方程

各向同性均匀介质的无阻尼波动方程为

(1)

式中：D为介质弹性系数；ρ为介质密度。

柱坐标系下式(1)可表示为通式，即

(2)

1.2变截面杆波动方程

一维变截面匀质杆件波动方程为

(3)

式中：A为与坐标相关的杆截面积函数；c为杆中弹性波传播速度。

单位高度圆柱形波阵面面积A关于波阵面半径r的变化关系为

A=2πr

(4)

将式(3)中变量x用r代替，并将式(4)代入该式，有

(5)

整理得

(6)

杆中波速公式为

(7)

式中：D为拉压弹性模量(P波时)或剪切弹性模量(S波时)。

式(6)为式(2)的另一种形式。由此可知，一维变截面均质杆件波动方程与柱面波问题波动方程完全等效。

1.3向一维非均匀介质转化

一维非均匀介质波动方程为

(8)

令

D′=x

(9)

(10)

得

(11)

将式(11)中变量x用r代替，可知材料参数分布满足式(9)、(10)形式的一维非均匀介质与一维变截面均质杆件等效，即与均匀介质中柱面波式(2)等效。或视为半无限非均匀介质中平面波问题与均匀介质中柱面波问题的等效。

2等效解答

由式(7)可知，式(9)、(10)对应的非均匀介质波速为cb，与等效均匀介质中柱面波速对应且相同。可见，均匀介质中柱面波问题向非均匀介质波动问题的转化在等波速剖面条件下进行，故两者解答也可直接相互移植。因此，以SH波为例进行说明。

2.1非均匀介质等效刚度

令长度为L的一维非均匀介质沿长度方向剪切弹性模量满足关系

G′=αx

(12)

式中：α为待定系数。

则在单位截面积下该介质轴向等效柔度系数为

(13)

即轴向等效刚度系数为

(14)

2.2均匀介质等效刚度

令半径为L的均匀介质剪切弹性模量为

G=μ

(15)

该介质径向等效柔度系数为

(16)

径向等效刚度系数为

(17)

2.3点源SH波位移场

设波源是简谐的，则柱面波波动方程可写为

(18)

点源SH波位移场[14]为

(19)

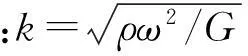
2.4非均匀介质中平面波位移场

基于本文等效方法思路，对等效非均匀介质中对应问题，其位移场的解应满足

(20)

式中：λ为待定比例系数。

由KI=KH，即

(21)

得

α=2πμ

(22)

有

(23)

将式(12)、(23)代入式(20)，得位移场的解为

(24)

3算例

本文等效关系能用于一维非均匀介质波动问题解析解。

3.1算例1

一维半无限长非均匀直杆，在O端入射频率为ω的谐波，设波在研究域外传播时不产生回波。见图1。

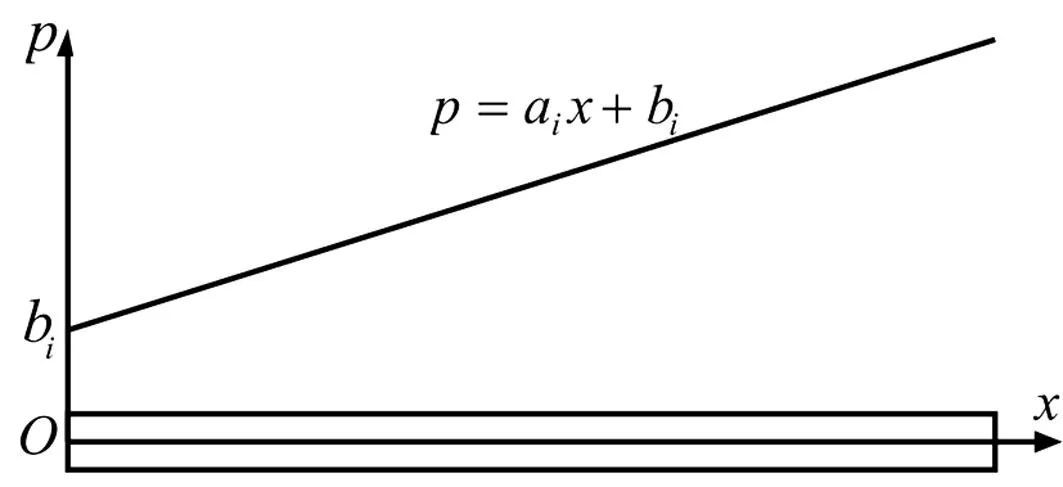
图1　模型Fig.1 Model

研究域内杆的弹性模量与质量密度均呈线性变化，分布函数分别为

E(x)=a1x+b1

(25)

ρ(x)=a2x+b2

(26)

且满足关系

a1b2=a2b1

(27)

(1)ai=0、bi>0时，杆为均匀介质，可直接给出位移场，即

(28)

(2)ai>0、bi≥0时，用坐标变换关系为

(29)

则材料参数的分布函数变为

E(x′)=a1x′

(30)

ρ(x′)=a2x′

(31)

在此情形下，问题模型与均匀介质中柱面波问题等效，等效模型弹性模量为a1/(2π)，密度为a2/(2π)。见图2。

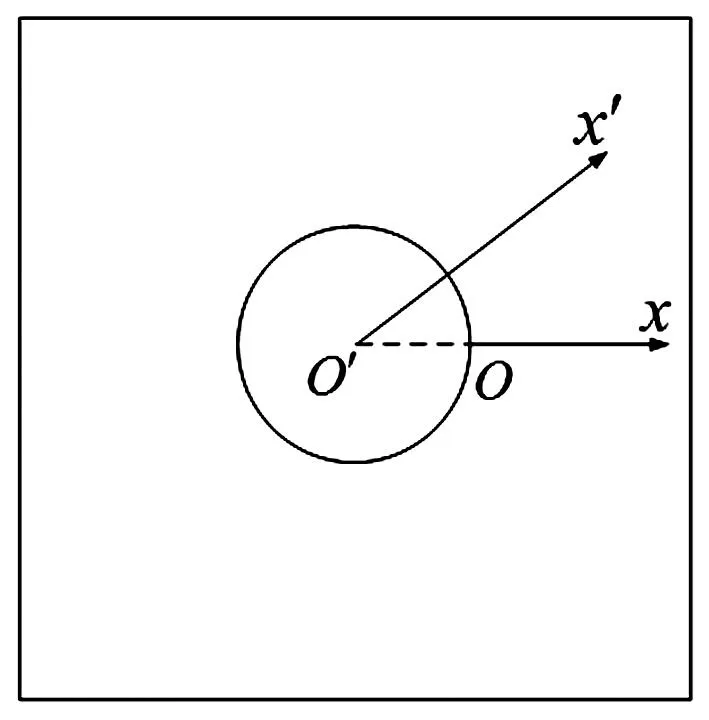
图2　等效模型(ai>0,bi≥0)Fig.2 Equivalent model when ai>0,bi≥0

据式(19)或式(24)得位移场结果为

(32)

(3)ai<0、bi>0时，用坐标变换关系为

(33)

则材料参数的分布函数变为

E(x′)=-a1x′

(34)

ρ(x′)=-a2x′

(35)

等效模型见图3，其弹性模量为-a1/(2π)，密度为-a2/(2π)。

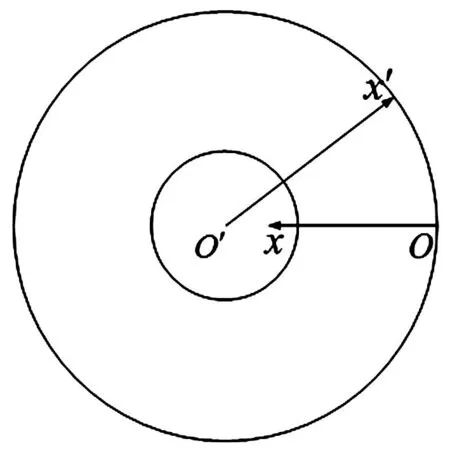
图3　等效模型(ai<0，bi>0)Fig.3 Equivalent model when ai<0，bi>0

位移场结果为

(36)

3.2算例2

一维无限长非均匀介质由材料参数不同的4段组成，见图4。其中，第1、4段分别向无限远处延伸，且材料均匀，两者性状相同；第2段长L，材料非均匀，弹性模量与质量密度的分布函数分别满足式(25)～式(27)；第3段长L，材料非均匀，弹性模量与质量密度的分布函数沿x轴方向线性递减。

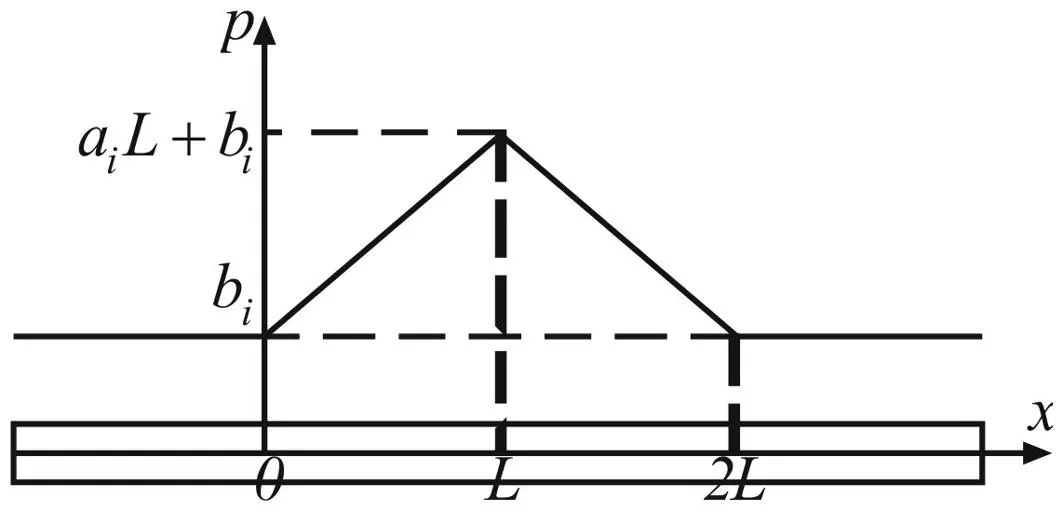
图4　模型Fig.4 Model

由x=-∞传来频率为ω的高频谐波，设在x=0处观测到

u(0,t)=e-i(ωt+φ0)

(37)

则左段(x≤0)位移场为

(38)

参考算例1结果(式(28)、(32)、(36))知

(1)ai=0时第2～4段(x>0)位移场结果为

(39)

(2)当ai>0时第2段(0

(40)

则x=L处位移为

(41)

故第3段(L

(42)

则x=2L处的位移为

(43)

故第4段(x>2L)的位移场结果为

(44)

(3)当ai<0时第2段(0

(45)

取x=L处位移uL=u(L,t)，则第3段(L

(46)

取x=2L处位移u2L=u(2L,t)，则第4段(x>2L)的位移场结果为

(47)

4结论

基于方程与解答的等效方法给出均匀介质中柱面波问题与一维非均匀介质波动问题间等效转化关系；利用该关系获得材料参数及弹性模量服从线性分布的一维非均匀介质波动问题的算例解析解，结论如下：

(1)二维柱面波问题解答可与对应的一维波动问题解答相互等效。所得转化关系本质是几何形状与材料参数间的等效关系。

(2)所得解析解为数值解法研究提供可供对比的精确结果；所得等效转化关系显示几种不同类型问题间内在联系。本文结果对非均匀介质波动问题的研究具有积极意义。

参 考 文 献

[1] Wang Li-li. Foundations of stress waves[M]. Amsterdam:Elsevier Science Ltd, 2006.

[2] Mutlubas N D. Local well-posedness and wave breaking results for periodic solutions of a shallow water equation for waves of moderate amplitude[J]. Nonlinear Analysis: Theory, Methods & Applications, 2014, 97: 145-154.

[3] Weng C C. Waves and fields in Inhomogeneous media[M]. New York: Van Nostrand Reinhold, 1990.

[4] Nolen J, Ryzhik L. Traveling waves in a one-dimensional heterogeneous medium[J]. Annales de l’Institut Henri Poincare (C) Non Linear Analysis,2009,26(3):1021-1047.

[5] Virieux J. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1957.

[6] Virieux J. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901.

[7] Wesolowski Z. Wave reflection on a continuous transition zone between two homogeneous materials[J].Acta Mechanica,1994, 105: 119-131.

[8] Manolis G D. Harmonic elastic waves in continuously heterogeneous random layers[J]. Engineering Analysis with Boundary Elements, 1997,19:181-198.

[9] Chaix J F, Garnier V, Corneloup G. Ultrasonic wave propagation in heterogeneous solid media: theoretical analysis and experimental validation[J]. Ultrasonics,2006,44:200-210.

[10] JafarGandomi A, Takenaka H. FDTD3C-A FORTRAN program to model multi-component seismic waves for vertically heterogeneous attenuative media[J]. Computers & Geosciences, 2013,51: 314-323.

[11] Benito J J, Ureab F, Gavete L,et al. A GFDM with PML for seismic wave equations in heterogeneous media[J]. Journal of Computational and Applied Mathematics,2013,252(252):40-51.

[12] Yang Zai-lin, Wang Yao, Hei Bao-ping. Transient analysis of 1D inhomogeneous media by dynamic inhomogeneous finite element method [J]. Earthquake Engineering and Engineering Vibration, 2013, 12(4)：569-576.

[13] 王耀,杨在林,黑宝平. 不同加载速率下一维非均匀介质位移响应研究[J]. 东北大学学报, 2013, 34(增刊2): 18-21.

WANG Yao, YANG Zai-lin, HEI Bao-ping. An investigation on the displacement response in one-dimension inhomogeneous media under different loading speeds [J]. Journal of Northeastern University, 2013, 34(Sup2): 18-21.

[14] Hsing P Y. Elastic waves in solids[J]. Journal of Applied Mechanics, 1983,50(4):1152-1164.

Analytical solutions to wave motion in a one-dimensional inhomogeneous medium based on an equivalent transformation relationship

YANGZai-lin,WANGYao,HEIBao-ping,LIZhi-dong

(College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract:Based on the idea of the equivalent wave motion equation and the equivalent displacement field solution, the equivalent transformation relationship was obtained between the wave in the 1D inhomogeneous medium and the cylindrical wave in the homogeneous medium. Each model can be transformed equivalently into the other. The solutions of these two problems are equivalent to each other. The nature of the equivalent transformation is the equivalent relationship between geometry and material parameters. According to the relationship, analytic solutions were obtained for two examples of the wave motion problems in the 1D inhomogeneous medium in this work.

Key words:inhomogeneous medium; wave motion; equivalent transformation

中图分类号:O343.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.028

收稿日期：2014-09-09修改稿收到日期：2015-03-25

基金项目：国家科技支撑计划课题(2015BAK17B06)；2015年地震行业科研专项经费项目(201508026-02)；黑龙江省自然科学基金(A201310)；黑龙江省博士后科研启动金(LBH-Q13040)；中央高校基本科研业务费专项资金资助项目(HEUCF150203)

第一作者 杨在林 男，博士，教授，1971年5月生