基于近似模型管理的汽车安全带约束系统优化设计

刘　鑫， 吴　钢， 尹来荣

(1.长沙理工大学 道路灾变防治及交通安全教育部工程研究中心，长沙　410004；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙　410082)



基于近似模型管理的汽车安全带约束系统优化设计

刘鑫1,2， 吴钢1， 尹来荣1

(1.长沙理工大学 道路灾变防治及交通安全教育部工程研究中心，长沙410004；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082)

摘要：为提高汽车安全带约束系统的安全防护能力，通过实车碰撞实验对安全带约束系统数值模型进行校正；基于径向基函数建立安全带约束系统的近似模型，运用IP-GA遗传算法对安全带约束系统的动态特性参数进行优化。优化中为控制由近似模型所致误差，通过模型管理更新近似模型，并将误差达到允许范围内优化解作为实际问题的解。结果表明，该方法能快速有效获得安全带约束系统的最佳匹配参数,确保汽车乘员的安全性。

关键词：安全带约束系统；近似模型管理；优化设计

汽车安全已成为制约交通运输及汽车工业发展的重要因素，进行汽车安全性研究十分必要[1-2]。车辆发生碰撞时安全带约束系统能有效避免或降低二次碰撞对乘员的损伤[3]。实践表明[4]，良好的安全带约束系统可大幅度减少乘员损伤、降低死亡率。安全带约束系统是汽车安全技术研究的重中之重[5-6]。

汽车安全带约束系统作为乘员有效的防护装置，对其安全性研究均通过诸多实车碰撞试验验证，人力、物力投入巨大，且设计结果不理想，不能成为使用的唯一手段。对此，本文采用理论与实验相结合方法，基于MADYMO分析软件建立某型汽车前碰撞安全带约束系统数值模型，并通过实车前碰撞实验进行校正；考虑数值模型的复杂性，利用径向基函数(Radial Basis Function,RBF)建立安全带约束系统近似模型；运用IP-GA遗传算法该系统动态特性参数进行优化；通过模型管理更新近似模型，控制迭代过程中由近似模型所致误差；将误差达到允许范围的优化解作为实际问题解，确保乘员的安全性。

1安全带约束系统数值模型建立

基于MADYMO分析软件建立某微型客车100%正面碰撞安全带约束系统数值模型，见图1。该模型主要由车体、假人及安全带组成。其中车体模型主要包括座椅、地板、脚踏板、前围板，转向系统、前挡风玻璃及A柱；假人模型采用HybridⅢ50百分位多刚体男性假人；为准确模拟安全带与假人身体接触、安全带在滑环两侧滑动及在卷收器拉入拉出，用二维膜单元有限元安全带模型及一维多刚体安全带模型即混合三点式安全带模型。

图1　安全带约束系统数值模型Fig.1 The numerical model of the safety belt restraint system

汽车碰撞中乘员因受冲击载荷作用，头、胸及腿部极易发生损伤，而损伤值与安全带约束系统紧密相关。为综合评价约束系统整体性能，采用加权伤害准则WIC(Weighted Injury Criterion)[7]评价安全带约束系统好坏，即

(1)

式中：HIC为头部综合性能指标；C3ms为胸部3 ms加速度值(单位G)；D为胸部压缩量(单位mm)；FFL，FFR为左、右大腿轴向压力(单位kN)。

对汽车安全带约束系统工程优化设计问题而言，会涉及非常耗时的数值分析模型。为此，本文通过径向基函数建立安全带约束系统近似模型，并结合IP-GA遗传算法及近似模型管理方法对系统特性参数进行优化,形成从安全带约束系统数值模型建立-实验验证-参数优化的设计方法。设计流程见图2。

图2　安全带约束系统优化设计流程图Fig.2 The optimization procedure ofsafety belt restraint system

2安全带约束系统数值模型验证

按《乘用车正面碰撞的乘员保护》(GB11551-2003)规定的试验方法及程序进行实车碰撞试验，并通过假人身体各部位数据验证安全带约束系统数值模型的有效性，见图3。

图3　安全带约束系统数值模型与实验模型对比Fig.3 The comparison of the numerical simulation model and experiment model

假人身体各部位动态响应与实验响应曲线对比见图4。若二者重合度较好，则说明该模型准确可靠，否则修改模型的相关参数直到满足要求。由图4看出，假人身体各部位响应曲线数值与实验结果虽存在一定误差，但两者变化趋势吻合较好，峰值出现时间与曲线峰值大小基本一致，能基本反应汽车碰撞过程中人体各部位响应。

图5为假人运动响应仿真与实验的对比，可见二者结果相对一致，表明数值模型及建模方法有效，可进行优化设计。

3安全带约束系统特性参数匹配

3.1安全带约束系统优化问题描述

安全带约束系统约束效能主要体现对人体的保护，故选取WIC作为优化目标函数；将头部综合性能指标HIC值、胸部3 ms加速度值C3ms、胸部压缩量D及左、右大腿轴向压力FFL、FFR作为约束条件；将安全带挂点位置、伸长率及初始应变作为设计变量，优化问题可描述为

(2)

式中：fWIC为加权伤害准则WIC值；gHIC为人体头部损伤HIC值；gC3ms为胸部损伤C3ms值；gD为胸部压缩量D值；gFFL为左大腿轴向压力FFL；gFFR为右大腿轴向压力FFR；X为设计变量，x1为安全带上挂点位置，x2为伸长率，x3为初始应变。

图4　假人动态响应曲线仿真与实验对比Fig.4 The comparison of the dynamic response of the numerical simulation model and experiment model

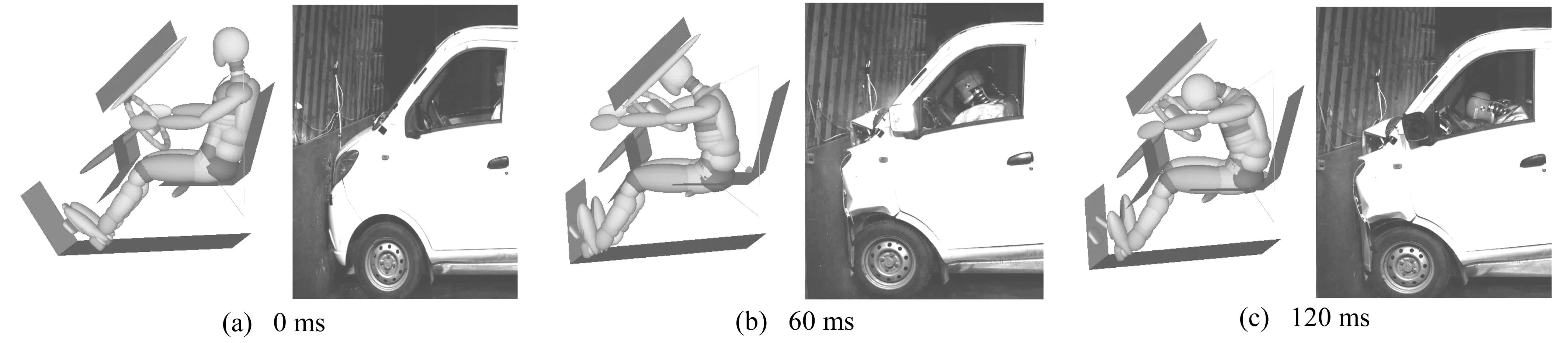
图5　假人运动响应仿真与实验对比Fig.5 The comparison of the motion responseof the numerical simulation model and experiment model

由于汽车安全带约束系统数值分析模型非常复杂，使传统优化方法效率上无法满足设计需要。常采用构造简单的显式函数作为近似模型替代原数值分析模型，并与非线性优化技术结合构造近似优化问题快速计算[8]。本文通过拉丁超立方采样Latin Hypercube Design(LHD)技术获得试验设计样本点，利用径向基函数构建安全带约束系统近似模型，结合IP-GA遗传算法及近似模型管理方法对近似优化问题求解，获得安全带约束系统最佳匹配参数。

3.2试验设计方法

试验设计用于获取构建近似模型所需设计样本。选拉丁超立方采样(LHD)技术作为试验设计方法[9-10]。LHD应用灵活，可任意控制样本集大小，故可饱和采样；LHD样本点可保证在采样空间均匀分布；通过LHD可实现两代设计间样本点遗传，节约计算成本。

3.3径向基函数近似模型

径向函数[11-12]以待测点与样本点间的欧氏距离为自变量。以径向函数为基函数，通过线性叠加构造的模型即为径向基函数模型。利用样本点xi处响应值，通过基函数线性叠加计算待测点x处响应值径向基模型基本形式为

(3)

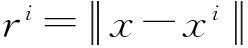
选Gauss函数作为径向函数，即

Φ(r)=exp(-r2/c2)

(4)

式中：c为大于零的常数。

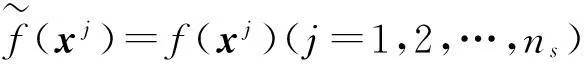
f=Φw

(5)

若Φ的逆矩阵存在，则可得权系数矢量为

w=Φ-1f

(6)

将权系数代入式(3)可得径向基函数近似模型。

3.4近似优化问题建立及求解

用径向基函数构建安全带约束系统近似模型，则式(2)描述的优化问题可转换为数学形式，即

(7)

结合IP-GA遗传算法[13]及近似模型管理方法对安全带约束系统(式(7))近似优化问题进行求解，具体优化流程见图6。

(1)在设计域空间上用LHD采样，调用所有采样点真实数值模型进行计算，获得目标函数及约束初始样本。给定允许误差ε>0，置迭代步数s=1。

(2)利用目标函数及约束样本建立径向基函数近似模型，构建安全带约束系统近似优化问题。用IP-GA遗传算法获得近似优化问题的解X(s)。

(3)计算真实目标函数fWIC及约束函数gHIC，gC3ms,gD,gFFL，gFFR在近似优化设计解X(s)处的值。

(4)计算误差emax

若emax<ε，则输出优化设计解X(s)，迭代终止；否则转下一步。

(5)将当前步的真实目标函数及约束函数在近似优化设计解X(s)处的值作为新样本点加入原目标函数及约束函数样本空间，构成新的样本空间，置迭代步数s=s+1，返回(2)。

图6　优化求解流程图Fig.6 The procedure of optimal design

3.5优化结果及分析

整个优化过程中，允许误差ε=3%，目标函数及约束初始样本点为50个，用IP-GA遗传算法对优化问题进行求解。IP-GA遗传算法参数为:种群大小N=5，交叉概率pc=0.5，变异概率pm=0.02，迭代次数100。

安全带约束系统在每个迭代步的优化结果见表1～表3。由3表看出,整个优化过程共持续3个迭代步。第1迭代步中目标函数及约束函数优化值与仿真值最大误差达16.9%，超过许用误差值3%。说明此时目标函数及约束函数近似模型较粗糙，需将当前步仿真目标函数及约束函数值作为新样本点加入原样本空间，构建精确近似模型。第2迭代步中最大误差由16.9%下降到4.2%,但仍超出许用误差值，近似模型精度需进一步提高。第3迭代步中目标函数、约束函数优化值与仿真值的最大误差为0.9%，低于许用误差值。说明此时目标函数、约束函数近似模型已达较高精度，且在当前优化设计解(0.8615, 0.06273, 0.000)处各项乘员损伤值均在耐受极限范围内，因此优化结果符合设计要求。

表1　第1迭代步优化结果(样本点50个)

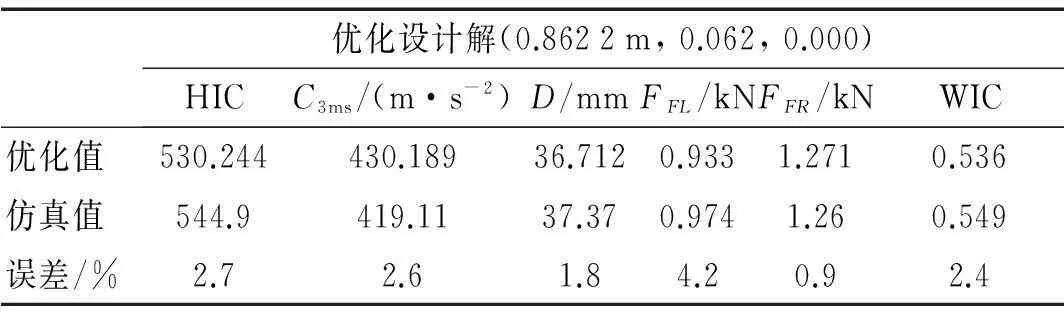
表2　第2迭代步优化结果(样本点51个)

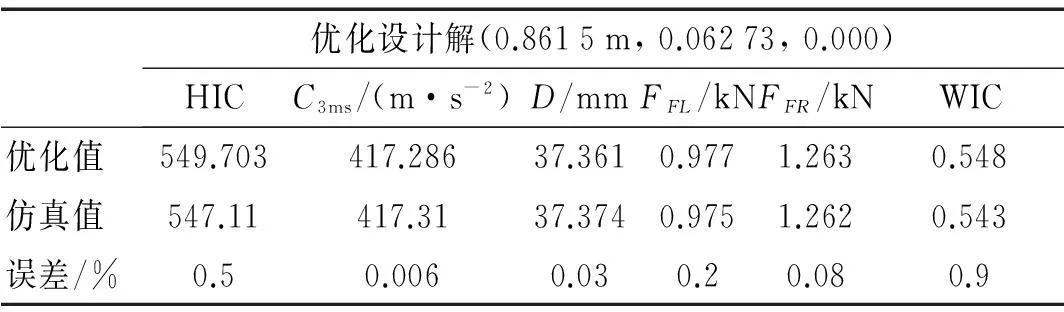
表3　第3迭代步优化结果(样本点52个)

安全带约束系统优化前后防护性能对比见表4。由表4看出，优化前乘员头部综合性能指标HIC值为1 071.4，超出人体头部耐受极限值1 000。优化后，HIC值为547.11，下降48.94%，明显低于耐受极限值。且胸部3 ms加速度值C3m及压缩量D、左右大腿轴向压力FFL及FFR均低于法规阀值。此时加权伤害准则WIC值为0.543，与优化前相比，安全性能提高36.71%。

表4　安全带约束系统优化前后性能对比

4结论

(1)针对某微型客车驾驶室结构，建立汽车安全带约束系统数值模型研究人体损伤响应。在实车碰撞实验基础上，通过与仿真结果对比验证建模方法及数值模型的有效性。

(2) 为提高优化效率，结合拉丁超立方采样技术及径向基函数构建基于近似模型管理的汽车安全带约束系统优化设计方法，不仅能为安全带约束系统优化设计提供特征参数、减少实验次数、降低实验成本，且在汽车被动安全领域具有实际意义。

参 考 文 献

[1] 王蕊,张晓云,冯浩,等.大客车侧翻碰撞护栏事故仿真分析及改进[J].振动与冲击,2014, 33(6):40-43.

WANG Rui, ZHANG Xiao-yun, FENG Hao, et al. Simulation and improvement of bus rollover against barrier[J]. Journal of Vibration and Shock,2014, 33(6): 40-43.

[2] 白中浩,蒋彬辉,张前斌,等. 乘用车-载货汽车追尾碰撞相容性结构优化设计[J].振动与冲击,2011,30(8)：36-40.

BAI Zhong-hao, JIANG Bin-hui, ZHANG Qian-bin,et al. Optimal design of compatible structure for passenger car and truck rear crash [J]. Journal of Vibration and Shock, 2011, 30(8): 36-40.

[3] 曹立波，喻伟雄，白中浩，等. 基于正面碰撞防护的SUV车辆乘员约束系统优化[J].中国机械工程，2011，22(3)：374-378.

CAO Li-bo, YU Wei-xiong, BAI Zhong-hao, et al. Optimization of passenger restraint system of a production SUV based on automobile frontal impact protection[J]. China Mechanical Engineering, 2011, 22(3): 374-378.

[4] 张学荣,刘学军,陈晓东,等. 正面碰撞安全带约束系统开发与试验验证[J]. 汽车工程,2007, 29(12):1055-1058.

ZHANG Xue-rong, LIU Xue-jun, CHEN Xiao-dong, et al. Development and test validation of safety belt restraint system for frontal impact[J].Automotive Engineering,2007,29(12):1055-1058.

[5] 赵志杰,金先龙. 乘员约束系统耐撞性数据挖掘[J]. 振动与冲击, 2010, 29(3):13-17.

ZHAO Zhi-jie, JIN Xian-long. Data mining on crashworthiness data of occupant restraint system[J]. Journal of Vibration and Shock, 2010, 29(3):13-17.

[6] Rajiv P, James C. Integration of vehicle interior models into crash up-front process with optimization[C]//SAE Technical,1995: 951107.

[7] Viano D, Arepally S. Assessing the safety performance of occupant restraint system[C]//SAE Technical,1990: 902328.

[8] Fang H, Rais-Rohani M,Liu Z, et al. A comparative study of metamodeling methods for multi-objective crashworthiness optimization[J]. Computers and Structures,2005,83:2121-2136.

[9] Yang R J, Wang N, Tho C H, et al. Metamodeling development for vehicle frontal impact simulation[J]. Journal of Mechanical Design,2005, 127:1014-1020.

[10] Morris M D, Mitchell T J. Exploratory designs for computational experiments[J]. Journal of Statistical Planning and Inference, 1995, 43 (3): 381-402.

[11] Jin R, Chen W, Smpson T W. Comparative studies of metamodeling techniques under multiple modeling criteria[J].Journal of Structural and Multidisciplinary Optimization, 2001, 23 (1): 1-13

[12] 穆雪峰,姚卫星,余雄庆,等. 多学科设计优化中常用代理模型的研究[J]. 计算力学学报，2005，22(5): 608-612.

MU Xue-feng, YAO Wei-xing, YU Xiong-qing, et al. A surveyof surrogate models used in MDO[J]. Chinese Journal of Computational Mechanics, 2005, 22(5): 608- 612.

[13] Liu G R，Han X. Computational Inverse Techniques in Nondestructive Evaluation[M]. Florida: CRC Press, 2003.

Optimal design of a seat belt restraint system based on approximate model management

LIUXin1,2,WUGang1,YINLai-rong1

(1. Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road & Traffic Safety, Ministry of Education, Changsha University of Science and Technology, Changsha 410004, China;2. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China)

Abstract:In order to improve the protection capability of seat belt restraint systems, a numerical model of seat belt restraint systems was calibrated by vehicle crash experiments and an approximation model was constructed according to the radial basis function. The IP-GA genetic algorithm was employed to optimize the key parameters of the seat belt restraint system dynamic characteristics. To reduce the error from the approximate model, the management framework was used to update the approximate model and control the error in the optimization process. The optimal solutions with errors in given range can be treated as solutions to the problem. It was demonstrated that the proposed method could effectively find the optimal parameters of seat belt restraint systems and ensure their safety.

Key words:safety belt restraint system；approximate model management；optimal design

中图分类号:U461.91

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.024

收稿日期：2014-10-22修改稿收到日期：2015-03-25

基金项目：国家自然科学基金资助项目(51305047);湖南大学汽车车身先进设计制造国家重点实验室开放基金(31315013)项目资助；长沙理工大学道路灾变防治及交通安全教育部工程研究中心开放基金资助项目(KFJ110302)

第一作者 刘鑫 男，博士，副教授，硕士生导师，1981年2月生