基于内积延拓LMD及SVM的轴承故障诊断方法研究

姜久亮， 刘文艺， 侯玉洁， 仲召明， 陈思瑶

(江苏师范大学 机电工程学院，江苏 徐州221116)



基于内积延拓LMD及SVM的轴承故障诊断方法研究

姜久亮， 刘文艺， 侯玉洁， 仲召明， 陈思瑶

(江苏师范大学 机电工程学院，江苏 徐州221116)

摘要：针对特征提取中局域均值分解(Local Mean Decomposition, LMD)存在端点效应缺陷及模式识别中人工神经网络(Artificial Neural Network, ANN)存在收敛速度慢、过学习等不足，提出基于内积延拓LMD及支持向量机(Support Vector Machine, SVM)的轴承故障诊断方法。利用内积延拓LMD方法对信号延拓分解抑制LMD端点效应；利用分解的可描述信号特性主分量PF(Product Function)构建初始特征向量矩阵；用SVD(Singular Value Decomposition)方法对初始特征向量矩阵进行奇异值分解，获得信号特征参数作为SVM的输入进行训练；对训练的SVM进行测试及模式分类。通过实际轴承故障信号分析及故障类型分类表明，该方法不仅能抑制LMD端点效应缺陷，且在故障模式识别中能有效避免ANN网络结构难确定、收敛速度慢等不足，能较好实现轴承故障准确分类，可用于轴承故障诊断。

关键词：内积延拓局域均值分解；奇异值分解；支持向量机；滚动轴承；故障诊断

滚动轴承作为旋转机械中应用最广泛的部件，因长时间不间断运行极易发生机械故障，会直接影响整个机械的性能及安全。轴承故障诊断主要有信号处理及模式识别。对信号处理分析、提取特征频率主要为时频分析法，如短时傅里叶变换(Short Time Fourier Transform, STFT)[1]、Hilbert变换[2]、Wigner-Ville分布(WVD)[3-4]、经验模式分解(Empirical Mode Decomposition, EMD)[5-6]等。局域均值分解(LMD)作为新的非平稳信号处理方法已广泛用于机械故障诊断，并取得较好成果[7-9]。而该方法存在端点效应缺陷，致分解所得信号两端出现摆动、失真现象，甚至无法有效提取故障特征。端点延拓方法亦存在缺陷：如自适应三角波匹配法[10]及AR模型延拓法[11]均缺少对信号的整体认识，无法从算法原理本身进行抑制；故障模式识别主要有人工神经网络(ANN)与支持向量机(SVM)两种方法。ANN具有良好的映射逼近能力、并行处理能力、较强自学习能力、自组织性、自适应性等优点已用于机械故障诊断[12-14]。ANN存在学习网络结构难以确定、收敛速度慢及训练需大量数据样本等缺陷。而SVM作为新模式识别方法能有效克服ANN结构难以确定、过学习等问题。Ma等[15]运用SVM方法实现对滚动轴承的故障分类。Zhang等[16]将EEMD与SVM结合用于轴承滚动故障诊断。Liu等[17]用SVM实现齿轮故障诊断。Sugumaran 等[18]将基于临近点核函数的多分类支持向量用于滚动轴承故障分类。利用SVM实现故障准确分类，其中最重要的即为确定输入参数，使其能准确反映故障特征类型及简便提取。对轴承故障类型分类，由于采集的故障振动信号频域成分较复杂，直接作为SVM特征参数往往得不到理想效果。由矩阵理论知，矩阵奇异值为其固有特性，元素发生较小改变时矩阵奇异值几乎不变，描述矩阵特征向量的内在特性，可用于分析轴承运行状态。

本文提出基于内积延拓LMD及SVM的轴承故障诊断方法。从信号内部规律着手对原始信号进行内积延拓，使延拓后信号保持原始信号的自然趋势并进行LMD分解，以所得故障信号分解主分量PF(Product Function)构建原始特征向量矩阵；利用奇异值分解(SVD)方法获取原始特征向量矩阵奇异值作为SVM的输入参数，对SVM进行训练；并测试训练好的SVM及识别故障类型，达到轴承故障诊断目的。

1内积延拓LMD方法

由LMD算法原理[19]知，第1个迭代循环获取纯调频信号时需先获取原始信号的局域均值函数及局域包络函数，再进行算法后续循环。而信号局域均值函数m11(t)及包络函数a11(t)的获取可通过计算信号极值及平滑处理获得，即

(1)

(2)

式中：ni为第i极值点；mi，ai为两相邻极值点局域均值及幅值。

利用直线将所得全部局域均值、幅值连接，并进行平滑处理获得信号的局域均值函数m11(t)及包络函数a11(t)。图1为给定的待分析信号，其中空圆点表示信号极值点。由图1中看出，该信号由具有较强规律的信号中截取，两端值并非该信号极值。用式(1)、(2)计算局域均值、幅值时LMD方法默认将信号两端值视为极值，直接导致局域均值函数及包络函数误差，进而影响后续算法循环误差，此为导致LMD端点效应的根本原因。

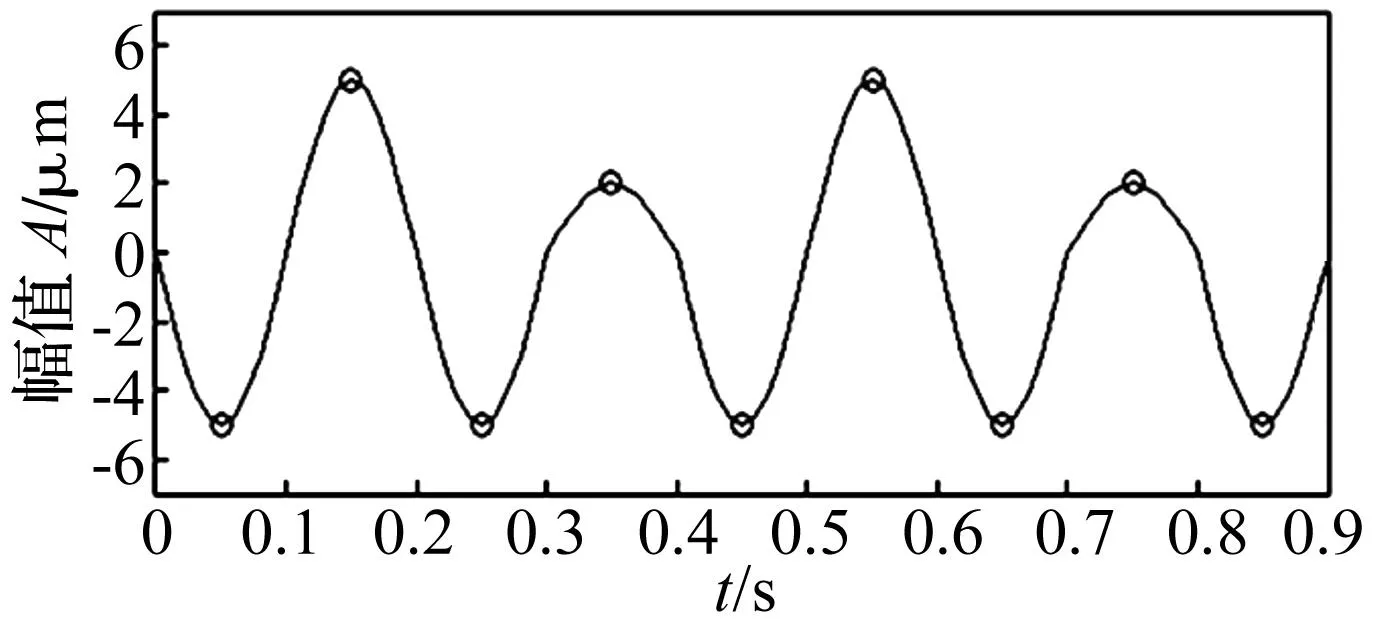
图1　待分析信号Fig.1 The anlysis signal

针对LMD算法特点及信号内部固有规律特性，提出采用内积延拓方法对LMD待分析信号进行左右延拓，原理见图2。其中两条竖虚线间波形为原始待分析信号时域波形，小圆空点为该信号所有极值点；左侧点划线波形为延拓的最优匹配波形，对应的实线为原始信号内部分曲线；右侧浅色点划线为延拓最优匹配波形，对应的实线为原始信号内部分曲线。

图2　内积延拓LMD方法原理Fig.2 The Schematic diagram of LMD end extension method based on integral local waveform matching

信号延拓包括左、右延拓两种，以左延拓中待分析信号第1极值点为最大值详述该方法的基本原理如下：

(1)以信号左端点与其后两极值点间波形构建特征波形x1-xm1-xn1，计算积分值a，即

(3)

式中：x1为信号左端点值；xm1，xn1为第1极大、极小值；tn1为第1极小值点对应时间。

(2)利用相似比计算所有相似波形起点值时间，即

(4)

式中：tni，tmi为第i个极小、极大值点对应时间；txi为相似波形起点值对应时间。

(3)以每个相似波形起点与其后两极值点构建相似波形xi-xmi+1-xni+1计算积分值bi，即

(5)

式中：ti为第i个相似波形起始点时间；tni+1为第i+1个极小值对应时间。

(4)利用求差运算计算所有相似波形积分值与特征波形积分值差，并对结果取绝对值，即

(6)

(5)获取匹配波形，比较差值ei确定最小差值对应的i并赋予c，即

c=i(min(ei)),(i=1,2,3,…)

(7)

则c对应的相似波形即为匹配波形。

(6)将匹配波形前信号即图2中深色波形延拓到信号左端，即为延拓波形(左端虚线波形)；右延拓方法类似。

可见该方法充分考虑信号每点的信息及内部规律，使延拓后信号保持原始趋势。

2SVM分类原理

SVM由在两类样本中寻找最优超平面发展而来[20]，见图3。图中五角星及圆点表示两类样本；H为分类线也称分类超平面；H1，H2分别为过各类中离分类线最近样本且平行于分类线直线。设该分类超平面H的方程为

wx+b=0

(8)

式中：w为分类面权系数向量；b为分类阈值。

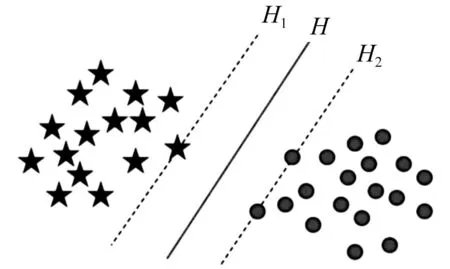
图3　SVM分类原理Fig.3 The classification principle of SVM

由图3看出，将两类样本分开的超平面并非唯一，必存在最优超平面，使样本中所有数据到该分类平面距离最大，该平面即最优超平面。

L(w,b,α)=

(9)

式中：αi为Lagrange系数。

将式(7)分别对w，b求偏微分并令其等于0，即将原问题转化为对偶问题，即

(10)

αi≥0, (i=1,2,3,…)

(11)

在式(8)、(9)约束条件下求解函数最大值，即

(12)

最优分类函数为

f(x)=sgn{(wx)+b}

(13)

对非线性问题可通过非线性变换转化为高维空间的线性问题，在高维空间中寻找最优超平面，而核函数可较好解决。只要在最优分类面中用适当的核函数K(xi,yi)即可实现从低维到高维的转换，实现非线性SVM分类。此时目标函数变为

(14)

最优分类函数变为

(15)

所选核函数不同获得支持向量机也不同。目前常用分类核函数主要有4种，即①线性核函数K(x,y)=xy；②多项式核函数K(x,y)=(xy+1)d，d=1,2,3,…;③径向基核函数K(x,y)=exp{-‖x-y‖2/2σ2}，其中σ为函数宽度参数；④Sigmoid核函数K(x,y)=tanh[v(xy)+c]，其中v，c为比例、偏移参数。

3基于内积延拓LMD、SVM的轴承故障诊断方法

轴承故障诊断特征提取中因其频域分布较复杂，直接用作特征参数往往难以达到理想效果。矩阵SVD所得奇异值为其固有特性，其中元素发生较小变化时矩阵奇异值几乎不变，可用于描述轴承运行状态。因此本文提出基于内积延拓LMD及SVM相结合的轴承故障诊断方法。选取内积延拓LMD分解轴承故障信号获得PF分量构成的矩阵奇异值作为描述轴承运行状态特征参数训练SVM。具体流程见图4。

图4　基于内积延拓LMD及SVM轴承故障诊断方法流程图Fig.4 The Schematic diagram of the method based on SVM and the LMD extension method based on integral local waveform matching

图4执行步骤为：①获取滚动轴承正常、内外圈故障3种状态振动信号，分别进行N次采样，获得3N个滚动轴承振动信号作为训练样本；②对采集的所有样本振动信号分别进行内积延拓并进行LMD分解，获得每个样本信号分解PF主分量；③构建初始特征向量矩阵，分别对每个样本信号的内积延拓LMD分解结果PF主分量构建初始特征向量矩阵A，格式为A=[PF1PF2PF3PF4…]T；④对所得每个初始特征向量矩阵A进行SVD获得特征参数σ；⑤σ输入SVM进行训练；⑥重复以上步骤获取轴承3种运行状态的测试样本及特征参数，将特征参数输入训练好的SVM中进行测试及故障类型识别，验证该方法的有效性。

4实验研究

本实验滚动轴承振动信号训练、测试样本数据源自Case Western Reserve University轴承数据库[21]。实验所用训练样本由数据中任意选取，由正常轴承、内、外圈故障轴承数据中各选3组，每组1 024个数据点，共9组训练样本，用于训练SVM。测试样本每种类型选3组，每组测试样本数据点1 024，用于测试信号分类识别。

利用训练样本对SVM进行训练。选9组训练样本分别进行内积延拓LMD分解，其中2组样本信号内积延拓LMD分解结果前3主分量见图5、图6。由两图看出，轴承内外圈故障样本信号分解的3主分量PF两端均未出现摆动、失真现象，表明抑制LMD端点效应较好。

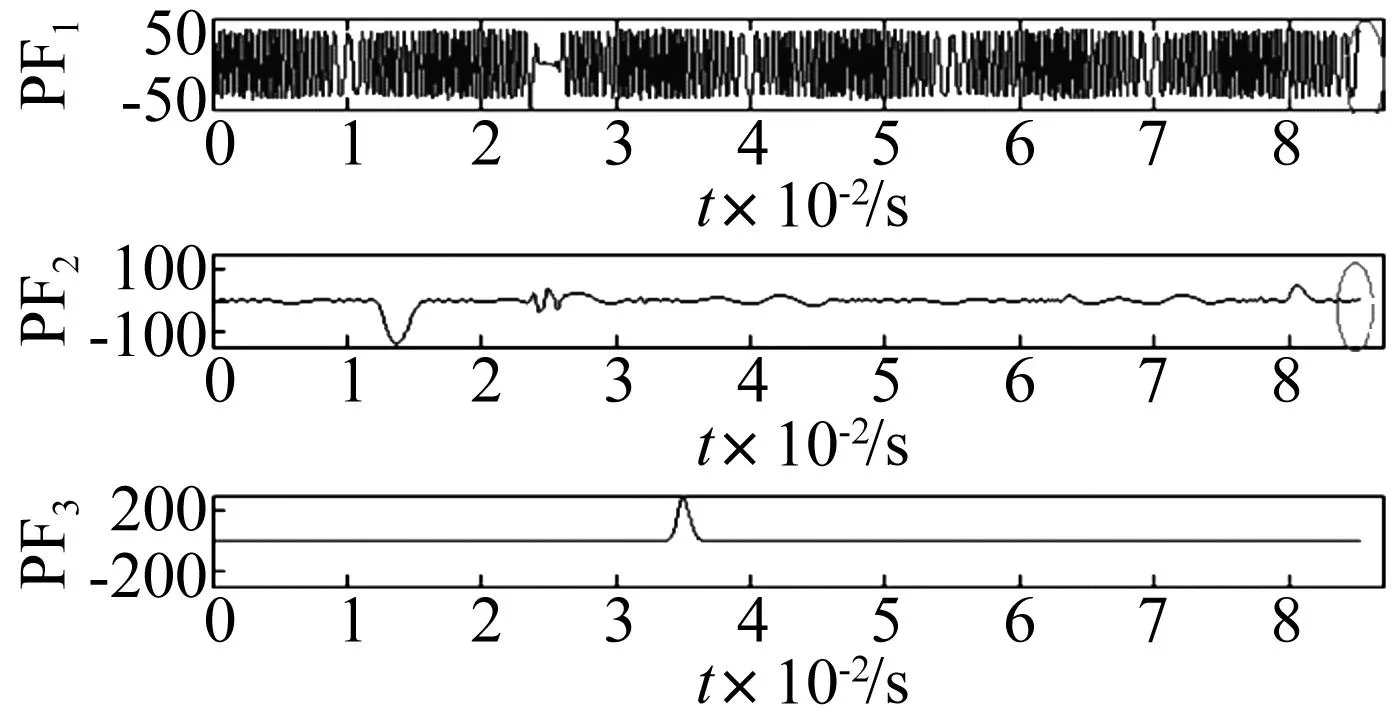
图5　内圈样本信号内积延拓LMD结果Fig.5 The LMD results of the inner fault signal by the extension method based on integral local waveform matching

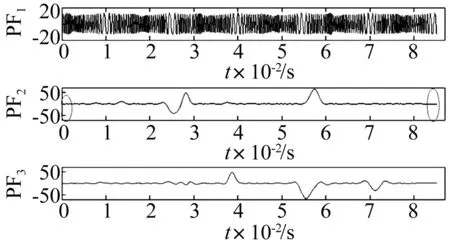
图6　外圈样本信号内积延拓LMD结果Fig.6 The LMD results of the outer fault signal by the extension method based on integral local waveform matching

为进一步证明该方法的优势，分别选分解的前3主分量PF迭代次数及分解层数进行与LMD方法研究对比，结果见表1、表2。由两表看出，无论外圈或内圈故障信号，获得前3主要分量PF迭代次数或分解层数，内积延拓LMD方法少的多。即内积延拓LMD方法较LMD方法分解效率更高。

表1　内圈样本信号分解性能指标

表2　外圈样本信号分解性能指标

利用样本信号分解的PF主分量构建初始向量矩阵。由于轴承故障特性主要集中于前几个PF主分量，因此本文取分解结果的前4个PF分量构建初始向量矩阵A，对所有初始向量矩阵进行SVD，获得所有特征参数σ，再将特征参数作为3个SVM输入元素用高斯径向核函数进行SVM训练，将训练数据中属于正常轴承(3组)视为一类，记为+1；其余6组训练样本视为一类，记为-1，建立SVM1；采用相同方法建立SVM2、SVM3。其中SVM2用于判别轴承内圈故障，SVM3用于判别轴承外圈故障，不属于以上3种的则认为分类错误，两个分类器同时出现+1时则认为无法进行分类识别。建立3个SVM后在对测试样本进行分类识别时，若其中1个分类器为+1另两个均为-1时，则认为该分类器识别成功。9组训练样本奇异值特征参数见表3。

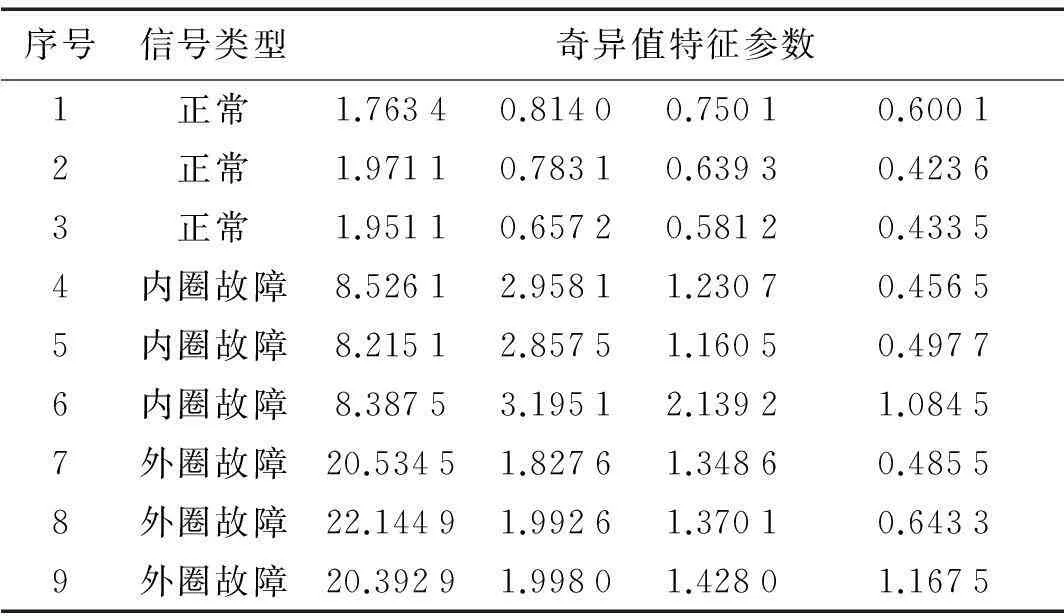
表3　基于内积延拓LMD及SVM的滚动轴承特征参数

利用相同方法获得3种轴承故障类型振动信号9组测试样本的输入特征参数，将其输入训练好的SVM中进行测试分类识别，结果见表4。由表4看出，训练好的SVM对随机选的3种轴承类型9组测试样本信号进行分类识别结果均正确，正确率达100%，因此可将正常轴承、内外圈故障轴承进行正确分类。

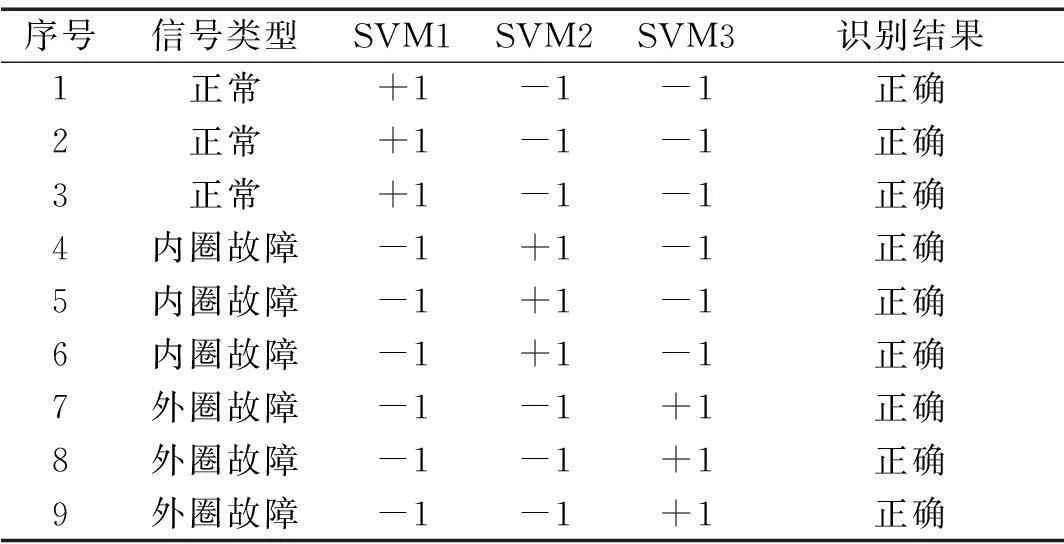
表4　SVM轴承故障识别结果

5结论

利用所提基于内积延拓LMD、SVM的轴承故障诊断方法对实际轴承故障信号分析，结论如下：

(1)内积延拓LMD法能较好抑制LMD端点效应，分解效率更高；轴承故障信号特征向量奇异值能较好描述轴承的运行状态。

(2)内积延拓LMD、SVM相结合不仅能克服ANN网络结构难确定、过学习等不足，且能准确实现滚动轴承的故障分类，可用于轴承故障诊断。

参 考 文 献

[1] Chen M, Ma B. Fault diagnosis of wet-shift clutch based on STFT and wavelet[J]. Advanced Materials Research, 2011,301/302/303: 1560-1567.

[2] Michael F. Hilbert transform methods for nonparametric identification of nonlinear time varying vibration systems[J]. Mechanical Systems and Signal Processing, 2014,47(1/2):66-77.

[3] Bin G F, Liao C J, Li X J. The method of fault feature extraction from acoustic emission signals using Wigner-Ville distribution[J].Advanced Materials Research, 2011,216:732-737.

[4] Tang B P, Liu W Y, Song T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution [J]. Renewable Energy, 2010,35(12): 2862-2866.

[5] Sun M Z, Tang H T. Mixed programming realization of the EMD-WVD combined method[J]. Telkomnika-Indonesian Journal of Electrical Engineering, 2013(11): 1902-1908.

[6] Zhong X Y,Zhao C H,Dong H J,et al. Rolling bearing fault diagnosis using sample entropy and 1.5 dimension spectrum based on EMD[J]. Applied Mechanics and Materials, 2013,278/279/280:1027-1031.

[7] 孙伟，熊邦书，黄建萍，等.小波包降噪与LMD相结合的滚动轴承故障珍断方法[J].振动与冲击, 2012,31(18): 153-156.

SUN Wei, XIONG Bang-shu, HUANG Jian-ping,et al. Fault diagnosis of a rolling bearing using wavelet packet denosing and LMD[J]. Journal of Vibration and Shock,2012,31(18): 153-156.

[8] Ma J, Wu J D, Yuan X Y. The fault diagnosis of the rolling bearing based on the LMD and time-frequency analysis[J]. International Journal of Control and Automation, 2013(6):357-376.

[9] Dong Z S, Tian X Q. Mechanical fault diagnosis based on LMD-approximate entropy and LSSVM[J]. Telkomnika-Indonesian Journal of Electrical Engineering, 2013(11):803-808.

[10] 王录雁,王强,鲁东林,等．EMD自适应三角波匹配延拓算法[J]．振动与冲击,2014,33(4): 94-99.

WANG Lu-yan, WANG Qiang, LU Dong-lin, et al. A self-adaptive triangular waveform matching extension algorithm for EMD[J]. Journal of Vibration and Shock, 2014, 33(4): 94-99.

[11] 胥永刚,陆明,付胜,等.基于匹配延拓的ITD边界效应抑制方法研究[J]．振动与冲击,2014,33(7):165-169.

XU Yong-gang, LU Ming, FU Sheng, et al. End effect restrained method of intrinsic time-scale decomposition based on matching extension[J]. Journal of Vibration and Shock,2014,33(7):165-169.

[12] Zhu Q, Li J. Applied technology on artificial neural network in fault diagnosis system[J]. Advanced Materials Research, 2014,859: 448-452.

[13] Khan A A S, Chowdhury A R. Monitoring and detecting health of a single phase induction motor using data acquisition interface (DAI) module with artificial neural network[J]. WSEAS Transactions on Systems and Control, 2014(9): 229-237.

[14] Shatnawi Y, Al-Khassaweneh M. Fault diagnosis in internal combustion engines using extension neural network[J]. IEEE Transactions on Industrial Electronics, 2014,61(3):1434-1443.

[15] Ma J, Wu J D. Fault diagnosis of rolling bearing based on the PSO-SVM of the mixed-feature[J]. Applied Mechanics and Materials,2013, 380/381/382/ 383/384: 895-901.

[16] Zhang M J, Chai K. Combined improved EEMD with SVM in the bearing low dimensional small sample fault diagnosis[J]. Applied Mechanics and Materials, 2013,427/428/429:354-357.

[17] Liu J M, Liu Y H. A research on the fault diagnosis of transmission gears based on complex modulation zoom envelope spectrum and SVM[J].Qiche Gongcheng/Automotive Engineering, 2014(36): 608-612.

[18] Sugumaran V, Sabareesh G R, Ramachandran K I. Fault diagnostics of roller beraing using kernel based neighborhood score multi-class support vector machine[J]. Expert Systems with Application, 2008(34): 3090-3098.

[19] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005 (2):443-454.

[20] Cortes C, Vapnik V N. Support vector networks[J]. Machine Learning, 1995(20): 273-297.

[21] http://csegroups.case.edu/bearingdatacenter/pages/download-data-file[DB/OL].

Bearing fault diagnosis based on integral waveform extension LMD and SVM

JIANGJiu-liang,LIUWen-yi,HOUYu-jie,ZHONGZhao-ming,CHENSi-yao

(School of Mechanical and Electrical Engineering, Jiangsu Normal University, Xuzhou 221116, China)

Abstract:Aiming at reducing the end effect of Local Mean Decomposition(LMD) in feature extraction and overcoming the disadvantages of slow convergence and over learning of Artificial Neural Network(ANN) in pattern recognition, a bearing fault diagnosis method was proposed based on the integral waveform extension LMD and the Support Vector Machine(SVM). The analyzed signal was entended and decomposed by the method based on integral waveform extension LMD to inhibit the end effect. The main component product functions (PFs), describing the signal characteristics, was used to establish an initial eigenvector matrix, which was then decomposed by the Singular Value Decomposition (SVD) method to achieve characteristic parameters and train the SVM. The trained SVM was made in use to test and pattern classify. Through actual bearing fault signals analysis and fault types classification, it is indicated that the method can not only inhibit the LMD end effects, but also avoid the ANN disadvantages. It can realize the fault types classification accurately. The method can be used in bearing fault diagnosis.

Key words:integral waveform extension LMD; SVD; SVM; roll bearing; fault diagnose

中图分类号:TP391.9；TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.019

通信作者刘文艺 男，博士，硕士生导师，1984年生

收稿日期：2014-12-26修改稿收到日期：2015-03-25

基金项目：国家自然科学基金(51505202)；江苏省自然科学基金(BK20140238)；江苏省高校自然科学基金(14KJB460014)；江苏师范大学研究生科研创新计划重点项目(2014YZD017)；徐州市科技计划项目(KC15SH054)

第一作者 姜久亮 男，硕士生，1990年生

E-mail: liuwenyi1984@126.com