泥石流浆体与固体颗粒冲击信号能量分布研究

何晓英， 陈洪凯， 唐红梅

(重庆交通大学 岩土工程研究所，重庆　400074)



泥石流浆体与固体颗粒冲击信号能量分布研究

何晓英， 陈洪凯， 唐红梅

(重庆交通大学 岩土工程研究所，重庆400074)

摘要：用小波分析方法对5种浆体黏度、5种固相比与4种颗粒粒径组合的85组泥石流冲击室内模型实验所得冲击信号进行消噪、时频处理，通过对降噪的泥石流冲击信号进行冲击能量计算并分析实验中泥石流冲击能量与频谱间关系。结果表明，随浆体黏度、固相比及颗粒粒径增大，泥石流冲击信号能量呈增长趋势，且相同浆体黏度下固体颗粒粒径大于1.3～1.5 cm时，泥石流冲击能量增幅明显。将冲击信号分解为9个频段(0～1.958 Hz、1.958～3.906 Hz、3.906～7.812 Hz、7.812～15.625 Hz、15.625～31.25 Hz、31.25～62.5 Hz、62.5～125 Hz、125～250 Hz、250～500 Hz)，泥石流冲击信号96%以上能量聚集在频率0～1.958 Hz的低频段a8内。该结果对推动泥石流动力特性研究具有积极意义。

关键词：泥石流冲击；能量分布规律；模型实验；浆体黏度；固相颗粒

我国西部及其它山地、丘陵地区长期存在泥石流病害，尤其公路沿线的桥涵、隧道，严重威胁交通运输[1]。由于泥石流中固液两相介质的运动速度不相等，会发生碰撞、牵引、拖曳，使泥石流体的动、势能随运动发生改变。因此泥石流冲击过程亦伴随冲击能量的变化。

对泥石流冲击能量研究主要集中于：①泥石流运动过程中的能量变化与物质输移。Iverson等[2]认为泥石流运动是熵增过程，运动能量与泥石流体的物理特征关系密切；陈洪凯等[3]从泥石流浆体性质、固相颗粒级配及体积分量、沟床比降、边界条件等方面用两相流观点分析泥石流运动能量消散的微观机理，包括泥石流浆体粘滞作用、固相颗粒碰撞作用及沟床边界摩擦作用等，初步建立能量衰减量计算公式；王兆印[4]通过现场实验及颗粒运动能量分析泥石流龙头运动能量规律，建立龙头运动的能量理论及泥石流运动速度计算公式；舒安平等[5]用泥石流固相与液相的能坡损失之和表达泥石流能量耗损总值，用现场实验实测数据研究分析分界粒径与最小能量耗损及容重间的变化规律。②泥石流灾害评价与基于消能结构的泥石流防治工程设计。由于泥石流为爆发突然、能量巨大的地质灾害，因此危险性评价及工程防治均与泥石流能量相关。如曾超[6]选近似冲击能量的泥石流强度指标IDF，统计5种强度下建筑物产生完全破坏到淤埋损坏的可能性，形成单沟泥石流易损性评价方法；冯泽深等[7]基于能量线性模型分析泥石流输移时的各种能量消耗，从控制能量或熵消耗角度出发，提出通过减少固体物质来源量、增大摩擦两种途径的泥石流减灾措施；王兆印等[8]从能量角度出发，研究阶梯-深潭系统作为新的泥石流消能结构在阶梯、水跃段耗散水流大量能量,使水流中能量减小到不足以触发泥石流。因此，分析泥石流冲击过程中能量特征对全面认识其固液两相冲击特性及防治工程结构安全均具有积极意义。

由于泥石流冲击过程的紊动性，能量信号不易获取及分析，而小波包良好的时频局部化性质使之成为处理信号及能量分析的重要手段，已广泛用于爆破等动力过程分析，如李万等[9]针对某水下目标抗水下爆炸的实验，利用小波包对被监测目标内部装置的冲击加速度信号进行能量分析，获得冲击信号能量分布处于较宽频率范围；Zhong等[10]用小波包能量频谱分析爆破参数在结构动力响应爆破过程中对振动能量频率带分布影响，建立考虑振动强度、频率、持时等因素的结构振动安全判据。而以上对泥石流冲击信号研究中均未用小波分析方法，仅文献[11]用db小波进行水石流冲击特性模型试验，并对所得冲击信号进行消噪、频谱与能量特征分析。

本文实施浆体黏度及级配颗粒组合条件下的泥石流冲击模型实验，采用小波转换方法分析泥石流冲击信号的能量谱特征，探讨泥石流冲击信号能量分布特性。以期为丰富泥石流动力学过程及工程防治提供支持。

1泥石流冲击模型实验

泥石流冲击与运动特性模型采用的水槽实验不能反映泥石流真实运动状态。本文通过30多处现场调查、分析，选西昌-木里干线公路雅砻江河谷中游平川泥石流为原型，在重庆交通大学泥石流动力模型实验场地修筑形状与坡度相似沟谷泥石流实验模型。泥石流主沟槽长15 m，平均沟槽宽0.5 m，深0.6 m，高差3.6 m；布设两个弯道，坡度分别为27°、10°。沟槽顶端为水源箱，储水量1.5 m3；水源箱出口放置木质结构碎石漏斗，体积0.26 m3。泥石流沟口设置动态应力传感器记录泥石流冲击信号，见图1、图2。

图1 实验模型设计平面图Fig.1Planeviewofthetestingmodel图2 泥石流冲击模型实验现场Fig.2Impactingtestofdebrisflow

材料选5组泥石流浆体黏度(η)、5组固相比(r)及4组颗粒粒径(d)，实验工况为Cηrd(η=1，2，3，4，5；r=1，2，3，4，5；d=0，1，2，3，4)。其中，η=1，2，…，5指泥石流浆体黏度分别为0(清水)，0.13 Pa·s，0.37 Pa·s，0.72 Pa·s，0.93 Pa·s；r=1，2，…，5指泥石流固相比(固相颗粒与泥石流体积比)分别为0、0.02、0.04、0.08、0.16；d=0，1，2，…4指泥石流固相颗粒分别为无固相颗粒、粒径0.075～0.2 cm河沙、0.3～0.5 cm瓜米石、0.8～1.0 cm及1.3～1.5 cm碎石。如C234指黏度0.13 Pa·s、固相比0.04、颗粒径1.3～1.5 cm的碎石工况。固相比为0即r=1时d只能等于0，不存在d=1,2,3,4情况，因此时既然无固相颗粒，也不存在颗粒径，如C310指浆体黏度0.37 Pa·s的纯泥浆；而η=0时r=d=0指清水流。

因此，据η、r、d的正交组合，有效实验工况共85组。泥石流浆体黏度用淀粉醚、熟胶粉与水配比而成，用NDJ-1旋转黏度计测定配制的泥石流浆体，使其达到预期黏度要求[12]。固相颗粒粒径0.075～0.2 cm组用河沙，0.3～0.5 cm组用瓜米石，0.8～1.0 cm与1.3～1.5 cm组分别选对应粒径的碎石。据此配置所得泥石流体不同工况密度见表1。

选HS800型动态应力传感器接收泥石流冲击荷载，精度5‰，传感器尺寸见图3；DH5922动态信号测试系统记录冲击荷载信号变化过程，采样频率设为1 000 Hz；Fastcam-ultimal024型号高精度摄像仪记录泥石流运动过程，精度400 fpt。

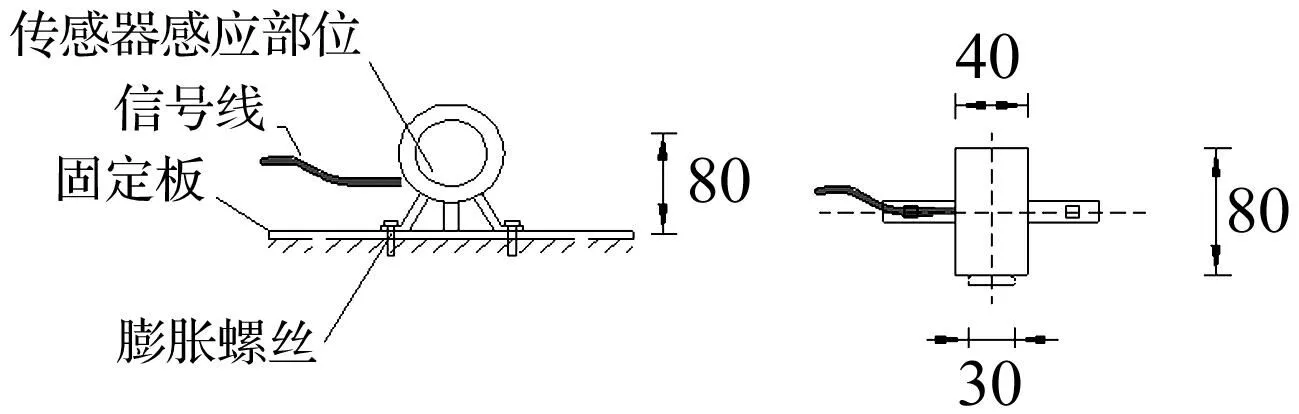
图3　传感器示意图(mm)Fig.3 The schema of the sensor(mm)

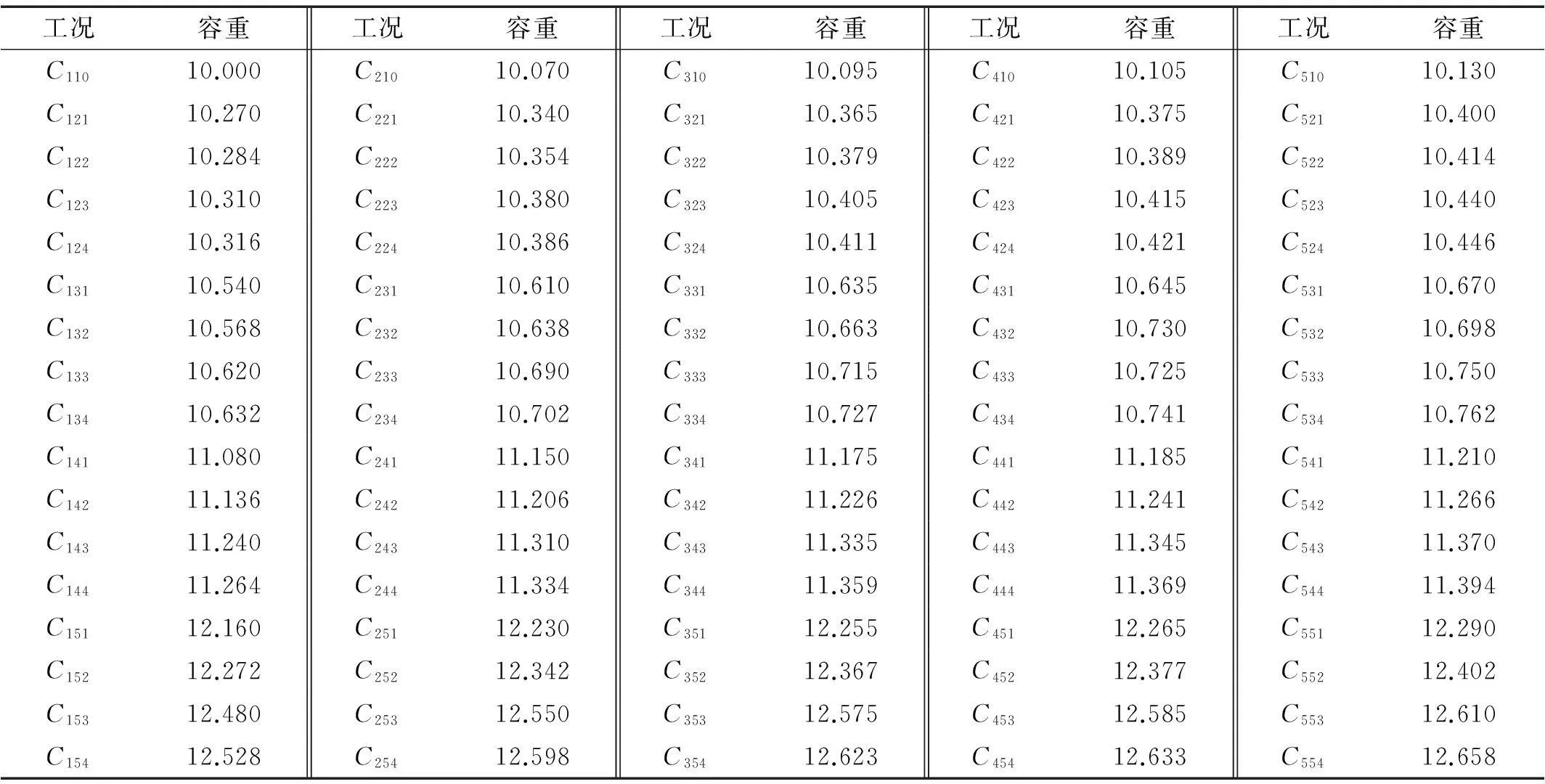
kN/m3

2泥石流冲击信号的小波处理

2.1泥石流冲击信号的小波消噪

传感器采集的泥石流冲击信号中含真实信号与噪音，设冲击信号为一维信号，表达式为

s(t)=f(t)+εe(t)，(t=0,1,2,…,n-1)

(1)

式中：s(t)为传感器接收的含噪信号；f(t)为泥石流冲击真实信号；e(t)为高频噪声信号；ε为系数。

由于泥石流冲击信号为非平稳信号，随机性较强的流体冲击脉动荷载，db小波具有正交性，对该类信号重构可获得较好的平滑效果，且db小波具有阶数越高规则性越高的特性，因此本实验用db8小波对信号进行8层一维多尺度分解降噪处理，按小波分解→小波系数提取→小波重构步骤对信号进行消噪。

为评价降噪效果，用信噪比(SNR)分析信噪比为有效信号功率与噪声信号功率之比，数学表达式为

SNR=10lg(powersignal/powernoise)

(2)

(3)

降噪后信噪比越大降噪效果越好。以C121工况为例，计算得信噪比为24.904，可见降噪效果良好。

2.2泥石流冲击信号频谱特征

冲击信号经小波分解后获得9层频段信号，即

f(t)=a8+d8+d7+d6+d5+d4+d3+d2+d1(4)

式中：a为近似系数；d为细节系数；下标1～8为小波分解层数(尺度数)。

对小波分解后的重构波形进行快速傅里叶变换(FFT)获得频谱图。以工况C431为例，分解的9个频率带频谱见图4，频谱图特征见表2。分析可见，该工况泥石流最大冲击压力(12.162 kPa)位于低频近似系数a8，即泥石流冲击力信号主要为低频信号；而在细节系数频段d1～d8内仅含少量冲击信号，且幅值随频率增高逐渐衰减。1.958～15.625 Hz频段内冲击信号细节呈陡立的单峰形态，15.625～62.5 Hz内呈低矮单峰形态，62.5～500 Hz内冲击信号频谱细节特征逐渐由单峰形态变为双峰形态。

表2　泥石流冲击信号频谱特征

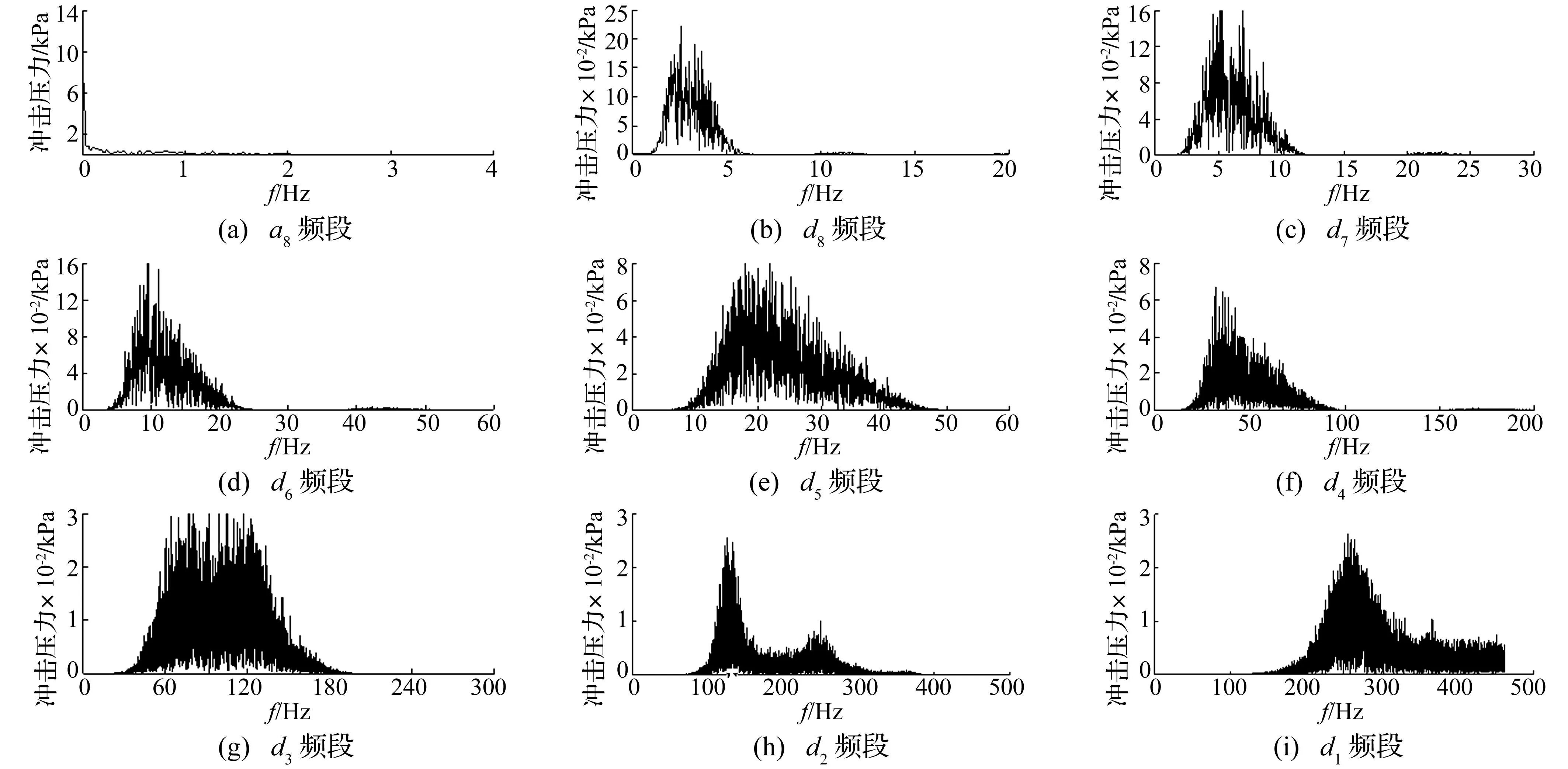
图4　C341工况冲击信号分解后频谱图Fig.4 Analytical spectrum of C341 impacting load

3泥石流冲击信号能量特征

小波方法时间、频率窗可将泥石流冲击信号s(t)分解成不同频率成分，并可分析任一细节，因此能有效分析信号的瞬态特征及频率成分[13]。

采用小波包对各频段冲击信号进行能量分析，获得较准确各频率特性及能量规律，即

(5)

式中：E0为冲击信号总能量(J)；x(t)为原始信号；fi(t)为经分解的各频段信号。

各频段信号能量为

(6)

由此可得不同频段冲击信号相对能量分布为

E=(Ei/E0)×100%

(7)

式中：E为冲击信号相对能量百分比。

通过MATLAB对上式编程，将85组冲击信号进行频谱、能量分析，获得各工况总能量与各频段能量分析结果见图5、表3，近似系数a8频段冲击能量见图6，细节系数(d1～d8)频段总能量见图7。各图中横坐标指同一浆体黏度η条件下不同固相比与不同固相颗粒粒径的组合工况，1～4指r=0.02时固相颗粒径d分别为0.075～0.2 cm、0.3～0.5 cm、0.8～1 cm、1.3～1.5 cm；5～8指r=0.04时固相颗粒径d分别0.075～0.2 cm、0.3～0.5 cm、0.8～1 cm、1.3～1.5 cm；以此类推，0指纯浆体，c1～c5为黏度从0～0.93浆体。

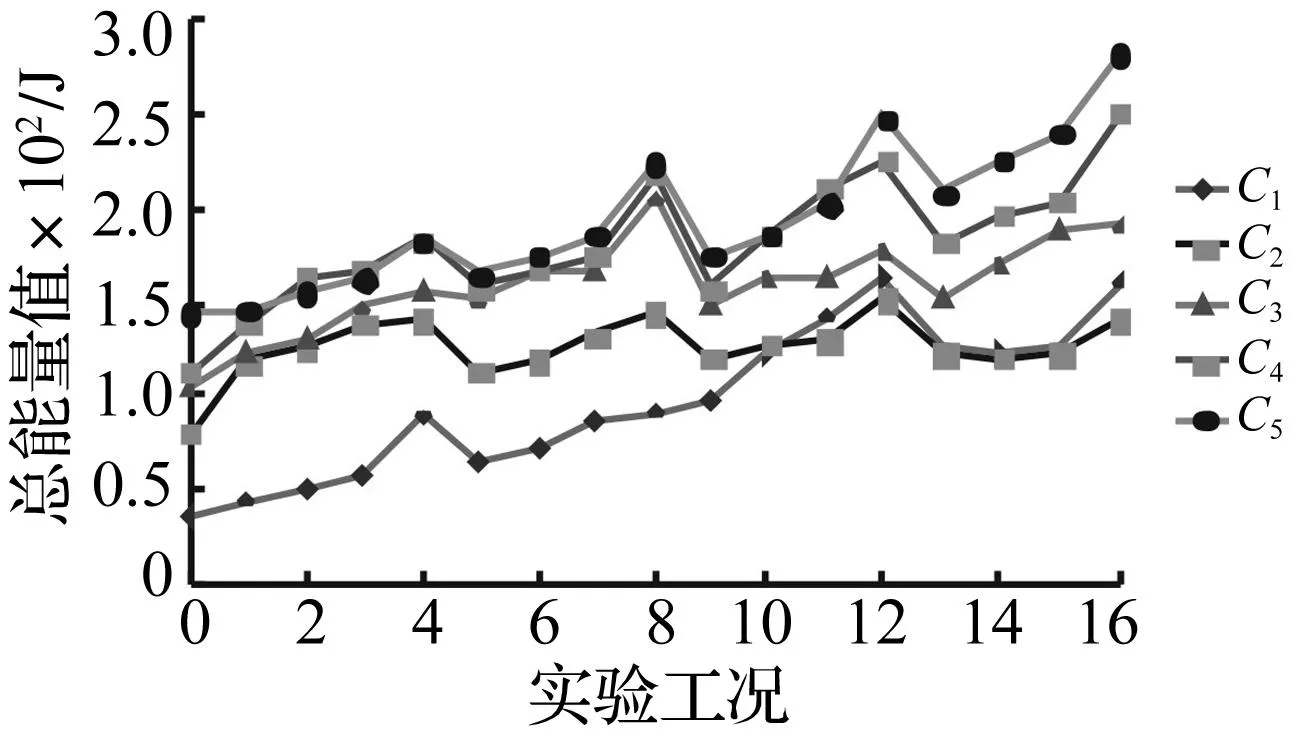
图5　泥石流冲击信号总能量Fig.5 The total energy of impacting signals of debris flow for each condition

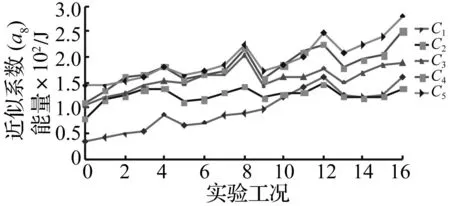
图6　泥石流冲击信号a8频段能量Fig.6 Energy of impacting signals at a8band for each condition

图7　泥石流冲击信号细节系数频段总能量Fig.7 The total energy of impacting signal of debris flow at band under each condition

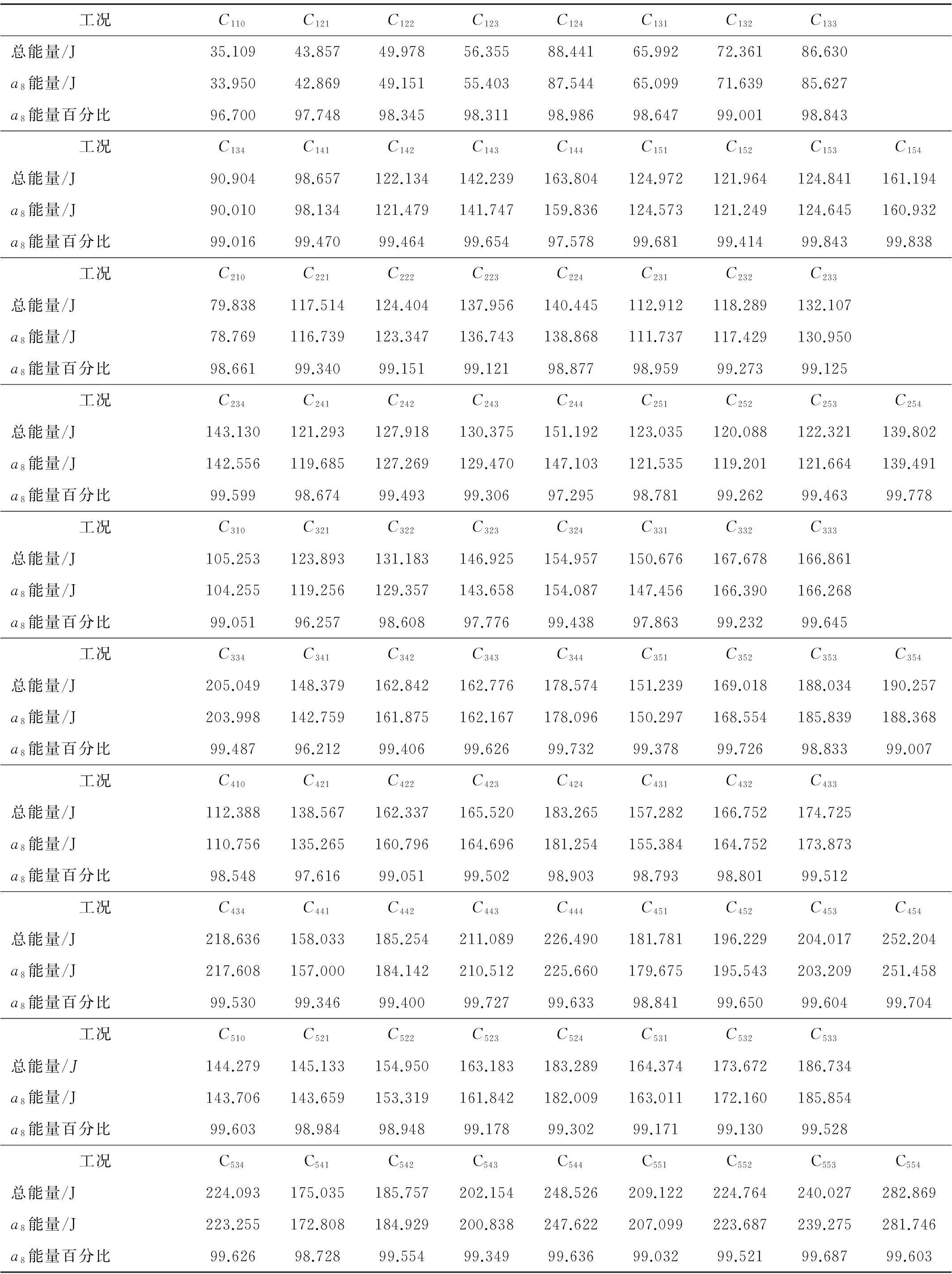
工况C110C121C122C123C124C131C132C133总能量/J35.10943.85749.97856.35588.44165.99272.36186.630a8能量/J33.95042.86949.15155.40387.54465.09971.63985.627a8能量百分比96.70097.74898.34598.31198.98698.64799.00198.843工况C134C141C142C143C144C151C152C153C154总能量/J90.90498.657122.134142.239163.804124.972121.964124.841161.194a8能量/J90.01098.134121.479141.747159.836124.573121.249124.645160.932a8能量百分比99.01699.47099.46499.65497.57899.68199.41499.84399.838工况C210C221C222C223C224C231C232C233总能量/J79.838117.514124.404137.956140.445112.912118.289132.107a8能量/J78.769116.739123.347136.743138.868111.737117.429130.950a8能量百分比98.66199.34099.15199.12198.87798.95999.27399.125工况C234C241C242C243C244C251C252C253C254总能量/J143.130121.293127.918130.375151.192123.035120.088122.321139.802a8能量/J142.556119.685127.269129.470147.103121.535119.201121.664139.491a8能量百分比99.59998.67499.49399.30697.29598.78199.26299.46399.778工况C310C321C322C323C324C331C332C333总能量/J105.253123.893131.183146.925154.957150.676167.678166.861a8能量/J104.255119.256129.357143.658154.087147.456166.390166.268a8能量百分比99.05196.25798.60897.77699.43897.86399.23299.645工况C334C341C342C343C344C351C352C353C354总能量/J205.049148.379162.842162.776178.574151.239169.018188.034190.257a8能量/J203.998142.759161.875162.167178.096150.297168.554185.839188.368a8能量百分比99.48796.21299.40699.62699.73299.37899.72698.83399.007工况C410C421C422C423C424C431C432C433总能量/J112.388138.567162.337165.520183.265157.282166.752174.725a8能量/J110.756135.265160.796164.696181.254155.384164.752173.873a8能量百分比98.54897.61699.05199.50298.90398.79398.80199.512工况C434C441C442C443C444C451C452C453C454总能量/J218.636158.033185.254211.089226.490181.781196.229204.017252.204a8能量/J217.608157.000184.142210.512225.660179.675195.543203.209251.458a8能量百分比99.53099.34699.40099.72799.63398.84199.65099.60499.704工况C510C521C522C523C524C531C532C533总能量/J144.279145.133154.950163.183183.289164.374173.672186.734a8能量/J143.706143.659153.319161.842182.009163.011172.160185.854a8能量百分比99.60398.98498.94899.17899.30299.17199.13099.528工况C534C541C542C543C544C551C552C553C554总能量/J224.093175.035185.757202.154248.526209.122224.764240.027282.869a8能量/J223.255172.808184.929200.838247.622207.099223.687239.275281.746a8能量百分比99.62698.72899.55499.34999.63699.03299.52199.68799.603

据统计结果可得：①泥石流冲击总能量与低频近似系数a8频段内能量几近一致(图5、图6)，据表3数据统计计算，96%以上泥石流冲击能量完全位于<1.958 Hz的低频区间，即逼近真实信号f(t)为较平稳低频有效信号。②泥石流冲击信号总能量随浆体黏度增长而增长，黏度从0 Pa·s(C1rd)增至0.93 Pa·s(C5rd)时同黏度对应的不同固相比与粒径组合的17种工况(r=1，2，…5，d=1，2，…4)总能量为1 649.432 J、2 142.619 J、2 703.595 J、3 094.569 J、3 320.532 J(表3、图5)。③相同浆体黏度下，随固相比增大泥石流冲击总能量增大， 如黏度=0.93 Pa·s(图5中C5线)时，固相比从0增至0.16，4组固相粒径组泥石流冲击能量均值分别为161.638 5 J、187.218 2 J、202.867 9 J、239.195 7 J。④泥石流冲击信号能量随固相颗粒径增大而增大(相同浆体黏度、固相比)，且固体颗粒径达到1.3～1.5 cm时(图3工况4、8、12、16)，泥石流冲击能量增长幅度最明显。⑤泥石流冲击信号在细节系数(d1～d8)频段内的冲击能量波动明显(图6)。黏度较小(0 Pa·s、0.13 Pa·s)时泥石流紊动性强，细节系数频段内冲击能量在大固相比(r=0.08)与大固相颗粒径(d=1.3～1.5 cm)组合工况下(图6工况12)波动明显；而黏度较大为0.72 Pa·s与0.93 Pa·s时细节系数频段内冲击能量无明显峰值，呈平缓均布趋势。

4结论

通过实验获得不同浆体黏度、不同固相比及不同颗粒粒径组合的85组泥石流冲击信号，500余万数据，利用小波分析方法获得泥石流冲击能量特征，结论如下：

(1)泥石流冲击力幅值与冲击荷载频谱能量均集中于低频近似系数a8频段(<1.958 Hz)内，逼近真实泥石流冲击信号，为较平稳的低频有效信号，泥石流冲击信号能量96%以上聚集在0～1.958 Hz频段内。

(2)泥石流冲击信号在近似系数a8频段内的能量分布规律与总冲击能量变化趋势相同，细节系数(d1～d8)频段内的冲击能量波动明显，即近似系数变化能反应泥石流冲击能量在不同材料组合下变化。

(3)通过对浆体黏度、固相比与颗粒粒径组合85组工况的泥石流冲击能量特性及冲击能量随黏度、固相比及颗粒粒径变化趋势探讨，可进一步丰富泥石流动力学知识。能量分布<1.958 Hz特征可为泥石流防治结构与消能结构设计提供理论参考。

参 考 文 献

[1] 陈洪凯,唐红梅,陈野鹰.公路泥石流力学[M].北京:科学出版社,2007.

[2] Iverson R M, Reid M E, LaHusen R G. Debris-flow mobilization from landslides[J].Earth Planet,1997,25:85-138.

[3] 陈洪凯,唐红梅,吴四飞. 泥石流运动能量规律初步研究[J].中国地质灾害与防治学报,2006,15(增刊1):50-55.

CHEN Hong-kai,TANG Hong-mei,WU Si-fei. Primary research on debris flow’s locomotor energy[J]. The Chinese Journal of Geological Hazard and Control, 2006,15(Sup1): 50-55.

[4] 王兆印.泥石流龙头运动的实验研究及能量理论[J]. 水利学报,2001(3):18-26.

WANG Zhao-yin. Experimental study oil debris flow head and the energy theory[J].Journal of Hydraulic Engineering,2001(3):18-26.

[5] 舒安平,张志东,王乐,等.基于能量耗损原理的泥石流分界粒径确定方法[J].水利学报,2008,38(3): 257-263.

SHU An-ping,ZHANG Zhi-dong,WANG Le,et al. Method for determining the critical grain size of viscous debris flow based on energy dissipation principle[J]. Journal of Hydraulic Engineering, 2008,38(3): 257-263.

[6] 曾超.泥石流作用下建筑物易损性评价方法[D]. 北京:中国科学院研究生院,2014.

[7] 冯泽深,高甲荣.基于能量概念的泥石流减灾新思路[J].中国地质灾害与防治学报,2009,20(1): 27-31.

FENG Ze-shen,GAO Jia-rong. A new viewpoint of debris flow disaster mitigation based on energy conception[J].The Chinese Journal of Geological Hazard and Control,2009,20(1):27-31.

[8] 王兆印,漆力健,王旭昭,等. 消能结构防治泥石流研究-以文家沟为例[J].水利学报,2012, 43(3):253-263.

WANG Zhao-yin, QI Li-jian, WANG Xu-zhao,et al. Debris flow control with energy dissipation structures-experiences from Wenjiagou[J]. Journal of Hydraulic Engineering, 2012, 43(3):253-263.

[9] 李万,张志华,陈沧海,等.水下爆炸毁伤水下目标的能量分布特征[J].高压物理学报,2012,26(5): 537-544.

LI Wan,ZHANG Zhi-hua,CHEN Cang-hai,et al. Features of energy distribution of underwater target by underwater explosion[J]. Chinese Journal of High Pressure Physics, 2012,26(5): 537-544.

[10] Zhong Guo-sheng,Ao Li-ping,Zhao Kui. Influence of explosion parameters on wavelet packet frequency band energy distribution of blast vibration[J]. Mining Science and Technology(China),2011,21: 35-40.

[11] 陈洪凯,鲜学福,唐红梅,等.水石流冲击信号能量分布实验研究[J].振动与冲击,2012,31(14): 56-59.

CHEN Hong-kai,XIAN Xue-fu, TANG Hong-mei,et al. Energy distribution in spectrum of shock signal for non-viscous debris flow[J]. Journal of Vibration and Shock, 2012,31(14): 56-59.

[12] 何晓英,唐红梅,朱绣竹,等.泥石流浆体冲击特性实验研究[J].振动与冲击,2013,32(24):127-134.

HE Xiao-ying,TANG Hong-mei,ZHU Xiu-zhu,et al. Tests for impacting characteristics of debris flow slurry[J]. Journal of Vibration and Shock, 2013,32(24):127-134.

[13] Mallat S, Hwang W L. Singularity detection and processing with wavelet[J]. IEEE Trans on Information Theory,1992,38(2):617-643.

Experimental study on the energy distribution characteristics of impacting signals of debris flow considering the slurry viscosity and particle collision

HEXiao-ying,CHENHong-kai,TANGHong-mei

(Institute of Geotechnical Engineering,Chongqing Jiaotong University, Chongqing 400074, China)

Abstract:A physical experimental model in laboratory was established for debris flow, and 85 groups’ conditions were implemented considering the combination of five slurry viscosities, five solid phase ratios and four grain diameters. The impacting force signals of debris flow under the experimental conditions were denoised and disposed in time-frequency domain by wavelet method, then the impacting signals were broken down to nine frequency ranges (0～1.958 Hz, 1.958～3.906 Hz, 3.906～7.812 Hz, 7.812～15.625 Hz, 15.625～31.25 Hz, 31.25～62.5 Hz, 62.5～125 Hz, 125～250 Hz, 250～500 Hz) and the energy distribution characteristics in each frequency range were calculated. The results show that, generally, the impacting energy of debris flow increases with the increase of slurry viscosity, solid phase ratio and grain diameter, and more than 96 percentages of the energy gets together in the 0～1.958Hz (a8) low frequency range. The result is positive in the studies on dynamical features of debris flow.

Key words:impacting force of debris flow; distribution characteristics of energy; model test; slurry viscosity; solid phase grain

中图分类号:P642.23；O359

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.011

收稿日期：2015-01-07修改稿收到日期：2015-04-01

基金项目：国家自然科学基金(41071017)；2013重庆高校创新团队建设计划资助项目(KJTD201305);重庆市教委科学技术研究项目(KJ1500503)；重庆市科委重点自然基金项目(CSTC2013JJB30001)

第一作者 何晓英 女，博士后，讲师，1987年4月生