基于萤火虫算法的PID参数优化方法研究

陈路伟

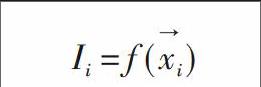
摘 要： 针对传统的PID参数整定方法越来越费时且难以满足控制要求的问题，提出一种采用萤火虫算法来优化PID控制参数的方法，设计了基于Simulink的参数优化模型，并进行仿真计算。结果表明，利用萤火虫算法优化PID控制器参数的阶跃响应响应时间短，基本没有超调，跟踪过程较平稳，仿真结果证明将萤火虫算法应用于PID参数优化是切实可行的。

关键词： PID； 萤火虫算法； 参数优化； Simulink

中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）18?0005?03

Abstract： Since the traditional PID parameter tuning method has become more and more time?consuming， and is hard to meet the control requirements， a new method of optimizing PID control parameters by using firefly algorithm is proposed in this paper， and a parameters optimization model based on Simulink was designed to carry out the simulation calculation. The results show that PID controller parameters optimized with the firefly algorithm has short step response time and stable tracking process， and proves that it is feasible to adopt the firefly algorithm in PID parameter optimization.

Keywords： PID； firefly algorithm； parameter optimization； Simulink

PID控制是比例微分积分控制的简称。在生产过程控制的发展历程中，PID控制是历史最悠久、生命力最顽强，并且也是目前为止应用最多的控制方法[1]。PID控制的精确程度主要取决于其[KP，KI，KD]三个控制参数，但这三个参数的参数整定复杂繁琐。过去人们往往使用经验规则加试凑的方式来调整PID控制参数，但随着控制工程的快速发展，这种方法越来越费时且难以满足控制要求。为解决这种情况，采用智能优化算法来优化PID控制参数应运而生，并取得了明显的效果。文献[2]研究了采用蚁群算法优化PID控制器参数；文献[3]研究了使用遗传算法优化PID参数的方法；文献[4]在基础上改进了用于优化的遗传算法，提出了基于自适应遗传算法的PID参数整定方法；文献[5]采用改进的粒子群算法对PID参数进行了整定，均取得了一定的成果。在本文中研究采用一种全新的智能算法——萤火虫算法对PID参数进行整定，研究其在PID参数整定的可行性及其效果。

1 萤火虫算法

萤火虫算法（GSO）是群集智能优化算法领域的最新算法，它是由印度学者Krishnan和Ghose提出的一种群智能随机优化算法[6]。该算法从仿生学角度出发，模拟自然界中的萤火虫发光特性，通过荧光素值大小相互吸引对方，达到彼此交流信息的目的。实验表明，萤火虫算法在寻找各种全局最优解方面比遗传算法等更有效，成功率更高[7]。

萤火虫算法的核心思想是被绝对亮度比他大的萤火虫吸引，并根据位置更新公式更新自身位置。具体算法步骤为[8]：

首先建立萤火虫的绝对亮度和目标函数的关系，用萤火虫的绝对亮度表征萤火虫所在位置处潜在解的目标函数值，即：

[Ii=f（xi→）]

假设萤火虫i的绝对亮度大于萤火虫j的绝对亮度，那么认为萤火虫j被萤火虫i吸引而向其移动，这种吸引力的大小与由两者之间的相对亮度成正比，考虑到萤火虫i的亮度随着距离的增加以及空气的吸收而减弱，定义两者之间的相对亮度为：

[Iij（rij）=Iie-γr2ij]

式中：[rij]为两萤火虫之间的距离；[γ]为光吸收系数。

那么萤火虫i对萤火虫j的吸引力为：

[βij（rij）=β0e-γr2ij]

式中[β0]为最大吸引力。

萤火虫j的位置更新公式为：

[xi→（t+1）=xj→（t）+βij（rij）（xi→（t）-xj→（t））+αεj→]

式中：[t]为算法的迭代次数；[α]为常数；[εj→]为随机数向量。

综上所述，萤火虫算法的基本流程可以用图1描述。

2 萤火虫算法优化PID控制器参数步骤

2.1 问题描述

PID控制器系统结构图如图2所示。

PID控制器的优化问题就是确定一组合适的参数[KP，KI，KD]，使得指标达到最优。

为了获得满意的过渡过程动态特性，采用误差绝对值时间积分作为待优化的最小目标函数，为了防止控制能量过大，在目标函数中加入控制输入的平方项[9]：

[J=0∞（w1e（t）+w2u2（t））dt+w3t] （1）

式中：[e（t）]为系统误差；[u（t）]为控制器输入；[w]为权值。

选取的被控对象为式（2）：

[G（s）=s+2s4+8s3+4s2-s+0.4] （2）

建立的优化模型如图3所示。

图3中输出端口1即为式（2）所示指标，通过将时间及误差绝对值进行积分后得到。

2.2 优化设计过程

优化过程如图4所示。

如图4所示，萤火虫优化算法与Simulink之间连接的纽带是萤火虫（即PID控制器参数）和其对应的适应值（即控制系统的性能指标）。

首先产生初始化的萤火虫种群（即控制其参数的初始值）依次赋给PID控制器参数，然后运行控制系统模型，得到相应的性能指标，传递给优化算法作为其适应度值，最后判断优化是否结束。

2.3 仿真

设置萤火虫算法仿真参数如下所述，萤火虫数目为40，最大迭代次数为100， 最大吸引力[β0=1.0]，光吸收系数[γ=1.0]。优化后得到的性能指标和控制器参数为：[KP=16.129，KI=0.220 9，KD=0.220 9，ITAE=][24.981 2]。

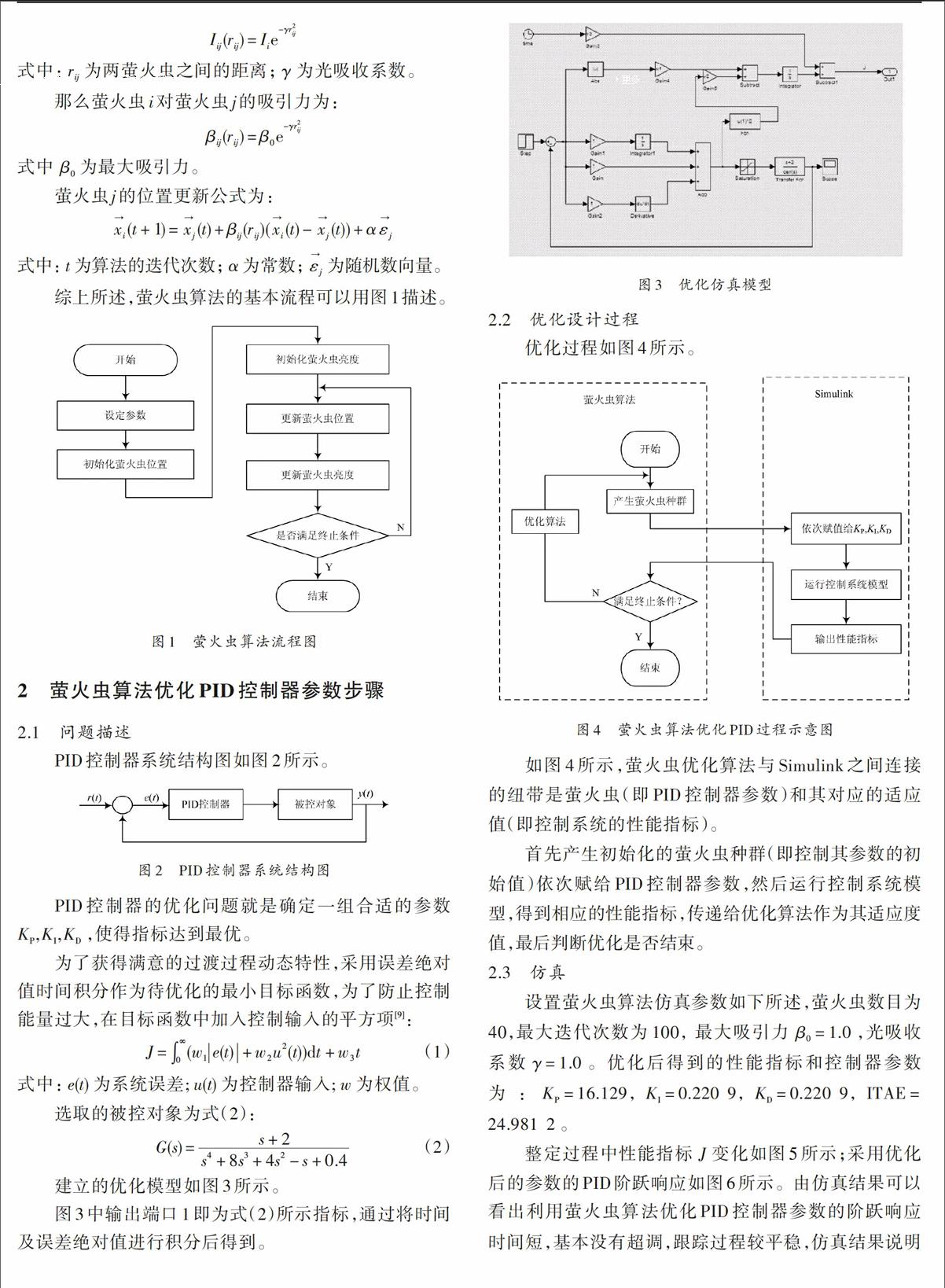
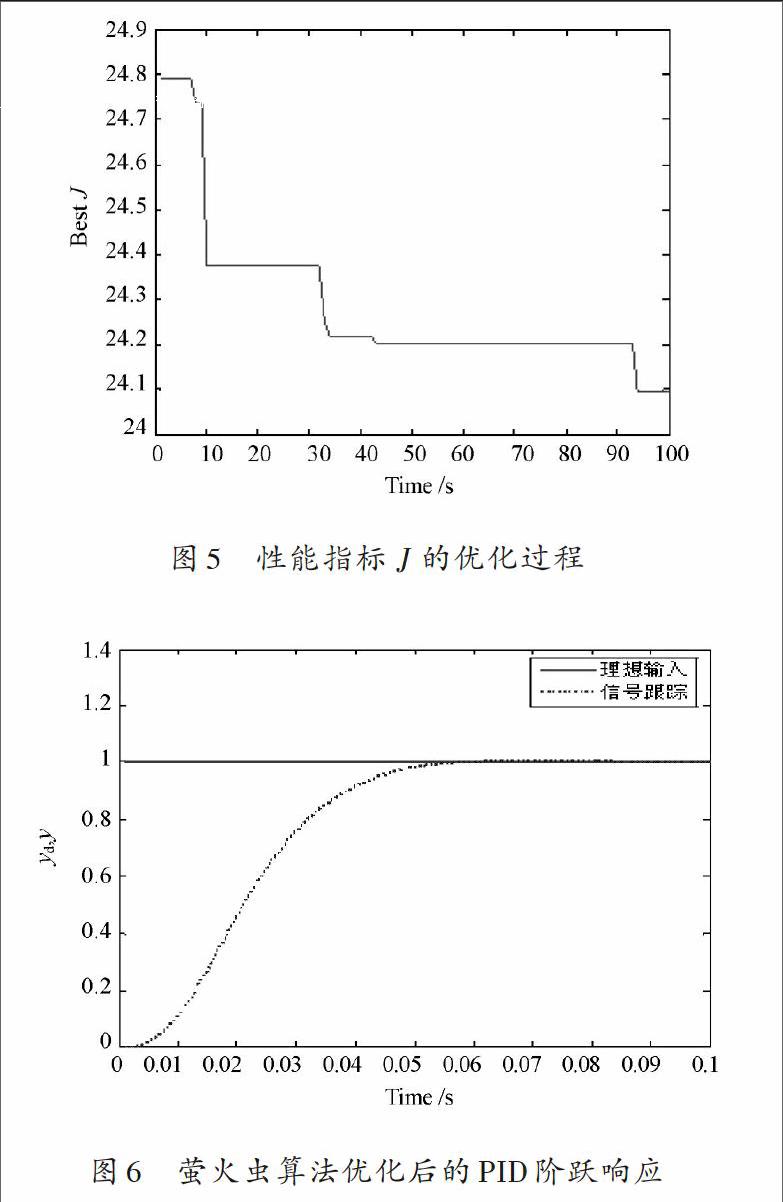
整定过程中性能指标[J]变化如图5所示；采用优化后的参数的PID阶跃响应如图6所示。由仿真结果可以看出利用萤火虫算法优化PID控制器参数的阶跃响应时间短，基本没有超调，跟踪过程较平稳，仿真结果说明采用萤火虫算法优化PID控制器参数是确实可行的。

3 结 论

本文改进了传统的PID参数优化方法，提出采用萤火虫算法的参数优化方法，利用Simnulink构建了基于萤火虫算法的PID参数优化仿真模型，并针对算例进行了仿真计算。结果表明，该算法实现简单寻优快速并具有较高的全局收敛能力。阶跃响应时间短，基本没有超调，跟踪过程较平稳，可以说采用萤火虫算法优化PID控制器参数是确实可行的。

参考文献

[1] 刘金琨.先进PID控制MATLAB仿真[M].北京：清华大学出版社，2005.

[2] 段海滨，王道波，黄向华，等.基于蚁群算法的PID参数优化[J].武汉大学学报：工学版，2004，37（5）：97?100.

[3] 毛敏，于希宁.基于遗传算法的PID参数优化[J].中国电力，2002，20（3）：48?51.

[4] 陈丹，方康玲，陈乔礼.遗传算法在PID参数优化中的应用[J].微计算机信息，2007（7）：55?59.

[5] 张娜，李祥崇.改进粒子群算法在PID参数优化中的应用[J].沈阳工程学院学报，2011，7（3）：263?267.

[6] 刘长平，叶春明.一种新颖的仿生群智能优化算法：萤火虫算法[J].计算机应用研究，2011，28（9）：95?97.

[7] 彭喜元，彭宇，戴毓丰.群智能理论及应用[J].电子学报，2003，31（z1）：1982?1988.

[8] 刘鹏，刘弘，郑向伟，等.基于改进萤火虫算法的动态自动聚集路径规划方法[J].计算机应用研究，2011，28（11）：46?49.

[9] 史峰.Matlab智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011.