悬索桥吊杆风致内共振及减振措施初探*1
2016-04-25张志田吴肖波葛耀君陈政清
张志田,吴肖波,葛耀君,陈政清
(1.湖南大学 风工程试验研究中心,湖南 长沙 410082;2.同济大学 土木工程防灾国家重点实验室,上海 200092)
悬索桥吊杆风致内共振及减振措施初探*1
张志田1†,吴肖波1,葛耀君2,陈政清1
(1.湖南大学 风工程试验研究中心,湖南 长沙410082;2.同济大学 土木工程防灾国家重点实验室,上海200092)
摘要:基于现场观测,对特大跨度悬索桥吊杆风致振动现象进行了定性分析,排除了尾流驰振、涡激共振以及风雨激振的可能性.通过数值模拟和理论分析,表明这是一种主缆抖振引起的吊杆共振现象.随机风场激起主缆的随机抖振,而主缆的抖振含有丰富的模态成份,当吊杆的自振频率与具有一定抖振能量的主缆模态的频率充分接近时会激发吊杆的共振.因此,从来流紊流风场中获得能量的是主缆而非吊杆自身.由于与主缆的模态质量相比,一根或几根吊杆的模态质量很小,因此吊杆大幅振动吸收的能量并不会对主缆的振动带来实质性的影响,从而可形成一个相对稳定的能量供给机制.此外,在主缆上加设TMD抑制主缆在吊杆自然频率附近的振动,对吊杆风振有明显的抑制效果.
关键词:悬索桥;吊杆;主缆;抖振;共振;调质阻尼器
拉索体系桥梁是风敏感结构,其主要构件易发生各类风致振动.除加劲梁易发生的颤振以及涡激共振现象外,拉索以及吊杆的风致振动也是极易出现的问题.在桥梁缆索的风振方面,国内外的研究大多围绕在较易发生振动的斜拉索展开,原因是倾斜的拉索容易发生风雨激振及参数共振等振动现象[1-2].而关于竖直安装的圆形吊杆却仅限于单根索的涡激振动和多根并列索的尾流驰振问题[3-5].2012年8月,台风“海葵”登入我国东海岸,引起国内某特大跨悬索桥吊杆的大幅振动.如图1所示,该大桥管理部门的视频资料显示了吊杆的振动强度.部分重要特征总结如下:1)桥塔附近的长吊杆振动激烈,短吊杆振动不明显;2)对于大幅振动的吊杆,其4根平行的钢丝绳振动步调基本一致,但并不完全同步;3)振动方向基本上垂直于桥轴线;4)吊杆振动主频约为0.4 Hz.
类似的振动并非首次出现.1998年春,主跨为1 624 m的丹麦大带东桥尚在施工尾期就发现了吊杆的大幅振动现象.之后,该桥吊杆的大幅振动现象时有发生,且主要发生在长度超过100 m的吊杆[6].十几年来,该桥在吊杆上先后安装了螺旋线、抗风索、调液阻尼器、液压阻尼器等措施但仍然难以控制且无法消除.遗憾的是,至今为止工程师们仍然没有找到该桥吊杆振动的本质原因.在此背景下,本文结合国内某超大跨度悬索桥现场观察到的吊杆振动现象,从理论上讨论了长吊杆的一种新的振动形式,即主缆抖振引起的吊杆内共振,并提出在主缆上加设TMD间接抑制吊杆振动的减振措施.

图1 吊杆的大幅振动
1定性分析
1.1尾流驰振
如图2(a)所示,尾流驰振的机理是由于存在某一特定的平均剪切风场,在该风场中按椭圆形路径振动的圆柱体在一个完整的振动周期内会从风场中吸收能量[7].如果从风场中获得的能量大于结构阻尼的耗散量,振幅将不断增加直到能量平衡,并保持一个稳态的极限环[8].

(a) 平均剪切风场作用

(b) 非定常脉动风场作用
本文所分析的桥梁其吊杆由4根平行排列的钢丝绳组成,因而后面形成的平均剪切风场相对于图2(a)而言更为复杂,如图3所示.但其基本原理完全一致,因而能够根据以下尾流驰振的两个基本特性将这一原因排除.
1)尾流驰振的临界条件实质上是取决于平均剪切风场中拉索的气动力空间分布特性,而与拉索本身的频率特性无关.如图4所示,下游柱体的刚度矩阵可表示为:
(1)
尾流驰振的临界条件由以下不等式确定[9-10]:
(2)
其中:
(3)
(4)
式中:a为质量线密度,其值为常量且与柱体长度无关;CD,CL分别为下游柱体的阻力系数和升力系数;x和z分别为顺风向及横风向无量纲坐标:

(5)

(6)
由式(6)可知,尾流驰振的临界条件实际上是由钢丝绳的准定常空间气动力特性确定而与吊杆的频率特性无关.因而,在假设各吊杆的结构阻尼基本一致的前提下,尾流驰振特性并不随吊杆的长度而变化.然而,现场观测显示仅几根长吊杆发生剧烈振动.

图3 单根吊杆4根平行钢丝绳

图4 下游柱体的尾流驰振模型
2)对于尾流驰振,振动仅限于下游位于尾流区的柱体,而非两者同时发生.然而,现场观测显示上游和下游的钢丝绳均发生振动.
考虑到观察到的振动与上述尾流驰振基本特性不符,故可排除这种振动机理.
1.2涡激共振
对于位于上游其它钢丝绳尾流中的索,不仅只有平均风荷载作用,而且还有非定常脉动气动荷载,如图2(b)所示.下游吊杆的脉动荷载由其自身产生的涡脱及上游杆的尾涡共同控制.在工程常见的雷诺数范围内,柱体的斯托哈数范围为:
St=fd/U=0.2~0.4
(7)
式中:f为柱体漩涡脱落的频率.
不管漩涡脱落是规则还是不规则(谐波或随机),涡脱的卓越频率不应与式(7)确定的范围相差太大.因此,由风速和吊杆直径可得到:
f=St×U/d≈50~100Hz
(8)
很明显该频率范围与观察到的振动临近频率(0.4 Hz)相差太远,故观测到的振动现象不可能是涡激共振.
1.3风雨激振
斜拉索的风雨激振已在国内外范围进行了广泛的研究,虽然台风“海葵”攻击该桥时正在下雨,但是缺少拉索风雨振的基本条件,一是吊杆非倾斜而是竖直安装,其次钢丝绳呈螺旋形且其表面非常粗糙.水线是风雨激振形成的必不可少的条件,但在这种情况下无法形成,故风雨激振的可能性可以排除.
1.4 桥塔尾流引发振动
由于悬索桥长吊杆分布在桥塔附近,人们自然会问是否是桥塔尾流的影响导致吊杆的振动.然而,根据桥塔的尾流特性可排除这一可能性.如图5,首先,从图中可知实际上吊杆距尾流区很远,尤其是当风向垂直于桥轴线时(实际观察的风向近似垂直于桥轴线);其次,不管是哪个风向,桥塔尾流的影响不可能涉及到图5中的4个区域,这与现场观察到的多区域吊杆振动相矛盾.因此,桥塔尾流的气动影响不可能是该桥吊杆振动的实质性原因.

图5 桥塔附近的吊杆布置(单位:m)
1.5抖振引起的共振
根据大桥管理部门拍摄的视频,台风“海葵”作用时,桥上几乎没有车辆,因此,车辆激起的振动也可排除.最后唯一可以肯定的是,吊杆的振动必然是来源于风的作用,直接或者间接.
风场和作用在结构上的风荷载都是随机的,因此结构响应也是随机的.此外,无论是风场还是脉动风荷载都具有广谱特性.因此,全桥会有广谱特性的抖振响应.主缆具有丰富的横向振动自然模态,所有吊杆上端都与主缆相连,不难推测,主缆的振动很可能是吊杆的激励源.吊杆的自然频率随着安装长度逐渐改变,当吊杆的频率与主缆的某阶具有一定抖振能量的模态的频率充分接近时,能激发其共振.以下将通过数值计算方法验证这种共振机制.
2有限元模型与荷载
2.1有限元模型
该桥总跨径2 713 m,主跨长度1 650 m,北边跨长度578 m,主跨和北边跨为连续钢箱梁并有吊杆支撑.南边是总长为485 m的引桥.大桥整体及吊杆布置如图6所示,有限元模型如图7所示.
由于要调查吊杆的振动问题,因此在全桥有限元模型中吊杆需要进行细化以体现其振动特性.另一方面,从现场观测的结果来看,短吊杆并没有发生大幅振动现象.因此,基于节省计算资源考虑,吊杆单元的细化只限定在桥塔附近的10根长吊杆(主跨5根:M1~M5;边跨5根:S1~S5),如图8所示,每根吊杆被细化为12个单元,足以模拟从低到中等频率的模态振动.
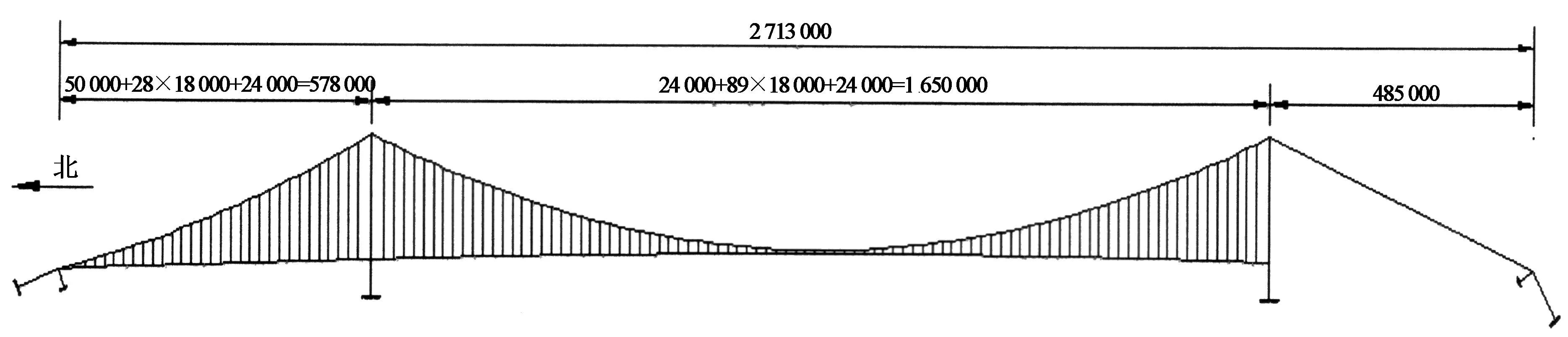
图6 吊杆布置图(单位:mm)

图7 大桥有限元模型
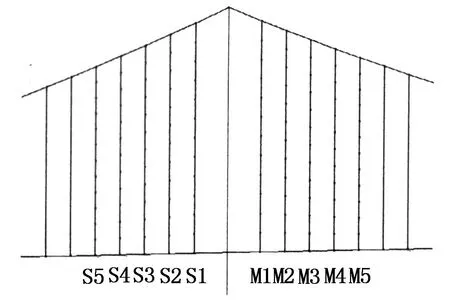
图8 吊杆单元细化
结构的基本动力特性可以从结构的有限元模型特征值分析得到,由于吊杆的自振模态分布太多太广,这里仅在图9给出S2和M2号等长吊杆的部分横向振动模态.
从图9可知吊杆的自振频率较低且分布紧密,比如第29阶(f29=0.371 5 Hz)和第39阶(f39=0.398 5 Hz),阶次相差大但振动形态与频率却非常接近.且在很小的频率区间内会出现大量吊杆和主缆同时的振动模态.
需要指出的是:虽然S2和M2号吊杆短于S1和M1号吊杆,但其固有频率明显低于S1和M1号吊杆.究其原因是S1,S2,M1和M2号吊杆的钢丝绳面积均为3 960 mm2,远大于其他吊杆的标准面积1 815 mm2,而在S1和M1号吊杆之间的主梁在竖向没有受到支座的竖向支撑,此处局部跨度为48 m,远大于其他两根临近吊杆间的标准跨度18 m,成桥状态S1和M1吊杆的轴向拉力约为S2号和M2号吊杆的2倍.
因此,由张拉弦固有频率计算公式:
(9)
式中:f为固有频率;n为模态阶数;L为弦长度;T为弦内部张力;ρ为弦线密度.
故S2号和M2号吊杆一阶固有频率更低,同时说明对于柔性结构的该超大跨悬索桥,S2号和M2号吊杆较其他吊杆更容易引起振动,现场观测也显示S2和M2号吊杆的振动最激烈.相比于安装在两固定点间张拉弦的一阶自然频率是个常数,从图9可以看出该悬索桥上弹性安装的吊杆自振频率是可变的,主要依赖于主缆特定的振动形态.

图9 S2和M2号吊杆部分自然模态
2.2抖振风荷载
由于吊杆长度和断面尺寸较小,故忽略其本身所受的脉动风荷载.数值模拟采用时域分析法,加劲梁施加阻力、升力和升力矩;主缆荷载只施加阻力.作用在单位长度主梁上抖振风荷载表达式如下:
(10)

(11)
(12)


图10 主梁横截面(单位:mm)

攻角/(°)
作用在单位长度主缆上的瞬时风荷载可表示为:
(13)

将瞬时风荷载沿平均风方向进行分解并减去平均值后得其脉动风荷载的水平分量:
(14)
垂直于平均风向及主缆轴向的脉动风荷载分量则为:
(15)
其中α角定义为:
(16)
3数值模拟
本文数值模拟的目的不是为了定量重现台风“海葵”登陆时的大桥结构响应,而是为了探讨该桥长吊杆的风致振动机理,找出其风振的主要原因.因此,同时提取吊杆的中点、与主缆连接的上端点以及与主梁连接的下端点的横向位移时程进行讨论;同时对振动进行频谱分析,找到能量传递途径.
3.1阻尼比选取
采用Rayleigh阻尼模型,瑞利阻尼矩阵[C]由质量矩阵[M]和刚度矩阵[K]按比例组合构造而成的,公式如下:

(17)
式中:α,β为瑞利阻尼系数.对于特定模态固有圆频率ωi,对应的阻尼比ξi为:
(18)
根据模态分析结果,选取主缆横向振动主频0.227 8 Hz为第一频率参考点,这一频率点对应的阻尼比为0.005;选取S2号吊杆自然频率0.371 5 Hz为第二频率参考点,该频率点对应的阻尼比为0.003,阻尼曲线如图12所示.
3.2 数值模拟结果
时域数值分析过程中,仅在主梁和主缆上施加抖振风荷载,吊杆本身上并不施加荷载.
3.2.1 吊杆横向位移时程
主梁主跨中点桥面标高的平均风速取为U=30 m/s时,经过动力时程分析,得到S1~S5和M1~M5号吊杆中点和与主缆连接上端点的横向振动位移时程,如图13所示.

频率/Hz
由时程分析结果可知,部分吊杆具有明显的共振特征,尤其是S2与M2号吊杆.主缆对吊杆只需较小幅度的激励就可以导致吊杆相当大的横向振动.从图中可以看出,大多数其他吊杆仍表现出典型的强迫振动特征.需要指出的是,为避免在定性时造成困惑,本文忽略作用在吊杆上的风荷载,因而吊杆振动的激励源只可能来自与主缆连接的上端点或者与主梁连接的下端点.然而,本桥加劲梁的低阶横向振动固有频率与吊杆振动主频率相差甚远.因此,可确定激励源只能来自主缆的振动.
需要强调的是,本文是从定性的角度去探讨这一种风致共振现象,而非定量.这主要体现在以下两方面:首先,在数值分析过程中使用的脉动风谱特性、空间相关特性是模拟所得,不能也不可能与任一座桥梁的实际脉动风的风谱特性及相关特性完全一致.这些差异必定会造成结构随机响应的计算特性与实际之间的差异,因此风速的大小无法定量地确定结构的响应,尤其是某一频率点处的谱值;其次,有限元模型所确定的动力特性,如频率与阻尼,并没有与该桥的实际情况进行校核.有限元建模过程中,主缆以及吊杆中的初始张力是以与结构自重荷载基本平衡的原则进行确定的.但在实桥上,受施工过程等多方面因素的影响,吊杆的张力可能会与计算模型有所出入.甚至一组吊杆的4根钢丝绳的张力都有可能不是完全一样.因此,实际桥梁上哪些吊杆最容易出现共振现象,共振幅值会有多大,这些都不能由数值分析来精确定位.本文数值分析说明的基本原理是,只要主缆与吊杆的自振频率足够接近,且风场在这一频率附近处能激起主缆足够的抖振能量,那么主缆与吊杆之间的内共振现象就一定会发生.在大跨度悬索桥中,由于吊杆长度的变化规律,满足这一条件并不困难.

图13 吊杆中点和与上端点横向位移时程(U=30 m/s)
3.2.2 频谱分析
为了进一步定性分析吊杆的共振问题,取振动最为激烈的长吊杆(S2号吊杆)横向位移时程进行频谱分析,如图14所示.从图14频谱结果可以看出吊杆共振仅需很小幅度的主缆激励.频谱结果表明主缆横向振动的卓越频率为0.22 Hz,并非吊杆的共振频率0.37 Hz,但我们可注意到在0.37 Hz附近,主缆有很小的一个能量峰值点,正是这一部分频率特性的能量激起了吊杆共振响应,导致主缆从脉动风场中吸收的动能转化为吊杆的动能.另一方面,我们可以注意到加劲梁在吊杆共振频率(0.37 Hz)附近几乎没有可察觉的能量.值得讨论的是,在内共振中,通常能量存在一个此消彼长的关系,即当能量从某一构件转移到另一构件后,前者振幅会减小.然而,本文研究的共振机制在主缆与吊杆之间发生,前者的模态质量远远大于后者,因此吊杆从主缆吸收能量并不一定会对主缆本身的振动造成实质性的影响,从而可形成一个稳定的能量供给机制.换言之,主缆自身的振幅基本上只受随机风场的强迫振动控制,跟转移到吊杆上去的那一小部分能量关系不大.由于随机性是抖振的固有特性,因此这种主缆抖振引起的吊杆共振也势必同样具有随机特性,这一性质从时间上表现为不平稳,这一点从图13可以明显地观察到.

图14 S2号吊杆横向位移振幅频谱(U=30 m/s)
4 减振措施初探
吊杆的持续大幅振动可能在短时间内造成索股疲劳和腐蚀,也会引起行人或行车的不舒适感和人们对桥梁使用安全性的怀疑,因此应采取相应的措施控制吊杆的振动.抑制吊杆风振的措施很多,多是从吊杆自身出发,比如在拉索之间增设附加拉索,改变拉索表面形状从而改变其空气动力特性,增设被动、主动或半主动阻尼器等.由于本文研究的拉索共振其能量源于主缆,上述控制措施效果不佳,故在主缆上加设调谐质量阻尼器,通过抑制主缆在吊杆共振频率附近的振动间接抑制吊杆的振动,从理论上讨论其对吊杆振动的控制效果.
由图14(a)可知,S2号吊杆在其共振频率附近(0.350~0.375 Hz间)振动剧烈且峰值密集,为了改善TMD的有效性和鲁棒性,采用多个具有不同动力特性组成且频率呈线性分布的TMD抑制主缆在该频率区间的振动.为使减振效果最优,应对TMD的各项参数(频率比、质量比、阻尼比和安装位置等)进行最优化设计[11].TMD的控制频率f和阻尼常数C分别为:
(19)
式中:ξ为阻尼比.
本文的TMD参数并没有在全局范围内进行优化设计,仅取一组参数进行定性分析以观其效果.主缆上TMD布置如下:TMD安装在S1~S5和M1~M5号吊杆与主缆连接的上端点,共10个TMD.以S1~S5号吊杆上端点安装的TMD为例,每个TMD的控制频率为吊杆横向位移频谱峰值由大到小排列(依次为0.126 96 m,0.078 55 m,0.059 03 m,0.047 16 m,0.043 82 m)对应的频率(依次为0.371 11 Hz,0.361 11 Hz,0.362 22 Hz,0.364 44 Hz和0.360 00 Hz).经由多组参数优化计算,取一组控制效果最明显,刚度K=100 kN/m保持不变,离散TMD的质量M(依次为183 92 kg,194 25 kg,193 06 kg,190 71 kg,195 45 kg),阻尼比ξ=8.0%保持不变.
在主缆上加设TMD与未加设TMD的横向位移时程比较如图15所示,可知吊杆减振效果明显并达到80%以上.频谱分析结果如图16所示,主缆上加设TMD后其在吊杆共振频率附近振动幅值明显降低,吊杆中点的共振甚至低于其在主缆横向振动主频(0.22 Hz)处其随主缆的振动,可见减振效果非常明显.从理论上来说,控制主缆的振动并不改变吊杆本身与主缆的内共振特性,但由于主缆是吊杆振动的能量供给源,因此控制主缆的振动相当于降低了从主缆至吊杆的能量供给,从而间接地控制了吊杆的共振幅值.

图15 S2吊杆横向位移时程(U=30 m/s,TMD)

图16 S2号吊杆横向位移振幅频谱(U=30 m/s,TMD)
5结论
基于本文的理论分析和数值模拟可以得出以下结论:
1)分析结果表明,大跨度悬索桥主缆与吊杆存在一种因抖振引起的内共振机制.当主缆横向振动频率与吊杆的自振频率充分接近时能引发这种共振现象.由于主缆的模态质量远远大于某一根或几根吊杆的模态质量,因此吊杆从主缆吸收能量并不会造成主缆振幅的明显衰减,从而形成一个稳定的能量供给机制.
2)抖振是在所有风速范围内均存在的风振现象.对于某一座悬索桥而言,一旦存在本文指出的这一类共振机制,那么它存在的风速以及风向范围必定相当广泛.
3)在主缆上加设TMD可间接控制吊杆的振动,且减振效果明显.对于该类振动现象,该措施将来可作为一种供实际工程参考的减振措施.
参考文献
[1]COSTA A P, MARTINS J A C, BRANCO F,etal. Oscillations of bridge stay cables induced by periodic motions of deck and/or towers [J]. Journal of Engineering Methanics, 1996,122(7):613-622.
[2]ROYER-CARFAGNI G F. Parametric-resonance-induced cable vibrations in network cable-stayed bridges, a continuum approach [J]. Journal of Sound and Vibration, 2003, 262(5):1191-1222.
[3]CIGADA A, DIANA G, FALCO M,etal. Vortex shedding and wake-induced vibrations in single and bundle cables [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72(11):253-263.
[4]WILLIAMS R G, SUARIS W. An analytical approach to wake interference effects on circular cylindrical structures [J]. Journal of Sound and Vibration, 2006, 295(1):266-281.
[5]ZDRAVKOVICH M M. Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 28(1):183-200.
[6]LAURSEN Ernst, BITSCH Niels, ANDERSEN Jacob E. Analysis and mitigation of large amplitude cable vibrations at the great belt east bridge[C]//Proc 32thCongress IABSE.Copenhagen, 2006:64-71.
[7]BOKAIAN A. Galloping of a circular cylinder in the wake of another [J]. Journal of Sound and Vibration, 1989,128(1):71-85.
[8]DOWELL E H, CLARK R,COX D,etal. A modern course in aeroelasticity [M]. Fourth Revised and Enlarged Edition. Dordrecht:Kluwer Academic Publishers, 2004: 314-327.
[10]PRICE S J. Wake induced flutter of power transmission conductors [J]. Journal of Sound and Vibration, 1975, 38(1):125-147.
[11]GU M, CHEN S R, CHANG C C. Parametric study on multiple tuned mass dampers for buffeting control of Yangpu Bridge [J]. J Wind Engineering and Industrial Aerodynamics, 2001,89(11/12): 987-1000.
Wind Induced Internal Resonance and the Control Method of Suspension Bridge Hangers
ZHANG Zhi-tian1†, WU Xiao-bo1, GE Yao-jun2, CHEN Zheng-qing1
(1. Wind Engineering Experiment Research Center, Hunan Univ, Changsha,Hunan410082, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji Univ, Shanghai200092, China)
Abstract:The mechanism of wind-induced oscillation of hangers in a long-span suspension bridge was investigated qualitatively on the basis of field observations, and the possibility of wake galloping, or vortex-induced resonance, or wind-rain-induced oscillation was excluded by reasoning. Numerical simulation and theoretical analysis reveal that this is a kind of resonance induced by the buffeting of main cables. Stochastic wind fields excite the stochastic responses of the main cables, which are abundant in a wide range of modal components, and the resonance occurs when the natural frequency of a hanger is adequately close to one of the main cable’s natural frequencies that possess enough energy. Hence, it is not the hangers themselves but the main cables that are responsible for the energy absorbing from the turbulence. Compared with the modal mass of a main cable, the mass of one hanger is too small to pose substantial effects on the oscillation of the main cable, and therefore, a steady supply of energy from the main cable to the hangers can be formed. Furthermore, TMD mounted on the main cables can suppress the wind-induced vibration of cables at the natural frequency of hangers, which results in the significant reduction of the vibration of the hangers.
Key words:suspension bridge; hanger; main cable; buffeting; resonance; tuned mass damper
中图分类号:U448.25
文献标识码:A
作者简介:张志田(1974-),男,湖南新化人,湖南大学教授,博士†通讯联系人,E-mail: zhangzhitian@hnu.edu.cn
*收稿日期:2015-02-04基金项目:国家自然科学基金资助项目(51178182,51578233), National Natural Science Foundation of China (51178182,51578233)
文章编号:1674-2974(2016)01-0011-09
