大跨度悬索桥吊索减振技术研究与应用*1
2016-04-25陈政清华旭刚李寿英颜永先牛华伟
陈政清, 雷 旭,华旭刚,李寿英,颜永先,温 青,牛华伟
(1.湖南大学 风工程试验研究中心,湖南 长沙 410082;2.浙江省交通投资集团有限公司,浙江 杭州 310014)
大跨度悬索桥吊索减振技术研究与应用*1
陈政清1†, 雷旭1,华旭刚1,李寿英1,颜永先2,温青1,牛华伟1
(1.湖南大学 风工程试验研究中心,湖南 长沙410082;2.浙江省交通投资集团有限公司,浙江 杭州310014)
摘要:针对大跨度悬索桥吊索频率低、阻尼小、以致容易发生风振的弱点,以舟山西堠门大桥的长细吊索风振问题为工程背景,研究了其抗风减振方法.首先通过环境激励法确定了吊索的动力特性.然后基于理论分析和风洞试验确定了分隔器减振方案,并对不同分隔器数量时的减振效果进行了对比研究.最后通过某大风天气下有无分隔器的两组吊索的实测数据结果对比验证了分隔器减振方案的有效性.试验和实测结果表明:安装分隔器后吊索的碰索现象不再发生,吊索的各阶振动均明显减小,各阶减振率达55%~95%.
关键词:大跨度悬索桥;吊索;风致影响;分隔器;完全气弹模型;现场实测
随着大跨度悬索桥的兴建,其细长吊索的风致振动问题已成为决定其使用寿命和行车安全的关键性问题,特别是在沿海或山区峡谷地区大风下的多索股吊索振动将会引起邻近索股之间的碰撞和桥面振动,极大地影响桥梁安全.
对于诸如吊索之类的细长构件风致振动控制的问题,国内外学者已有大量研究,目前主要有气动措施、结构措施和机械阻尼措施3大类控制方法[1-2].气动措施适用于已知振动机理的单因素吊(拉)索振动控制,譬如预防拉索风雨振时在索表面打凹坑以及缠绕螺旋线方式等[3],但对于不清楚振动机理和多因素耦合下的风致振动效果并不明显.机械阻尼措施是通过给阻尼很小的吊(拉)索结构附加阻尼来提高其抗风稳定性,包括附加减振锤[4]、调谐质量阻尼器[5]、以及各类固态和液态阻尼装置[6-7]等,机械阻尼装置调试比较复杂,难以维护,特别是对于多模态耦合下的结构振动其设计参数难以确定,效果不理想,而且对于长吊(拉)索结构,安装位置的限制也极大地影响了其减振效果,另外对于起振负阻尼较大的柔细结构,其延时效应明显.结构措施主要通过提高结构频率和刚度使其起振风速增大、振动响应减小,目前常用的是在吊(拉)索中添加辅助索[8-9]和分隔器[10],虽然其施工方便,但影响工程美观.本文所述的西堠门大桥吊索风致振动机理复杂,无法采用气动措施减振,另外吊索起振负阻尼很大,并且受安装高度和施工条件限制难以采用机械阻尼措施,依据参考文献[10-11],决定采用加装分隔器的减振方案,依据气弹模型试验初步确定尾流驰振附加抖振是其大幅风振的原因之一,通过其临界风速公式和试验结果设计了吊索的分隔器安装方案,最后由试验和实测数据验证了方案的有效性.
1工程背景
西堠门大桥作为浙江省舟山大陆连岛工程的重要组成部分,为中国第一、世界第二跨度的钢箱梁悬索桥.大桥是两跨连续悬索桥,主跨1 650 m,主缆矢高为165 m,边跨578 m,吊点间距为18 m.大桥吊索采用四根索股一组的骑跨式,螺旋线式截面外形,靠近桥塔的最长吊索达到169 m,其单根索股截面直径仅为88 mm,而其邻近的2#和28#吊索长度和直径分别为160 m和88 mm,而其单根索股所受应力仅为最长吊索的一半,恒载索力不到其最小破断拉力的10%.如此长细轻柔的吊索使得其风致振动问题十分严重,而且由于各索股的纵横桥向间距仅分别为300 mm和600 mm,使得各索股的单独振动会引起相互碰撞,极大地影响使用寿命与行车安全.所以采取合适的抗风减振措施来解决西堠门大桥细长吊索的大幅风致振动是目前急需解决的问题.本文以桥塔附近振动最为剧烈的对称布置的2#和28#吊索作为对象,研究其抗风减振方案,为后续此类工程问题提供参考.西堠门大桥的总体布置和骑跨式吊索形式如图1所示.
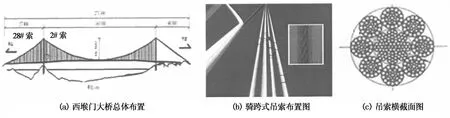
图1 西堠门大桥桥跨与吊索布置图
通过现场实测得到的2#和28#吊索环境激励数据运用随机子空间法[12]分析了吊索振动最为剧烈的前5阶频率和模态阻尼比.
运用通用有限元软件ANSYS分析得到了其模态振型.利用随机子空间法得到的吊索的前5阶频率稳定图如图2所示.频率分析结果见图2,吊索前5阶动力特性结果见表1.

频率/Hz
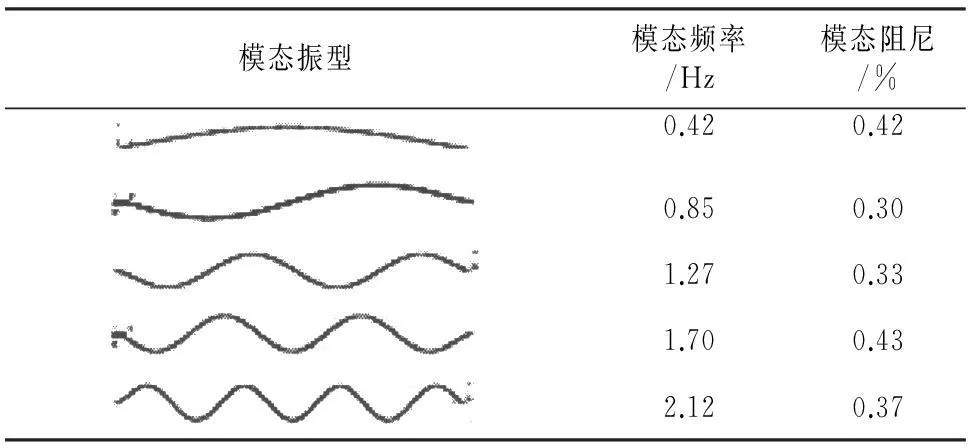
模态振型模态频率/Hz模态阻尼/%0.420.420.850.301.270.331.700.432.120.37
2分隔器减振原理
对于长细轻柔的多索股结构,其风致振动形式主要表现为索股间互相碰撞(相对运动)与索股的同步运动,分隔器绑连作用会将索股的运动分解为索股同步运动和索段相对运动(如图3所示).假设加装n个分隔器,吊索的前n阶模态与n+i(i=2,4,6,…)阶模态为4根索股的整体运动,第n+j(j=1,3,5,…)阶模态则可能为索股间相对运动或同步运动.那么索股之间的前n阶模态与n+i(i=2,4,6,…)阶模态引起的相对运动即可因分隔器的绑连作用而消除,而第n+j(j=1,3,5,…)阶模态造成的相对运动振动频率相应提高、刚度加大,在同样的激励条件下其振动响应也会减小,有利于防止吊索相碰.同步运动则会平均分配给各索股,表现为各索股的整体运动,其相当于增加了单索股的模态刚度和模态参与质量,可以有效减小某根索股的过大振动响应.另外分隔器的绑连作用减小了索股相互运动引起的气流扰动,减轻了由此引起的振动.

图3 加分隔器前后吊索振动形态的变化示意图
3吊索减振措施试验研究
3.1气弹模型的制作与相似关系拟定
为研究吊索的风致振动形态以及分隔器个数对吊索减振效果的差异,制作了缩尺比为1∶36的吊索完全气弹模型,用钢丝作为内芯,由铜丝和铝丝缠绕内芯构成外衣(模拟气动外形但不提供刚度),安装方式为4根吊索按实际的布置方式依据缩尺关系布置(A#索和B#索连线为横桥向,B#索和C#索连线为顺桥向),如图4.从而研究一个吊点4根索股的风致振动现象.
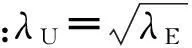
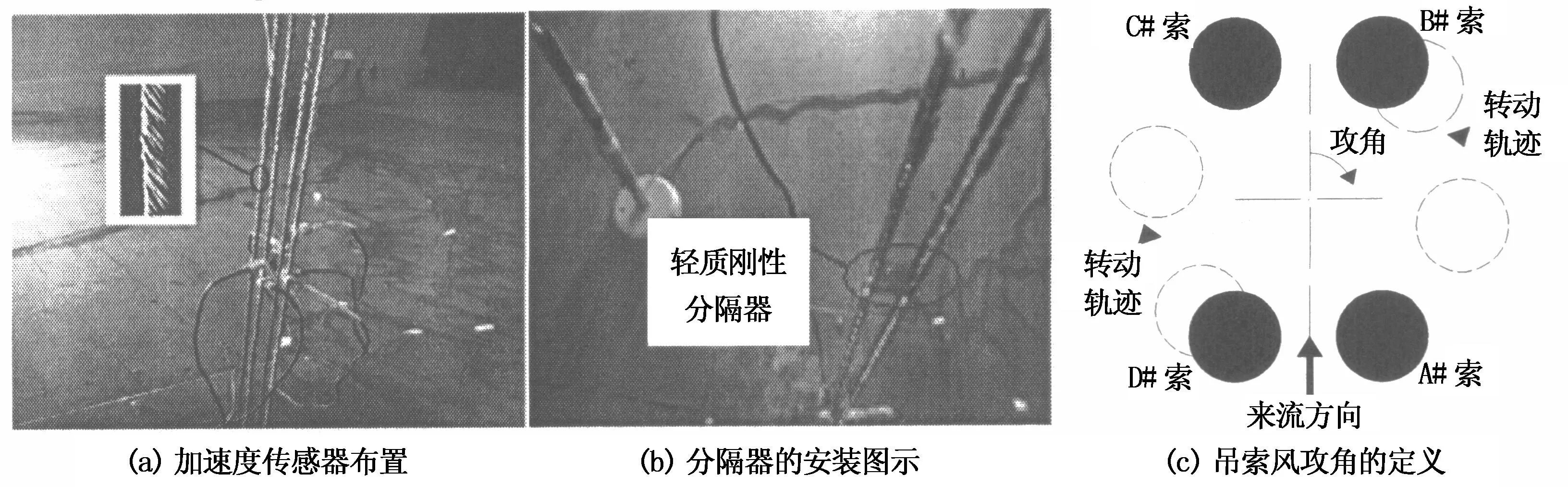
图4 吊索气弹模型测振示意图

参数名称模型值相似比原型值相似要求索长、直径、横顺桥向间距/m4.44,0.00250.016,0.0081∶36160,0.0880.6,0.3几何相似(λL=1/n)单位长度质量/(kg·m-1)0.0381∶129650量纲一致(λm=λρsl2L)单位长度质量惯矩/(kg·m2·m-1)2.68×1081∶16796160.045量纲一致(λJm=λρsλ4L)风速/(m·s-1)-1∶2.44-斯托洛哈数(λf=λU/lL)弯曲频率/Hz6.2015∶10.42斯托洛哈数(λf=λU/λL)阻尼比/%0.31∶10.3~0.5阻尼比一致(λξ=1)
试验风洞为湖南大学HD-2风洞第二试验段,模型试验区横截面宽5.5 m,高4.6 m,试验段最大风速接近15 m/s,风洞中的吊索布置如图4所示.
3.2试验索的动力特性
试验前通过对吊索施加初始激励测定了各阶频率和1~3阶模态阻尼比,频率结果和各阶模态自由衰减曲线如图5所示,结果表明模态阻尼比均为0.3%~0.5%之间,其值和模型目标值基本一致.
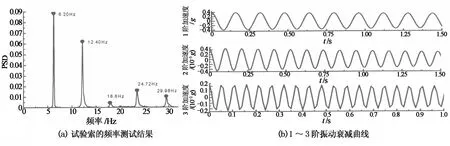
图5 试验索动力特性测试结果
3.3吊索振动形态判别
对于索类构件,风振形式有涡振、抖振、参数共振与线性内共振、尾流驰振与驰振等,本文的气弹模型采用两端固结的形式,不存在参数共振与线性内共振,由模型吊索的振动响应与风速的关系可知,吊索不存在明显的涡振区间,而且4根吊索相隔距离较近,相互干扰较大,故涡振也不是吊索大幅振动的原因,对于横截面形式接近圆形的吊索而言也不会发生经典驰振.试验发现在风速达到某一值时,处于来流下游侧的吊索会先发生椭圆轨迹运动,振动随风速的加大而逐步加大,最后变得杂乱无章,4根吊索均发生大幅振动和碰索,吊索索股在高试验风速下的典型运动轨迹如图6所示.西堠门大桥横桥向中心距与吊索直径之比为L/D=6.8,顺桥向中心距与吊索直径之比为L/D=3.4,均处于尾流影响区[14].另外试验风速段紊流度为8%左右,可能发生抖振,结合两种风振机理计算分析后认为尾流驰振主导作用下附加抖振是吊索大幅振动和碰索的关键原因.攻角调整试验结果表明15°风攻角时索振动最为剧烈,故下文均以此攻角进行减振方案研究.
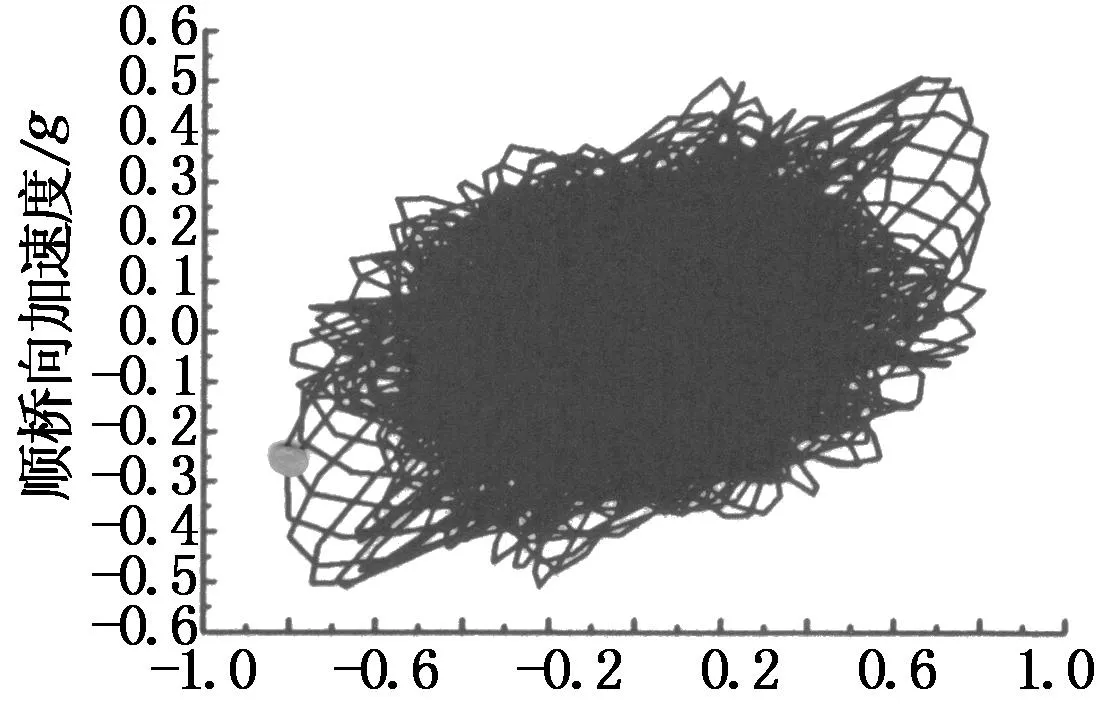
横桥向加速度/g
3.4分隔器的设计与减振效果对比
通过上节的分析决定按照尾流驰振临界风速计算方法[1,15]作为依据来设计吊索分隔器的数量,依据风速观测资料决定尾流驰振检验风速为Ucr=35 m/s(索跨中风速),按气弹模型相似比换算至试验风速为13.5 m/s.尾流驰振临界风速公式为:
(1)
式中:Uwc为尾流驰振临界风速;D为圆柱体直径;fk为模态频率,ξ为模态阻尼比;Sc为Scruton数,Sc=mξ/ρD2;m为圆柱体单位长度质量;ρ为空气密度.c为常数,当双圆柱体中心距为2~6倍圆柱体直径时,取c=25;当中心距为10~20倍圆柱体直径时,取c=80;对于本文的四索布置,按照不同分隔器下的索段起振风速拟合得到.
通过得到的c值依据式(1)可以计算吊索在检验风速下不发生尾流驰振的最低频率值,结合吊索频率计算式(2)即可得所需均匀安装的使吊索不相互碰撞的最少分隔器数量.
(2)
式中:n为频率阶次;T为恒载索力;A为截面积;l为吊索长度;ρs为索材料密度;其余符号意义同前.
最后可得分隔器安装数量计算公式为:
(3)
式中:N为所需分隔器数量.
常数c值的拟合结果如表3所示.2#与28#吊索分隔器安装建议见表4,其余吊索可按照类似方法计算.

表3 各工况吊索起振风速试验值及无量纲常数c值拟合

表4 2#与28#吊索分隔器安装建议
不同分隔器数量下的吊索气弹模型在各试验风速区间的振动时程如图7所示.通过对吊索振动状态进行频谱分析(如图8所示),可知不装分隔器时前5阶均有发生,当分别装有1个和3个分隔器时,吊索几乎分别只发生2阶和4阶振动,装4个分隔器时,前5阶振动也有发生,但振动能量比不装分隔器与只装1个和3个分隔器时大大降低.

图7 不同分隔器数量下模型测点加速度时程随试验风速的变化

图8 试验风速11.9 m/s时不同分隔器数量下的吊索振动频谱图
图9和图10统计了不同分隔器数量时各振动阶次的C#索股模型测点处顺横桥向振动加速度均方根与试验风速的关系,其中各阶振动响应运用带通椭圆数字滤波器以窄带方式提取,下文类同.由图可知加装4个分隔器后各阶的振动响应均明显减小,将最大试验风速下的响应进行对比后发现其1至5阶横桥向振动相比未装分隔器时的减小率分别为94.1%,90%,90.5%,90%与82.2%,顺桥向振动减小率分别为65.8%,81.2%,86.4%,84.8与81.2%,而且从试验现象观测到加装4个分隔器后碰索现象消除,整体位移明显减小.值得注意的是当只安装1个和3个分隔器时部分高阶振动有增大趋势,事实上从试验现象也观测到高阶运动引起的碰索.其余索股的不同分隔器数下的振动响应变化规律与C#索股基本一致,试验结果表明2#和28#索需至少安装4个分隔器.
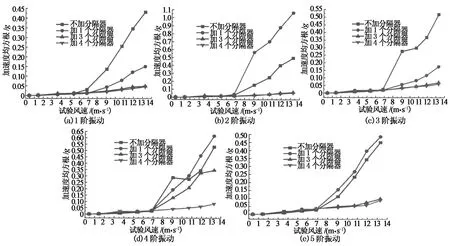
图9 不同分隔器数量时C#索股横桥向加速度响应均方根和风速的关系
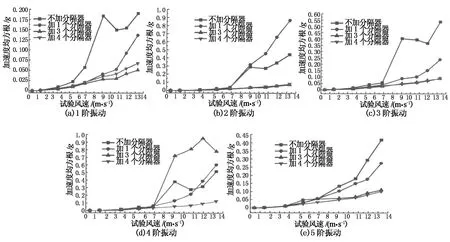
图10 不同分隔器数量时C#索股顺桥向加速度响应均方根和风速的关系
4减振措施实测验证
4.1现场监测系统简介
为了验证分隔器减振效果的有效性,作者通过安装于现场的吊索振动监控系统获取了2014年7月24日的一次大风天气下的吊索处的风速数据和吊索的振动加速度信号.通过安装有分隔器的28#吊索和未安装分隔器的2#吊索的实测信号对比,可以准确得到分隔器的减振效果.现场监控系统布置如图11(a)所示,风速测试采用螺旋桨式二维杨氏风速仪,采样频率1 Hz,安装高度为距桥面4 m的位置,风向规定如图11(b),吊索加速度测试采用941B型拾振器,采样频率为5~10 Hz,安装高度为距吊索底部14 m的位置.风速仪、加速度传感器和数据采集系统的现场照片如图12所示.
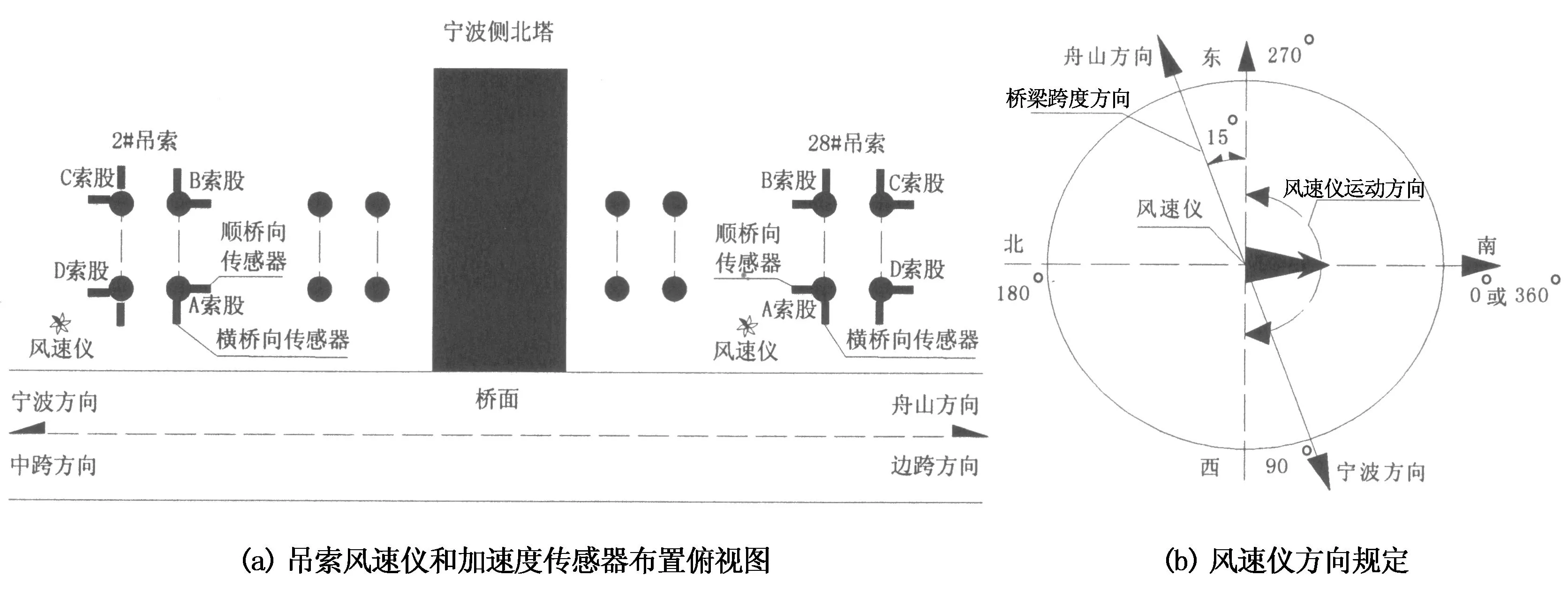
图11 加速度传感器布置与风速仪方向规定

图12 风速仪和加速度传感器以及数据采集系统的现场实物图
4.2大风天气下实测数据分析
通过某次大风天气下的观测数据,本文对关于桥塔对称的2#和28#吊索的观测数据进行了比较,28#吊索按试验方案沿吊索长度方向等间距安装了4个分隔器,而另一侧的2#吊索则未安装分隔器.图13给出了2014年7月24日全天的风向风速和加速度实测数据,并选取了用于数据研究的信号分析段.信号分析段的吊索振动典型频谱如图14所示.

图13 大风天气下的吊索位置风向、风速以及加速度观测时程数据
从频谱图中可知未安装分隔器的2#吊索,其1~5阶振动非常卓越,而加装分隔器的28#吊索无明显卓越频率,频谱分散凌乱,类似于白噪声,功率谱密度峰值相比2#吊索各索股明显减小,证明可造成大幅振动的前5阶振动能量大大降低.信号分析段对应时间的风向为300°左右,按照图11(b)对风向的规定,可知其为与横桥向成30°左右的风向角从西北方向吹向东南方,因此2-B#索股与28-C#索股在此风向角下属于同方位索股,另外由图给出的信号分析段对应的风速可知,2#和28#吊索位置对应的风速基本一致,故比较2-B#索股与28-C#索股的振动响应情况就能准确反应分隔器对吊索的减振效果.通过对信号分析段按1 min平均时距做加速度均方根统计,得到了相应加速度均方根随时间的变化如图15所示.从图中看出,安装分隔器后的28-C#索股的振动响应明显要小于2-B#索股的响应值,加装了4分隔器的28-C#索股相比2-B#索股其横桥向1至5阶振动响应均值分别减小了66.7%,60%,57.1%,60%与56.3%,根据现场观测录像2#索有明显碰索现象,而加装分隔器的28#索则未出现,从而验证了分隔器的良好的减振效果.
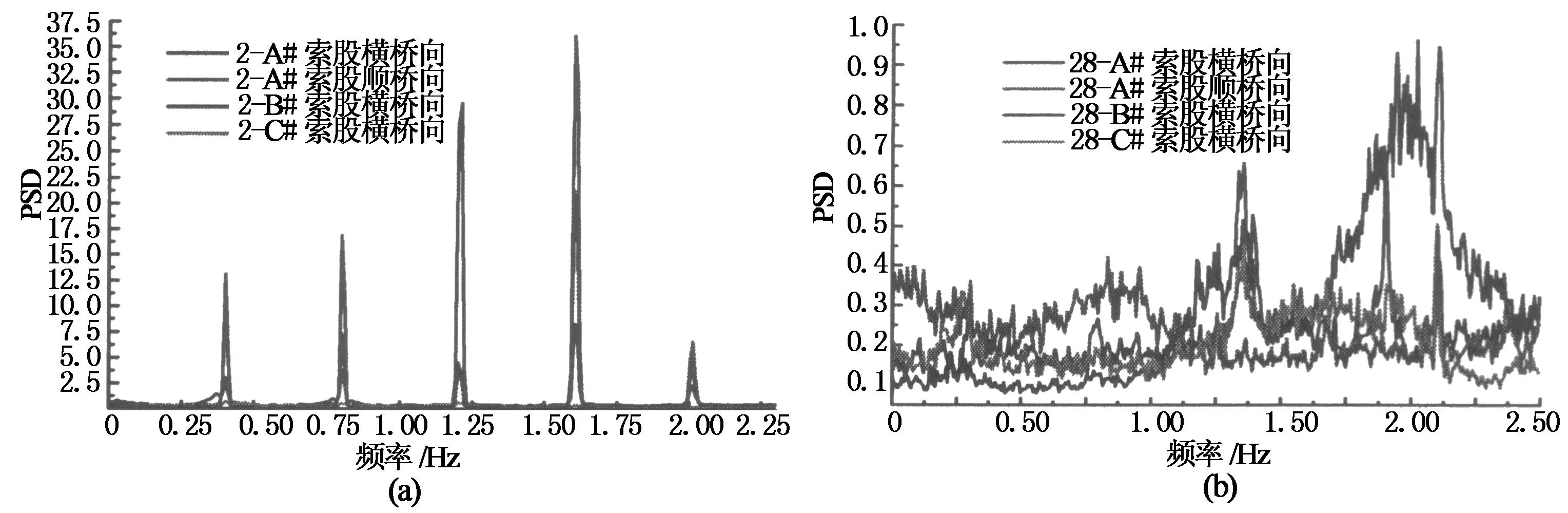
图14 信号分析段得到的2#与28#吊索各索股振动典型频谱图


图15 不同振动阶次时2-B#与28-C#索股横桥向加速度响应均方根和风速的关系
5结论
1)制作了西堠门大桥的骑跨式矩形排列吊索的完全气弹模型,对其气动外形进行了准确模拟,并且通过风洞试验再现了多索股吊索的大幅振动和碰索现象.
2)依据试验结果初步确定尾流驰振附加抖振是吊索大幅振动和碰索的关键原因,但由于没有模拟吊索两端实际边界条件,尚无法确定是否存在参数振动和线性内共振,需进行后续研究.
3)依据尾流驰振理论和吊索气弹模型试验结果拟合得到了尾流驰振临界风速公式中适用于西堠门桥吊索布置的常数c值,并设计了满足桥址处检验风速下不发生尾流驰振的需均匀安装的最少分隔器数量.
4)最后通过吊索完全气弹模型试验得到的响应结果和现场实测数据验证了分隔器对吊索多索股减振的有效性,索股的各阶模态减振率达55%~95%,其成功应用可为类似工程提供参考.
参考文献
[1]陈政清.桥梁风工程[M].北京:人民交通出版社,2005:139-162.
CHEN Zheng-qing. The bridge wind engineering[M]. Beijing: China Communication Press, 2005:139-162.(In Chinese)
[2]李宏男,李忠献,祁铠,等.结构振动与控制[M].北京:中国建筑工业出版社,2005:1-277.
LI Hong-nan, LI Zhong-xian, QI Kai,etal. Structure vibration and control[M].Beijing: China Building Industry Press, 2005:1-277. (In Chinese)
[3]李寿英,钟卫.缠绕螺旋线斜拉索气动性能的试验研究[J].土木工程学报,2013,46(7):108-115.
LI Shou-ying, ZHONG Wei. Experimental study on the aerodynamic characteristics of stay cables with helical lines [J]. China Civil Engineering Journal, 2013, 46(7):108-115. (In Chinese)
[4]VECCHIARELLI J, CURRIE I G, HAVARD D G. Computational analysis of aeolian conductor vibration with a stockbridge-type damper [J]. Journal of Fluids and Structures, 2000, 14(4):489-509.
[5]陈政清, 黄智文, 王建辉,等. 桥梁用TMD的基本要求与电涡流TMD[J]. 湖南大学学报:自然科学版, 2013, 40(8):6-10.
CHEN Zheng-qing, HUANG Zhi-wen,WANG Jian-hui,etal. Basic requirements of tuned mass damper for bridges and the eddy current TMD[J].Journal of Hunan University:Natural Sciences, 2013, 40(8):6-10. (In Chinese)
[6]汪正兴, 王波, 钟继卫,等. 液体质量双调谐减振器(TLMD)研究与应用[J]. 桥梁建设, 2011(1):10-13.
WANG Zheng-xing,WANG Bo,ZHONG Ji-wei,etal. Research and application of tuned liquid and mass damper (TLMD)[J].Bridge Construction,2011(1):10-13. (In Chinese)
[7]王修勇, 陈政清, 倪一清. 斜拉桥拉索风雨振观测及其控制[J]. 土木工程学报, 2003, 36(6):53-59.
WANG Xiu-yong, CHEN Zheng-qing, NI Yi-qing. Rain-wind induced vibration and its control on stay cables of cable-stayed bridges[J]. China Civil Engineering Journal, 2003, 36(6):53-59. (In Chinese)
[8]周亚刚. 斜拉索—辅助索系统动力特性和减振研究[D]. 上海:同济大学土木工程学院, 2007:1-16.
ZHOU Ya-gang.Dynamic characteristics and vibration mitigation of stay cables using cross ties[D]. Shanghai:College of Civil Engineering ,Tongji University, 2007:1-16. (In Chinese)
[9]YAMAGUCHI H, NAGAHAWATTA H D. Damping effects of cable cross ties in cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54(2):35-43.
[10]王昕. 覆冰导线舞动风洞试验研究及输电塔线体系舞动模拟[D]. 杭州:浙江大学建筑工程学院, 2011:9-14.
WANG Xin.Wind tunnel test on galloping of iced conductors and galloping simulation for transmission tower-line system[D].Hangzhou:College of Civil Engineering and Architecture, Zhejiang Univesity, 2011:9-14. (In Chinese)
[11]LAURSEN E, BITSCH N, ANDERSEN J E. Analysis and mitigation of large amplitude cable vibrations at the great belt east bridge[J].IABSE Symposium Report. International Association for Bridge and Structural Engineering, 2006, 91(3): 64-71.
[12]常军, 张启伟, 孙利民. 随机子空间方法在桥塔模态参数识别中的应用[J]. 地震工程与工程振动, 2006, 26(5):183-187.
CHANG Jun, ZHANG Qi-wei, SUN Li-min. Application of stochastic subspace identification inmodal parameteridentification of bridge tower[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5):183-187. (In Chinese)
[13]李永乐, 王涛, 廖海黎. 斜拉桥并列拉索尾流驰振风洞试验研究[J] . 工程力学, 2010, 27(s1):216-227.
LI Yong-le,WANG Tao,LIAO Hai-li. Investigation on wake galloping of parallel cables in cable-stayed bridge by wind tunnel test[J]. Engineering Mechanics,2010, 27(s1):216-227. (In Chinese)
[14]TOKORO S, KOMATSU H, NAKASU M,etal. A study on wake-galloping employing full aeroelastic twin cable model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2):247-261.
[15]PAIDOUSSIS M P, PRICE S J, LANGRE E D. Fluid-structure interactions: cross-flow-induced instabilities[M].Town of Cambridge: Cambridge University Press,2010:155-210.
Research and Application of Vibration Control Method for Hanger Cables in Long-span Suspension Bridge
CHEN Zheng-qing1†, LEI Xu1,HUA Xu-gang1,LI Shou-ying1,YAN Yong-xian2, WEN Qing1,NIU Hua-wei1
(1. Wind Engineering Experiment Research Center, Hunan Univ, Changsha,Hunan410082, China; 2.Zhejiang Communications Investment Group CO LTD, Hangzhou, Zhejiang310014, China)
Abstract:The hanger cables of long-span suspension bridges are susceptible to wind-induced vibration as they have low natural frequencies and low mechanical damping. In this paper, the wind-induced vibration problem of the hanger cables of Xihoumen Bridge was investigated to research the vibration control method. Firstly, the dynamic characteristics of the hanger cables were obtained by environmental incentive method. Then, the scheme of installing spacers was determined by theoretical analysis and wind tunnel experiments, in addition, the influence of the number of spacers on vibration-reduction efficiency was investigated in the experiments. Finally, according to the field test of the wind-induced vibration of two hanger cables with and without spacer respectively conducted in strong wind weather, the results indicates that after installation of the spacers, the collision phenomenon between the strands is eliminated. Moreover, the vibration of different modes of the hanger cable is significantly reduced by 55%~95%.
Key words:long-span suspension bridge; hanger cable; wind effects; spacer; full aeroelastic model; field tests
中图分类号:U441.3
文献标识码:A
作者简介:陈政清(1947-),男,湖南湘潭人,湖南大学教授,博士生导师†通讯联系人,E-mail:414972139@qq.com
*收稿日期:2015-04-10基金项目:国家自然科学基金资助项目(51422806, 91215302),National Natural Science Foundation of China(51422806,91215302)
文章编号:1674-2974(2016)01-0001-10
