高层建筑气动弹性模型风洞试验研究*1
2016-04-25李秋胜
李秋胜,陈 凡
(1.湖南大学 土木工程学院,湖南 长沙 410082;2. 香港城市大学 土木与建筑工程系,香港 999077)
高层建筑气动弹性模型风洞试验研究*1
李秋胜1,2†,陈凡1
(1.湖南大学 土木工程学院,湖南 长沙410082;2. 香港城市大学 土木与建筑工程系,香港999077)
摘要:以高层建筑为研究背景,制作了气动弹性模型,通过风洞试验测得结构的时程响应结果,采用频谱分析求得结构的动力特性,采用自然激励技术法(NExT)和ARMA模型时序法以及改变模态阶数的方法获得结构的气动阻尼比,研究了结构气动阻尼比随风速的变化规律.在强风下,对顺风向的加速度响应时程结合滤波方法,消除横风向能量转移的影响,同时发现了涡激共振现象.考虑气动阻尼影响的情况下,刚体模型测压和测力得到的峰值加速度响应结果,与气动弹性模型风洞试验结果十分接近,验证气动弹性模型风洞试验结果的正确性.对于刚体模型,不考虑气动阻尼时,峰值加速度比气动弹性模型试验结果大很多,差值最大达到41%,但在某种工况下,气动阻尼的影响使结构的响应值增大,验证了考虑气动耦合作用在高层抗风研究中的必要性.
关键词:高层建筑;气动弹性模型;风洞试验;动力特性;气动阻尼;峰值加速度
Kareem and Gurley[1]和Vickery and Steckley[2]得出了折算风速在6到10之间,高层建筑的气动阻尼会出现正的最大值,随后气动阻尼随折算风速的增加而急剧减小,当折算风速在10~11之间时会出现负的最大值,加剧结构的风振响应.由此可见,气动阻尼对高层建筑风致振动响应的影响有时是不能忽略的,特别是当结构的气动阻尼出现负值时,会使结构总阻尼降低,导致高层建筑动力响应较高,这在高层建筑抗风设计研究中应引起重视.
Kareem(1982)[3]在测压试验中引入了气动阻尼比,得出了响应的简化计算方法;全涌(2001)[4]将气动弹性模型结果与高频测力天平试验结果进行了对比,并在2003年[5-7]用随机减量法研究顺风向及横风向气动阻尼;黄东梅(2008)[8]讨论了气动弹性模型模态分析的3种方法,给出了各方法的适用情况;吴海洋(2010)[9]运用改进的随机减量技术,分析了风场类别、结构阻尼比等因素对横风向气动阻尼比的影响.
在已有研究的基础上,本文以高层建筑为研究背景,制作了气动弹性模型,通过模拟结构的质量和刚度,测量出结构的时程响应结果,模拟高层建筑与风的相互作用过程,以及气动反馈效应,识别结构的动力特性以及对风振响应起重要作用的气动阻尼比,研究气动阻尼比随风速的变化规律.同时制作相同外形尺寸的刚性测压模型和测力模型进行风洞试验研究,通过考虑气动阻尼的影响,验证气动弹性模型试验结果的正确性.
1试验概况
1.1试验设备
气动弹性模型试验是在湖南大学建筑与环境风洞实验室中完成的.
在大气边界层风场模拟及试验过程中采用澳大利亚TFI公司的眼镜蛇三维脉动风速仪、A/D板、PC机和专用软件组成的系统来测量风场风速、湍流度等数据.
试验过程中,采用加速度传感器和激光位移计对气动弹性模型的加速度和位移进行采集.通过由电子扫描阀系统、PC机以及自编的信号采集及数据处理软件组成的一套系统完成多点瞬态风压同步测量试验动态数据的采集.高频动态测力天平试验采用6分量(包括3个方向的力和力矩)高频底座动态天平进行测试.
1.2风场模拟结果
本次试验采用C类地貌,按1∶300的缩尺比进行大气边界层模拟,参考高度选取模型的顶部高度,即0.8 m高度处,试验风速为10 m/s,依据《建筑结构荷载规范》(GB5009-2012)[10]中规定,地面粗糙度系数α为0.22,10 m高度处名义湍流度I10为0.23.风场模拟情况如图1所示.
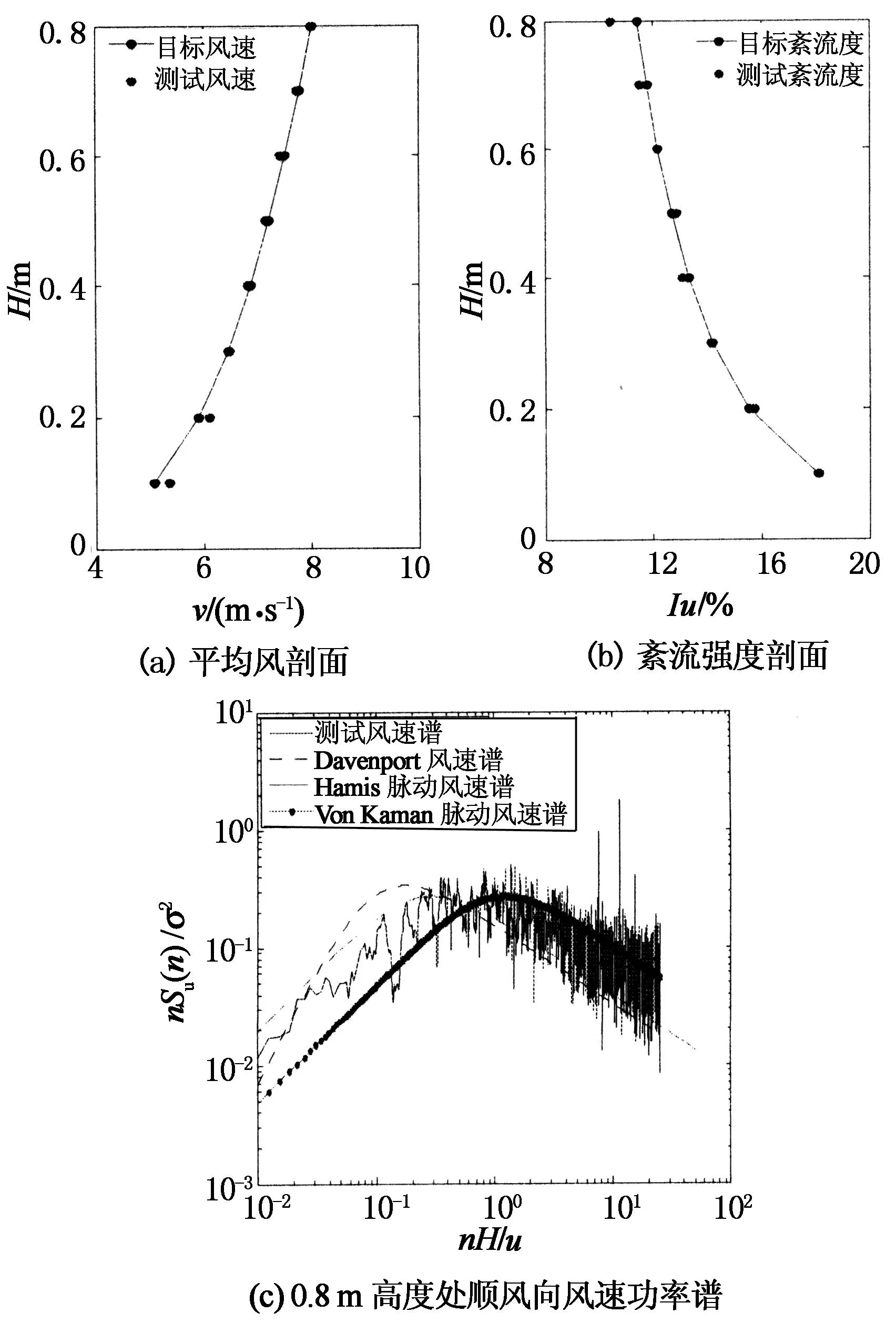
图1 C类风场模拟结果图
1.3试验模型设计
气动弹性模型采用芯棒模拟结构的刚度、外衣模拟结构的外形尺寸、配重块调节结构质量的形式制作而成的.芯棒采用无缝方形镀锌钢管制作,截面外尺寸为20 mm×20 mm,截面厚度为1 mm.外衣采用透明的有机玻璃制成,有机玻璃的厚度为2 mm.为了不影响结构的整体刚度,模型制作时将外衣共分为5段,每段之间留1~2 mm的间隙,并通过铝制螺栓将外衣固定在芯棒上.除了芯棒和外衣所提供的质量外,结构的质量可通过在外衣内侧粘贴铁片作为配重块进行控制和调节.结构的总重量约为4.57 kg.为了实现底部固结,将钢板与芯棒焊接在一起,并与地面牢固连接.结构模型图如图2所示.

图2 气动弹性模型图
试验模型采用1∶300的几何缩尺比,模型的截面尺寸为101.6 mm×152.4 mm,模型高度为800 mm.通过控制风速比得到结构模型与原型的频率比.试验中,控制风速比为1∶4.71,则频率比定为63.69∶1.相应地可计算得到本次试验模型的质量、刚度、位移、加速度等的相似系数,见表1.

表1 模型与原型的相似系数
刚性测压模型和测力模型采用同气动弹性模型相同的几何缩尺比、截面尺寸和模型高度,测压模型为采用ABS透明板材制作而成的刚性模型,具有足够的刚度和强度,模型外表面共布置了480个测点.测力模型为采用高强轻质木板制作而成的刚性模型,内部采用泡沫填充.
2试验结果分析
试验结果分析包括动力特性测试结果分析、气动阻尼识别结果分析以及3种试验方法得到的加速度响应值的对比分析,以验证气动弹性试验的正确性.
2.1风洞试验动力特性测试结果
在气动弹性模型的680 mm和340 mm高度处的长边方向和短边方向分别布置了激光位移计.在模型的708 mm和340 mm高度处的截面两个方向分别布置了加速度传感器.在进行模型振型测定时,增加一种工况,即在模型的708 mm和525 mm高度处的截面两个方向分别布置加速度传感器.设沿垂直于模型长边方向为X方向,沿垂直于模型短边方向为Y方向.试验过程中采样频率均为125 Hz,每一个信号数据包括6 000~20 000个离散数据,并进行8个通道的同步测量.
模型的动力特性测试采用锤击法.分别沿垂直于短边方向(Y方向)、垂直于长边方向(X方向)对结构进行初始激励,获得各测点的自由衰减振动信号时程,对各测点的响应信号进行消除趋势项、平滑处理,FFT变换得到幅值谱图,再对各测点之间进行互谱分析,确定频率和振型,最后将衰减曲线采用对数衰减率法得到固有阻尼比值.此外,为了减小试验误差,本次试验采用采集多组数据取均值的方法求得结构的自振频率、振型和阻尼.动力特性测试结果见表2.振型结果如图3.
为了获得更加明显的气动耦合现象,在模型设计时降低了设计刚度,使动力特性测试得到的自振频率值明显偏低,如表2中,结构X,Y方向的一阶自振频率值在8.5~8.7 Hz范围内,根据表1中规定的频率相似系数值,可以算出实际的一阶自振频率值范围在0.133~0.137 Hz,这比实际240 m高度的高层建筑的自振频率要低.但这并不会影响3种试验方法结果的对比,因此该设计并不会影响试验目的.
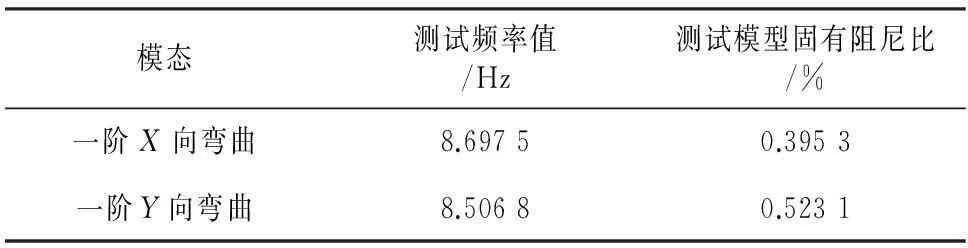
表2 动力特性测试结果
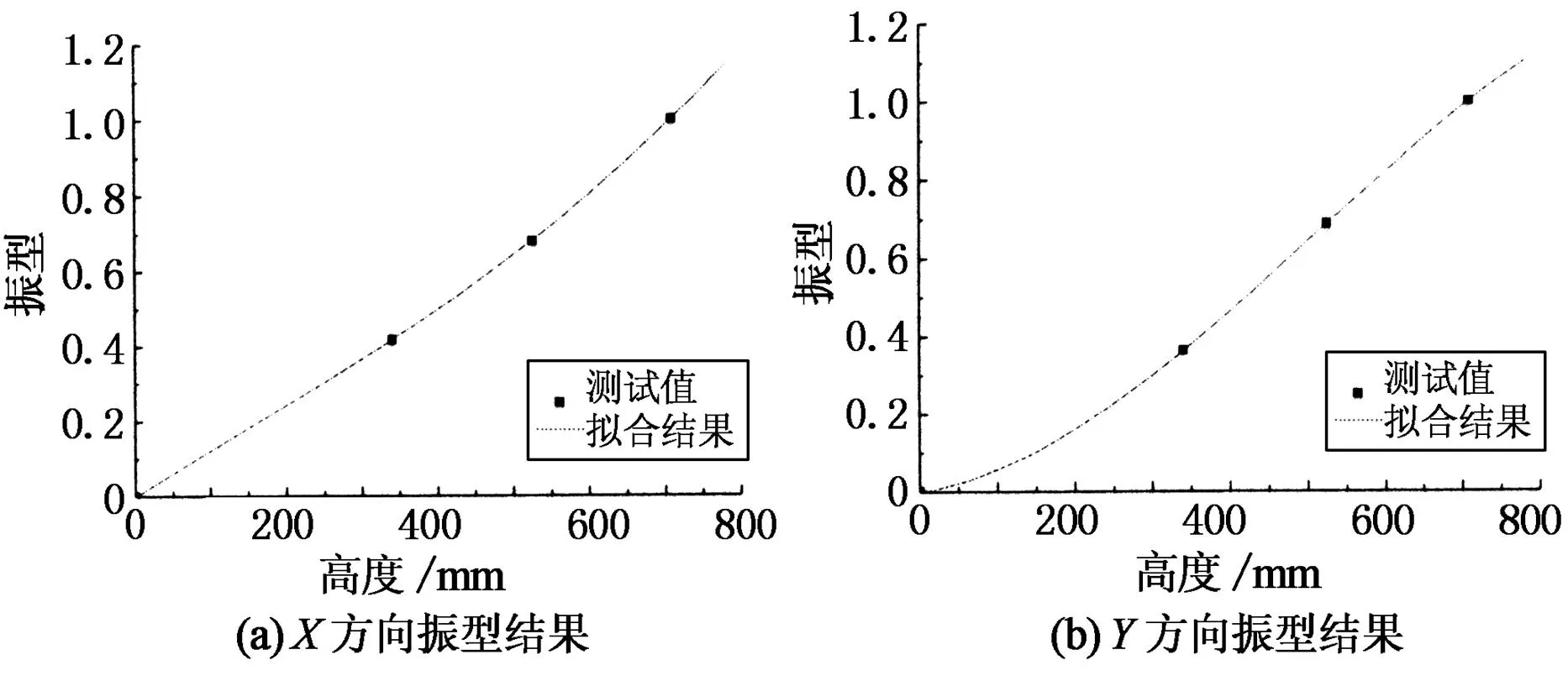
图3 测试振型图
在求解固有阻尼比时,由于模型设计的X方向频率与Y方向频率比较接近,锤击时,锤击点又很难保证作用在模型测点高度截面的轴线上,导致两个方向上都可能产生振动,造成了能量在两个方向的传递与分散,出现了“拍”现象,如图4所示.
针对这一现象,本文在全涌[5]提出的方法基础上将X,Y两个方向的振动幅值进行平方和开平方,将正的幅值和负的幅值分离开,得到了在零附近上下振动的衰减曲线.以锤击长边(X方向)为例,消除“拍”现象后可以得到如图5的衰减曲线,进而应用于结构固有阻尼比的求解过程中.
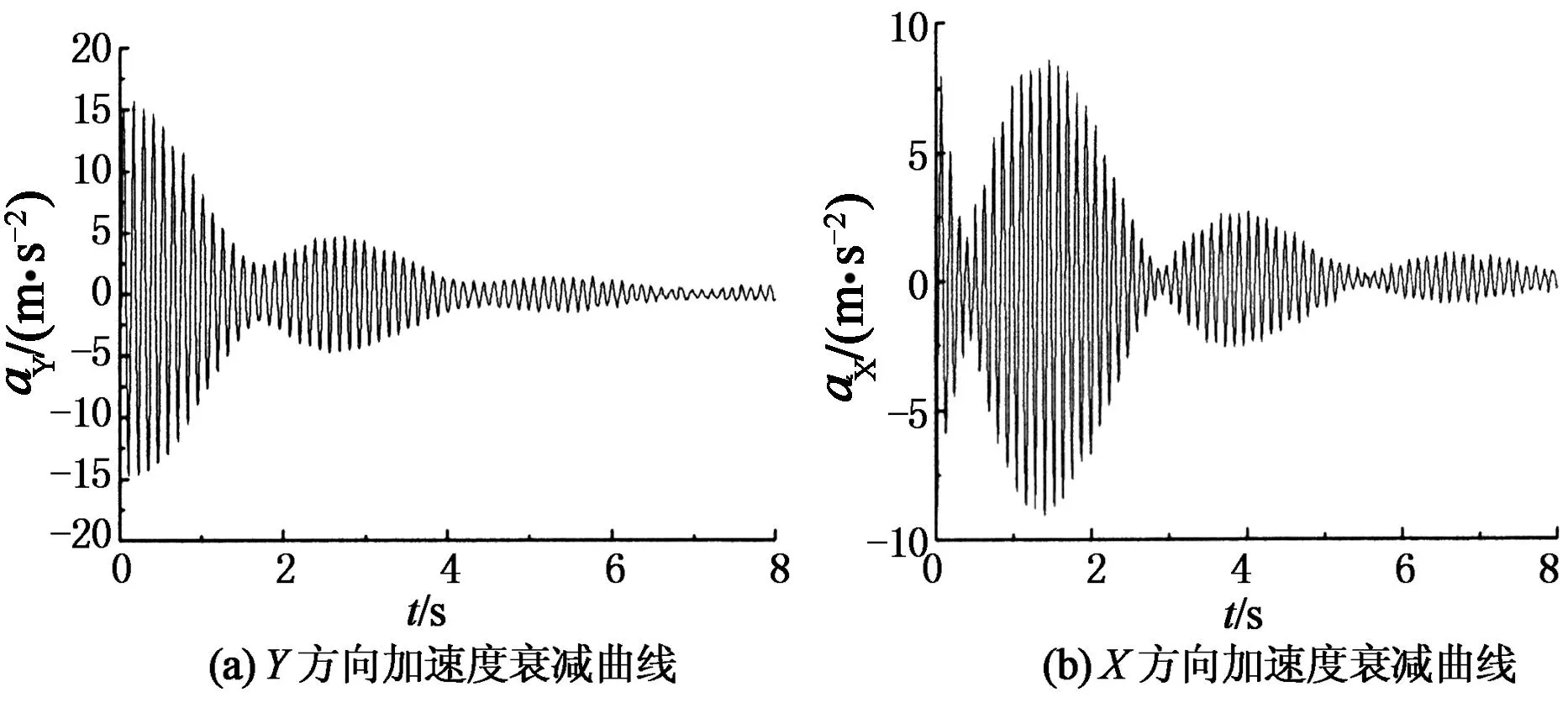
图4 “拍”现象

图5 衰减曲线
2.2风洞试验气动阻尼识别测试结果
2.2.1试验及理论方法
在进行气动弹性模型风洞试验气动阻尼识别过程时,在模型680 mm和340 mm高度处的长边方向和短边方向分别布置了激光位移计.在模型的708 mm和340 mm高度处的截面两个方向分别布置了加速度传感器,如图6(a)所示.进行7个风向角的测定,风向角范围为0°~90°,风向角间隔为15°,逆时针旋转.控制风速为0 m/s,6 m/s,8 m/s,10 m/s,12 m/s,15m/s,0°风向角的规定如图6(b)所示.从风向角的规定图可以看出,0°来流方向与Y轴的正方向相一致.
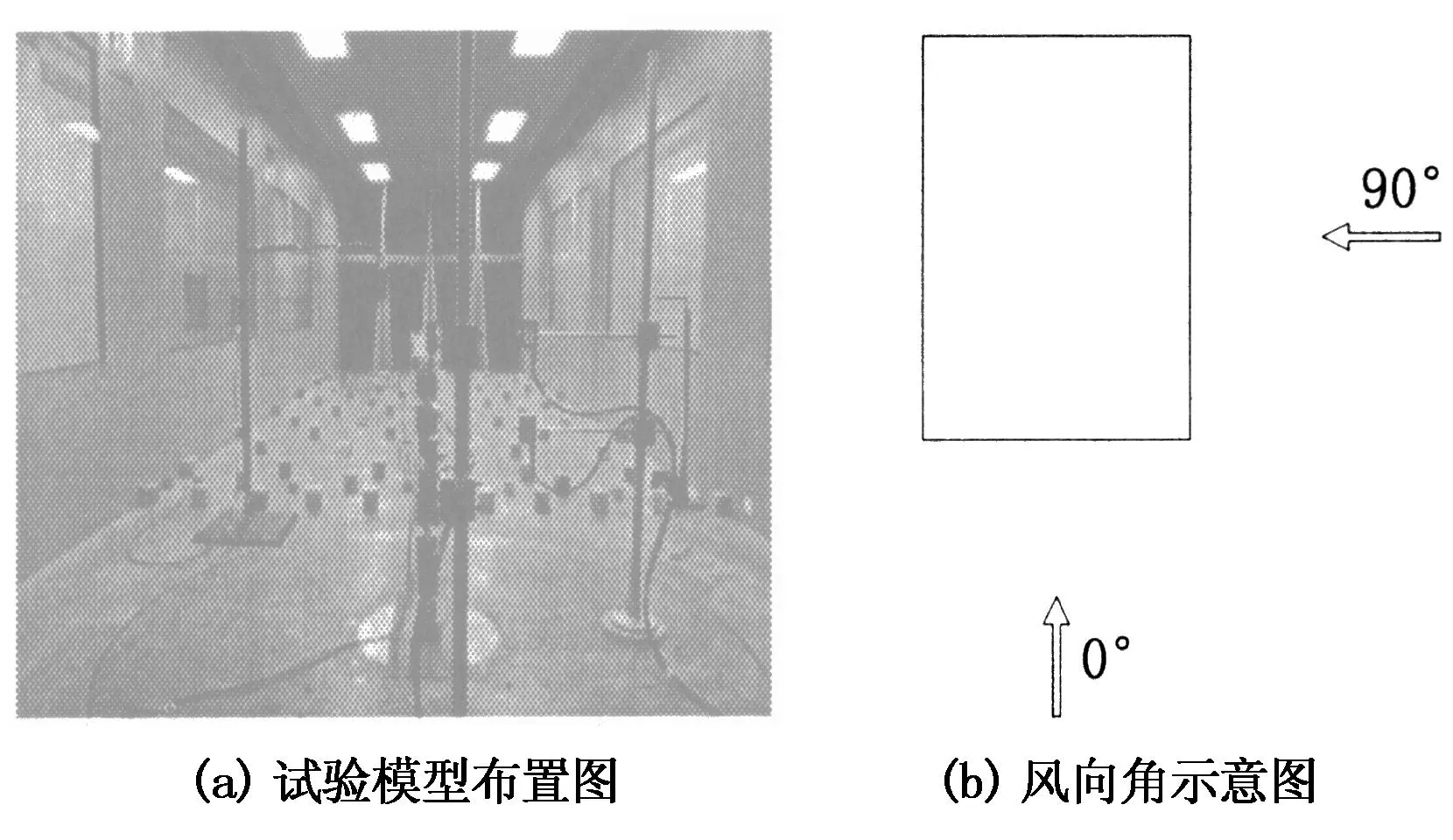
图6 试验模型布置及风向角示意图
将测试得到的响应信号进行消除趋势项、平滑处理以及滤波处理,然后采用NExT法将采样得到的振动响应数据进行互相关计算,得到实测信号的互功率谱,再通过IFFT得到实测互相关函数.将计算出来的互相关函数进行ARMA模型时序法的时域模态识别法分析,识别结构的气动阻尼比.在采用NExT法且测点数量较多时,将其中一个测点选为参考点,计算其他测点同该参考测点的互相关函数,作为ARMA法的输入数据.
从试验测得的加速度时程曲线图中可以看出,加速度响应只在0°和90°风向角下出现最大值,且在这两种风向角下横风向加速度响应均大于顺风向加速度响应.因此在气动阻尼识别过程中只选取了8,10,12,15m/s控制风速下采集到的0°和90°风向角下的加速度响应时程数据进行气动阻尼的识别.
2.2.2 数据处理
对加速度传感器进行编号,将位于模型708 mm高度处垂直于短边方向(即0°风向角下顺风向,90°风向角下横风向)和垂直于长轴方向(即0°风向角下横风向,90°风向角下顺风向)的加速度传感器标记为A708-1和A708-2;将位于模型340 mm高度处垂直于短边方向(0°风向角下顺风向,90°风向角下横风向)和垂直于长轴方向(0°风向角下横风向,90°风向角下顺风向)的加速度传感器标记为A340-1和A340-2.
为了增加结果的精确性,减小模态参数识别的时域分析方法中所包含的较多噪声干扰的影响,首先对响应时程数据进行自谱分析,找到峰值点所对应的一阶自振频率.
以8 m/s控制风速0°风向角下的顺风向加速度响应时程数据为例,测得顺风向的自振频率为8.514 4 Hz,由于气动刚度的影响,测得的频率值与锤击法测得的频率不完全相等.
将A708-1和A340-1采集到的加速度响应时程数据运用NExT法和IFFT处理,得到互相关函数,代替脉冲响应函数作为ARMA模型时序法的输入数据,得到总的阻尼比ξ.在上述分析过程中,为了减少噪声干扰,可采用改变模态阶数的方法,在模型的拟合曲线与实测曲线吻合得较好的前提下,找到与上一步测得的一阶自振频率值接近的稳定频率值所对应的阻尼比作为最终结果,因此该组数据识别的总阻尼比ξ为0.965 5%,所对应的频率值为8.514 4 Hz.由ξa=ξ-ξs,ξa为气动阻尼比,ξs为结构的固有阻尼比0.523 1%,可得8 m/s控制风速下模型在0°风向角下顺风向的气动阻尼比ξa为0.442 4%.
图7即为上述控制风速为8 m/s时,0°风向角下顺风向总阻尼比的识别过程.采用同样的识别方法可得到模型在不同风速下气动阻尼的变化曲线图,这里不再一一列出.
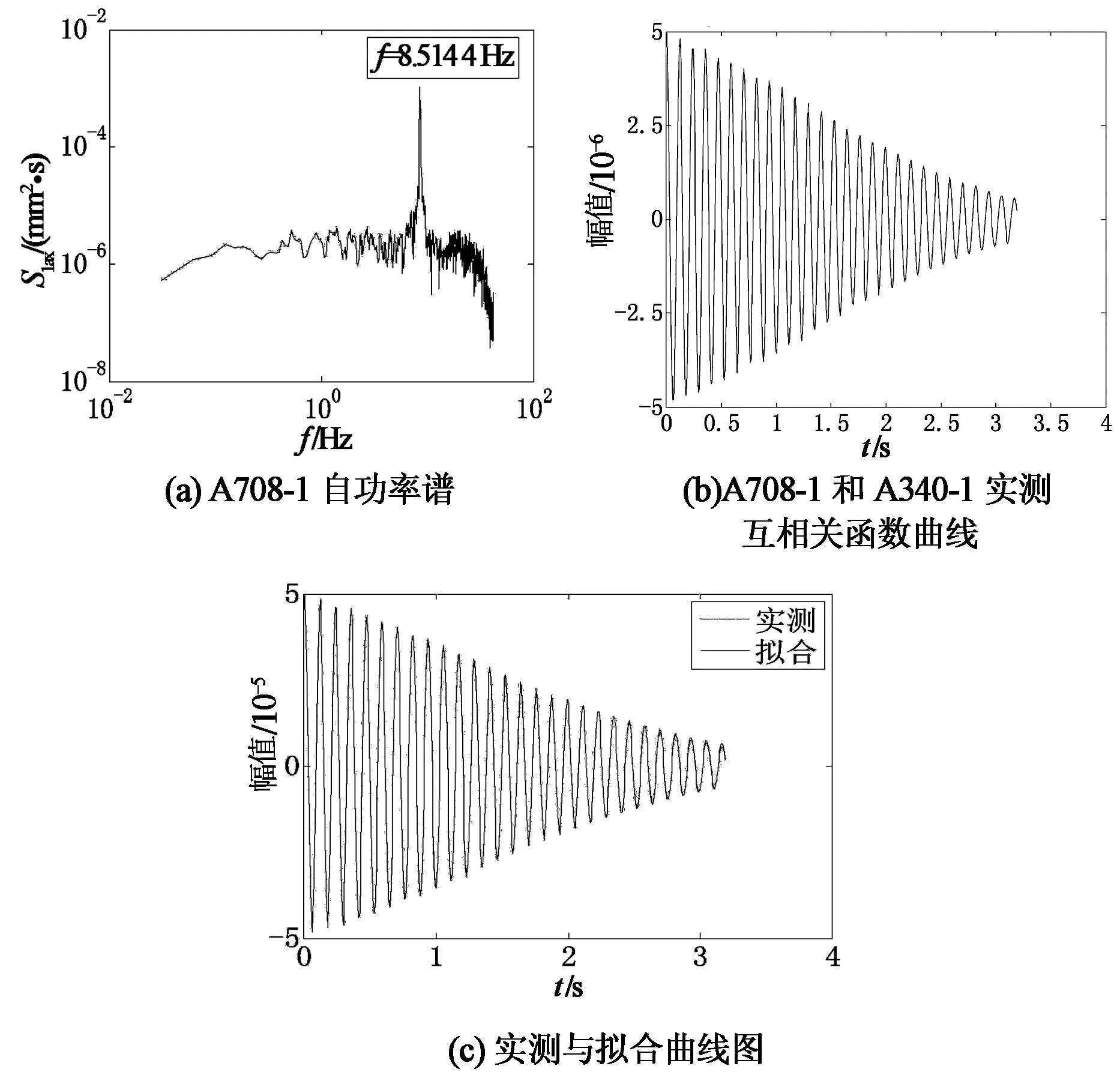
图7 8 m/s控制风速下0°顺风向阻尼识别图
当控制风速达到15 m/s时,在长边迎风,即90°风向角下,无论是横风向还是顺风向的响应时程数据的自谱分析都只能求得一个频率值,该频率值与垂直于短边方向的自振频率值比较接近.这是因为在此控制风速下,横风向结构较柔,其折算风速达到14,达到了结构的临界风速,自振频率接近于旋涡脱落频率,结构出现了共振现象.图8中,名义上的斯托罗哈数频率从4.211 4 Hz增大到8.300 8 Hz,当控制风速为15 m/s时,与自振频率对应的峰值重合,产生了共振现象.

图8 控制风速8~15 m/s的90°风向角的横风向加速度功率谱图
结构达到共振状态时,横风向的响应有了很明显的提高,90°风向角下,在进行结构顺风向,即垂直于长边方向的气动阻尼识别时,通过NExT法得到的衰减曲线出来了“拍”现象,如图9(a)所示.
在图9(b)的自谱曲线中可以明显地看到,衰减曲线除了在自振频率处出现最大峰值外,略大于自振频率的频率处出现了次峰值,这部分能量在图9(a)中就表现为2~3 s期间的幅值随时间的增加又增大的现象,这个现象会影响气动阻尼求解的准确性,为此,需要采用滤波的方法将噪声频率过滤掉.本次试验采用了带阻滤波方法[11],最小截止频率和最大截止频率分别为8.5 Hz和9.3 Hz.滤波前后的对比图如9(c)所示.

图9 带阻滤波方法
2.2.3测试结果
在进行气动阻尼分析过程中采用了折算风速VH/(fB),其中VH为模型高度处的风速值,f为结构的自振频率,B为迎风面的迎风长度.气动阻尼比随折算风速的变化曲线如图10所示.从图中可以看出,在同一风向角下,横风向的气动阻尼比总体大于顺风向的气动阻尼比.
对于横风向,受工况所限,如图10(a)所示,0°风向角下横风向(即垂直于长边方向)经计算得到的折算风速在5~9范围内,折算风速超过9的曲线段没有体现,所以其气动阻尼比只体现出随折算风速的增大而不断上升的区段,而未体现气动阻尼比随折算风速的增大而下降的趋势.
但对于90°风向角下横风向(垂直于短边方向)的气动阻尼比,如图10(c)所示,折算风速体现了8~14的变化区间,当折算风速在8~9范围内变化时,横风向的气动阻尼比随折算风速的增大而增大,当折算风速继续增大时,气动阻尼比开始随折算风速的增大而减小,当折算风速达到13~14时,气动阻尼比出现负值,但该负值的绝对值并不大,很接近零.与文献[6]中C类风场在结构阻尼比为0.6%时的横风向气动阻尼比的变化规律是比较一致的.

图10 气动阻尼比随风速的变化曲线图
对于顺风向,同样由于受到工况所限,如图10(d)所示,90°风向角下顺风向测得的折算风速的变化范围为5~9,变化范围太小,气动阻尼只测到随折算风速的增大而下降的区段,这并不能完全反映顺风向气动阻尼比与折算风速之间的变化规律,而只是局部反映出在折算风速的某个变化区间内气动阻尼比的变化特点,而在文献[12]中也有类似的现象出现.即在与本实验相同深宽比的前提下,折算风速达到8~10时,顺风向气动阻尼比出现下降段.
从图10(b)中可以看出,折算风速的变化范围为8~14,在折算风速为9~11时,0°风向角下顺风向气动阻尼比随折算风速的增大而减小,随后随折算风速的增大而一直保持增大的趋势.
综上所述,在折算风速变化范围较大的情况下,即图10(b)和图10(c)所示,顺风向气动阻尼比随风速的变化曲线大体上随折算风速的增大而呈上升趋势,但不可忽视其中存在的下降段;横风向气动阻尼比随风速的变化曲线随折算风速的增大先上升后下降,当折算风速达到一定值时,会出现气动阻尼比小于0的情况,应引起重视.
2.3加速度响应值的对比分析结果
2.3.1试验及理论方法
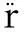
(1)
(2)
(3)
(4)
(5)
(6)

其次,对测力试验情况作简要的介绍.试验过程
中,关于风向角方向和风向角间隔的规定同测压试验.数据处理采用基于基底弯矩的阵风因子法.图11只列出控制风速为8 m/s时90°风向角下顺风向和横风向基底弯矩谱.图12为测压试验和测力试验的风洞试验模型图.

图11 控制风速为8 m/s基底弯矩谱

图12 风洞试验模型图
图13为由测压、测力以及气动弹性模型试验结果得到的峰值加速度响应值随折算风速的变化曲线.

图13 随风速变化的峰值加速度响应图
2.3.2测压与测力试验结果对比
整体来说,如图13所示,测力试验和测压试验得到的峰值加速度响应值是吻合的.测压试验结果处理采用惯性风荷载法,未将共振响应和背景响应分开考虑,将脉动响应作为整体计算,放大了脉动的作用;而测力试验结果进行加速度响应分析时,采用基底弯矩的阵风因子法,仅考虑了共振分量的作用,忽略了背景分量,结果偏小.因此可将测压计算中的峰值因子选取相对较小的值,将测力计算中的峰值因子选取相对较大的值.试验数据证明,在某些工况下,背景分量对加速度响应的影响是不应该忽略的,因此图13中测力结果较测压结果偏小.
从横风向加速度响应的对比结果看,图13(d)中,当折算风速达到14时,测力试验得到的横风向加速度响应值较测压结果大,这是由于模型的旋涡脱落频率与模型同天平系统整体的自振频率较为接近,使得在加速度响应计算时计入了模型与天平系统共振的那部分能量,导致结果偏大,见图14(a),前一个峰值对应的频率为模型的旋涡脱落频率,后一个峰值对应的频率为模型与天平系统共振所对应的频率.这进一步说明了测力天平试验中模型应保证轻质高强,且控制风速不宜过高,防止出现如图14(a)中两个峰值较为接近的情况,影响试验数据的准确性.针对这一现象,可采用文献[13]中所介绍的方法,消除模型共振的影响,见图14(b)以及图15,这里不再详述.
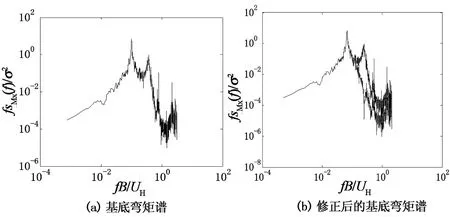
图14 控制风速15 m/s 90°风向角横风向基底弯矩谱
从顺风向的加速度响应的对比来看,测力和测压结果吻合程度没有横风向的好,这里参考图11可以得出,顺风向的基底弯矩谱在低频段没有突出的峰值出现,峰值段较宽且平缓,即旋涡脱落的能量分布较散,使计算共振分量时计算结果偏小,而横风向的基底弯矩谱中低频段出现突出的窄带峰值,能量集中,共振分量计算结果会较前者大一些.
图15 消除共振影响前后基底
2.3.33种试验方法结果对比
从图13中可以看出,不论是测力结果还是测压结果,考虑了气动阻尼后,结构的峰值加速度响应都有明显的减弱.
测压和测力试验在考虑气动阻尼作用下得到的峰值加速度与气动弹性模型试验结果十分接近,验证了气动弹性模型试验的正确性.
不考虑气动阻尼时,刚体模型试验得到的峰值加速度比气动弹性模型试验结果大很多,差值最大达到41%,对于横风向的峰值加速度,随着控制风速的不断提高,考虑气动阻尼的峰值加速度与不考虑气动阻尼的峰值加速度差值逐渐减小,甚至在90°风向角下出现考虑气动阻尼的峰值加速度值大于不考虑气动阻尼的峰值加速度,这说明当风速足够大时,会出现负值的气动阻尼,使响应值有增大的趋势,可见考虑气动耦合是十分有意义的.
在90°风向角下控制风速为15 m/s时,结构的顺风向峰值加速度气动弹性模型试验结果偏大,横风向结果偏小,这是前文提到的“拍”现象,导致结构横风向的部分能量转移到顺风向,造成结构顺风向的响应增大,横风向的响应减小.
3结论
本文自制了气动弹性模型,通过模拟结构的质量和刚度,测试出结构的动态响应,模拟高层建筑与风的相互作用过程,以及气动反馈效应,识别结构的动力特性以及对风振响应起重要作用的气动阻尼比,研究气动阻尼比随风速的变化规律.同时制作相同外形尺寸的刚性测压模型和测力模型进行了风洞试验研究,通过考虑气动阻尼的影响,验证气动弹性模型试验结果的正确性.得到了以下结论:
1)气动弹性模型风洞试验中,在进行动力特性测试时,由于结构X,Y方向自振频率接近,结构的响应衰减曲线出现了“拍”现象.在改进前人方法的基础上,根据阻尼是造成两个方向机械能损失的原因,通过将两个方向的响应幅值平方和开平方,得到了在零附近上下振动的理想的衰减曲线.而在气动阻尼识别过程中,当风速很大,且弱轴处于横风向振动时,横风向的部分能量会转移到顺风向上来,也会出现“拍”现象,为了解决这个问题,本文采用了滤波的方法,将横风向的能量去除,从而得到理想的衰减曲线.
2)在气动阻尼识别过程中,结构出现了涡激共振现象,并通过实验数据解释了当名义上的斯托罗哈数频率与结构的自振周期接近时,产生了涡激共振.另外还发现由于气动刚度的影响,涡激共振频率小于结构的自振频率.
3)在分析气动阻尼时,将响应时程数据进行NExT法处理以及IFFT计算,得到互相关函数,代替脉冲响应函数作为ARMA模型时序法的输入数据,得到总的阻尼比.为了减少噪声干扰,采用了改变模态阶数的方法,在模型的拟合曲线与测试曲线吻合得较好的前提下,找到与测得频率值接近的稳定频率值所对应的阻尼比作为最终结果.
4)从气动阻尼随风速的变化曲线图中可以看出,对于90°风向角的横风向,当风速足够大时,气动阻尼会出现负值,加剧结构的风振响应,高层建筑抗风设计应重视此问题.另外图10(d)反映出,90°风向角下顺风向气动阻尼比与折算风速的变化关系曲线在局部曲线段,在折算风速的某个变化区间,气动阻尼比也会出现图10(c)所示强风作用下,气动阻尼比随折算风速的增大而下降的特点.
5)从3种试验得到的峰值加速度响应值随折算风速的变化曲线中可以得出,考虑气动阻尼时的测压和测力结果得到的峰值加速度与气动弹性模型试验结果十分接近,验证了气动弹性模型试验的正确性.不考虑气动阻尼时,刚体模型试验得到的峰值加速度比气动弹性模型试验结果大很多,差值最大达到41%;而负气动阻尼,会加剧结构的动态响应,由此可见考虑高层建筑气动耦合效应是十分有意义的.
参考文献
[1]KAREEM A, GURLEY K. Damping in structures: its evaluation and treatment of uncertainty[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2): 131-157.
[2]VICKERY B J, STECKLEY A. Aerodynamic damping and vortex excitation on an oscillating prism in turbulent shear flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1): 121-140.
[3]KAREEM A. Fluctuating wind loads on buildings[J]. Journal of the Engineering Mechanics Division, 1982, 108(6): 1086-1102.
[4]全涌, 顾明. 超高层建筑通用气动弹性模型设计[J]. 同济大学学报: 自然科学版, 2001, 29(1): 112-116.
QUAN Yong, GU Ming. Design of super-high rise buildings’ global aeroelastic model[J]. Journal of Tongji University: Natural Sciences, 2001, 29(1): 112-116.(In Chinese)
[5]全涌. 超高层建筑横风向风荷载及响应研究[D]. 上海: 同济大学土木工程学院, 2002: 76-96.
QUAN Yong. Across-wind loads and response of super-high-rise buildings[D]. Shanghai: College of Civil Engineering, Tongji University, 2002: 76-96. (In Chinese)
[6]全涌, 顾明. 方形断面高层建筑的气动阻尼研究[J]. 工程力学, 2004, 21(1): 26-30.
QUAN Yong, GU Ming. Wind tunnel test study of aerodynamic damping of super highrise buildings[J]. Engineering Mechanics, 2004, 21(1): 26-30. (In Chinese)
[7]QUAN Y, GU M, TAMURA Y. Experimental evaluation of aerodynamic damping of square super high-rise buildings[J]. Wind & Structures, 2005, 8(5): 309-324.
[8]黄东梅, 朱乐东, 丁泉顺. 高层建筑气弹模型模态参数识别[J]. 振动工程学报, 2008, 21(3): 291-297.
HUANG Dong-mei, ZHU Le-dong, DING Quan-shun. Identification of modal parameters for a high-rise building aeroelastic model[J]. Journal of Vibration Engineering, 2008, 21(3): 291-297. (In Chinese)
[9]吴海洋, 梁枢果, 陈政清, 等. 强风下方截面高层建筑横风向气动阻尼比研究[J]. 工程力学, 2010,27(10): 96-103.
WU Hai-yang, LIANG Shu-guo, CHEN Zheng-qing,etal. Research on the aerodynamic damping ratios of square tall buildings in across-wind direction under strong wind[J]. Engineering Mechanics, 2010,27(10): 96-103. (In Chinese)
[10]金新阳, 王建, 王国砚. GB 50009-2012 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012: 220-226.
JIN Xin-yang, WANG Jian, WANG Guo-yan. GB 50009-2012 Load code for the design of building structures[S].Beijing: China Building Industry Press, 2012: 220-226. (In Chinese)
[11]王济, 胡晓. MATLAB在振动信号处理中的应用[M]. 北京: 中国水利水电出版社, 2006: 83-89.
WANG Ji, HU Xiao. The application of MATLAB in vibration signal processing[M]. Beijing: China Water Power Press, 2006: 83-89. (In Chinese)
[12]黄鹏, 顾明, 全涌. 高层建筑气动阻尼的实验研究[C]//第十二届全国结构风工程学术会议论文集. 西安, 2005: 359-364.
HUANG Peng, GU Ming, QUAN Yong. Wind tunnel test study of aerodynamic damping of highrise buildings[C]//Proceedings of 12th Structural Wind Engineering Conference. Xian, 2005: 359-364. (In Chinese)
[13]邹良浩, 梁枢果. 半刚性模型风洞试验荷载谱的处理方法[J]. 实验流体力学, 2007, 21(3): 76-81.
ZOU Liang-hao, LIANG Shu-guo. A method to evaluate wind force spectra of semi-rigid model in wind tunnel tests[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(3): 76-81. (In Chinese)
Experimental Study of Aeroelastic Effect on Tall Building
LI Qiu-sheng1,2†,CHEN Fan1
(1. College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China;2. Department of Architecture and Civil Engineering,City Univ of Hong Kong, Hong Kong999077, China)
Abstract:This paper studied the aeroelatic effect on tall buildings. An aeroelastic model was designed and manufactured for wind tunnel tests. With the time-history responses of the structure obtained from the aeroelastic model in the wind tunnel test, we could identify the structural dynamic characteristics by spectral analysis, and get the aerodynamic damping from the natural excitation technique method (NExT), the ARMA method, combined with a change in mode order, and then study the rules of aerodynamic damping changing with wind speeds. In a strong wind situation, filter technique was used to analyze the along-wind time-history acceleration response to eliminate the influence of the across-wind energy transfer. And vortex-excited resonance existed in the process of identifying the aerodynamic damping. The peak acceleration responses of the rigid models by pressure test and high-frequency-force-balance test, which considered the aerodynamic damping ratios, were very close to the results of the aeroelastic model test. The accuracy of the aeroelastic model test was verified. For the rigid models, irrespective of aerodynamic damping ratios, the peak acceleration responses were much larger than the results of the aeroelastic model test. The biggest difference was 41%. However, in some cases, the aerodynamic damping ratios increased the responses, and the necessity of considering the aerodynamic coupling effect on the wind-resistant design of flexible high-rise buildings has been verified.
Key words:tall buildings; aeroelastic model; wind tunnel test; dynamic characteristics; aerodynamic damping; peak acceleration
中图分类号:TU973.32
文献标识码:A
作者简介:李秋胜(1962-),男,湖南永州人,湖南大学教授,国家特聘专家,教育部长江学者†通讯联系人,E-mail:qifeideque@163.com
*收稿日期:2014-11-06基金项目:国家自然科学基金资助项目(51178179),National Natural Science Foundation of China(51178179) ; 国家自然科学重大项目(91215302)
文章编号:1674-2974(2016)01-0020-09
