在小学数学教学中渗透转化思想

葛斯贞

摘要：数学问题的解决过程，实际上是把未知的、较难的问题转化为自己比较熟悉的问题，从而解决该问题的一个过程。本文分析了数、图形、数形、式、问题之间的转化，旨在提高学生的解题效率。

关键词：小学数学教学 渗透 转化思想

著名数学家莫斯科大学教授C.A.雅洁卡娅曾说过：“解题就是把要解的题转化为已经解过的题。”转化是最常用的数学解题思想，它是指对于直接求解比较困难的问题，人们可以通过观察、分析、类比、联想等思维过程，选择恰当的数学方法进行变换，把原问题转化为一个新问题（或者相对来说，自己比较熟悉的问题），通过求解新问题，达到解决原问题的目的。

在数学教学中运用转化思想，能使计算、公式、数量关系化生为熟、化难为易、化繁为简、化曲为直。可见，在小学数学教学中，处处都渗透着转化思想。

下面，笔者结合实例，谈谈在小学数学教学中如何运用转化思想解决问题。

一、数之间的转化

有这样一道题目：“求0.125×0.875的积。”如果学生用小数乘法计算这道题目，那么算式比较繁琐，学生很容易出错。但是如果教师引导学生把小数乘法转化为分数乘法，问题就迎刃而解了，而且学生也不容易出错，大大提高了计算效率。

在小学分数、小数、百分数的计算中，数之间的相互转化，能够大大提高计算速度和准确率，所以在平时教学中，教师应重视在课堂教学中渗透转化思想。

二、图形之间的转化

在学生掌握了计算长方形和正方形面积的方法后，笔者开始教学生推导三角形的面积公式。

如在求“直角三角形的面积”时，笔者用两个形状相同的直角三角形拼成一个长方形，要求学生计算出一个三角形的面积，最后引导学生用“底（拼成的长方形的长）×高（拼成的长方形的宽）÷2”的公式计算出三角形的面积。

又如在求一般“三角形的面积”时，笔者用两个形状相同的三角形拼成一个平行四边形，然后通过割补的方法，把它变成一个长方形，能够同样得出“三角形面积=底×高÷2”。

再如在推导圆面积公式时，笔者把圆沿直径切成若干等份，拼成一个长方形，这个长方形的长就是圆周长的一半，即πr，拼成的长方形面积就是“r·πr=πr2”。

由此可知，在图形之间渗透转化思想，能使复杂的问题简单化，有助于学生解题。

三、数形之间的转化

在教学《异分母分数加减法》时，笔者发现学生很难理解为什么要先通分，而不是直接把分子与分子相加减，分母与分母相加减。为了解决学生的困惑，笔者用图形来表示两个分数，便于学生直观地了解，由于“单位1”的量不同，两个分数的分数单位不统一，同样各取一份出来，但数量是不一样的，所以不能相加减。如果要把两个分数相加减，只有把两个分数先通分，统一单位后才可以相加减，并且分数加减时分母不变。由于笔者把两个抽象的分数转化成图形之后，学生立刻能看出原因所在，容易接受异分母分数相加减，要先通分，化成同分母分数后，只要分子相加减，分母不变这一新知识。

由于题目中每个分母中的两个因数都相差3，如果把原式的分子、分母都乘以3，各项提取后，括号内的数拆成分数加减，从括号内第二项开始分别与后面一项相互抵消，直到剩下第一项和最后一项，这样计算就容易多了。如果按照常用的方法计算，先通分，再化成同分母分数相加，不仅计算繁琐，而且学生容易出错。在平时的教学中，教师可以先让学生通过一定的练习，感受到转化思想的优势，那么在今后的学习中，学生便会自觉地运用转化思想解决问题。

五、问题之间的转化

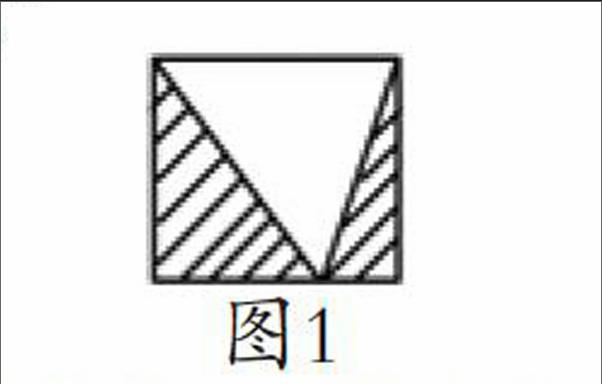
有这样一道题目：“图1是边长为1厘米的正方形，求阴影部分的面积。”

按照传统的解题思路，阴影部分由大、小两个三角形组成，要求这两个三角形的面积，必须分别找出它们的底和高，这就增加了解题的难度。

如果学生换一个角度去思考，不直接求阴影部分的面积，而是先求空白部分的面积，再从正方形面积中减去空白部分的面积，那么空白部分的三角形的底和高就是正方形的边长。

学生还可以再换一个角度去思考，空白部分的三角形的底和高是正方形的边长，空白部分的三角形面积就是正方形面积的一半，所以阴影部分的三角形面积就等于空白部分的三角形面积，也等于正方形面积的一半。

六、知识之间的转化

数学知识间的联系十分密切，学生掌握好知识间的联系，对他们学习数学影响甚大。如比、除法、分数这三者既有联系，又有区别。比的前项相当于除法中的被除数，又相当于分数中的分子，但比表示的是一种关系，除法表示一种运算，分数则表示一个数，所以比的结果虽然可用分数形式写，但当比的前项比后项大时，这个比的结果是不能写成分数形式的，即21∶16≠1。

转化思想的实质是揭示数学知识之间的联系，实现数学知识之间转化。除了简单的数学问题之外，很多数学问题都可通过转化得以解决。从这个意义上讲，解决数学问题就是从未知向已知转化的过程。数学中的转化思想比比皆是，如未知向已知转化，复杂问题向简单问题转化，新知识向旧知识转化，命题之间的转化、数与形的转化、空间向平面的转化、高维向低维的转化、多元向一元转化、高次向低次转化、超越式向代数式的转化、函数与方程的转化等，都是转化思想的体现。由此可见，转化思想是解决数学问题的根本思想。

在小学数学教学中，教师可以多引导学生运用转化思想来解决数学问题，提高学生的学习效率。

参考文献：

[1]刘长福.在小学数学“空间与图形”教学中渗透转化思想[J].科学咨询（教育科研），2014，（2）.

[2]张玉勤.转化思想在小学数学教学中的运用[J].学周刊，2014，（17）.

[3]蔡玉玲.浅谈转化思想在小学数学教学中的渗透[J].学周刊，2016，（4）.

[4]刘延革.在小学数学教学中渗透“转化思想方法”的策略[J].小学教学研究（教学版），2013，（8）.

（作者单位：浙江省绍兴市柯桥区稽东镇中心小学）endprint