惯性信息辅助的快速大视角图像匹配方法

王云舒，刘建业，曾庆化，刘 昇

（1. 南京航空航天大学 自动化学院南京 211106；2. 卫星通信与导航协同创新中心南京 211106；3. 中航工业洛阳电光设备研究所，洛阳 471009）

惯性信息辅助的快速大视角图像匹配方法

王云舒1,2，刘建业1,2，曾庆化1,2，刘 昇3

（1. 南京航空航天大学 自动化学院南京 211106；2. 卫星通信与导航协同创新中心南京 211106；3. 中航工业洛阳电光设备研究所，洛阳 471009）

大视角图像匹配算法的鲁棒性与实时性直接影响飞行器对远距离目标定位的性能。针对目前仿射不变图像匹配算法实时性较差的问题，提出一种惯性信息辅助的快速大视角图像匹配方法。该方法对现有的快速图像匹配算法进行改进，避免了构建高斯金字塔，提高了算法效率。然后利用机载惯性导航信息求解实时图与参考图之间的单应性矩阵，并对实时图进行模拟视角变换以此减小图像间视角差异，克服了现有的大视角图像匹配算法盲目多次的匹配计算，实现了大视角图像的快速匹配。实验结果表明，惯性信息辅助的大视角图像匹配算法与现有的快速仿射不变性匹配算法相比，匹配效率提高了至少2倍。

大视角图像；仿射不变性；惯性导航；图像匹配；目标定位

飞行器对远距离目标的精确定位对于飞行器导航及精确打击目标具有重要意义。对目标定位通常分为无地图定位与地图定位，无地图定位是指飞行器通过机载瞄准吊舱对目标进行测距测角，从而计算目标相对载机的相对位置信息，该方法在载机相对目标较远时定位误差较大；地图定位则是通机载吊舱拍摄到的目标图像（实时图）与已有的目标区域图像（基准图）进行匹配，依据匹配结果判定目标在目标区域中的准确位置，从而为精确制导武器提供必要的目标初始信息。因此，图像匹配算法的性能将直接影响目标定位的精度。

图像匹配算法中，基于局部特征的匹配算法例如SIFT、SURF算法因其对旋转、尺度变换、光照变化等都具有良好的鲁棒性而得到广泛的应用[1]。但SIFT、SURF等算法不具有仿射不变性，当飞行器拍摄的实时图（斜视）与基准图（俯视）之间有较大视角差异时（通常在50°以上），SIFT等算法性能不佳[2]。

目前在图像处理领域已有许多具有一定仿射不变性的匹配算法，能够对大视角图像进行匹配，一种是局部仿射不变的算法，如MSER算法[3]。此类算法是将存在未知仿射形变的局部区域转变为标准形状，以此消除仿射形变的影响，因此对视角变换较大的图像匹配效果仍不理想。Morel于 2009年提出了 ASIFT (Affine-SIFT)算法[4]，通过大量模拟待匹配图像的视角变换并依次匹配，找到匹配点最多的几组图像，然后将所有匹配点映射至原匹配图上，实现了大视角下的图像匹配，但其效率较低，难以在飞行器上实时应用。之后有学者为提高 ASIFT算法的效率进行了大量研究，主要分为两个方向，一是使用快速的图像匹配算法代替SIFT算法，例如AORB(Affine Oriented FAST and Rotated BRIEF)算法[5]和ASURF(Affine- SURF)算法[6]；二是改进模拟视角变换的采样策略，例如使用粒子群优化算法[7]、正交试验法[8]等，这些方法虽然提高了ASIFT算法的效率，但由于事先不知道图像间的视角变化关系，仍然需要进行多次视角变换以及匹配，实时性仍然有待提升。

由于惯性信息的获取不受外界影响，可以利用机载惯性信息求解图像间的视角变换关系[9]。为此，论文提出了惯性信息辅助的快速大视角图像匹配算法，利用载机的惯性信息求解待匹配图像间单应性矩阵，克服了现有算法盲目遍历的缺点，大大减少了视角模拟变换次数及图像匹配次数。然后对快速图像匹配算法ORB算法[10]进行改进，使用DAISY描述符[11]对特征点进行描述，由于DAISY描述符本身具有尺度不变性，避免了ORB算法中对多层图像特征检测的步骤，进一步提高了算法效率，并采用灰度矩心方法进行特征点主方向度量，使算法具备了旋转不变性。实验对比了载机惯性信息辅助的大视角图像匹配算法与经典仿射不变性图像匹配算法的匹配效果及计算速度，本文提出方法在保证匹配效果的同时大大提高了算法效率。

1 惯性信息辅助的大视角图像匹配算法

当飞行器距离目标较远时，载机拍摄的实时图与参考图之间的视角差异通常在50°以上，如图1所示。

传统的特征匹配方法如 SIFT算法无法对上述图像进行匹配，而MSER等具有局部仿射不变性的算法匹配效果也不理想，ASIFT算法虽然能实现大视角图像的匹配，但耗时较多，无法在飞行器上实时应用。为此，本文提出了惯性信息辅助的快速大视角图像匹配算法解决该问题。

图1 视角变换较大的参考图与实时图Fig 1 Refer image and the real image with large viewpoint change

1.1 坐标系建立

惯性信息辅助的快速大视角图像匹配示意图如图2所示。目标T位于地理坐标系Og-XgOgYg中的XgOgYg平面上，地理坐标系Og-XgYgZg为东北天坐标系，参考图一般由卫星地图提供或高空无人侦察机事先拍摄，拍摄参考图的相机用相机坐标系表示，参考图通常为俯视图，因此该相机坐标系的光轴Oc′Zc′通常垂直于地面。飞行器的机体坐标系Ob-XbYbZb为右前上坐标系，飞行器携带的光学相机用相机坐标系Oc-XcYcZc表示。

图2 惯性信息辅助的大视角图像匹配示意图Fig.2 Schematic of large viewpoint image matching aided by inertial information

本文利用机载惯性信息求解实时图与参考图间的单应性矩阵，对实时图进行视角变换，避免了多次盲目的视角变换与匹配，提高计算效率。

1.2 坐标系转换关系

通过对机载惯性信息解算，可以得到载机的航向角ψ、俯仰角θ和滚转角γ，因此可以得到地理坐标系（与导航系重合）到机体坐标系的变换矩阵：

机载相机通常是固连在机载二轴稳定平台上的，即平台有方位和俯仰两轴的运动。初始状态下，相机的光轴方向即Zc轴与机体系的Yb轴方向相同，Xc轴与Xb轴方向相同，Yc轴与Zb轴方向相反。定义Zc轴在水平面上的投影与Yb轴在水平面上的投影间的夹角为平台方位角为α，初始值为0°，顺时针方向为正，定义域为0°～360°，定义相机绕Xc轴转动产生的Yc轴与Zb轴反方向之间的夹角为平台俯仰角β，初始值为0°，向下为正，定义域为0°～180°。为简化模型，忽略相机系与机体系之间的平移关系，则相机系到机体系的变换矩阵可以表示为

另外，由于拍摄参考图的相机光轴几乎垂直于地面，所以认为Zc′垂直地面向下，Xc′与Xg方向相同，Yc′与Yc方向相反，所以有：

结合式(1)～(3)，可以得到两个相机坐标系之间的转换关系：

由此得到了图2中四个坐标系之间的相互转换关系，之后将建立描述两个相机间视角变换的单应性矩阵，然后通过本节分析的坐标转换关系实现惯性信息辅助的视角变换。

1.3 惯性信息辅助的视角变换

假设目标点p在XgOgYg平面上，根据相机成像原理可知，对于实时图与参考图中的同一目标点p，存在如下关系：

联立式(7)和式(8)，可以得到：

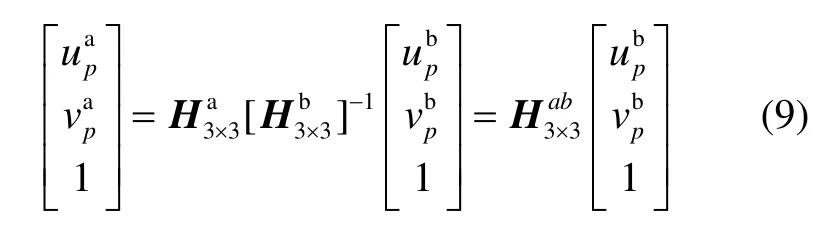
将式(10)带入式(9)，就可以求出实时图中坐标到参考图中坐标的转换关系，再通过插值即可实现实时图到参考图的视角变换，得到模拟视角变换后的实时图，如图3所示。

用模拟视角变换后的实时图与参考图匹配能够获得更多的匹配点以及更高的正确率。

图3 实时图和视角变换后的实时图Fig.3 Real image and the real image after viewpoint change

2 快速图像匹配算法

获得模拟视角变换后的实时图，就可以采用快速图像匹配算法进行特征匹配。ORB算法是一种快速图像匹配算法，该算法使用FAST算子[12]提取特征点，用BRIEF描述符[13]对特征点进行描述，BRIEF描述符的计算速度较快，但是不具备尺度不变性与旋转不变性，ORB算法使用灰度矩心法为每个特征点构建主方向使其具有旋转不变性，建立高斯金字塔模拟图像尺度变换使其具有尺度不变性。为进一步提高算法效率，本文对ORB算法进行了改进，使用DAISY描述符代替BRIEF描述符，DAISY描述符本身具有尺度不变性，避免了 ORB算法中构建高斯金字塔的过程，提高了特征检测的效率，但与 BRIEF描述符类似，DAISY描述符没有主方向，因此不具备旋转不变性。为此，本文采用灰度矩心方法为FAST特征点构建主方向。图像角点区域的灰度矩定义为

式中，I(u,v)是图像中特征点(u,v)处的灰度值，p、q决定了灰度矩的阶数。灰度矩心可由三个不同的灰度矩m00、m01和m10来表示：

然后可以构造角点中心到矩心的向量，因此角点的主方向为

将提取的角点主方向用于特征描述符DAISY，即可获得旋转不变的DAISY描述符。DAISY描述符的结构如图4所示，围绕着中心点有三层同心圆，每层同心圆上有8个采样点，以45°为间隔，每层同心圆环的采样点具有相同的高斯尺度值，DAISY描述符将原始图像的若干个梯度方向与尺度不一的高斯滤波函数进行卷积，每个采样点上卷积核的大小与该采样点到同心圆中心的距离成正比。由于高斯滤波函数具有可分离性，因此该方法具有较高的效率，并且这种圆环结构使 DAISY描述符对于图像的仿射变化和光照差异都有较好的鲁棒性。

图4 DAISY描述符结构Fig.4 Structure of DAISY descriptor

下面将构建基于有向FAST特征点的DAISY描述符：对任意一个FAST特征点(u,v)计算其8个方向的梯度：

式中，o表示梯度的方向，o=1,2,…,8。然后用高斯尺度值为∑的高斯核G∑对梯度图像Go(u,v)进行高斯卷积：

对每一个特征点都可以找到一个长度为8的向量来表示局部梯度方向直方图，记为：

由此可以得到DAISY描述符为：

式中：N表示描述符的层数，通常为3；di(u,v,Rj)表示以特征点(u,v)为中心的第j个同心圆上第i个采样点的坐标，例如表示以特征点(u,v)为中心的第1个同心圆上第一个采样点的局部梯度直方图。

对于一个有主方向的特征点，将每个同心圆上的第1个采样点定义在主方向上，两个特征点匹配时，先将主方向旋转到一致的方向，然后求解两个特征点描述符间的欧式距离，从而使得匹配算法具有旋转不变性。

3 算法流程

惯性信息辅助的大视角图像匹配算法流程如图 5所示，主要分为以下步骤：

1）载机获取实时图，并读取此时刻载机惯性信息；

3）通过单应性矩阵对实时图视角变换，减小实时图与参考图间的视角差异后，使用快速图像匹配算法对两幅图进行匹配，得到初始匹配结果；

4）使用RANSAC（随机采用一致性）算法剔除匹配结果中的错误匹配点，输出最终匹配结果。

图5 惯性信息辅助的快速大视角图像匹配算法流程示意Fig.5 Schematic of fast matching method for large viewpoint image aided by inertial information

4 实验验证

实验对本文提出算法、SIFT算法、MSER算法、ASIFT算法以及AORB算法在实时图与参考图视角差异较大情况下的匹配性能进行比较。实验中 SIFT与MSER算法使用基于Matlab的VLFeat开源图像算法库中的相应算法，ASIFT使用作者在网站上提供的代码，所有算法的参数都使用程序默认的参数。特征匹配策略采用最近邻/次近邻比率算法(Nearest Neighbor with Distance Ratio)算法，算法中最邻近比率取0.7。

本文实验环境为32位Windows7操作系统，安装内存4G，Intel(R) Pentium(R) G2020处理器(2.90GHz)，实验软件为Matlab(R2012a)，由于VLFeat中的SIFT、MSER等算法的核心代码都是在Matlab下调用C文件实现的，为使对比环境一致，本文算法的核心代码也用C语言实现，然后通过混合编程使用Matlab调用。

实验对算法进行了仿真测试，使用卫星图像作为参考图，参考图分辨率为1027×702，设置飞行器在该区域上空飞行的航迹，飞行高度为 800 m，并在飞行到点1、2、3时分别对目标进行拍摄获取实时图，实时图分辨率均为200×120，如图6所示，拍摄图像时载机惯性信息、目标相对载机距离以及机载相机姿态信息如表1所示，目标相对距离与载机位置变化导致机载相机姿态变化，从而引起图像视角差异的变化。

使用SIFT、MSER、ASIFT、AORB算法和本文提出算法分别对上述图像进行匹配测试，获得匹配点后使用 RANSAC算法剔除错误点，得到正确匹配点数目以及正确率，每幅图像所获得的正确匹配点数与正确匹配率如图7所示。

图6 实验参考图与不同载机位姿获取的实时图Fig.6 Reference image and real-time images when with different poses and locations of UAV

表1 拍摄实时图时载机惯性信息及机载相机姿态Tab. 1 Inertial information and camera pose of real images

可以看出，不具有仿射不变性的匹配算法 SIFT仅在视角差异为50°时获得了3对正确匹配点，正确匹配率为60%，视角差异增大后SIFT无法获得正确匹配点。而本文提出算法与其他具有仿射不变性的匹配算法一样，能够对大视角图像进行匹配，其中，ASIFT算法性能最佳，因为SIFT算法的鲁棒性最佳，通过大量设置采样点模拟视角变换，保留了多个视角变换下的匹配点，因此能够获得最多的匹配点与最高的匹配正确率。AORB采用了与ASIFT相同的视角模拟方法，但 ORB算法为了提高计算效率牺牲了部分鲁棒性；MSER算法仅对部分区域进行归一化，不具有全仿射不变性，因此获得的匹配点较少；本文提出算法获得的匹配点与AORB算法相近，优于MSER算法，并且匹配正确率与ASIFT算法相近。

图7 各图像匹配算法效果对比Fig.7 Effect comparison of various images’ matching methods

为验证本文提出算法的计算速度，本文对大视角图像匹配算法进行测试，用ASIFT、AORB、MSER和本文算法分别对三组图像进行了10次匹配，并对比了30次匹配的平均耗时，每个算法的耗时由特征检测耗时(detection)，特征描述耗时(description)，特征匹配耗时(match)和其他耗时(others)组成，ASIFT、AORB中的其他耗时主要指模拟图像视角变换的时间，MSER算法中的其他耗时主要指检测极大值稳定区域及归一化的时间，本文算法中的其他耗时主要指解算惯性信息并模拟视角变换的时间，对比结果如图8所示。

可以看出，本文提出算法和MSER算法的耗时明显小于ASIFT和AORB，MSER算法仅对部分极大值稳定区域进行了归一化处理，而本文提出算法对图像进行了一次模拟视角变换，所以其他部分的耗时比MSER算法多；特征提取和描述方面，MSER算法对归一化的极大值稳定区域进行SIFT特征提取与描述，而本文算法通过对 ORB算法改进，这部分的计算速度优于MSER算法；特征匹配耗时方面，由于MSER算法仅对归一化的区域进行了特征检测，因此获得的特征点比本文算法少，所以特征匹配耗时较少。

图8 各图像匹配算法计算时间对比Fig.8 Calculation time of each image’s matching method

为了进一步对比各算法的计算效率，用每幅图像的平均匹配时间除以每幅图像平均获得的匹配点数得到每个特征点的平均计算用时，对比结果如表2所示。从表中可知，虽然MSER算法与本文算法总时间相当，但获得的匹配点较少，所以平均每点用时较多。该指标同时考虑了算法匹配效果及匹配效率，更好地反映了匹配算法性能，本文算法平均每点的计算速度是 MSER的2.02倍，是ASIFT的6.34倍，是AORB的5.77倍。

表2 各算法平均每点用时对比Fig.2 Time/point of each method

5 结 论

本文提出了一种惯性信息辅助的大视角图像匹配算法，首先对 ORB快速图像匹配算法进行改进，提高了计算效率，然后利用载机惯性信息，通过坐标转换构建单应性矩阵，求解视角模拟变换参数，从而避免了多次盲目的视角模拟变换及匹配。实验通过模拟飞行中拍摄的大视角图像对本文提出算法进行验证。实验结果表明，惯性信息辅助的大视角图像匹配算法相比现有的快速仿射不变匹配算法，可对大视角下的图像进行有效匹配，对飞行器远距离目标定位有重要的意义，同时本算法相比现有的快速仿射不变匹配算法，计算效率提高了至少2倍。

（References）：

[1] 陈方, 熊智, 许允喜, 等. 惯性组合导航系统中的快速景象匹配算法研究[J]. 宇航学报, 2009, 30(6): 2308-2316. Chen Fang, Xiong Zhi, Xu Yun-xi, et al. Research on the fast scene matching algorithm in the inertial integrated navigation system[J]. Journal of Astronautics, 2009, 30(6): 2308-2316.

[2] 刘立, 詹茵茵, 罗扬, 等. 尺度不变特征变换算子综[J].中国图象图形学报, 2013, 08: 885-892. Liu Li, Zhan Yin-yin, Luo Yang, et al. Summarization of the scale invariant feature transform[J]. Journal of Image and Graphics, 2013, 08: 885-892.

[3] Matas J, Chum O, Urban M, et al. Robust wide-baseline stereo from maximally stable extremal regions[J]. Image & Vision Computing, 2004, 22(10): 761-767.

[4] Morel J M, Yu G. ASIFT: A new framework for fully affine invariant image comparison[J]. Siam Journal on Imaging Sciences, 2009, 2(2): 438-469.

[5] 侯毅, 周石琳, 雷琳, 等. 基于ORB的快速完全仿射不变图像匹配[J]. 计算机工程与科学, 2014, 36(2): 303-310. Hou Yi, Zhou Shi-lin, Lei Lin, et al. Fast fully affine invariant image matching based on ORB[J]. Computer Engineering and Science, 2014, 36(2): 303-310.

[6] Lin C, Liu J, Cao L. Image matching by affine speed-up robust features[C]//Proceedings of SPIE - The International Society for Optical Engineering. 2011, 8004: 80040G-80040G5.

[7] 蔡国榕, 李绍滋, 吴云东, 等. 一种透视不变的图像匹配算法[J]. 自动化学报, 2013, 39(7): 1053-1061. Cai Guo-rong, Li Shao-zi, Wu Yun-dong, et al. A perspective invariant image matching algorithm[J]. Acta Automatica Sinica, 2013, 39(7): 1053-1061.

[8] Liu W, Wang Y, Chen J, et al. A completely affine invariant image-matching method based on perspective projection[J]. Machine Vision & Applications, 2012, 23(2): 231-242.

[9] 夏琳琳, 于金鑫, 初妍, 等. 小倾角下空间后方交会算法辅助的 SINS/GPS姿态位置解算[J]. 中国惯性技术学报, 2015(3): 350-355. Xia Lin-lin, Yu Jin-xin, Chu Yan, et al. Attitude and position calculations for SINS/GPS aided by space resection of aeronautic single-image under small inclination angles[J]. Journal of Chinese Inertial Technology, 2015(3): 350-355.

[10] Rublee E, Rabaud V, Konolige K, et al. ORB: An efficient alternative to SIFT or SURF[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 2564-2571.

[11] Engin T, Vincent L, Pascal F. DAISY: an efficient dense descriptor applied to wide-baseline stereo[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 32(5): 815-30.

[12] Rosten E, Porter R, Drummond T. Faster and better: A machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 32(1): 105-119.

[13] Calonder M, Lepetit V, Strecha C, et al. BRIEF: Binary robust independent elementary features[C]//European Conference on Computer Vision. Springer-Verlag, 2010: 778-792.

Fast matching method for large viewpoint images aided by inertial information

WANG Yun-shu1,2, LIU Jian-ye1,2, ZENG Qing-hua1,2, LIU Sheng3
(1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China; 2. Satellite Communication and Navigation Collaborative Innovation Center, Nanjing 211106, China; 3. AVIC Luoyang Electro-optical Equipment Research Institute, Luoyang 471009, China)

The robustness and efficiency of large viewpoint image’s matching method immediately influence the performance of target location. Aiming at low efficiency of the affine invariant matching method, a fast matching method for large-viewpoint images aided by inertial information is proposed. The existing fast matching method is improved by the proposed method, which avoids building a Gaussian pyramid and improves the algorithm efficiency. Then the onboard inertial information is used to calculate the homography matrix between real-time image and reference image. The homography matrix is used to transform the real-time image so that the viewpoint change can be decreased. The blindness and quantity of the existing affine invariant matching methods are overcome. Experiment results show that the efficiency of the proposed method is improved by at least 2 times compared with the existing fast affine invariant matching methods.

large viewpoint image; affine invariant; inertial navigation; image matching; target location

TP391

：A

2016-05-03；

：2016-07-29

国家自然科学基金项目（61533008，61328301）；江苏省普通高校研究生科研创新计划项目（KYLX15_0277）；中央高校基本科研业务费专项资金资助（NS2014092）

王云舒（1990—），男，博士研究生，主要研究方向为图像匹配及惯性/视觉导航技术等。E-mail: wangys@nuaa.edu.cn

联 系 人：刘建业（1957—），男，教授，博士生导师。E-mail: ljyac@nuaa.edu.cn

1005-6734(2016)04-0504-07

10.13695/j.cnki.12-1222/o3.2016.04.015