基于AKAZE的BOLD掩码描述符的匹配算法的研究
2020-06-16邢长征李思慧
邢长征 李思慧
(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)
0 引 言
局部特征匹配算法是图像拼接[1-3]、SLAM[4-5]等重要的组成部分。局部特征匹配算法首先需要构建尺度空间,以满足匹配算法具有尺度不变性。尺度空间的构建方式主要有两种:(1) 高斯核函数与灰度图像卷积得到;(2) 利用非线性滤波函数构建。
利用高斯核函数构建尺度空间的匹配算法有:SIFT算法[6]、SURF算法[7]、ORB算法[8]等。这类算法具有较好的鲁棒性,匹配速度也比较快,但是高斯核函数卷积操作会致使图像的边缘信息丢失,严重影响特征点和描述符的稳定性。利用非线性滤波函数构建的尺度空间算法主要有:KAZE算法[9],AKZAE算法[10]等。非线性滤波函数构建的尺度空间可以更好地保护图像边缘处的信息,增加了匹配算法的鲁棒性。KAZE算法的特征点检测和描述符均借鉴SURF算法,但KAZE算法的鲁棒性较SURF算法更强,足以证明非线性尺度空间的优越性。鉴于非线性尺度空间的优越性,许多研究者在KAZE算法和AKZAE算法的基础上提出创新。文献[11]提出KAZE算法与FREAK描述符相结合的算法,虽增加KAZE算法的匹配算法,但是降低了算法的鲁棒性。针对KAZE算法匹配速度较慢等问题,文献[12]提出32维圆形M-SURF描述符,通过余弦相似性判断不同描述符的相似性,虽增加了匹配速度,但造成匹配鲁棒性严重下降。文献[13]提出把灰度图像替换为颜色不变空间,以增加AKAZE算法的鲁棒性,虽算法的鲁棒性得到增加,但匹配算法速度下降。文献[14]提出对AKAZE算法描述符进行更改,使用三元组LATCH描述符替代MLDB描述符,以增加AKAZE算法的匹配算法,但LATCH描述符[15]需要借助机器学习算法寻找最佳三元组像素块,故本身不具有良好的移植性。
综上所述,现有的改进AKAZE算法增加鲁棒性同时速度下降严重,增加匹配速度的同时鲁棒性下降严重。针对这一问题,本文提出一种BOLD掩码[19]的AKAZE算法,对采样区域旋转20度得到掩码采样区域并建立MLDB描述符,通过掩码区域MLBD描述符与采样区域MLDB做异或得到BOLD掩码,最后利用汉明距离衡量不同描述符的相似性。
1 AKAZE算法
1.1 非线性金字塔搭建
非线性扩散滤波算法主要是将灰度图像L在不同尺度上变化表示为流动函数的扩散过程,可用非线性偏微分方程表示为:

(1)
式中:L表示图像灰度信息;div表示流动函数的扩散;▽表示图像的梯度;c(x,y,t)表示传导函数。
c(x,y,t)=g(|▽Lσ(x,y,t)|)
(2)
式中:t为尺度参数;▽Lσ表示灰度图像L经过高斯滤波后的梯度图像。g(·)函数表示为:
(3)
式中:k为控制扩散度的对比因子。
在AKAZE算法基础上提出FED算法[16],解非线性扩散滤波函数中的偏微分方程式。FED算法可表示为:
Li+1,j+1=(I+τjA(Li))Li+1j=0,1,…,n-1
(4)
式中:I表示单位矩阵;A(Li)为图像Li的传导矩阵;n表示显性扩散步数;τj表示对应步长。
(5)
式中:τmax为最大迭代步长。单个FED算法周期的停止时间θn为:
(6)
在非线性尺度空间的组和层,用o和s来表示,则对应的尺度参数可以表示为:
σi(o,s)=σ02o+s/So∈{0,1,…,O-1}
s∈{0,2,…,S-1}i∈{0,2,…,O×S-1}
(7)
式中:σ0为初始尺度参数;O×S表示金字塔共有的层数。非线性尺度空间的尺度参数σ转换到时间单位中,映射关系可表示为:
(8)
式中:ti表示非线性金字塔的进化时间。
1.2 特征点检测
金字塔上寻找极大值从而确定特征点:
(9)
式中:σi为尺度因子初始值;Lxx为x方向的2阶导数,Lxy和Lyy类似。对于每一个经过Hessian矩阵归一化的像素点,将其与金字塔相邻尺度中σi×σi区域以及本身所在尺度σi×σi区域的像素点的大小比较,像素值最大值时为特征点。
定位到特征点位置后,以特征点为中心,画出半径为σi的圆分为6个扇形,计算每个扇形内所有像素点在横纵方向一阶导数的高斯加权值,高斯加权值最大方向为特征点主方向θ。
2 BOLD-MLDB描述符建立
在非线性尺度空间中提取了特征点并建立了特征点的主方向后,建立MLDB描述符进行匹配。本节提出BOLD-MLDB描述符,旨在增强AKAZE算法的鲁棒性。具体构建方式如下:
第一步以特征点为中心选取合适的采样区域P构建MLDB描述符[17],将采样区域P划分为n×n个网格。计算n×n单个网格内像所有像素值的平均值,表示为:
(10)
式中:I(k)为灰度图像的像素值;m是每个划分网格内的像素点的个数;i表示为采样区域一共被划分网格的数量。
第二步计算每个网格内像素点在x和y方向上的梯度,根据每个网格平均像素值和网格像素的梯度值进行编码,可表示为:
Func(·)={Funcintensity(i),Funcdx(i),Funcdy(i)}
(11)
式中:Funcintensity(i)=Iavg(i),Funcdx(i)=Gradientx(i)=dx,Funcdy(i)=Gradienty(i)=dy。
第三步由式(10)可得,构建出LDB描述符每一对网格比较得到的二进制位3位,可用公式表示为:

(12)
则MLDB描述符可表示为:
(13)
本文中MLDB描述符大小为256 bit。
第四步采样区域P以主方向θ为基准,旋转20度得到掩码采样区域P′,并建立掩码采样区域P′的MLDB描述符,如图1所示。

图1 M-LDB描述符构建

(14)
本文采样区域P的MLDB描述符为256 bit,则它的BOLD码同为256 bit,从而得到BOLD-MLDB描述符大小为512 bit。
3 描述符匹配
判断两个特征点描述符是否为同一对,SIFT算法计算不同描述符的欧式距离,AKAZE算法计算MLDB描述符的汉明距离。BOLD-MLDB描述符是由MLDB描述符和BOLD码组成,BOLD码表示为MLDB描述符的稳定性,因此不能单纯地计算描述符的汉明距离。若有两幅待匹配图像IR和IL,则fL表示IL特征点的MLDB描述符,mL表示BOLD码;fR表示IR特征点的MLDB描述符,mR表示BOLD码。计算BOLD-MLDB描述符距离可表示为:
(15)
式中:D表示为二进制描述符的维数。
4 实 验
4.1 实验过程
本文提出BOLD-AKAZE算法旨在增加AKAZE算法的鲁棒性,故选择AKAZE算法、SIFT算法和ORB算法与本文算法在Oxford数据集中具有模糊变换、放射性变换、JPG压缩变换和尺度变换的图像组进行对比实验,测试不同匹配算法匹配正确率和匹配算法的速度。AKAZE算法描述符为486 bit,ORB算法的描述符维度为256 bit,SIFT算法描述符的维度为126维;本文算法的M-LDB描述符为256 bit,BOLD掩码的描述符为256 bit,故BOLD-MLDB描述符为512 bit。测试图像如图3所示,每组测试数据共有6幅图像,第1幅图像为基准图像,其他图像为目标图像。
本文实验平台为个人笔记本,CPU主频为2.4 GHz、内存为8 GB,开发环境为VS2013+Opencv3.10。

(a) Bike图像(1/6) (b) Bike图像(6/6)

(c) UBC图像(1/6) (d) UBC图像(6/6)

(e) Wall图像(1/6) (f) Wall图像(6/6)

(g) Boat图像(1/6) (h) Boat图像(6/6)
4.2 实验结果
ORB算法利用FAST算法检测特征点,速度较快,而且BRIEF描述符仅通过比较两两像素的大小建立256 bit的二进制描述符,故匹配速度最快。AKAZE算法需要利用FED算法迭代解非线性函数,所需的时间较长;MLDB描述符需要计算梯度信息,且描述符的维度为486 bit,故匹配速度不及ORB算法。SIFT算法描述符为128维浮点型,需计算欧式距判断不同描述符的相似性,故匹配速度最慢。本文所提的BOLD-MLDB描述符的维度是512 bit,比传统的AKAZE算法描述符维度高,故匹配速度不及AKAZE。如表1所示,ORB算法、SIFT算法、AKAZE算法和本文算法的匹配速度排序为:ORB算法、AKAZE算法、本文算法、SIFT算法。

表1 匹配时间 s
ORB算法的尺度空间使用高斯核函数卷积得到,使得尺度空间中不同层的图像边缘信息丢失,影响了特征点和描述符的鲁棒性,而且ROB算法使用的FREAK描述符[18]构造简单,代表的局部信息较少,故ORB算法的匹配正确率最低。SIFT算法虽也使用高斯核函数构造尺度空间,但是SIFT描述符利用采样区域梯度信息建立128维描述符,描述信息量较大,鲁棒性较强,故匹配正确率超过ORB算法。AKAZE算法利用非线性滤波函数构造非线性尺度空间,可更好地保护图像边缘信息,保证了描述符和特征点的稳定性。而且MLDB描述符不仅由像素块强度编码得到,还引入像素块梯度信息,增加了描述符的可分辨性,故AKAZE算法的匹配正确率高于SIFT算法。本文所提算法在AKAZE算法基础上提出了BOLD-MLDB掩码,BOLD-MLDB掩码与MLDB描述符相结合,有效增加了描述符的鲁棒性,故BOLD-AKAZE算法的正确匹配率高于KAZE算法。
各算法对图2图像进行测试得到的匹配正确率柱状图如图3所示。对于Bike组具有模糊变换的图像,本文算法具有较好的鲁棒性,匹配正确率远优于ORB算法和SIFT算法,相较于AKAZE算法匹配正确率也有一定的提高。对于UBC组具有JPG压缩变换的图像,各算法的稳定性均很好,但本文算法的匹配正确率最佳。对于Wall组具有放射变换的图像,SIFT算法、ORB算法、AKAZE算法随着图像变换程度的加大,匹配正确率迅速下降,但是本文算法的匹配正确率下降速度缓慢。对于Boat组具有尺度变换的图像,各算法的匹配正确率均在下降,但当待匹配图像变换最大时,本文算法的匹配正确率仍高于30%。
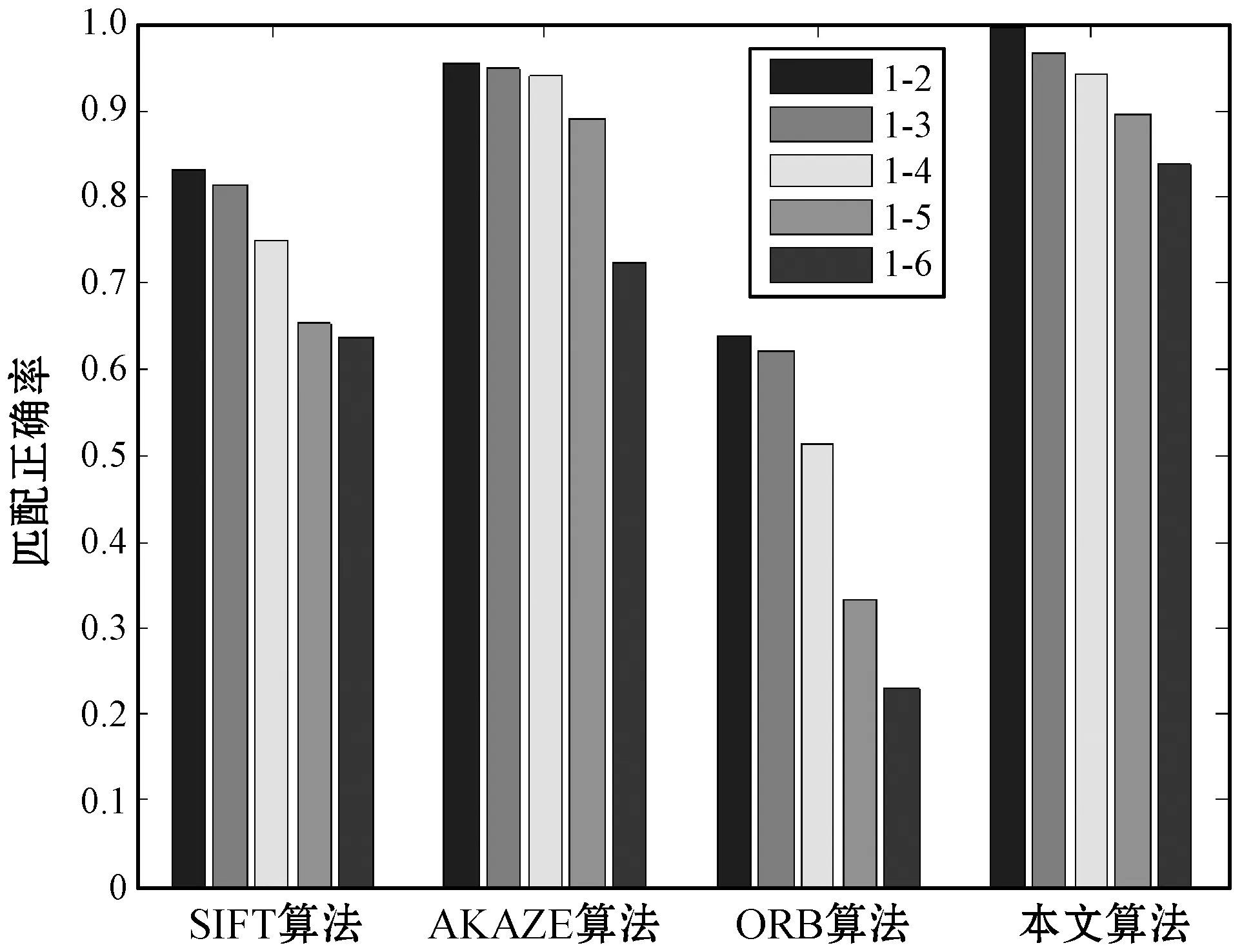
(a) Bike图像匹配正确率
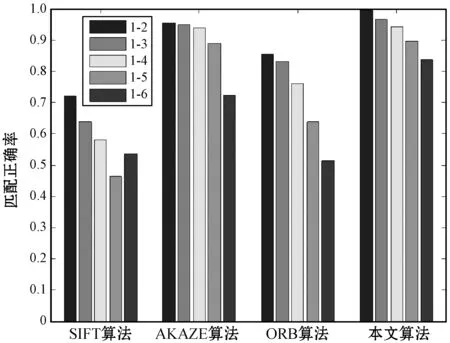
(b) UBC图像匹配正确率

(c) Wall图像匹配正确率

(d) Boat图像匹配正确率
5 结 语
针对现有AKAZE改进算法鲁棒性和匹配速度不佳的问题,本文提出一种BOLD掩码AKAZE算法。首先以特征点采样区域建立MLDB描述符;然后把采样区域旋转20度作为掩码采样区域建立MLDB描述符,并把掩码采样区域MLDB描述符与采样区域MLDB描述符做异或,得到BOLD掩码描述符;最后使用汉明距离衡量不同描述符的相似性。实验表明:本文算法的鲁棒性相较AKAZE算法有巨大的提升,匹配速度虽有减慢,但也仅是SIFT算法匹配时间的50%左右。综上所述,本文算法可应用于对鲁棒性要求较高且匹配速度较快的领域。
