Cantor集的自相似子集的压缩系数的讨论

曾 莹

(湖北工业大学 理学院 ，湖北 武汉430068)

Cantor集的自相似子集的压缩系数的讨论

曾 莹

(湖北工业大学 理学院 ，湖北 武汉430068)

许多分形都是由一些与整体以某种方式相似的部分所组成的，而对称Cantor集更是具有自相似性的一个典型而且非常重要的分形几何，在原有对称Cantor集自相似性性质的基础上对对称Cantor集的自相似子集的压缩系数的若干性质做进一步的探讨.

IFS吸引子；λ-Cantor集；压缩系数

对称Cantor集具有自相似性，本文将对对称Cantor集的自相似子集的压缩系数的若干性质做进一步的讨论.在本文中，我们约定R表示实数集，N表示自然数集，Q表示有理数集.

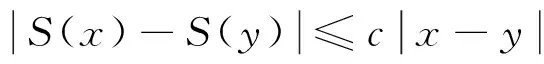
我们把一个有限的压缩映射族{S1,S2,…,Sm},(m≥2),称为一个迭代函数系(IteratedFunctionSystem)，简称IFS；称D的非空紧子集F为IFS的吸引子(或者称为不变集),若F满足下面的方程

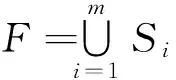
Hutchinson[1]与1981年证明了一个IFS有唯一的一个吸引子.通常吸引子是一个分形[2～6].

1 预备知识

下面给出Hausdorff度量，用D表示D的全部非空紧子集组成的集类.对于A⊆D我们称所有与A距离不大于δ的D上的点组成的集为A的δ平行体，即

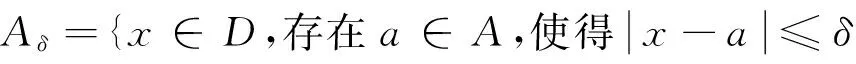
设A,B是D的两个子集，定义A,B的Hausdorff度量为

d(A,B)=inf{δ:A⊂Bδ且B⊂Aδ}.

引理1[1](D，d)是完备度量空间,d是D上的完备度量，即D中的每个柯西列都收敛到D中的一个元素.

下面给出IFS上的一个基本结论.

设{S1,S2,…,Sm}是D⊂Rn上的迭代函数系，满足

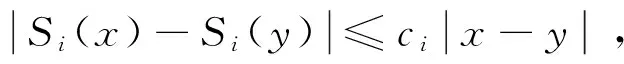
(1)

对E∈D,定义Hutchinson算子

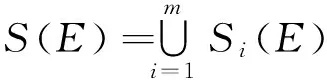
且记Sk为S的k次迭代,S1(E)=S(E),且对k≥2,Sk(E)=S(Sk-1(E)).

引理2 对于迭代函数系(1)，存在唯一的非空紧集F，满足:

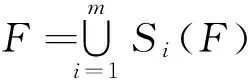
(2)

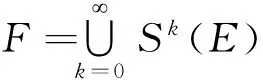
证明 显然Hutchinson算子S是D到自身的映射.如果A,B∈D，则

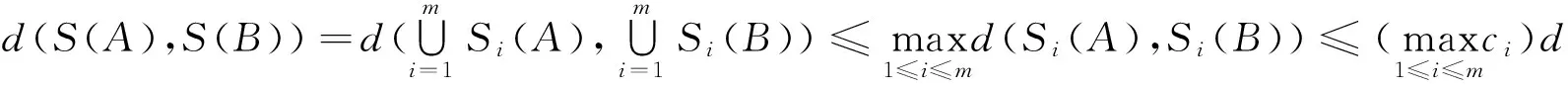
(3)

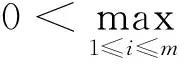
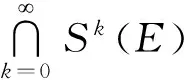
引理3 若a是IFS中某个映射Sj的不动点，则a∈F.

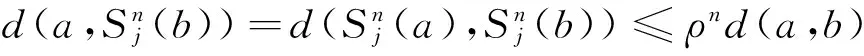
从而当n→时，，即，又因为F是闭集，所以a∈F.引理3证毕.

引理4 设φ为线性压缩映射，若φ的压缩比为ρ，不动点为a,则

φ(x)=ρx+a(1-ρ)，并且φn(x)=a+ρn(x-a),对n≥1.

证明 设φ(x)=ρx+b，则φ(a)=ρa+b，又因为a是不动点，由a=φ(a)，a=ρa+b，得b=a(1-ρ)，故

φ(x)=ρx+a(1-ρ).

(5)

下面用归纳法证明第二个结论.

当n=1时，就是(5)式.设φn-1(x)=a+ρn-1(x-a)，则

φn(x)=φ(φn-1(x))=φ(a+ρn-1(x-a))=ρ(a+ρn-1(x-a))+a(1-ρ)=a+ρn(x-a).

引理4证毕.

设x∈R，令[x]是小于x的最大整数，则{x}=x-[x]为x的小数部分，显然{x}∈[0，1).

下面引理5是一维的kronecker定理.

引理5[5]设a∈Qc，a>0，则{na}n≥1在[0,1]中稠密.

引理6 设a∈Qc，，a>0，则{na-m;m,n∈N}在R中稠密.

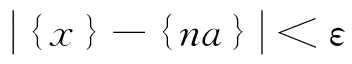
令m=[na]-[m]，引理6得证.

下面定理研究Cλ的自相似子集的压缩比，也是本文的主要结论.

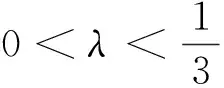
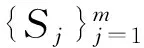
φn(b)=a+ρn(b-a)∈Cλ,对任意n≥1.

(6)

由于有1-Cλ=Cλ我们有

1-φn(b)=1-a-ρn(b-a)∈Cλ,∀n≥1.

(7)

由式(6)和(7)可知，存在c∈Cλ,d>0,使得c+ρ2nd∈Cλ.

下面使用反证法证明.

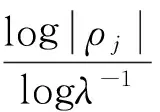
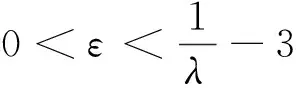
从而ρ2nλ-md∈(1,1+ε),即有

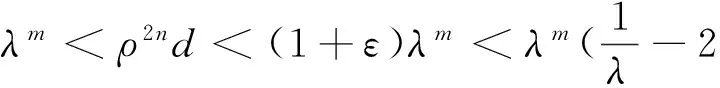
(8)

我们称Si1i2…im([0,1])为m级基本区间，其中i1i2…im是{1,2}上长度为m的词.显然m级基本区间的长度为λm，而相邻m级区间之间的最小间隔为λm-1(1-2λ).

设I是包含点c的m级基本区间，J是包含点c+ρ2nd的m级基本区间.由(8)式左边的不等式，I和J是两个不同的m级基本区间，从而有

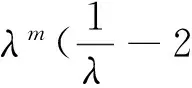
上式与(8)式右边不等式矛盾.

定理1证毕.

[1] Hutchinson J E.Fractals and self-similarity [J].Indiana Univ Math，1981,30：713-747.

[2] Feng D J,Rao H ,Wang Y.Self-similar subsets of the Cantor set[J].Advances in Mathe-matics， 2015，281：857-885.

[3] Hardy G H，Wright E M著.数论导引[M].5版.北京：人民邮电出版社，2008：397-398.

[4] 文志英.分形几何的数学基础[M].上海：上海科学技术教育出版社,1999.

[5] Kenneth Falconer.分形几何[M].北京：人民邮电出版社,2007：113-118.

[6] James R Munkres.拓扑学[M].北京：机械工业出版社,2006：204-205.

责任编辑：周 伦

Discussions about Compression Coefficient of Self Similar Subset of Cantor Set

ZENG Ying

(SchoolofScience,HubeiUniversityofTechnology,Wuhan430068,China)

Many fractals are composed of parts which are similar to the whole in some way,and symmetric Cantor set, which is with similarity, is a typical and vital fractal geometry.We will make further discussion about some properties of compression coefficient of self similar subset of Symmetric Cantor set.

the IFS attractor; symmetric Cantor set; coefficients.

2015-08-27

国家自然科学基金(51109086)

曾 莹(1980—)，女，湖北武汉人，讲师，博士，研究方向：分形几何和动力系统.

1671-9824(2016)02-0006-03

O174.12

A