研题要勤于“走自己的路”——以一类中考题为例

☉江苏省南京市金陵中学河西分校　李玉荣



研题要
勤于“走自己的路”——以一类中考题为例

☉江苏省南京市金陵中学河西分校李玉荣

我们知道，数学课堂教学的素材主要有“教材知识”和“各类题目”两部分构成，而题目又直接体现了数学知识的运用和应用，可以这样说，学生在数学学习上的成长主要是通过解题水平来体现的.因此，要提升学生的数学能力，数学教师必须具有研题的能力.所谓研题，一般指教师在题目教学前、题目教学中、题目教学后对题目自身及解法做的研究工作，它既是数学教师日常教学的一项基本工作，更是永无止境的一门必修课，优秀的数学教师，无一例外都是研题的行家里手.本文围绕一类中考题谈谈教学前研题的思考与认识.

近几年的中考几何命题出现一种现象：有难度的几何题都会设置一些铺垫，虽然命题者的用意是体现对考生的人文关怀，设计合理的铺垫也的确对学生解题有所帮助，但设置的铺垫通常仅仅是命题者预设的解题思路，无疑局限了考生的思维，使其他解法（或许更好）无法施展.作为教师，在接触此类问题时，不能按部就班、就提论题，需要潜心研题，走自己的路——题目铺垫合适吗？还有更好的解法吗？努力使题目的功效最大化.

例1（某市中考模拟题）已知，在△ABC中，∠ABC=45°，D是BC上一点，∠ADC=60°，且CD=2BD，将△ADC沿AD翻折，使点C落在点C′处，

（1）求证：BC′⊥BC；

（2）求∠C的度数.

标准答案：（1）如图1，取DC′的中点M，连接BM.

图1

图2

由翻折知∠ADC′=∠ADC=60°，C′D=CD，所以∠BDC′=60°.因为CD=2BD，所以C′D=2BD，所以MD=BD，所以△BMD为等边三角形.

所以∠MBD=∠MDB=60°，BM=MD=MC′.

所以∠C′BM=∠C′=30°.

从而∠C′BD=90°，故BC′⊥BC.

（2）如图2，作AE⊥BC，AG⊥C′D，AF⊥BC′，垂足分别为E、G、F.

由（1）知∠ABC′=∠ABC=45°，所以AF=AE.

又∠ADC′=∠ADC=60°，所以AG=AE，故AF=AG.

从上面的解题过程看，命题者设置了铺垫的第（1）小题，然后利用第（1）小题得到的一些结论来解决第（2）小题，但是我们看到铺垫的第（1）小题自身也并不容易，且与第（2）小题的联系并不十分明显.因此，教师需要研题：直接求解第（2）小题需要先作翻折变换吗？怎样更合理地利用题中的两个特殊角“∠ABC=45°，∠ADC=60°”？实际上，容易想到的自然解法是作垂线构造直角三角形.

图3

另解：如图3，作CH⊥AD于点H，连接BH，则∠HCD=30°，所以CD=2DH=2BD，所以BD=DH，从而∠HBD=∠BHD=30°.

又∠ABC=45°，所以∠ABH=15°.

又∠BAD=∠ADC-∠ABC=15°，所以AH=BH.

又∠HCD=30°=∠HBD，所以CH=BH=AH，所以∠ACH=45°.

从而∠ACB=∠ACH+∠HCD=75°.

评注：此解法通过添加恰当的辅助线，将问题转化为求∠ACH即可，解法简洁，学生更易于接受.对难题设置铺垫体现了对考生的人文关怀，但铺垫必须精心设置，对学生解题才能真正有所帮助，题目自身的价值才不会丧失.一般而言，当一个题目偏难且解法唯一时，设置铺垫才有必要，否则还是应把思考留给学生，让学生在思考中展示自己的数学潜能，体现“不同的人在数学上得到不同的发展”这一理念.

例2（2015年南京市中考题）如图4，AB∥CD，点E、F分别在AB、CD上，连接EF，∠AEF、∠CFE的平分线交于点G，∠BEF、∠DFE的平分线交于点H.

（1）求证：四边形EGFH是矩形.

（2）小明在完成（1）的证明后继续进行了探索.过点G作MN∥EF，分别交AB、CD于点M、N，过点H作PQ∥EF，分别交AB、CD于点P、Q，得到四边形MNQP.此时，他猜想四边形MNQP是菱形，请在如图5所示的框图中补全他的证明思路.

图4

图5

因为AB∥CD，所以∠BEF+∠DFE=180°，

因为∠FEH+∠EFH+∠EHF=180°，

所以∠EHF=180°-（∠FEH+∠EFH）=180°-90°=90°.

同理可得∠EGF=90°.

因为EH平分∠BEF，所以∠FEH=∠BEF.

因为点A、E、B在同一条直线上，所以∠AEB=180°，即∠AEF+∠BEF=180°.

所以四边形EGFH是矩形.

（2）（答案不唯一）由AB∥CD，MN∥EF，PQ∥EF，易证四边形MNQP是平行四边形.

要证MNQP是菱形，只要证MN=NQ.由已知条件FG平分∠CFE，MN∥EF，故只要证GM=FQ，即证△MGE≌△QFH，易证GE=FH、∠GME=∠FGH.

故只要证∠MGE=∠QFH，易证∠MGE=∠GEF，∠QFH=∠EFH，∠GEF=∠EFH，即可得证.

毋容置疑，这是一道设置新颖、独特的中考题，命题者将一道“证明四边形MNQP是菱形”的题目设置成两个问题，先证明四边形EGFH是矩形，再给出一个留有“空白”的证明思路，让考生补全，体现了过程性原则，意在考查学生做几何题的分析能力.作为教师，教学中对这道题仅仅如法炮制是不够的，需要做的研究是：能用其他更简洁的方法直接证明四边形MNQP是菱形吗？

另证：易证四边形MNQP、MNFE、PEFQ都是平行四边形，所以MN=PQ，ME=NF，PE=QF.

因为EG平分∠AEF，所以∠GEF=∠MEG.

因为MN∥EF，所以∠GEF=∠MGE，所以∠MEG= ∠MEG，所以ME=MG.

所以平行四边形MNQP是菱形.

评注：此证法无需先证明矩形，也无需证明全等三角形，只需利用“平行线+角平分线产生等腰三角形”这一基本图形，问题轻松获解，带给学生的是一次思维的“震撼”，如果再适当安排一些类似习题给学生练习，效果更加明显.

例3（2015年江西省中考题）我们把两条中线互相垂直的三角形称为“中垂三角形”.例如，图6，图7，图8中，AF、BE是△ABC的中线，AF⊥BE，垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a，AC=b，AB=c.

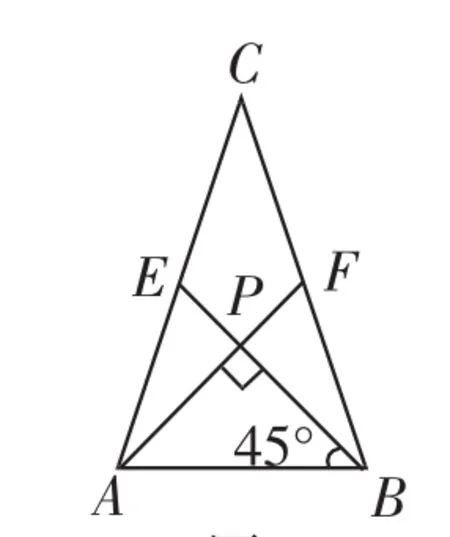
图6

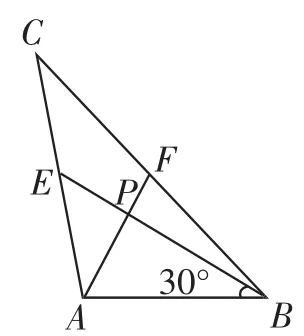
图7

图8

特例探索：

如图7，当∠ABE =30°，c =4时，a =_______，b = _______.

归纳证明：

（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图8证明你发现的关系式.

拓展应用：

（3）如图9，在▱ABCD中，E、F、G分别是AD、BC、CD的中点，AB=3.求AF的长.

图9

（2）a2+b2=5c2（过程略）.

（3）方法一：如图10，设AF、BE交于点P，取AB的中点H，连接FH、AC.

因为E、G分别是AD、CD的中点，F是BC的中点，所以EG∥AC∥FH.

又BE⊥EG，所以FH⊥BE.

因为四边形ABCD是平行四边形，

所以AD∥BC，AD=BC.

所以AE=BF，AE∥BF，所以AP=FP.

所以△ABF是中垂三角形.

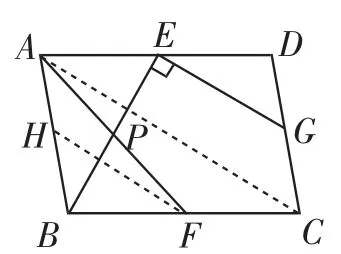
图10

方法二：如图11，设AF、BE交于点P，连接AC、CE，延长CE、BA交于点H.

因为E、G分别是AD、CD的中点，所以EG∥AC.

又BE⊥EG，所以AC⊥BE.

显然△AEH≌△DEC，所以HE=CE，HA=CD=BA，所以BE、CA是△HBC的中线，所以△HBC是中垂三角形.

所以BH2+HC2=5BC2，即所以HC=8.

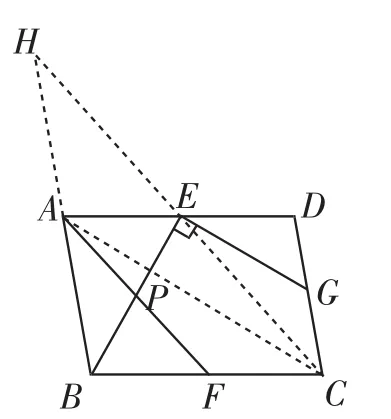
图11

这是一道中考压轴题，题目先定义了“中垂三角形”，然后从特例探索到归纳证明，为学生解题设置铺垫，最终应用发现的结论解决第（3）小题，题目的命制特色鲜明，梯度合理，具有一定的区分度，践行了《数学课程标准》提出的“不同的人在数学上得到不同的发展”的理念.但从第（3）小题的解答过程看，怎样构造“中垂三角形”并不容易.如果将此题作为例题教学，除了按部就班地讲评方法，能否进一步引导学生不走命题者提供的思路，直接求解第（3）小题呢？笔者在课前做了研究：要求AF的长度，一般会想到作垂线构造直角三角形利用勾股定理求解，注意到BE⊥EG，联想到一个与相似三角形有关的基本图形——“一线三直角模型”，可分别过点B、G作AD的垂线，得到如下解法：

方法三：如图12，分别作AH⊥BC，BM⊥AD，GN⊥AD，H、M、N为垂足，则AH=BM，HB=AM.

易证△BMA∽△GND，△BME∽△ENG.

图12

评注：模型思想是《数学课程标准》提出的10个核心概念之一.在本题中，根据图形特点，构造直角三角形、构造相似三角形求解朴素、自然，是几何图形中计算线段的“通法”或“模式”.章建跃博士曾在《中小学数学》中撰文《注重通性通法才是好数学教学》.罗增儒教授在《数学解题学引论》中也指出：“典型模式就像建筑上的预制构件，也是思维的基本模块，本质上是一种标准化设计，即将陌生的问题转化为标准的问题，然后用标准的程序去解决它.在中学数学教学中，‘基本问题’的思想是这一策略的重要表现，积累基本问题也就成为提高这一策略效率的捷径，比如，在几何上有解题的‘基本图形法’，即将一些典型的图形彻底剖析，遇到一个新的图形时，或者将其补充成一个基本图形，或者将其分拆为几个基本图形，然后在基本图形的框架内加以解决.”

教学前的研题，有助于课堂教学中选用例题、习题，使知识的运用更具有针对性，有助于教学中有的放矢地启发、引导和点拨，使教学更有效.教师对现成的题目及标准答案应持尊重但不迷信的态度，善于研究，勤于走自己的路，努力挖掘题目的内涵、揭示问题的本质，通过研题让学生受益、促自己提升，实现教学双赢.