对一道“新定义”型探究题的解法探析与拓展
2016-04-13浙江省绍兴市柯桥区西藏民族中学严浩良浙江省绍兴市柯桥区平水镇中沈岳夫
☉浙江省绍兴市柯桥区西藏民族中学 严浩良☉浙江省绍兴市柯桥区平水镇中 沈岳夫
对一道“新定义”型探究题的解法探析与拓展
☉浙江省绍兴市柯桥区西藏民族中学严浩良
☉浙江省绍兴市柯桥区平水镇中沈岳夫
《新课标》中明确指出,数学在应用方面需要大力加强,鼓励学生发现数学的规律和问题解决的途径,使他们经历知识的形成过程.“新定义”型试题是考查学生数学能力的最好题型之一,它既能考查学生适应新问题、接受新知识、认识新事物的能力,又能考查学生的自学能力,以及信息的收集、迁移和应用能力.此类题型新颖别致,颇具魅力,已成为中考试题中的一朵奇葩,其中对新概念信息的提取和化归转化是求解的关键,也是一个难点.笔者在研究2015年各地的数学中考试卷时,发现江西省中考卷的第24题(压轴题)是一道“新定义”型的探究题,引人入胜,探究味浓,尤其是第(3)小题,可从不同角度思考,巧添辅助线,解法多姿多彩.
一、试题呈现
题目我们把两条中线互相垂直的三角形称为“中垂三角形”.例如,图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索:
如图2,当∠ABE=30°,c=4时,a=_________,b= _________.
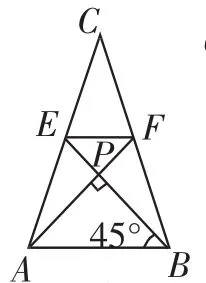
图1

图2

图3

图4
归纳证明:
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式.
拓展应用:
(3)如图4,在▱ABCD中,E、F、G分别是AD、BC、CD的中点,BE⊥EG,,AB=3.求AF的长.
二、解法展示
(2)猜想a2、b2、c2三者之间的关系是:a2+b2=5c2.

图5

(3)由于E、F、G分别是AD、BC、CD的中点,因此对“中垂三角形”的观察角度不同,可以有不同的添线方式,构造多种“中垂三角形”.现列举如下:
思路1:通过添加辅助线,构造出△AFE是“中垂三角形”
如图6,连接AC,EF交于点H,AC与 BE交于点Q.设BE与AF的交点为P,因为E、G分别是AD、CD的中点,所以EF∥AC.又因为BE⊥EG,所以BE⊥AC.因为四边形ABCD是平行四边形,所以AD∥ BC,∠EAH=∠FCH.

图6

图7
思路2:通过添加辅助线,构造出△EDC是“中垂三角形”
如图7,连接EC,DF,由上述的解题思路,易证△DEC是“中垂三角形”,所以由(2)的结论可得CD2+CE2=5DE2,即所以CE=4,所以AF= 4.
评注:思路1、思路2所添的辅助线都是把目光盯在平行四边形ABCD的内部,构造出“中垂三角形”.思路1侧重于借用中位线和三角形全等求解,连接AC起到构造△AFE是“中垂三角形”的桥梁作用.思路2是注意到AE∥FC,连接EC,构造出△DEC是“中垂三角形”,然后获解.当然此题还可以有其他解法,如连接AC及过点F作AC的平行线交AB于H点,构造“中垂三角形”△ABF,这一思路留给有兴趣的读者去思考.
思路3:通过添加辅助线,构造出△BCH是“中垂三角形”

图8
如图8,连接AC,CE,延长CE交BA的延长线于点H.在△ACD中,因为E、G分别是AD、CD的中点,所以EG∥AC.又因为BE⊥EG,所以BE⊥AC.又因为四边形ABCD是平行四边形,所以AE∥,BC =2AE,所以△HAE∽△HBC,所以所以HA= AB,AE=EC,所以BE、CA是△HBC的中线,所以△BCH是“中垂三角形”,所以由(2)的结论可得HB2+HC2=5BC2,即所以HC=8.因为AF是△BCH的中位线,所以
评注:思路3所添的辅助线是把目光盯在平行四边形ABCD的外部,构造出“中垂三角形”.思路3是受图1、图2的启发,且AE∥BC,构造出字母“A”型的相似三角形,再连接AC,可证△AFE是“中垂三角形”.同样,此题还可以有其他解法,有兴趣的读者可去尝试思考.可见,通过合理的构造、添辅助线可以在条件和结论之间架起一座“桥”,把一个复杂问题的条件明朗化,使问题获得简捷明了的解答方法.
三、拓展探究
事实上,该题第(3)问,除去“伪装”,即摘除面纱之后,我们可发现,其实就是三角形中线定理(pappus定理,又称阿波罗尼奥斯定理),露出了“真容”.
中线定理:三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍.

图9
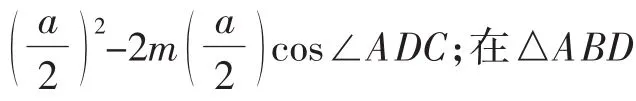
那么第(3)问,如果知道AC的长,则代入相关线段的值,可直接求出AF的长.那么如何求AC的长呢?


图10
到此,通过对该题的解法探究,揭示了命题中条件与隐含条件、结论的内在联系,为寻求解题途径指明了方向,使得问题的解决更具有一般性,可谓别具一格.本结论(指中线定理)可作为中考题和中学竞赛题方面的试题原型设置题目,灵活运用,不但可以培养学生的发散思维,而且还能开拓学生的视野,提高解题能力,对提高学生学习数学的兴趣大有帮助.
参考文献:
1.沈岳夫.一类“新定义”型的抛物线试题赏析[J].中学数学(下),2015(9).
2.高东.对一道经典压轴题的探析与建议[J].中学数学(下),2015(1).
3.邓文忠.中考新定义抛物线问题探析[J].中学数学杂志(初中版),2015(2).
