HPM视角下“三等分角”习题课教学与思考

2016-04-13江苏省苏州市阳山实验初级中学仲进东

中学数学杂志 2016年4期

☉江苏省苏州市阳山实验初级中学　仲进东

☉江苏省苏州市阳山实验初级中学仲进东

一、数学史话

将数学史与数学融合在一起共同促进学生的发展是HPM（Historyand Pedagogyof Mathematics）研究的一个主要涵义.我们知道，三等分角是古希腊三大几何问题之一.即在尺规作图（即用没有刻度的直尺和圆规作图）的前提下，无法将一个给定的角三等分.若将条件放宽，却可以引发三等分的作法.比如历史上关于“三等分角”的故事的版本很多，其中有一段是与阿基米德有关.这里简要概述这段故事.

公元前4世纪，亚历山大城的工匠们试图用尺规作图法确定出桥的位置，可是他们用了很长的时间也没有解决.问题的本质是用尺规作图解决三等分角，于是他们去请教阿基米德.阿基米德用在直尺上做固定标记的方法，解决了三等分一角的问题.正当大家称赞阿基米德了不起时，阿基米德却说：“这个确定北门位置的方法固然可行，但只是权宜之计，它是有破绽的.”阿基米德所谓的破绽就是在尺上做了标记，等于是做了刻度，这在尺规作图法中是不允许的.

受到这个故事的启发，我们针对八年级学生（已学习初中几何全等三角形、角平分线的性质与判定、垂直平分线的性质与判定），设计了一节习题课，取得较好的教学效果.本文先展示该课的教学设计，并进一步阐释相关思考，供研讨.

二、“三等分角”习题课教学设计

活动一：作已知角的平分线

问题1：尺规作图作出已知角的角平分线.

问题2：尺规作图作出一个60°角.

问题3：尺规作图作一个平角的三等分线.

设计意图：开课阶段安排学生复习一些基本作图及作法，为本课的探究作必要的准备.由于这些基本操作都是应知必会的技能，这里不展示相关素材.

活动二：学习使用阿基米德的“角尺”工具

通过PPT图文介绍上文中提及的阿基米德设计的“角尺”（如图1）.

图1

解说：该“角尺”是由两个等宽的直尺拼接而成，其中一个直尺上标有等距离的刻度.

下面以三等分∠ABC为例说明利用“角尺”三等分锐角的过程.

第一步：画直线DE使DE∥BC，且这两条平行线的距离等于PQ（即角尺上直尺的宽）；

第二步：移动并调整“角尺”到如下位置，使其顶点P落在DE上，使“角尺”的MN边经过点B，同时让点R落在∠ABC的BA边上；

图2

第三步：标记此时点Q和点P所在的位置，作射线BQ和射线BP.

问题4：射线BQ和射线BP是∠ABC的三等分线吗？

预设：连接BP，作PH⊥BC于H点，根据作法及垂直平分线的性质容易证明∠RBQ=∠QBP=∠PBC.从而确认射线BQ和射线BP是∠ABC的三等分线.

活动三：制作简易“角尺”三等分60°角

活动准备：每人准备两张A4纸，双面胶.

制作“角尺”：将两张A4纸对折成两个长条状长方形纸条，其中一个长方形纸条连续折出正方形折痕（折痕即刻度），用双面胶将两个长方形纸条如图1一样贴好.

使用“角尺”：利用“角尺”将活动一中的尺规作图对60°角进行三等分.

活动组织：同桌可以分成一组，制作“角尺”后交流他们的制作与使用心得.并安排2～3个小组派出代表走上讲台运用实物展台展示“角尺”和三等分角的操作过程.

活动四：提出问题，拓展思考

问题5：小贾同学在图2的基础上，作射线BS，他纠结于∠SBR是不是∠ABC的三分之一，可是又不会证明，你能帮助小贾同学辨别一下吗？

预设：只要说明∠SBR不等于∠RBQ即可，可以把目光聚焦在直角△SBQ中，BR是中线，它就不可能是角平分线了！否则，就可证出BS=BQ了！

问题6：在图2中，能否在∠ABC外部，作射线BV，使∠ABV=∠ABC呢？

图3

图4

预设：如图4，作QH⊥AB于H，再截取HG=HQ，作射线BG，则射线BG就是所求的射线BV.

问题7：尺规作图将一个平角四等分.

预设：只要使用尺规连续作两次角平分线即可.

问题8：使用“角尺”将一个直角四等分.

预设：先调整“角尺”的位置（如图5），得到直角的角平分线（作射线BP），再调整“角尺”的位置（如图6），注意需要利用“角尺”的度量功能保证BR=BD，这时作出射线BM可得到45°角的角平分线.

图5

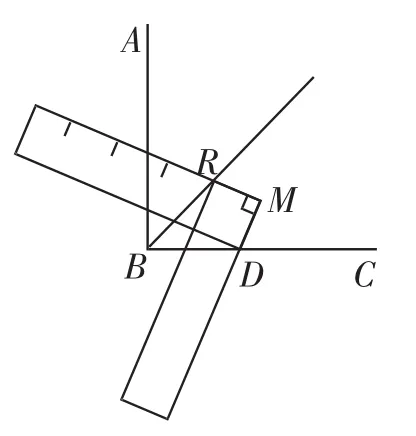
图6

三、关于HPM融入日常教学的三点思考

上面结合“角尺”给出一个三等分角的习题课教学设计，概述了教学流程和各环节的操作建议，以下再由该课例出发，就HPM融入日常教学提出三点思考.

1.基于HPM构思教学设计是深刻“理解数学”的体现

由于引入数学史话进入课例设计必然涉及教师要广泛阅读、涉猎相关数学史的著作或文献，弄清教学内容在数学历史上的先后顺序，包括这些教学内容是如何被数学家们发现、证明的，其中的经历是如何的曲折，背后的故事版本往往也多样，如何鉴别取舍，甚至在引入课堂教学中来时还需要教者本人进行改编.事实上，这样的过程正是教者本人深入理解数学的过程，也是践行章建跃教授提出的“理解数学”的体现.正是在这样的角度上，我们预设阿基米德“角尺”的数学情境贯穿于整节课中，除了实现解题教学的功能，还给学生留下一个大大的“？”，即尺规作图为什么不能进行三等分角？如何证明这个命题呢？限于初中学段知识所囿，只能让学生存疑，待日后有兴趣的学生进入更高层次的数学学习时再去攻克和理解.

2.基于HPM的教学设计要从“嵌入”走向“融入”或“重构”

我们发现，不少基于HPM视角开发的课例多是数学史话的“附加式”或“嵌入式”，与学者们提出的“数学史引入中学数学教学的方式，应以‘融入’的方式为主”相去甚远.这方面的课例突出的是勾股定理的新授课，很多老师执教时喜欢引入一段所谓的数学史话，包括教材上也把毕达哥拉斯发现和证明勾股定理的灵感用到在朋友家坐客时受到地面砖的启发.然而有些类似的数学史话如果从该课中删除的话，完全不影响整节课的效果，甚至还能起到削枝强干的作用，那么这样的数学史话作为一种点缀，不要也罢.这样来看，以华东师大汪晓勤教授领衔的促进数学史融入课堂教学就是值得践行的一种有效方式.在上文课例中，我们试图通过阿基米德的一段关于“角尺”的传说重构一个古老的数学情境，将尺规作图与工具作图互动起来，既指向理性文化，又沟通数学的实用主义，应该是一次有积极意义的数学史融入课堂、重构教学内容的尝试.

3.基于HPM设计系列追问，促进教学对话

章建跃教授提出的“三个理解”中还有“理解学生”和“理解教学”，在这两者的角度来看，基于HPM设计教学内容时，要注意围绕一个主干问题设计系列追问，贴近学生熟悉的情境，根据教师对教学环节的熟悉，设计逻辑连续的问题是课堂教学的关键.在上文的课例中，全课，我们在不同教学环节中，一共预设了8个系列问题，注重关联，加强互动，使得各个教学活动之间过渡平滑.这样的努力，才努力追求开放式教学、对话式教学，在对话中倾听学生的表达，欣赏学生的展示，并适时作出恰当的评价和追问，有效追求了精心预设与动态生成的课堂教学.