顾及控制点均匀性的无人机实景三维建模精度分析

成李博，李佳，段平，王云川

(云南师范大学地理学部，昆明 650500)

0 引言

实景三维模型能够模拟真实地物的地理要素，被广泛应用于古建筑重建[1-2]、自然灾害检测[3-4]、国土规划[5]、城市建设[6]等方面.无人机（UAV）航空影像作为一种构建实景三维模型的重要数据源，因其获取数据效率高、成本低、精度高等优点成为当下主流的数据获取方式.

由于UAV搭载的小像幅相机，获取的航空影像像幅较小，要求影像之间应保持较高的重叠区域.这就导致采用传统的摄影测量布点方式对控制点的需求量较大[7].研究如何使用较少的地面控制点来满足计算需求成为需要解决的问题.由于控制点会随飞行航向与旁向布设密度不同而有差异[8]；同样也会因绘图比例尺不同，使得所需控制点数目也不相同[9]；不同区域，如冰川、水域、非规则地区对控制点布设的要求也不相同[10-12]；不同类型传感器所需控制点布设也不相同[13].使得寻找一种普适性解决方案变得较为困难.许多研究也试图从控制点分布的数量上和空间密度上寻找解决方案[8,14].

尽管控制点布设的数量和密度差异会影响实景三维模型的生产精度[15-16].但是控制点数量和密度仅顾及了研究区的局部范围，相同控制点数量或密度下，控制点在整个研究区上具有不同的均匀性.如何从顾及控制点均匀性角度出发[17-19]，探究其对UAV实景三维模型精度的影响，成为本研究要探讨的内容.

1 控制点均匀性算法

均匀性是对空间点集复杂性的一种测度，描述了点集的空间关系，可通过某种度量方法来确定.控制点作为一种点集分布在地表，其具有空间复杂性的特性，换言之，控制点在空间分布的均匀性可通过定量化方法来确定[18].

为了确定实验区控制点分布的均匀性，首先，做以下假设条件：令Y={Y1,Y2,···,Yn}是地表上的控制点集，ρ={ρ1,ρ2,···,ρn}是控制点集的均匀性.要计算控制点集的均匀性ρ，需求解两个参数：点集Y中最小距离点对的一半、点集Y的最大空圆的半径，分别记为qY、hY.均匀性ρ的表达式如下：

式中，

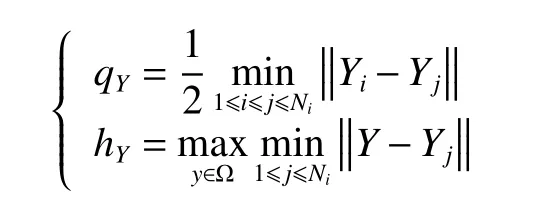
式中：N为当前地表控制点的总数；Ω为Y的凸壳.

求解最大空圆的半径.最大空圆是指不包含控制点集Y中任何控制点的最大圆，且该圆的圆心位于以点集Y为凸壳的内部，凸壳示意图如图1(a)所示.要求解最大空圆，需确定所有可能的圆心，计算步骤为：1）计算点集Y的凸壳、点集Y的Voronoi图，图1(b)为Voronoi示意图；2）计算凸壳和Voronoi图的交点；3）以Voronoi图的顶点和步骤2）中求解的交点作为可能的圆心.以圆心画出最大圆，且圆内不包含任何控制点，即最大空圆，如图1(c)所示.此时，最大空圆对应的半径为所求最大空圆的半径.

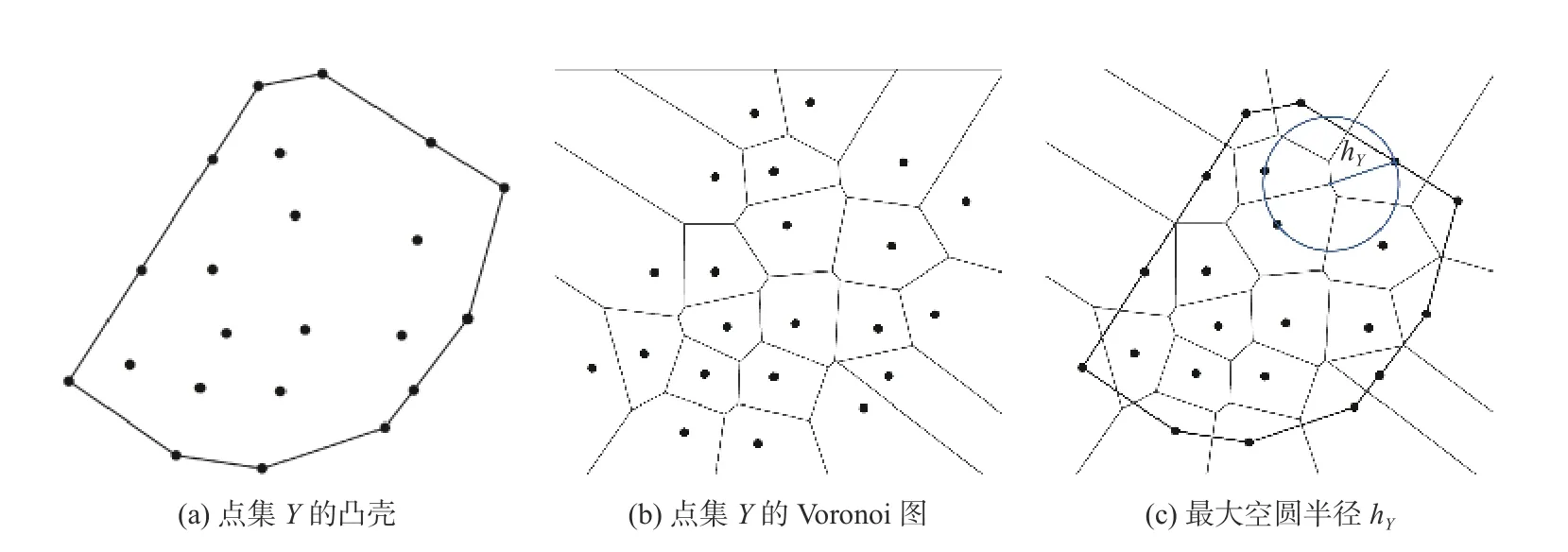
图1 求解最大空圆半径

根据点集Y中最小距离点对的一半qY和最大空圆的半径hY计算控制点的均匀性ρ.以此为布设控制点的依据，探究不同均匀性下控制点对构建无人机实景三维模型的精度影响.

2 实验区与实验数据简介

2.1 实验区概况

以云南省呈贡区万溪冲村南部某开发区空地为研究对象.如图2所示，该区域面积约0.52 km2，平均海拔2003m，地形分布呈西南-东北朝向.区域周围无电磁波和高大建筑物对飞行信号干扰.

2.2 无人机数据获取

数据采集设备使用大疆精灵4Pro无人机.采集时间为2019年1月26日，当日天气晴朗，光线充足且曝光适中，是无人机影像采集的最佳时间.飞行时航向设计为东南-西北向，使用航线规划软件布设飞行航线：航向重叠度80%，旁向重叠度75%.飞行时接收卫星颗数10颗，飞行高度约85m.本次飞行共采集607张航空影像.使用徕卡实时动态（RTK）测量仪获取36个地面控制点，将控制点坐标统一到投影坐标系下.

图2 实验区

2.3 实验布设及均匀性计算

布设控制点.36个控制点中，26个点用于平差建模计算，10个点作为检查点用于模型精度验证.图3为实际作业过程，以靶标中心作为控制点的量测部位.本研究设计了两种不同数目控制点实验(不同量纲)，每种实验中各包含3组控制点布设方案.在实际作业时，为了减少建模中的人为误差，所有方案中公共控制点使用同一次量测结果.同理，所有方案中使用同一组检查点.研究区的4个角点分别布设有一个控制点，确保后续实验是在整个试验区被控制点控制的基础上进行的.检查点与角点分布如图4(a)所示.

计算控制点的均匀性.首先，根据控制点均匀性算法求解出每组方案中控制点之间的最小距离点对的一半qY和最大空圆的半径hY；通过式(1)计算得到每组方案下控制点的均匀性ρ.如图4所示，两种控制点实验中分别包含5个和8个控制点，每个实验根据控制点的均匀性分为3组布设方案.如图4(b)、(c)、(d)所示，当控制点数目为5时，3组布设方案的均匀性ρ分别为0.179 7、0.2597、0.4633，且根据ρ的大小将三组实验记为ρ5−l、ρ5−m、ρ5−h，其中l、m、h分别表示低、中、高三种均匀性，下同；如图4(e)、(f)、(g)所示，当控制点数目为8时，均匀性依次为0.100 5、0.263 1、0.422，分别记ρ8−l、ρ8−m、ρ8−h.

图3 控制点采集场景

图4 实验区域检查点、角点、控制点布设方案

2.4 无人机实景三维模型构建

无人机实景三维模型构建的主要步骤有：无人机数据采集与处理、空中三角测量、密集匹配、模型构建、纹理映射等，如图5所示.具体过程为：1）借助无人机设备获取实验区航空影像，进行筛选，剔除不合格影像，对合格影像做校正、去噪、匀色、增强处理；2）通过影像的位置姿态信息做影像匹配、连接点提取，与地面控制点数据参与平差计算，将影像的相对坐标转换到大地绝对坐标系下，计算出影像的外方位元素；3）对空中三角测量获得的稀疏点云稠密化得到稠密点云；4）将稠密点云转换为不规则三角网（TIN）模型，根据TIN之间的内部关系做平滑和优化处理；5）利用TIN模型的空间位置获取与之相对应的纹理特征，赋予模型纹理语义.

图5 实景三维建模流程

2.5 数据精度评价

经处理后的影像覆盖整个实验区域，加入控制点量测数据进行建模构建.控制点误差是指模型测量值与RTK值的差的绝对值.在控制点参与建模的前提下构建航高85m下的实景三维模型，并统计了参与均匀性计算的22个控制点的误差的标准Q-Q图，如图6所示.控制点误差分布符合正态分布，满足分布规律，可用于后续探讨.

图6 控制点误差标准Q-Q图（X、Y、Z 方向）

3 无人机实景三维模型构建与检查点精度分析

3.1 无控制点分布情况下检查点误差分析

三维模型的精度是通过检查点来衡量的，通常是指检查点的模型坐标与实际坐标的中误差.中误差包括平面和整体中误差：平面中误差描述检查点在X、Y轴上的整体误差；整体中误差是指X、Y、Z三个坐标轴上检查点的整体误差.平面中误差Mpla和整体中误差Mall的求解公式如式（2）所示：

式中：αx、αy、αz为检查点在X、Y、Z轴三个方向上的中误差；n代表检查点数目，这里n为10；∆2为检查点误差的二范数；Mpla为平面中误差，Mall为整体中误差.

由表1可知，无控制点参与建模计算时，模型平面和整体上的误差较大.平面误差的大小取决于航测时全球卫星导航系统（GNSS）的数据精度.一般的，GNSS信号受高大建筑物和电磁波信号影响，实验区及周围不存在这两种信号干扰因素，出现的误差较大是由于无控制点参与平差计算引起的.由此生成的实景三维模型精度较差，不具有研究和使用价值，后续不被用于讨论.

表1 不同数量下不同均匀性的控制点分布于试验区时检查点的误差 m

3.2 顾及控制点均匀性的误差分析

验证不同均匀性下控制点对模型精度的影响.当控制点数为5时，计算控制点均匀性分别为ρ5−l、ρ5−m、ρ5−h时检查点的误差，如表1所示.10个检查点在X、Y、Z三个坐标轴上的绝对误差分布情况如图7所示.当控制点均匀性为ρ5−l时，检查点在X、Y轴方向上误差处于0.1m左右，Z轴误差较大；当控制点均匀性增加到ρ5−m时，检查点的误差在X和Y轴方向上减小到0.022m左右，Z轴上误差减小到0.06 m附近，整体误差从0.954 4 m下降到0.0656m.从图7中可以看到，控制点均匀性从ρ5−l增加到ρ5−m后，检查点在平面上的绝对误差趋于集中，且中位数降低，Z轴方向上绝对值误差仍然呈现分散状态；继续增加均匀性到ρ5−h时，检查点在三个坐标轴方向上的误差均趋于最小，整体中误差为0.0556m，且绝对误差整体呈现集中分布的现象.

图7 采用5个控制点且控制点均匀性为ρ5−l、ρ5−m、ρ5−h 时检查点误差分布

控制点的数量为8时分析不同均匀性下检查点对模型精度的影响.3组控制点均匀性分别为ρ8−l、ρ8−m、ρ8−h，检查点的中误差如表1所示.10个检查点在三个坐标轴方向上的绝对误差分布如图8所示，三种方案下所有检查点的绝对误差均小于0.2m.由表1可知，当控制点的均匀性最低时，检查点在X和Y轴方向上的误差处于0.0605m左右，Y轴方向误差较大为0.1128m；增加控制点的均匀性到ρ8−m时，三个坐标轴的误差均有所下降，但绝对误差仍呈现分散现象；继续增加控制点的均匀性到ρ8−h时，三个坐标轴的误差趋于最小，均小于0.042m，除Z轴绝对误差稍微分散外，X、Y轴方向上绝对误差均集中分布，且中位数较低.整体上，控制点数为8时，三种方案下所有检查点的误差均较小.

图8 采用8个控制点且控制点均匀性为ρ8−l、ρ8−m、ρ8−h 时检查点误差分布

综上，当控制点均匀性较小时，同等数量控制点条件下，增加控制点均匀性有助于提升三维模型的精度；控制点均匀性的提升对均匀性较低时模型精度的改善较高.

3.3 控制点与检查点位置相对分布下检查点误差分析

为了进一步分析检查点与控制点相对分布条件下控制点对模型的误差分布情况，即检查点位置不变时控制点位置随均匀性变化对模型精度的影响.如图9所示，将控制点与检查点的坐标值做归一化处理，检查点在X、Y轴方向上的误差用绝对误差表示，误差大小对应检查点上误差棒的长短.控制点数量为5时，当均匀性为ρ5−l，有3个检查点在X轴方向上绝对误差较大，3个检查点在Y轴方向上存在较大的绝对误差；增加控制点均匀性到ρ5−m时，两个坐标轴方向上绝对误差均呈现下降趋势，且远离控制点的区域绝对误差较低；再次增加控制点的均匀性，10个检查点中仅剩余两个检查点在X轴方向上有较小的绝对值误差.

控制点数量增加到8时，检查点在X、Y轴方向上整体绝对误差较小.当均匀性为ρ8−l时，存在3个X轴方向和3个Y轴上具有较大的绝对误差，且误差远离控制点，是由于检查点远离控制点误差传播造成的；当控制点均匀性为ρ8−m时，Y轴方向减小了一个绝对误差较大的点，即进一步提高了模型在Y轴方向上的精度，且X轴方向上模型精度也得到了提升，具体体现在大幅消减了一个检查点在X轴的绝对误差，其余检查点在X轴的绝对误差也得到了优化；进一步提升控制点均匀性，模型在X和Y轴方向上的精度均得到了提升，只存在一个X轴方向上较大绝对误差点.

观察Z轴方向上模型误差的分布情况.如图10所示，当控制点数量为5且均匀性较低为ρ5−l时，模型误差较大，越远离控制点误差越大；如图10(c)、(e)所示，增加控制点均匀性，即使检查点远离控制点分布，检查点的垂直绝对误差也较小，换句话说，控制点均匀性较高时模型整体精度较高.增加控制点数为8时，当控制点均匀性为ρ8−l，模型在Y轴的绝对误差较大；如图10(d)、(f)所示，增加控制点均匀性，检查点绝对误差继续降低，在此情况下，模型具有较高的精度.

总体上，增加控制点的均匀性，使得模型具有较高的精度.具体表现在，远离控制点的区域会受控制点均匀的分布带来区域上的控制效益.

图9 两种数量控制点下，不同均匀性控制点对检查点水平方向误差的影响

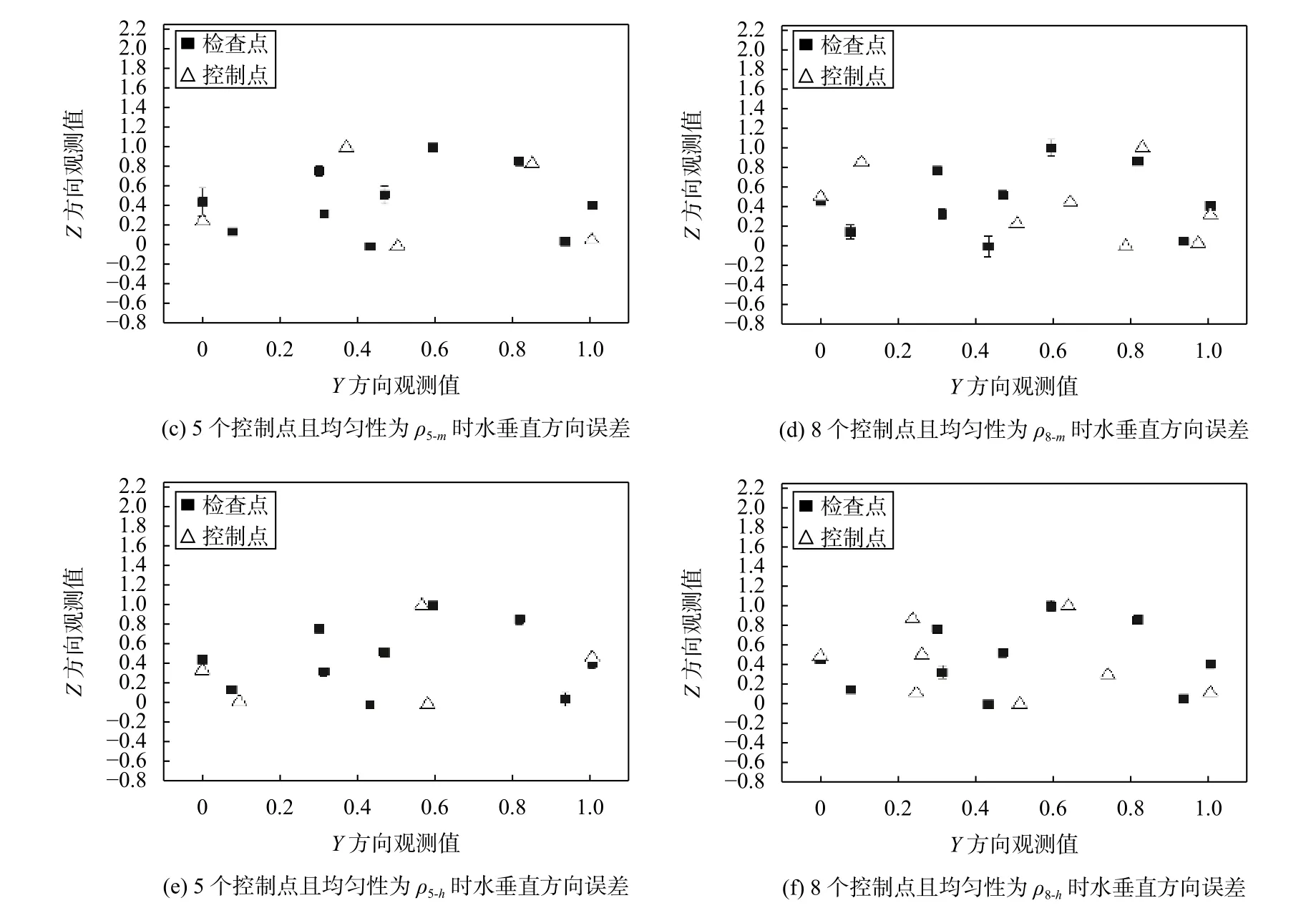
图10 两种数量控制下，不同均匀性控制点对检查点垂直方向误差的影响

4 结束语

UAV在摄影测量中对控制点的布设要求很高，均匀性作为一种衡量控制点布设的方法，科学指导外业测量工作的进展.本研究旨在分析控制点的均匀性对构建实景三维模型精度的影响程度.以云南省昆明市呈贡区建筑空地为研究对象，使用UAV进行低空航摄影像和控制点获取.实验中分为两种数目控制点的布设原则，每种控制点数目下包含3组均匀性布设方案.经分析对比发现：1）控制点均匀性较低时，构建的实景三维模型精度较低，高程方向误差大于平面误差；2）增大控制点均匀性，模型在三个坐标轴方向上误差均降低，且均匀性的提升对处于较低均匀性下模型精度的改善较高；3)控制点均匀性可作为一种评价指标应用到外业控制点量测中去.