Banach空间集合覆盖数估计的新方法

钟延生

(福建师范大学数学与计算机科学学院，福建福州350117)



Banach空间集合覆盖数估计的新方法

钟延生

(福建师范大学数学与计算机科学学院，福建福州350117)

摘要:研究集合的Hausdorff( Fractal)维数时，对覆盖数的估计至关重要．以往Banach空间的集合覆盖数的估计都是通过构造等距同构的抽象方式来实现的．而本文通过构造Banach空间X满足算子范数‖P‖= 1的投影算子P，对集合作投影分解，并结合乘积集合的性质，得到了Banach空间X中子集BF(r2)( 0)，以半径r1(≤r2)的球作覆盖的最小个数的一种新估计，由此为Banach空间X集合的覆盖数给出了一个更为直观的估计方法．其中BF(r2)( 0)B(r2)( 0)∩F，B(r2)( 0)是X中原点为球心、半径为r2的球，F是Banach空间X有限维子空间．

关键词:Banach空间;半径;幂等算子

在有关无穷维动力系统吸引子以及指数吸引子的维数研究中，覆盖定理起着至关重要的作用［1－5］．Mañé通过证明Rn与Banach空间X的n维子空间F存在等距同构，首次给出了集合BFr2( 0)的最小覆盖数的一种估计(文献［6］引理2．1)．此后，通过构造等距同构证明Banach空间集合覆盖数成为共识，Carvalho等也是通过结合实Banach空间的Banach－Mazur距离的最优上界证明等距同构的存在性，给出了一个覆盖定理(文献［2］引理2．3)．

以上都是在证明存在等距同构的基础上完成的，而等距同构概念本身稍显抽象．Temam在Hilbert空间通过直交投影的方法得到了另一个覆盖数估计定理(文献［5］引理3．1)．受此启发，本文由有界线性泛函结合Hahn－Banach定理构造Banach空间满足算子范数‖P‖= 1的投影算子P，借此对集合作投影分解，并结合乘积集合的性质得到集合覆盖数的一种新估计，从而为Banach空间集合的覆盖数给出一种更为直观的估计方法．

记X是Banach空间，P为投影算子，⊕为直和分解．

1构造投影算子

首先，给出直和分解与幂等算子的定义:

定义1［7］若对任意的x∈X，存在唯一的分解式

则称Banach空间X有直和分解X=X1⊕X2．

定义2［7］设映射P: X→X，若P2=P，则称P是一个幂等算子．

关于幂等算子有下面的性质:

引理1［7］设P: X→X是一个有界线性幂等算子，则X=X1⊕X2，其中X1{ x: Px=x}，X2{ x: Px= 0}．

由此，给出投影算子P:

定理1设X1是X的任一一维子空间，则存在投影算子P: X→X1满足‖P‖X→X1= 1，同时有I－P: X→X2满足‖I－P‖≤2且X=X1⊕X2．其中I表示恒等算子，‖·‖表示算子范数．

证明取非零元x0∈X1，则X1{αx0:α∈R}．定义x'为X1上的一个有界线性泛函为

则‖x'‖X*=1及x'( x0) =‖x0‖X．由Hahn－Banach定1理，x'可延拓为X上的有界线性泛函(仍记为x')且‖x'‖X*=1．

再令

接下来证明上述P为投影算子．由引理1可知等价要证P是一个有界线性幂等算子．

事实上，对任意x1，x2∈X有

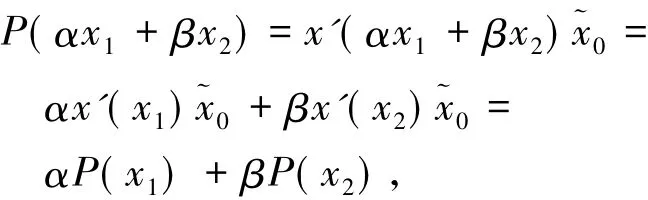
所以P为有界线性算子．又由于对任意y∈X1，存在k，使得y=及

故P是满射．

进一步，对∀x∈X，有

综上可知，P为有界线性幂等算子．

故X=X1⊕X2，其中X2{ x∈X|P( x) = 0}，X1{ x∈X|P( x) = x} ={αx0:α∈R}．

引理2‖P‖X→X1=1．

因为

而由

结合式( 1)和( 2)，有‖P‖X→X1=1，且有即定理1得证．

注1若上述定理1中X1是X的任一n维子空间，则存在投影算子P: X→X1满足‖P‖X→X1≤n．证明参见Auevbach定理(文献［8］定理2．1．16)．

2覆盖定理

下面，结合上节的投影算子给出Banach空间集合覆盖数的一种新的更为直观的估计方法．

定理2设F为X的任意一个m维子空间，则对任意r2≥r1＞0有

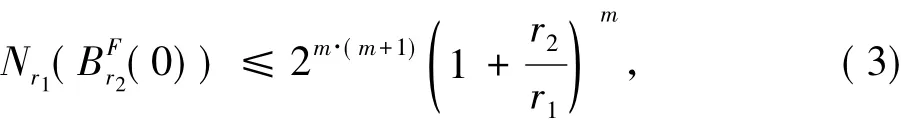
其中BFr2( 0)表示Br2( 0)∩F，Nr1( BFr2( 0) )表示以r1为半径的球覆盖集合BFr2( 0)所需的最小个数．

要证定理2，需如下简单的引理:

引理3设X=X1⊕X2(满足定理1)，B是X中以原点为圆心的球．若集合B∩X1以ε为半径的球的覆盖数是N( X1，ε)，集合B∩X2以ε为半径的球的覆盖数是N( X2，ε)，则N( B，2ε)≤N( X1，ε)·N( X2，ε)，其中N( B，2ε)是以2ε为半径的球覆盖集合B的最小个数．

注2若引理3中X1的维数为n，则结果改为

证明记乘积集为E×F ={ ( x，y) | x∈E，y∈F}．显然，球B可被已知覆盖B∩X1、B∩X2的所有球的乘积集合所覆盖，且个数至多是N( X1，ε)·N( X2，ε)．又由于‖P‖=1及‖I－P‖≤2，从而这些乘积集合的最大半径不超过2ε，因此，

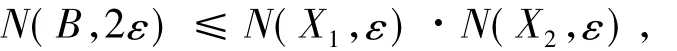
证毕．

现证定理2．

证明采用数学归纳法．

其次，设式( 3)对m－1成立，要证关于m也成立．

取非零点x0∈BFr2( 0)且记X1{αx0:α∈R，x0∈BF( 0) }，结合定理1，可知存在投影算子P满足

r2‖P‖X→X1=1．

因此，关于子空间F，也有相应的直和分解:

121122

F及dimF1= 1，dimF2= m－1．进一步，对任意x∈BFr2( 0)有

1BFr2( 0)最小个数Nr1( BFr2( 0) )满足

故式( 3)对m也成立，证毕．

3结论

上述证明过程中利用泛函分析中重要Hahn－ Banach定理对有界线性泛函作延拓，构造出投影算子，由此对集合作直和分解来得到覆盖数估计，而不需去研究等距同构算子的性质，因此证明方法显得更为直观．而且在证明的过程对乘积集合覆盖数，特别是覆盖半径与投影算子的范数的关系，得到了新的理论结果(即引理3，注2)，从而丰富了覆盖定理的证明方法及其相关内涵．

参考文献:

［1］ROBINSON J C．Dimensions，embeddings，and attractors ［M］．Cambridge: Cambridge University Press，2011: 7－30．

［2］CARVALHO A N，LANGA J A，ROBINSON J C．Finite dimensional global attractors in Banach spaces［J］．Journal of Differential Equations，2010，249( 12) : 3099－3109．

［3］DUNG L，NICOLAENKO B．Exponential attractors in Banach spaces［J］．Journal of Dynamics and Differential Equations，2001，13( 4) : 791－806．

［4］EFENDIEV M，MIRANVILLE A．The dimension of the global attractors for dissipative reaction－diffusion systems［J］．Applied Mathematics Letters，2003，16( 3) : 351－355．

［5］TEMAM R．Infinite－dimensional dynamical systems in mechanics and physics［M］．New York: Springer Verlag，1997: 366－368．

［7］江泽坚，孙善利．泛函分析［M］．北京:高等教育出版社，1992: 190－197．

［8］俞鑫泰．Banach空间几何理论［M］．上海:华东师范大学出版社，1984: 120－121．

A New Estimate of Covering Number for Set in Banach Space

ZHONG Yansheng

( School of Mathematics and Computer Science，Fujian Normal University，Fuzhou 350117，China)

Abstract:The covering number is one important basis for the research on the Hausdorff ( or Fractal) dimension of set．In the past，the estimate of this number in Banach space was performed by constructing the isometry operator．However，a new estimate of the minimal number of the covering balls with radius r1for the subset BF(r2)( 0)⊂X was obtained，by constructing the project operator P with norm‖P‖= 1 in Banach space X，and then making a projecting decomposition on the set with the property of covering number on product set．It supports a more intuitive approach to estimate the covering number of the set in Banach space．Here BF(r2)( 0)B(r2)( 0)∩F; F is a finite dimensional subspace of X; B(r2)( 0) is a ball centered in 0 with the radius r2in X．

Key words:Banach space; radius; idempotent operator

基金项目:国家自然科学基金( 11401100) ;福建省教育厅B类基金( JB14021) ;福建师大校创新团队基金资助项目( IRTL1206)

收稿日期:2014－12－01录用日期: 2015－05－11

doi:10．6043/j．issn．0438－0479．2016．01．018

中图分类号:O 177．91

文献标志码:A

文章编号:0438－0479( 2016) 01－0094－03

Email: zhyansheng08@ 163．com

引文格式:钟延生．Banach空间集合覆盖数估计的新方法［J］．厦门大学学报(自然科学版)，2016，55( 1) : 94－96．

Citation: ZHONG Y S．A new estimate of covering number for set in Banach space［J］．Journal of Xiamen University( Natural Science)，2016，55( 1) : 94－96．( in Chinese)