判定直线平行“四途径”

□吴行民



判定直线平行“四途径”

□吴行民

平行线在现实生活中随处可见，它构成了平面内两条直线的基本位置关系.下面简要介绍判定直线平行的四种途径.

途径一：利用对顶角的性质、等量代换

例1如图1，已知：直线AB、CD相交于点E，∠A=∠1，∠2=∠B，试说明：AC∥BD.

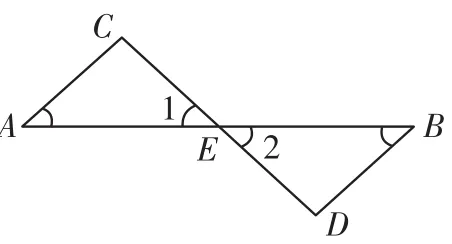
图1

分析：依据判定直线平行的条件，本题需要寻找相等的同位角或内错角，或互补的同旁内角.

解：因为直线AB、CD相交于点E，所以∠1=∠2（对顶角相等）.又因为∠A=∠1，∠2=∠B（已知），所以∠A=∠B（等量代换），所以AC∥BD（内错角相等，两直线平行）.

点评：平行线的判定是以角的相等或互补为前提的.本题的关键是借助对顶角相等、等量代换，找到一组内错角相等，从而使问题获解.

途径二：利用垂直、等式的性质

例2如图2，已知BA⊥DA于A，CD⊥AD于D，∠1=∠2，那么直线AE、DF平行吗？为什么？

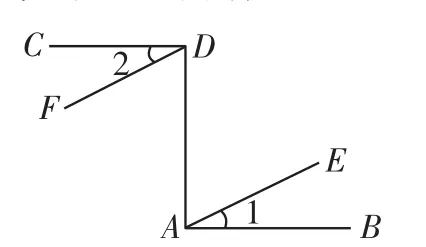
图2

分析：直线AE、DF被DA所截，图中有内错角，如果内错角相等，那么两直线就平行，所以我们要想办法判定直线AE、DF被DA所截形成的内错角是否相等.

解：AE与DF平行.理由如下：

因为BA⊥DA，CD⊥AD，

所以∠BAD=∠ADC=90°.

又因为∠1=∠2，

所以∠BAD-∠1=∠ADC-∠2，

即∠DAE=∠ADF.

所以AE∥DF（内错角相等，两直线平行）.

点评：寻找图中可推出直线平行的内错角或同位角，这是逆向思维的运用.根据垂直定义，可以得到一对相等的角，再加上已知∠1= ∠2，利用等式的性质，可得到一对内错角相等，从而得到两直线平行.

途径三：利用等角、角平分线定义

例3如图3，已知B，D，E三点在一条直线上，∠ABD=∠CDE，BF平分∠ABD，DG平分∠CDE，那么直线BF与直线DG平行吗？为什么？

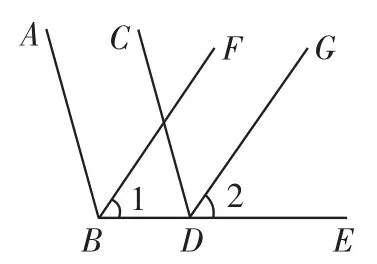
图3

分析：直线BF与直线DG被BD所截，如果同位角相等，两直线就平行，所以要判定这两条直线是否平行，就要转化为判定同位角是否相等，如相等就平行，如不相等就不平行.

解：BF与DG平行.理由如下：

因为BF平分∠ABD，DG平分

∠CDE，

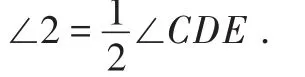
又因为∠ABD=∠CDE，

即∠1=∠2.

所以BF∥DG（同位角相等，两直线平行）.

点评：在几何学习中，常会由已知条件得到多个结论，我们应从中筛选对解题有用的结论.例如，要说明本题的结论，需要知道什么角相等，其余的结论不要注意，以免分散注意力.已知中有∠ABD= ∠CDE，由此条件可得AB∥CD.但对于此题来说这个结论没有用，因此，不要考虑这个结论.

途径四：利用平行线的性质、等量代换

例4如图4，已知∠1=∠2，再添上什么条件可使AB∥CD成立？并就你添上的其中的一个条件说明理由.

图4

分析：若添加能说明同位角相等、内错角相等或同旁内角互补的条件，这样就能用直线平行的判定来说明两条直线平行了.

解：可分别添上以下任意条件：

（1）EB∥FD；

（2）∠MBE=∠MDF；

（3）∠EBN=∠FDN；

（4）∠EBD＋∠FDB=180°；

（5）EB⊥MN，FD⊥MN等.

已知：∠1=∠2，EB∥FD，试说明：AB∥CD.

理由：因为EB∥FD，

所以∠EBM=∠FDM（两直线平行，同位角相等）.

又因为∠EBM=∠1＋∠ABM，

∠FDM=∠2＋∠CDM，

∠1=∠2，

所以∠ABM=∠CDM（等量代换），

所以AB∥CD（同位角相等，两直线平行）.

点评：本题研究直线平行的判定条件，要搞清楚的是添加哪个条件可以得到哪两条直线平行.本题有一定的开放性，回答不同，对应的说理过程也不同.