“数信”整合 自主构建定律模型——《加法、乘法结合律》教学设计

周青燕　谷仁杰

【教学过程】

一、抢答激趣，感受规律

5+12+25+（12+2）

3+25+43+（25+4）

18+35+2518+（35+25）

15+（5+7） 15+5+7

13+（17+3） 13+17+3

利用IRS投票技术，记录学生完成情况，进行口算淘汰赛。

【设计意图：口算淘汰赛是一种较为新颖的口算形式。即利用IRS投票技术，对答案做出选择，答对的同学可以继续答题，答错的同学则被淘汰。显然，这对口算的正确率与速度都有一定的要求。而本节课正好属于计算领域的课程，这样的形式不仅更容易激发学生口算的兴趣与热情，还为教学提供了学习素材。】

二、自主探究，数形建模

1.观察与发现。

师：观察题组，将发现写下来。

2.交流与猜想。

师：谁来分享？谁有补充？

在分享的过程中，教师提炼关键信息，并板书。例如，都是加法算式；加数相同；运算顺序不同；结果相同……

师：那么，满足这些条件的两个算式，结果一定相等吗？

3.举例与验证。

（1）呈现例子：5+12+8○5+（12+8），并猜想。

（2）提出问题：你打算用什么方法来验证呢？

（3）方法交流。

预设方法1：

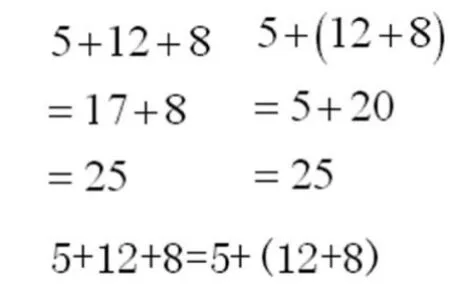
预设方法2：

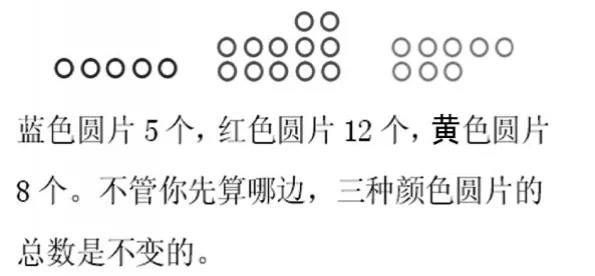
（4）呈现例子，自主尝试。

7+13+6○7+(13+6)

25+1+9○25+(1+9)

（5）你还能举出这样的例子吗？学生自主举例。

（6）交流与演示。

①将例子进行板书后，询问这样的例子举得完吗？

②几何画板动态演示；

③你能想到一个反例吗？针对学生回答，在几何画板上进行即时验证。

4.小结建模。

师：是的，只要满足加数相同，位置相同等条件，改变运算顺序不会影响计算的结果，这就是加法结合律。你能用一个算式来表示吗？（用字母表示）

板书：a+b+c=a+(b+c)加法结合律

5.研究回顾。

师：刚才我们是怎么得到加法结合律的？

板书：观察发现——提出猜想——举例验证——字母表示

【设计意图：本环节旨在让学生经历不完全归纳的推理过程，即观察发现——提出猜想——举例验证——字母表示。从逻辑的维度分析，这样的推理过程应当属于合情推理的范畴，用于发现事实与结论。学生能否掌握这样的推理过程，将一定程度上影响其创新意识与创新能力的发展。但不完全归纳法有其本身的缺陷，学生容易在有限的例子中得出不正确的结论，故笔者利用了几何画板，随意改变数据，形象地演示了大数据的分析，让学生初步体会到只有在大量的例子中，且找不到反例的基础上，得到结论才有一般性。】

三、探究乘法结合律

1.呈现猜想。

师：乘法会有类似的计算规律吗？

2.自主研究。

师：你会怎么去研究？（观察发现——提出猜想——举例验证——字母表示）

师：请你试一试，并把研究过程写下来。

3.小组交流。

呈现合作要求：（1）四人小组轮流汇报，听听伙伴的研究过程合理吗？（2）推选最优方案，准备汇报。

4.汇报交流。

学生汇报交流，教师利用几何画板动态展示。

5.板书提炼。

a×b×c=a×(b×c)乘法结合律

【设计意图：本环节学生通过自主尝试、合作交流等学习活动，再次经历不完全归纳的过程。在小组汇报的过程中，教师应用几何画板的动态演示功能，使学生再次体会到乘法结合律的一般性，从而为突破教学难点再次埋下伏笔。】

四、探究减法，除法结合律

1.呈现猜想。

2.自主尝试，交流反馈。

3.小结。

师：有的同学认为减法和除法也有结合律，也找了大量的例子；但有的同学则认为没有，因为他们找到了很多反例。的确是这样，那么减法结合律和除法结合律到底存在吗？（依旧会有两种声音）其实，我们可以这样想，有一个方法，有时候正确，有时候不正确，那么这样的方法你敢用吗？（都说不敢）所以，减法和除法不存在结合律！

4.反思提炼。

师：为什么加法和乘法有结合律呢？

师：找不到反例，即所有加法算式和乘法算式都适用。

【设计意图：本环节也有自主尝试的安排，但这里学生很快就会发现有反例，故实际需要的时间并不多。本环节的设计，意在让学生理解减法和除法为什么不存在结合律。通过正反对比，相信学生对于律之所以为律一定会有新的感受。】

五、课堂练习，巩固提升

练习1：比一比，看谁算得又对又快。

①43+26+14

②23+37+56

③9×8×5

④25×4×7

⑤225-112-12

⑥144÷12÷12

练习2：用今天学到的本领判断下面结论是否正确。

①a、b、c 表示三个数，则a×b+a×c=a×（b+c）。（ ）

②用 a、b、c 表示三个数，则 a÷b+a÷c=a÷（b+c）。（ ）

【设计意图：习题不多，但都紧紧围绕教学的重难点进行针对性的练习。练习1旨在使学生在巩固加法、乘法结合律的同时，能够进一步感受到学习结合律的价值。同时，通过最后两道易错题的分析，使学生进一步明确减法和除法不存在结合律，需要按照运算顺序从左往右进行计算。练习2旨在巩固利用不完全归纳法来验证结论的方法。】

六、课堂小结，提炼收获

师：通过今天的学习，你有什么收获？

【课后反思】

在运算定律的教学中，一般的教学流程都是：猜想——举例验证猜想——归纳运算定律。这样的教学模式，更多的时候关注的是式子的本身，而并非式子的意义，不利于学生对运算律的内化，构建定律模型。

学生对结合律的认识不是一张白纸。学生对运算定律的理解是建立在加法、乘法运算意义之上，运算定律对运算意义的拓展和延伸，如35+57=57+35，学生一年级就会熟练计算。因此，本节课笔者以信息技术辅助结合律教学，借助数信整合手段,引导学生关注算式意义，自主构建结合律的模型。在课前利用IRS投票技术，全体学生积极参与，充分发挥了信息技术的交互性优势，能及时地反馈教与学的信息，实现师生之间的双向互动交流。在规律探究过程中，利用“几何画板”将大量的数据进行呈现，为学生提供“大数据”的学习素材，引导学生经历大量的直观到抽象的过程，形成运算律模型；引导学生借助几何直观来分析结合律运算规律，关注运算意义的理解。这样教学，打破了原来素材的局限性，丰富了课堂教学内容，启发了学生思维；弥补了教材与传统教学技术的不足，激发了学生的积极主动参与意识。