在“做”中实现数学知识的“再创造”
2016-04-02罗燕斌
罗燕斌
数学学习过程是学生“再创造”的过程。著名数学教育家弗赖登塔尔反复强调:学习数学的唯一正确的方法是实行“再创造”,也就是将要学的知识交给学生,让他们自己去发现或创造出来。在教学中,我们要给学生提供“做”数学的机会,让学生经历数学知识的“再创造”过程,通过自己的实践活动来加深理解,获得知识,提高能力。
一、在“做”中实现数学概念的“再创造”
数学概念是揭示现实世界空间形式与数量关系本质属性的思维形式。客观事物通过人的感官形成感觉、知觉,经过比较、分析、综合、抽象、概括,进而形成概念。在概念教学中,教师完全可以摆脱讲述式的教学方式,也不需要让学生背诵概念,一个新知识是由学生通过自己的思维和“数学现实”建构形成的,这时教师便无须过多地讲解,学生也可以理解掌握。
因此,在进行概念教学时,教师要做的是提供给学生足够丰富的材料,尽量提供“做”的机会,让学生实现数学概念的“再创造”。
以“分数的初步认识”这一课为例,我在教学时,请学生用准备的纸片折出,并画上斜线,学生纷纷动手折折画画。学生展示出了四种不同的折法。
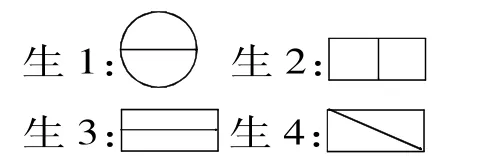
再如:在教学六年级“比例尺”这一内容时,我设计了这样的学案:学校操场有一条80米长的跑道,请你把这条跑道画在练习纸上。学生画完后,让学生说一说你是怎样画的?学生有的说:我把实际的跑道缩小到原来的。有的说:我缩小到原来的。还有的说:我画的长度与跑道实际的长度的比是1∶1000。接着,我又提出:老师带的这块手表,其中一个小零件的长度是0.3毫米,请你把它的长度画出来。学生根据刚才的经验,感到太短了,实在画不出。经过思考,学生把实际零件的长度扩大后画在纸上。有的同学把实际的长度扩大10倍,有的扩大20倍……,还有的说:我画的长度与实际零件的长度的比是10∶1。以上都是学生自己根据实际的需要,运用一定的比,将实际的长度经过扩大或缩小画在纸上。在这个过程中,学生已经在自觉和不自觉中运用“比例尺”解决问题,此时教师揭示“比例尺”的概念已经是水到渠成:像这样图上距离与实际距离的比就叫做这幅图的比例尺。
教师在教学中要多给学生提供“做”的机会,让学生在“做”中对数学概念进行“再创造”,从而大大加深学生对概念的理解,降低学生对抽象概念的学习难度。
二、在“做”中实现数学规律的“再创造”
数学定理和公式是从现实世界空间形式与数量关系中抽象出来的。教师在引导学生正确理解和应用定理、公式的同时,还要设法让学生亲身体会定理、公式的发现过程以实现数学知识的“再创造”。
在教学中,再现知识技能的形成过程,发现数学规律,教师不是把现成的结论灌输给学生,而是提供“做”的机会,指导学生创造性地学习,在操作中发现规律,形成科学的认识,让学生体验数学规律再创造的过程。
教学“三角形的面积”时,不是把“底×高÷2”这个现成结论告诉学生,而是创设情境,让学生在“做”中经历三角形面积计算方法的推导过程。首先让学生利用手中的三角形,拼接一个含有长方形、正方形、平行四边形的小房子平面图,在操作中,学生们发现两个完全一样的三角形可以拼成一个长方形、正方形或平行四边形。同时,经过观察、分析、发现,一个平行四边形相当于两个完全一样的三角形的面积,三角形的底相当于平行四边形的底,三角形的高相当于平行四边形的高,从而进一步推导出三角形的面积计算公式。有了这样的经历,学生在计算三角形面积时就不会忘记“除以2”了。
再如:教学圆锥体积时,传统教学是教师做实验学生看,教师的体验一次次加深,学生却是间接地看,一次次记忆,将公式装进大脑。我在教学时,为每组学生准备了一套学具(一个圆锥、一个圆柱、一盆沙子),让学生把盛满圆锥容器的沙子倒向等底等高的圆柱形容器,反复实验。结果发现,等底等高圆柱体容器盛的沙子总是圆锥体的3倍,从而推导出圆锥体体积的计算方法。
学生有了“做”的机会,经历了数学规律再创造的过程,不仅理解了数学规律,同时也提高了动手能力、观察能力、分析能力和抽象概括能力。
三、在“做”中实现解题方法的“再创造”
“问题”是数学的心脏,所以解题教学自然也是数学课堂教学的核心内容,学生所学的数学知识要在解题过程中进行巩固和应用,一些数学学习的方法和能力也要在解题过程中进行培养。所以,我们要充分利用解题教学来培养学生的“再创造”意识,让他们逐步掌握创造性学习的方式,养成创造性的思维习惯。
在教学中要为学生提供足够的时间和空间,为学生提供“做”的机会,同一道习题从不同角度去分析、思考,提高解题能力。
学校买来科技书和故事书共270本,科技书和故事书本数的比是4∶5,科技书买来多少本?
(2)归一法:270÷(4+5)×4=120(本)
(4)方程法:解:设每份为x本,则:
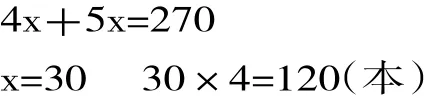
设科技书为x本,则:
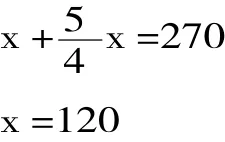
设故事书为x本,则:
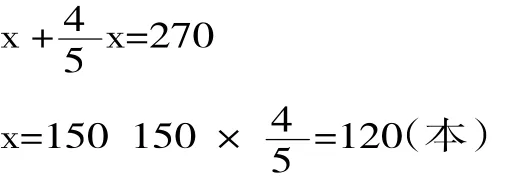
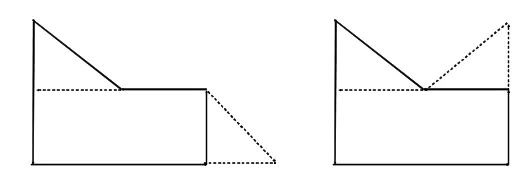
再如下面的一道求组合图形的面积:
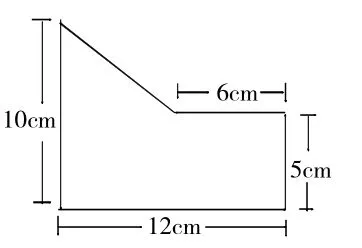
经过几分钟的思考,学生用不同的方法,将组合图形转分为已知图形,找到了九种解决问题的办法。
(1)分割法。
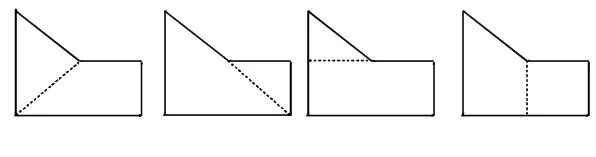
(2)补形法。
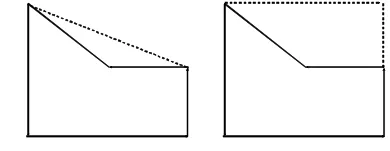
(3)平移法。
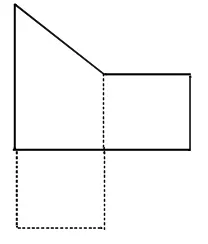
(4)平移、旋转法。
学生有了这样的经历,有了这样的经验,在面对新问题时就不会束手无策,根据自己经验的积累,发挥他们的智慧和潜能,实现解题方法的“再创造”。
数学学习过程是学生“再创造”的过程,在这个过程中学生应始终积极地参与这个活动,感觉到创造的需要,才有可能进行“再创造”。教师的任务就是为学生提供广阔的天地,听任各种不同思维,不同方法的自由发展,让学生“在游泳中学会游泳”,让学生在“再创造”中“创造”数学、学习数学。
