改编例题 精彩不断
2016-03-30杨昌义
杨昌义
改编例题精彩不断
杨昌义

湘教版数学教材七年级下册中安排了这样一道例题:如图1,AB椅DC,蚁BAD= 蚁BCD,那么AD椅BC吗?学生由于刚刚才学平行线的性质和判定定理,对公理化证明方式还只是初步接触。可能为了减少难度,教材事先已连好了对角线AC,把思维直接固定在用“内错角相等,两直线平行”这一条思路上,但这样不利于学生发散思维的培养。为此,笔者上课时去掉了对角线AC,让学生自由发挥。下面再现课堂情景。
上课伊始,教师出示题目:如图2,AB椅DC,蚁BAD=蚁BCD,那么AD椅BC吗?随即引导学生思考——
师:同学们,我们已学了3种平行线的判定方法,分别是哪3种?
生:方法1,同位角相等,两直线平行;方法2,内错角相等,两直线平行;方法3,同旁内角互补,两直线平行。
师:答得非常好!那么,你们怎么应用这些方法判定题目中的AD椅BC呢?
生:图中没有同位角,也没有内错角,显然,方法1、2都不能用,看来只有用方法3了。

图1

图2
师:分析得有道理。但用方法3,必须找到相对应的同旁内角。与AD椅BC相对应的同旁内角有哪些?
生1:与AD椅BC相对应的同旁内角是蚁ABC与蚁BAD,因为它们是直线AD、BC被直线AB所截出来的。
生2:还有蚁BCD和蚁ADC,但只要推出一对角相等就行了。
师:不错!结合已知条件,能推出吗?
生3:由AB椅CD可得蚁ABC+蚁BCD=180毅,两直线平行,同旁内角互补。
师:这两个角互补又有什么用?
生4:有用!因为已知蚁BAD=蚁BCD,由等量代换得蚁ABC+蚁BAD=180毅,于是,由方法3可得AD椅BC,很简单!
师:数学就是很奇妙,你如果知道结论了,就会觉得很简单。而开始不知道的时候,却吸引你去苦苦探究。一旦突破了,心里会有一种特别的舒畅和愉快感,让人回味无穷,这就是数学的魅力!
生5:几何比代数有趣多了!
师:其实数学都有趣,无论是代数还是几何,只要我们进了它的门槛,就是迈进了瑰丽的“万花筒”,里面精彩不断,奥妙无穷!比如,对于上面这题,只要发挥我们的聪明智慧,还是可以应用方法1、2解答的!
生6:不是没有内错角、同位角吗?
师:我们可以想办法构造出来。可以连结BD,内错角是不是就有了?
生6:可以这么做吗?
师:完全可以!为了做题的需要,有时需要作一些线,这种补作的线叫做“辅助线”,一般用虚线画,它能辅助我们完成做题任务。例如,作出辅助线BD(如图3),我们马上得到了内错角,同学们能找出几对?生(齐):两对:蚁ADB和蚁CBD,蚁ABD和蚁CDB。师:与将要证明的AD椅BC有关的是哪一对?为什么?
生7:蚁ADB和蚁CBD。因为它们是直线AD、BC被直线DB所截出来的。
师:回答得非常正确!只要它们相等,由方法2就可以立即得到AD椅BC。那么我们怎么通过条件得到蚁ADB=蚁CBD呢?
生8:由已知AB椅CD,得到蚁ABD=蚁CDB。已知蚁ABC=蚁ADC,由等式的性质得蚁ABC原蚁ABD= 蚁ADC原蚁CDB,于是可得蚁CBD=蚁ADB。
师:你简直太有才了!
生8:这归功于辅助线,非常有用!但我不知道什么时候要作辅助线,也不知怎么作。
师:当题目条件不够时,可以考虑作辅助线,一般有规律可循。有时一道题作的辅助线并不是固定一种,只要对做题有用,都是可以灵活作出的。
生9:那么此题我不连结BD,连结AC(如图4)行吗?
师:你们想想看,行吗?
生10:当然行,只要能得出蚁DAC=蚁ACB。
师:有道理!已知蚁ABC=蚁ADC,那么蚁BAC= 蚁ACD吗?
生11:相等!因为已知AB椅CD,两直线平行,内错角相等。
师:在吟ABC和吟ADC中,已有两对内角相等了,第三对角难道不等吗?
生12:相等!三角形内角和是180毅,小学已学了。
师:现在问题不是也解决了?
生13:辅助线真妙啊!

图3
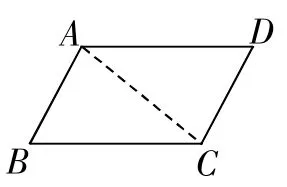
图4
师:更妙的还在后面呢!如果我们再仔细思考,这道题还能用方法1解答呢!生14:还能用方法1?同位角没有,怎么做呢?师:为什么不请辅助线帮忙呢?比如,延长BC……
生14:也可以这么作吗?
师:可以!只要对我们有用,怎么作都行!大家想想,延长BC 至E(如图5),有用吗?
生15:有用!只要我们能够证明蚁ADC=蚁DCE即可。
师:请大家探究:蚁ADC=蚁DCE吗?
生16:已知蚁ADC=蚁ABC,只要得出蚁ABC= 蚁DCE,用等量代换即可。
生17:蚁ABC=蚁DCE,这是明摆着的,因为已知AB椅CD,同位角相等的呀!
师:不是又成功了吗?生18:真是妙不可言!师:大家再想想,我们是否还能在不同位置、不同方向作辅助线呢?
生:老师,我们作出来了,不知行不行,请您检查下(如图6所示)。

图5
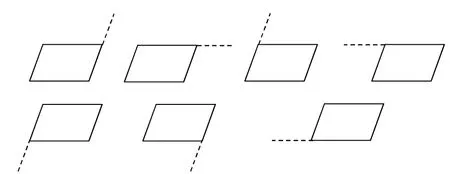
图6
师:太棒了!真是精彩纷呈,美不胜收啊!告诉大家,这些作法都行!像刚才探究的一样,能不能化成用方法1解答?课后同学们可以试试。
教学后记:一题多解对于训练学生的发散思维,培养学生的创新意识十分有益。在本案例中,教师首先让学生明确判定两直线平行的基本方法,然后围绕问题的结论,引导、启发学生如何选择方法,师生共同历经了探究的全过程。师生不断地互提问题,并通过提问使探究活动步步推进、环环相扣。尤其是教师不失时机地介绍了添作辅助线的方法,让学生感受到辅助线在说理中的巧妙作用,激发了学生的兴趣和潜在的创新精神。这样教学,不仅让学生顺利地解答出问题,还渗透了化归思想和“执果索因”的说理方法,也培养了学生的发散思维和演绎推理能力。
(作者单位:永州市零陵区永州柳子中学)
探索
