在探究中构建关系模型

周信国　李海东

关系模型就是表示数量之间关系的模型。小学数学中常见的数量关系包括速度、时间和路程关系，单价、数量和总价关系，工作时间、工作效率和工作总量关系，正比例关系和反比例关系等。如果学生能熟练应用这些数量关系解决实际问题，他们的学习就会事半功倍。因此，教师要注重引导学生自主建构数量关系模型。江苏省优质课比赛一等奖获得者顾宪聪老师执教的“常见的数量关系”为我们做了很好的示范。他大胆放手，引导学生用数学眼光寻找数量关系，分析数量关系。学生在观察、比较和归纳活动过程中理解并掌握了数量关系，自主构建了数量关系的模型，发展了数学思维，提升了数学探究能力。顾老师的课堂幽默、风趣、富有感染力，整节课洋溢着浓浓的数学味。

一、初步探究中构建关系模型

师（出示情境图）：你能很快整理出图中的条件吗？

生：把钢笔买几支和每支几元放在一起，把5本练习本和每本3元放在一起，这样整理才有条理。

师：每支12元可以写成12元/支，读作十二元每支，它表示什么意思？

生：一支钢笔12元。

师：你能把每本3元写成这样的形式吗？

生：3元/本，表示1本练习本3元，读作三元每本。

师：经过整理，你能很快求出什么问题？

生：买钢笔要12×4=48元，买练习本要3×5=15元。

师：你是怎样想的？

生：每支钢笔12元，4支就是4个12；每本练习本3元，5本就是5个3。

师：如果文件夹的价钱是4元/个，想买2个文件夹。老师要问什么问题？

生：文件夹要多少钱？

师：这儿的12元/支、3元/本、4元/个，我们都可以称为商品的单价。

师：买的4支、5本、2个叫作——

生：数量。

师：买每种文具一共用的钱数其实就是——

生：总价。

师：怎么求总价？

生：数量×单价=总价。

师：求钢笔总价是用钢笔单价乘以钢笔数量，那么求练习本的总价呢？

生：练习本的单价×练习本的数量=练习本的总价。

师：文件夹呢？

生：文件夹的单价×文件夹的数量=文件夹的总价。

师：关于这三个数量之间的关系，你还想到了什么？

生：总价÷数量=单价。

师：能结合这里的例子说一说吗？

生：练习本一共要15元，练习本的单价是3元，用练习本的总价÷单价=数量。

师：已知三个量中其中的——（两个）就可以求出——（另一个量）

师：像单价的这种表示形式在生活中还有很多。看！水果店中奇异果的单价是——

生：4元/个。

师：牛肉店里五香牛肉的单价是——

生：20元/盒。

师：茶餐厅中香蕉奶昔的单价是——

生：32元/份。

师：选一个你最感兴趣的单价介绍一下。

生：五香牛肉的单价是一盒20元。

师：如果买2盒五香牛肉，总价是多少？

生：20×2=40（元）。

师：如果买3盒呢？

生：20×3=60（元）。

师：现在想买5盒呢？

生：5×20=100（元）。

师：可以写成20×5吗？

生：可以。

师：看这些算式——20×2=40（元）、20×3=60（元）和20×5=100（元），你有什么发现？

生：都是单价×数量=总价。单价不变，数量变，总价跟着变。

师：如果现在老师想买2个奇异果、2盒五香牛肉和2份香蕉奶昔，谁的总价最多？为什么？

生：香蕉奶昔单价是32元/份，单价最大。它们的数量一样，单价越大，总价越多。

【赏析】数学来源于生活。在教学中，顾老师引导学生用数学眼光观察生活中购物的实际问题，在初步认识单价后，引导学生学会改写单价、读出单价，然后学生根据已知条件提出问题，再在问题解决中认识数量和总价后，直至自主发现“数量、单价和总价”三者之间的关系，构建“数量×单价=总价”的计算模型，并举一反三地发现“总价÷数量=单价”以及“总价÷单价=数量”。三个数量中，最核心、最重要的是单价，顾老师通过奇异果、五香牛肉和香蕉奶昔等商品信息帮助学生进一步认识单价，促进学生在随机应用中进一步理解并掌握“数量×单价=总价”这个基本数学模型。学生在模型构建中不但发现了积的变化规律（单价不变，数量变，总价跟着变），而且初步感悟了模型思想和变与不变的数学思想，还在分析和对比中梳理了“数量、单价和总价”三者之间的关系，增进了学生对数量关系的认识，增强了学生数学学习中的探究意识和模型意识。

二、深入探究中构建关系模型

师：老师从南京开车来学校，每小时行90千米；徐老师骑自行车来学校，每分钟行200米。这些都可以称为速度。2小时、10分钟就是——

生：时间。

师：一共行多长的路就是——

生：路程。

师：速度在生活中很常见，举个例子吧。

生：徐老师骑车每分钟行200米就是速度。

生：顾老师开车每小时行90千米也是速度。

师：乌龟的速度是每分2米，可以改写成2米/分；声音的速度是每秒340米，能改写吗？

生：340米/秒。

师：表示什么意思？

生：声音的速度是每秒340米。

师：真好。还能说说其他速度吗？

生：公路限速120千米/时。

生：一辆汽车的速度是100千米/时。

师：当前的速度是100千米/时。如果一辆车行驶在这条路上，超速吗？

生：不超速。

师：像这儿的每分、每秒、每时行的路程，我们都把它称为——

生：速度。

师：速度、时间和路程三者之间有什么关系？

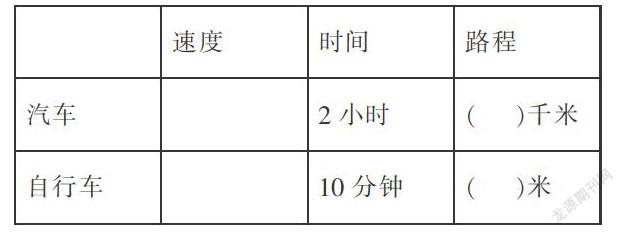
（课件出示研究提示：1.写：把速度改写成另外一种形式；2.算：分别求出汽车和自行车行驶的路程；3.想：速度、时间和路程之间有什么关系？学生完成后展示交流。）

生：汽车速度是90千米/时，自行车速度是200米/分。

师：表示什么意思？

生：90千米/时就是汽车行90千米要1小时。

生：汽车速度90千米/时×时间2时=路程180千米；自行车速度200米/分×时间10分=路程2 000米。

师：你发现了——

生：路程=速度×时间。

师：感谢你们帮老师算出南京到江阴的路程是180千米。如果现在老师改骑摩托车，需要多少时间？（出示：摩托车速度是60千米/时。）

生：180÷60=3（时）。

师：如果以后从南京到江阴开通动车要多少时间？（出示：动车速度是180千米/时。）

生：1个小时。

师：怎么求时间？

生：路程÷速度=时间。

师：如果要求速度呢？

生：路程÷时间=速度。

师：你还有什么发现？

生：动车最快，摩托车最慢。

生：路程不变，速度越快，时间越少。

师：说得真好。随着交通工具的发展，速度越来越快，时间却越来越少。这三者之间的关系有没有变？

生：没有，都是路程=速度×时间。

【赏析】路程、时间和速度三个数量中，速度是核心。顾老师先根据实际情况引导学生初步认识速度、时间和路程，学习速度的改写、读法和意义，接着引导学生认识“超速”，再引导学生通过自主写、算、读和交流，合作发现了这三种数量之间的关系——“路程=速度×时间”“路程÷速度=时间”“路程÷时间=速度”，从而建立了三个新的数学模型。学生在构建数学模型的过程中发现“路程不变，速度越快，时间越少”的规律，但三者之间的关系不变，都是“路程=速度×时间”。把实际问题抽象成数学模型的过程中，学生不仅深刻理解了速度的内涵，还理清了路程、速度和时间之间的数量关系。鲜活、多样、由浅入深的探究练习，不仅帮助学生在解决简单实际问题中进一步理解并掌握了所建构的数学模型，而且帮助学生在建模活动中体会到数学学习的价值，感知了联系和发展的观点，进一步感悟了数学模型思想和变与不变的数学思想。

三、沟通联系中深化关系模型

师：总价=单价×数量、路程=速度×时间，都是我们生活中常见的数量关系。能不能用自己的方式表示这两个数量关系呢？

生：总数=每份数×份数。

师：这儿的每份数、份数和总数指什么呢？

生：总数在这儿指总价，每份数指单价，份数指数量。

生：每份数×份数=总数。总数就是总价和路程，每份数就是单价和速度，份数就是数量和时间。

师：真厉害，把两个都说进去了。

师：你能编一道关于总价、单价、数量或者路程、速度、时间的数学问题吗？

生：买一个杯子要10元，买3个杯子一共要多少钱？

师：谁能回答？

生：三个杯子一共要30元。一个杯子10元，3个杯子就是3个10，用乘法算。

师：用的什么数量关系？

生：单价×数量=总价。

生：买3瓶可乐，每瓶要3元。一共要多少元？3×3=9（元）。

师：用的是什么数量关系？

生：单价×数量=总价。

生：一辆动车每小时能行300千米，行了3小时。行了多少千米？每小时行300千米，行了3小时，3个300，就是900千米。

师：用了什么数量关系？

生：速度×时间=路程。

【赏析】数学模型最重要的作用就是用数学语言解释现实世界。史宁中教授认为，在小学数学“数与代数”部分，本质上只有“总量=部分量+部分量”和“总数=每份数×份数”两种模型。从这种意义上说，学生所发现的数量关系其实是乘法意义的一种具体化。在教学中，顾老师引导学生尝试用自己的话总结数量关系式与乘法意义的联系，沟通了数量关系之间的联系。学生把两个似乎不同的数量关系融为一体，从而使所学知识真正具有了数学模型的价值。编题不仅培养了学生的数学语言表达能力，而且培养了学生应用数学模型的能力。学生在应用中不仅加深了对所构建模型的理解和认识，而且在加深理解中内化了数学模型。

整节课，顾老师把教学重点放在“数量关系”的教学上，通过呈现数学味的现实情境，引导学生经历知识的“生长”过程，促使学生在现实背景中和问题解决过程中，透过现象看本质，发现数量之间的内在联系，体会和抽象出数学模型，探索了更深层次的数学规律，提升了学生的综合数学素养。