独立性与相关性判别的一些注记及应用
2016-03-23范国良陆晓恒
范国良陆晓恒
(1. 安徽工程大学, 安徽 芜湖 241000;2. 铜陵学院, 安徽 铜陵 244000)
独立性与相关性判别的一些注记及应用
范国良1陆晓恒2
(1. 安徽工程大学, 安徽 芜湖 241000;2. 铜陵学院, 安徽 铜陵 244000)
从两个随机事件的独立性出发,引入两个随机变量的独立性与相关性的概念,给出独立性与相关性的一些常见判别方法及注记,通过实例说明使用密度函数判别独立性有出错的可能,进而给出使用密度函数判别独立性的一个充要条件,以避免判别错误的发生。最后用一些实例说明独立性与相关性在实际生活中的应用。
随机变量;独立性;相关性;正态分布
独立性是概率论中最基本的概念之一,无论在理论研究还是在实际应用中都有特别重要的意义。概率论与数理统计中的许多成果都是在某种独立性的前提下得到的,因而研究如何判断随机变量的独立性显得尤为重要。
一、独立性
(1)两个随机事件的独立性
两个事件的独立性是指一个事件的发生不影响另一个事件的发生。这在实际问题中是很多的。比如在抛2枚硬币的实验中,记事件A为“第一枚硬币是正面”,B为“第二枚硬币是正面”,显然A与B的发生是互不影响的。从概率的角度看,给定事件A的条件概率P(A|B)与无条件概率P(A),若事件A与B的发生是互不影响的,则有
P(A|B)=P(A),P(B|A)=P(B)
上述两式又都分别等价于P(AB)=P(A)P(B)。
定义 对任意两个随机事件A与B,若有P(AB)=P(A)P(B)成立,则称事件A与B相互独立,否则称A与B不独立。
在随机事件独立的基础上,接下来引入随机变量的独立性。
(2)两个随机变量的独立性
定义:设X,Y是两个随机变量(r.v),若对任意的x,y,有
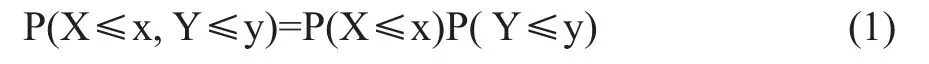
则称随机变量X和Y是相互独立的。
注1 随机事件的独立性是随机变量的独立性的本质。
注2 由于F(x,y)= P(X≤x, Y≤y),Fx(x)=P(X≤x),Fy(y)=P( Y≤y),上述定义用分布函数表示即为:若对所有实数 ,有:则称随机变量X和Y是相互独立的。

(2)式表明,当两个随机变量相互独立时,它们的联合分布函数等于两个边缘分布函数的乘积。(2)式把随机变量的概率关系转化为函数关系,而函数关系的判别一般来说会容易些。
注3 (充分条件)设(X,Y)是连续型r.v.,f(x,y)是(X,Y)的联合概率密度,fx(x),fy(y)分别是X和Y的边缘概率密度。若对所有实数x,y,有:
f(x,y)=fx(x)fy(y)
则随机变量X和Y是相互独立的。
注3 只是判别独立性的充分非必要条件,所以应用时容易在这里出错。我们看下面这个例子。
例1 设二维连续型r.v.(X,Y)在由x轴,y轴及直线所围成的闭区域D上服从均匀分布,试问:r.v.X,Y是否相互独立?
,则X与Y不独立。
原因剖析:二维连续型r.v.在一个点上取值的概率为0,仅仅由一个点处的联合概率密度函数值不等于两个边缘概率密度函数值的乘积,并不能推出(1)式或(2)式,故上面的解法不正确。
注4 (充要条件)若(X,Y)是连续型r.v.,f(x,y)是(X,Y)的联合概率密度,fx(x),fy(y)分别是X和Y的边缘概率密度。若对所有实数x,y,几乎处处有

则随机变量X和Y是相互独立的。
想要证明两个r.v.不独立,只要证明在某个非零测度集上,几乎处处有

由注4,例1的正确解法是:
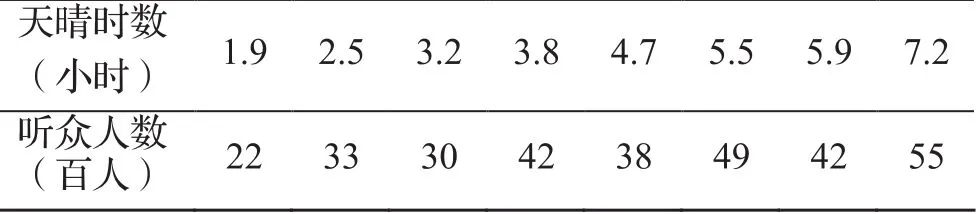
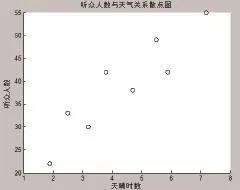
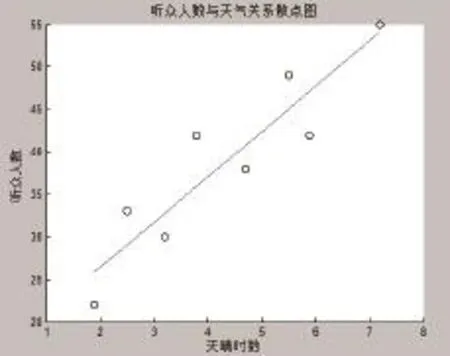
注5 (充要条件)设(X,Y)的联合概率密度f(x,y)(a 例2 设(X,Y)的联合密度函数为: 解:因为x≤y≤2,y的范围与x有关,不是一个常数,故由注5知X和Y不是相互独立的。 注6 若(X,Y)是离散型r.v.,且对(X,Y)的所有可能取值(xi,yj),有: P(X=xi,Y=yj)=P(X=xi)P(Y=yj), 则随机变量X和Y是相互独立的。 定义 称为r.v.X和 Y的相关系数。 相关系数反映了两个随机变量之间的一种联系,若ρXY= 0,则称X与Y不相关。 注7 若两个r.v.X与Y相互独立,则X与Y不相关。 注8 若两个r.v.X与Y不相关,则r.v.X与Y不一定独立。 下面这个例题可以清楚的展示上面的结论。 例3 已知r.v.X的分布律为:判断r.v.X与Y是否相互独立?是否相关? 解 由于Y=X2,Y=X2,Y的值完全由X决定,故X与Y不独立。 注9 若随机变量(X,Y)服从二元正态分布N(a,b,σ ,σ ;r),则下列三个命题是等价的:(1) 2212 X与Y相互独立;(2)X与Y不相关;(3)r=0。 证明 由于独立一定不相关,故(1)→(2)成立。又由定义立得(2)→(3)成立。下面证明(3)→(1)成立。当r=0时,立得(X,Y)的联合密度等于两个一元正态分布边缘密度的乘积,由注5,有X与Y相互独立,即(3)→(1)成立。 下面通过几个例子来展示相关性与独立性的实际应用。 例4 Head First健生俱乐部为自己能为每一位前来健身的人找到合适的班级感到自豪。这正是俱乐部风靡老中少健身者的原因。健身俱乐部目前正在动脑筋,为的是最有效的推销它新开设的瑜伽班。他们想知道,是否参加游泳班的人更有可能参加瑜伽班。他们中有人提出“也许我们给游泳班的学员一些折扣,鼓励他们参加瑜伽班。” 首席执行官不同意,“我想你们错了”,他说,“参加游泳班的人和参加瑜伽班的人是相互独立的,我不认为参加游泳班的人比其他人更有可能参加瑜伽班”。 他们调查了96人,问他们是否参加游泳班或瑜伽班。在这96人中,有32人参加瑜伽班,72人参加游泳班,有24人最积极,两个班都参加了。 那么,谁对谁错?瑜伽班和游泳班,是相关还是相互独立? 分析 记A表示参加瑜伽班,B表示参加游泳班,则发现P(AB)=P(A)P(B),故参加游泳班的人与参加瑜伽班的人是相互独立的,首席执行官是对的。瑜伽班和游泳班是不相关的。 例5 相关还是独立? 1. 在星期二(已知条件)下雨。 独立。不会由于是星期二而更有可能下雨或不下雨,因此二者是独立事件。 2. 从抽屉里拿袜子,直到拿出一双。 相关。在取出一只袜子后,下一次取袜子时,原来的袜子数就减少了,这会影响概率。 3. 从一盒巧克力中随机拿巧克力,连续2次拿到黑巧克力。 相关。巧克力盒子中有黑、白巧克力,在第一次拿到黑巧克力后,黑巧克力减少一个。 例6 某部门承接组织一场商业性露天音乐会,遇到天气变化,该部门希望能够根据预计天晴时数(小时)预测出音乐会的听众人数,这样一来,他们就可以衡量阴天可能给听众人数造成的影响。若听众人数少于3500人,这时票房收入将无法抵消成本费用,那么他们就取消音乐会。下面是样本数据。 能否根据这组数据判断露天音乐会听众人数与当天预计天晴时数之间的关系。 解 先根据样本数据画出散点图,见左边,右边是一次曲线拟合图。 图1 样本数据的散点图 图2 一次曲线拟合样本数据图 从图1中可以看出,数据点在图上呈直线分布,且这条线随天晴时数增加而向上爬升。故可画一条穿过这些点的直线y=a+bx,使这条线尽量接近各个点,见图2。由最小二乘法可得:a=15.80,b=5.32。 于是,听众人数和天晴时数之间的关系接近y=15.80+5.32x,听众人数和天晴时数是相关的。接下来计算对应的相关系数: 由于r接近于1,说明听众人数和预计天晴时数之间有很强的正线性相关性。 随机变量的相关性和独立性是随机变量的两个最重要的关系,而不相关是不独立的一种特殊关系,在判别随机变量是否独立时,要注意两个随机变量不相关,二者不一定独立。另外联合概率密度等于边缘概率密度乘积只是判别随机变量是否独立的一个充分条件,而非充要条件。若两个随机变量服从二维正态分布,则独立和不相关是等价的。 [1]魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,1982. [2]复旦大学.概率论基础[M].上海:复旦大学出版社,1979. [3]张宏礼,王苫社,周晓晶,等.随机变量独立性的一个注记[J].高等数学研究2010(13):114-115. [4]金天寿,王晓华,李聪.随机变量独立性的判别方法[J].高等数学研究,2014(17):92-95. [5]金天寿.对事件独立性的再认识[J].数学通报,2012(51):24-26. Some Notes and Practical Applications of Independence and Correlation Fan Guo-liang1, Lu Xiao-heng2 The concepts of independence and correlation of two random variables are introduced from the independence of two random events. Further we give some notes and discriminated methods for judging independence and correlation. By using the density function in general teaching material for judging independence is easy to make mistakes, and we analyze the situation of the mistakes which are easy to make by an example. To solve this problem, we in this paper, give a necessary and sufficient condition for judging the independence via the density function, which can avoid this mistake. At last, some real examples are taken to illustrate the applications of independence and correlation in life. random variable; independence; correlation; normal distribution O211 A 1672-0547(2016)06-0088-03 2016-06-23 国家自然科学基金(11401006) 范国良(1981-),男,安徽黄山人,安徽工程大学数理学院副教授,博士,硕士生导师,研究方向:概率统计; 陆晓恒(1966-),男,江苏苏州人,铜陵学院数学与计算机学院副教授,研究方向:概率统计。
二、相关性
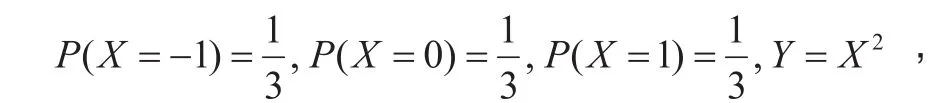
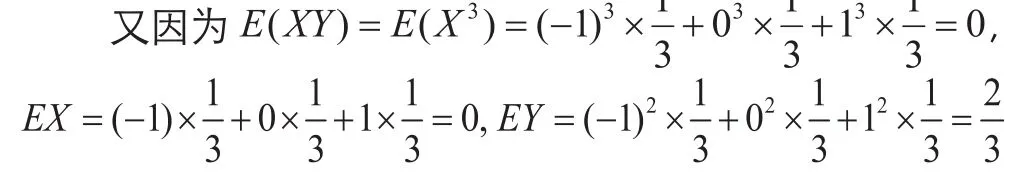
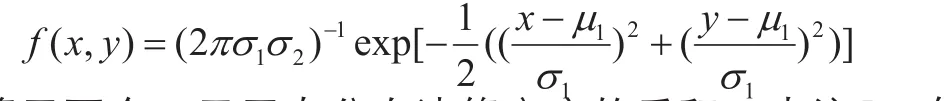
三、应用
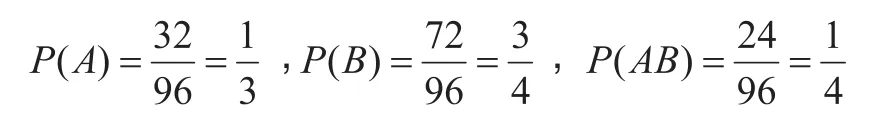
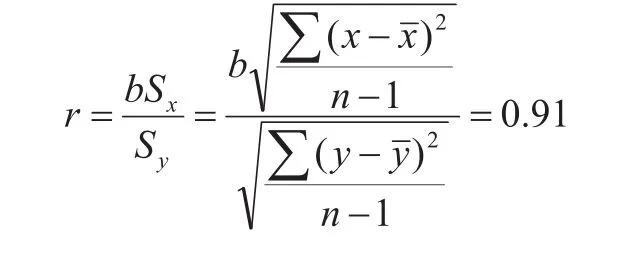
四、结论
(1.Anhui Polytechnic University, Wuhu Anhui 241000, China; 2.Tongling University, Tongling Anhui 244000, China )
