DEM空间尺度对可照时数模拟结果的影响——以浙江省仙居县为例*
2019-04-17赵玉竹
李 军,王 超,赵玉竹
DEM空间尺度对可照时数模拟结果的影响——以浙江省仙居县为例*
李 军1, 2, 3,王 超1,赵玉竹1
(1.重庆师范大学地理与旅游学院,重庆 401331;2.重庆市高校GIS应用研究重点实验室,重庆 401331;3.三峡库区地表过程与环境遥感重庆市重点实验室,重庆 401331)
以浙江省仙居县为实验区,基于4种不同空间分辨率DEM提取相关地形因子,结合可照时数分布式模型,利用数字地形分析和空间数据叠置分析等方法,模拟1月和7月4种空间分辨率下的可照时数,并定量分析DEM尺度效应对模拟结果的影响。结果表明:(1)模拟结果的空间异质性随分辨率减小而减小,其平均值逐渐增加,且1月增幅大于7月,最大值随分辨率的变化不大,而最小值差异较大,标准差逐渐减小。(2)受海拔和地形遮蔽影响,平地和山脊处可照时数最多,海拔200−400m区间最少,400−1100m区域可照时数随海拔增加而增加。以10m分辨率结果为参照,30m、90m和900m分辨率下的差值随分辨率减小而增加,海拔<100m处差值最小,700−900m区域差值最大,1月日均多算0.7、1.4和2.9h,7月日均多算0.5、0.9和2.3h。(3)坡度0−55°范围内,可照时数随坡度增加而减少,30m、90m和900m分辨率与10m分辨率的差值随分辨率降低而增加,且最小差值均在<5°区域,最大差值在不同坡度等级,1月日均多算2.1、1.8和1.7h,而7月日均多算0.3、0.6和1.2h。(4)受太阳高度角和方位角影响,可照时数在南坡−北坡间的差异较大,东南−西南坡、东坡−西坡以及东北−西北坡之间差异较小,30m、90m和900m分辨率与10m分辨率的差值随分辨率降低而增加,在偏北坡,1月差值大于7月,最大差值在1月的北坡上,日均多算1.4、2.5和4.8h,在偏南坡上,1月差值小于7月,最大差值在7月的南坡或西南坡上,日均多算0.5、0.9和2.1h。
山地;可照时数;数字高程模型;尺度效应;空间分布
可照时数(Duration of Possible Sunshine,简称DPS)是指地理可照时数,即考虑地形遮蔽而不考虑大气影响时从日出到日落的全天太阳可能照射时间。它是估算太阳辐射的重要参数之一,已被广泛应用于地表辐射模拟和能量平衡等研究。对于多山且地形地貌复杂地区,由于纬度、海拔、坡度、坡向以及地形遮蔽度等因子的差异,可照时数空间异质性很大,其空间分布研究对于太阳能等气候资源区划及其开发利用、山地生态环境保护等均具有十分重要的意义[1]。
国内学者对可照时数空间分布的研究开始于理论模型,翁笃鸣等[1−5]等自20世纪80年代初陆续提出了不同的理论算法,但受制于计算条件等因素的限制,诸多地理和地形因子的提取只能在小范围借助地形小网格的图解法确定[4−5],数据计算和分析能力十分有限,计算过程繁琐且耗时长,制图效果也差。之后,数字高程模型(DEM)的提出,数字地形分析的广泛应用以及多种高空间分辨率DEM数据的免费获取等,为山地可照时数空间分布研究提供了很好的条件,目前,基于DEM的山地可照时数空间分布模型已经成熟。国外,Dozier[6]在20世纪70年代末首次在地形参数快速算法的基础上提出了基于DEM的太阳辐射空间化方法。之后,Dubayah等[7−10]相继开展了基于GIS的直接辐射、散射辐射、总辐射和可照时数等不同太阳辐射要素的空间分布模拟研究。国内学者在20世纪90年代初开始基于DEM的山地可照时数空间分布研究。李新等[11]修正了基于DEM的日照时数空间分布模拟方法。曾燕等[12]利用1km分辨率DEM数据和基于PCI软件的二次开发程序实现了中国可照时数的空间分布模拟,并探讨了其受不同地形的影响。黄晚华等[13]改进了坡面日照计算模型,并利用模型、Citystar软件和500m分辨率的地形数据,估算了湖南省的年日照时数。李军等[14]以20m分辨率的DEM数据为基础分析了浙江省仙居县可照时数空间分布特征。孙娴等[15]基于100m分辨率DEM数据,考虑了坡度、坡向、地形遮蔽等对可照时数的影响,通过数值模拟确定陕西省山地可照时数计算模型。王怀清等[16]基于1:25万DEM构建了可照时数自动计算模型。近年来,张超等[17]基于DEM实照时数计算模型,以广西省巴马县为例,对实照时数时空分布进行了模拟和验证,采用的DEM是分辨率约为30m的ASTER GDEM。卢燕宇等[18]构建了起伏地形天文辐射模型,并以安徽省为例,对模型进行了参数化和应用。由以往研究可见,在基于DEM的可照时数空间分布模拟中,DEM数据是重要的输入参数,对结果的影响非常显著,然而,由于地形表面特征、空间尺度、DEM结构、内插方法和采样点等原因致使DEM数据存在误差,其中,不同空间分辨率的DEM在很大程度上反映了对真实地形的概括程度,也是山地可照时数模拟中由于其空间尺度效应产生误差的重要根源。DEM的空间分辨率越小,尺度越大,对真实地形的概括程度越低,地形因子的误差越大[19]。目前,基于不同分辨率的DEM分析其尺度效应对可照时数等太阳辐射要素的影响研究报道并不多见,而且,采用DEM的空间分辨率普遍较粗,不能较准确反映山地可照时数的空间异质性[20−22]。
本研究以浙江省仙居县为例,综合考虑目前应用较广泛的DEM数据源、研究区范围大小、数据计算量以及便于模拟结果的定量比较等因素,利用10、30、90和900m共4种不同空间分辨率的DEM数据,模拟起伏地形下不同空间尺度可照时数,并定量分析DEM的空间尺度效应对模拟结果的影响,以期为提高山地可照时数等太阳辐射要素的模拟精度、分析其模拟过程中存在的不确定性、以及山地其它气候要素空间化精细模拟和山地气候资源区划等提供依据和借鉴。
1 资料与方法
1.1 研究区概况
研究区为仙居县,地处浙江省东南丘陵山区,介于28°28′14″−28°59′48″N和120°17′6″− 120°55′51″E。总面积1996km2,其中,山地面积1624km2,约占全县土地总面积的81.4%,属于典型的山区(图1)。
1.2 DEM数据
(1)1:10000的DEM
将仙居县1:10000数字化地形图在地理信息系统软件ArcGIS建立不规则三角网(TIN),并通过空间内插得到10m空间分辨率的DEM(图1),从中提取纬度、坡度、坡向等地理和地形因子空间数据,并将10m×10m网格作为推算可照时数的最小空间单元。
(2)其它3种空间分辨率的DEM
根据研究区边界,分别从目前应用广泛且能免费获取的3种空间分辨率DEM数据库(ASTER GDEM,SRTM和GTOPO30´)中截取,并进行投影转换和重采样等,得到实验区3种空间分辨率的DEM数据,分辨率为30m、90m和900m。
1.3 山地可照时数的分布式模型
根据文献[1−2]的研究结果,起伏地形下可照时数可表示为

(1)水平面可照时数(T0)


(3)地形遮蔽系数(gi)
起伏地形下,一天内某时段i的遮蔽情况取决于该时段内起始和结束两时刻的遮蔽情况,若两时刻均可照,则此时段可照,地形遮蔽系数取1;若两时刻均遮蔽,则此时段遮蔽,地形遮蔽系数取0;若一个时刻可照,另一个时刻遮蔽,则此时段的地形遮蔽系数取0.5。某时刻的地形遮蔽情况可利用ArcGIS中的山体阴影函数(输入坡度、坡向以及某时刻太阳天顶角和太阳方位角)计算得到,其中,遮蔽半径取20km。
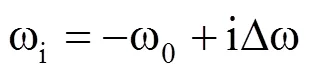

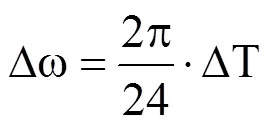


时间步长越短,模拟结果的精度越高,但其计算时间越长。根据李占清等研究,时间步长取20min与1min时的模拟结果仅相差5%[1−2],在考虑数据计算量和模拟结果精度等因素后,将时间步长设为10min。
1.4 可照时数的模拟
以上模型中分别输入4种空间分辨率的DEM和其它参数,利用ArcGIS对空间数据的叠加运算和分析功能等,得到研究区任意一天的可照时数模拟结果,一般将逐日可照时数累加可得到月或年可照时数。为了减少计算量,根据气候学的相关论述[1,3]:取每月第15日为代表日,将每月代表日的可照时数乘以当月天数作为该月可照时数;考虑到冬夏季之间的差异较显著,仅计算1月和7月代表日(第15日和第196日)的可照时数,乘以31得到1月和7月4种不同空间分辨率的可照时数。
2 结果与分析
2.1 DEM尺度对典型月可照时数空间分布的影响
由图2和图3可见,不论1月还是7月,研究区内可照时数分布的空间异质性均随着空间分辨率的减小(10m、30m、90m和900m)而减小,直观上看,10m、30m和90m分辨率下可照时数空间分布有随高度、坡度、坡向等地形因子变化的特征,具体表现为平地和山脊的可照时数多,低海拔的山谷区域可照时数少,且其间差异不明显,而900m分辨率下可照时数的空间分布均已看不出随地形因子变化的特征。图2与图3相比可知,7月可照时数比1月多,空间异质性明显比1月小,说明冬季可照时数受地形影响比夏季显著。
为进一步定量比较不同空间尺度可照时数的差异性,利用ArcGIS的空间分析功能,统计典型月份(1月和7月)4种不同空间分辨率可照时数模拟结果的最小值、最大值、平均值和标准值,结果见表1。由表可看出,无论7月还是1月,随着空间分辨率的减小,可照时数的平均值均逐渐增加,且1月增幅大于7月。进一步分析可见,不同分辨率下模拟的可照时数最大值间基本无差异,主要是由于可照时数的最大值常分布在平地和山顶,说明其对空间分辨率较不敏感。不同分辨率下模拟的可照时数最小值间差异很大,7月可照时数最小值随着分辨率的降低逐渐增加,1月可照时数最小值一直为0,当分辨率降至900m时1月可照时数最小值从0陡增到220.1h,这是因为可照时数最小值常分布在坡度和地形遮蔽度大的区域,而这些地形因子对空间分辨率较敏感。从标准差的比较可见,随着空间分辨率的降低,可照时数模拟结果的标准差逐渐减小,1月减幅大于7月,说明其模拟精度降低、空间异质性变小。

图2 不同空间分辨率下仙居县1月可照时数分布
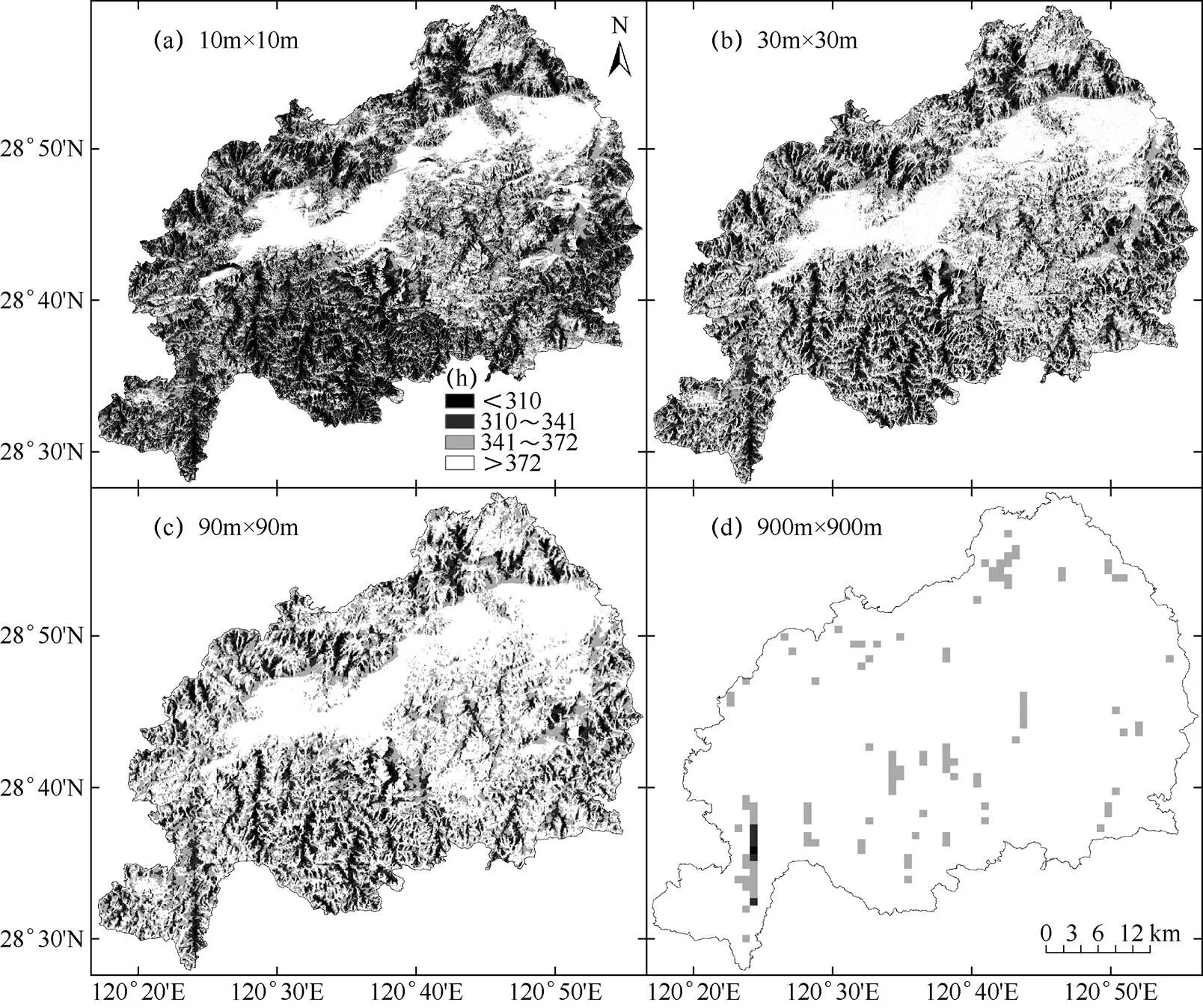
图3 不同空间分辨率下仙居县7月可照时数分布
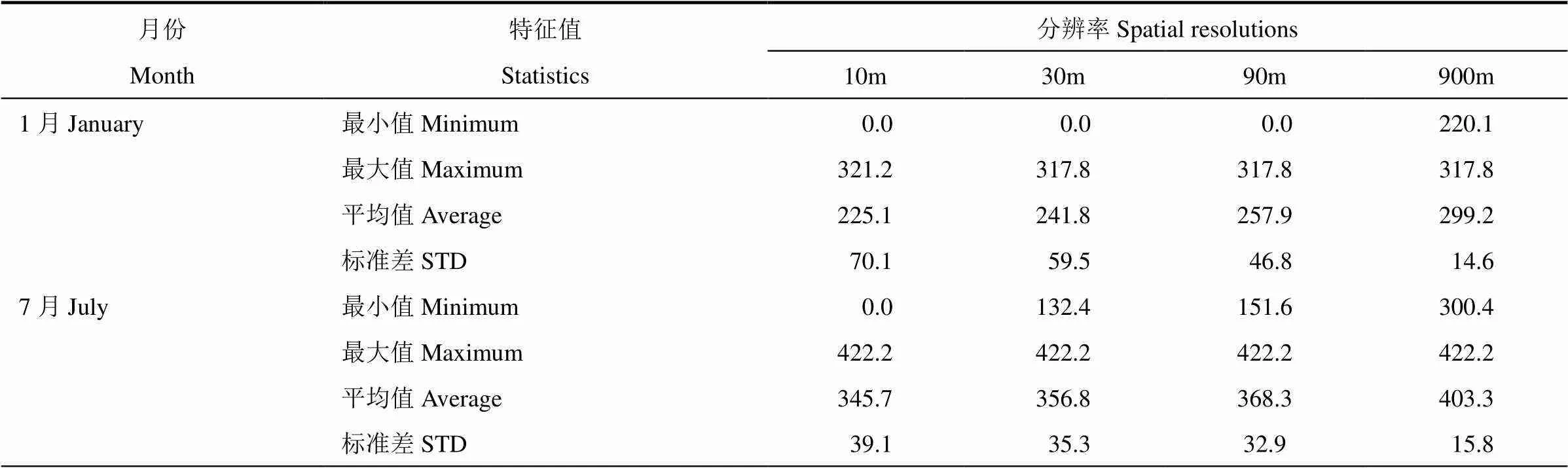
表1 不同空间分辨率下可照时数计算结果的统计特征值(h)
2.2 DEM尺度对典型月可照时数随海拔高度分布的影响
利用ArcGIS的空间分析功能,将海拔高度按每100m分类,大于1100m作为一类,共分为12类进行统计,结果见表2和表3。由表2可看出,基于4种分辨率DEM计算的1月可照时数随海拔高度变化均表现出同样特点:平地(<200m)和山脊(>1100m)最多,200−400m区域由于受地形遮蔽影响最大,可照时数最少,400−1100m可照时数随海拔高度增加逐渐增加。但从具体数值看,不同分辨率间存在一定差异。以10m分辨率的1月可照时数为参照,分别计算30m、90m和900m分辨率时1月可照时数在不同海拔高度上的差值,在海拔<100m的平地区域差值相对较小,高于100m区域差值呈现增加趋势,但无论是哪个海拔高度等级上,各分辨率下可照时数与10m分辨率下的差值均随分辨率的减小而增加。在海拔700−900m区域各分辨率与10m分辨率下的差值最大,30m、90m和900m分辨率时差值分别达到22、42、92h左右,相当于1月日平均可照时数多算0.7、1.4和2.9h。可见,分辨率对除平地外其它区域1月可照时数的计算结果均有明显影响,分辨率越低,这些区域计算的1月可照时数越多,日可照时数可能偏多2~3h。
7月可照时数随海拔高度的总体变化(表3)特点与1月类似,也表现为平地和山脊最多,200−400m区域最少,400−1100m区域随海拔高度增加逐渐增加。各分辨率下可照时数与10m分辨率下的差值在各海拔高度等级上均随分辨率的减小而增加,但差值均小于1月,此外,还存在一些具体的差异,相对1月而言,分辨率对7月可照时数的影响稍弱,与10m分辨率的差值最大也在海拔700−900m区域,其它分辨率的差值分别为15、28、71h左右,日平均可照时数约多算0.5、0.9和2.3h。可见,尽管7月的太阳高度角较高,可照时数受地形遮蔽影响较小,但分辨率对可照时数的计算结果仍有较明显影响,日可照时数可能偏多2h以上。

表2 分海拔高度统计不同空间分辨率的1月可照时数(h)
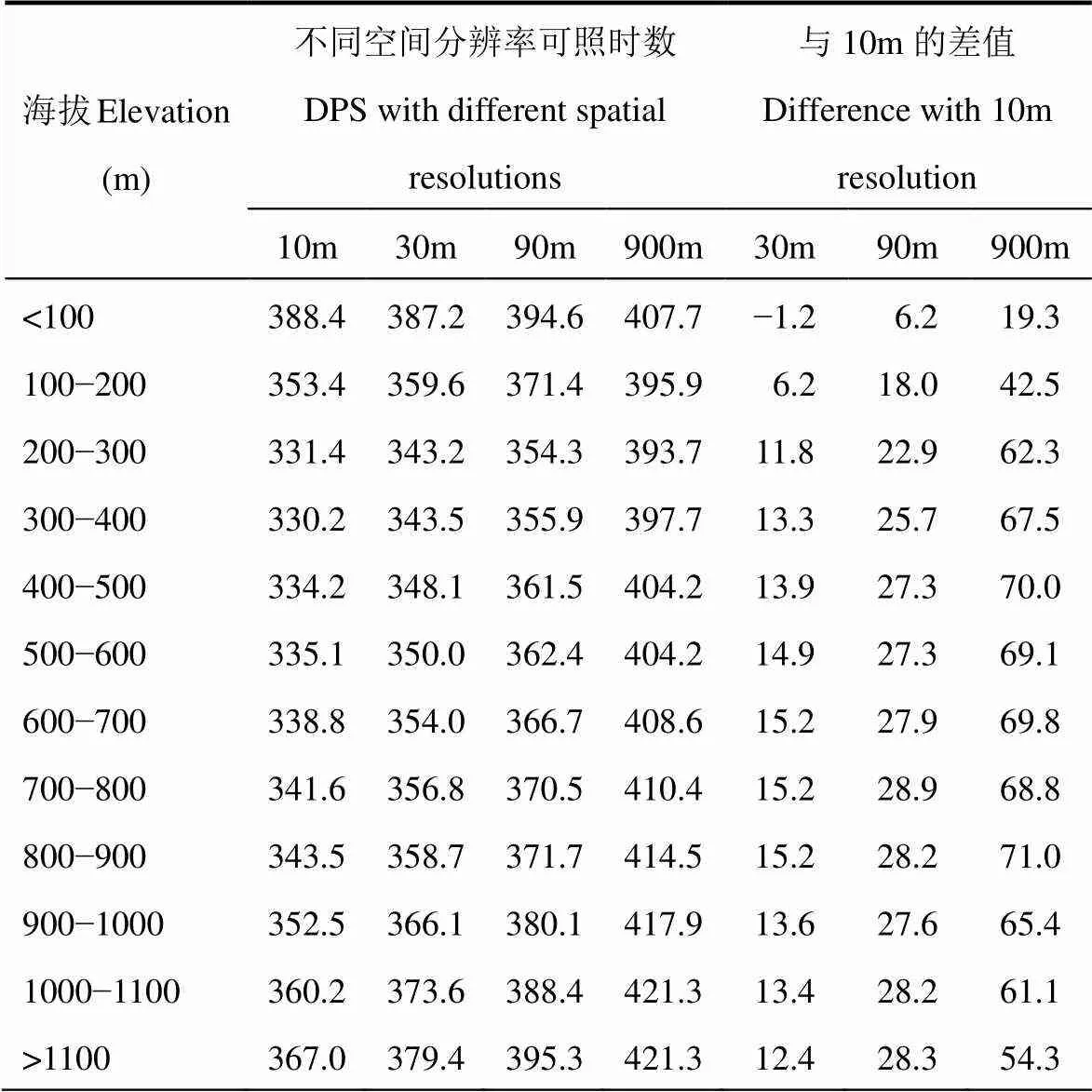
表3 分海拔高度统计不同空间分辨率的7月可照时数(h)
2.3 DEM尺度对典型月可照时数随坡度分布的影响
为了定量分析不同坡度处4种不同空间分辨率下可照时数的差异及其对可照时数的影响,利用ArcGIS的空间分析功能,将坡度按每5°分类,大于75°作为一类,共分16类统计不同坡度等级处不同空间分辨率的1月和7月可照时数,结果见表4和表5。
由表4可看出,基于4种分辨率DEM计算的1月可照时数随坡度变化表现出共同特征,即在一定坡度范围(0−55°),坡度越陡,可照时数越少,与10m分辨率下可照时数的差值随着分辨率的降低而增加;各分辨率的差别在于:分辨率越低,坡度的空间异质性越差,甚至900m分辨率下的模拟结果不存在坡度大于25°的区域,在>55°的陡坡区域,坡度可能不是主要影响因素,因此,导致可照时数随坡度先增加后减少的变化特征。由表4还可见,30m、90m和900m分辨率下模拟的可照时数在不同坡度上与10m分辨率下的差值表现为,在<5°的平缓坡区域差值最小,>5°区域不同分辨率下的差值呈现不同的变化规律,30m分辨率下的差值在5°−25°区域呈现减少趋势,而在25°−70°区域呈现增加趋势,90m分辨率下的差值在5°−25°区域无明显变化规律,而在25°−60°区域也呈现增加趋势,900m分辨率下的差值在5°−20°区域也呈现增加趋势,30m、90m和900m分辨率下最大差值分别达到66、56、52h左右,相当于每日平均多算2.1、1.8和1.7h。
由表5可以看出,7月可照时数随坡度的总体变化与1月相比具有共同特点,即坡度越陡,可照时数越少,与10m分辨率下可照时数的差值也随着分辨率的降低而增加,900m分辨率下计算结果也不存在坡度大于25°的区域。无论哪种分辨率下,与10m分辨率下可照时数的差值均在<5°的平缓坡区域最小。各分辨率的差别在于,无论哪个坡度等级,30m、90m和900m分辨率下7月可照时数与10m分辨率下的差值均小于1月,尤以30m和90m分辨率下的差值在>40°的较陡区域减小较多,且在>5°区域两个分辨率下的差值表现不同,30m分辨率下的差值在海拔5°−25°区域呈现减少趋势,而在25°−45°区域呈现增加趋势,>45°区域的波动较大,无明显变化规律,90m分辨率下的差值在5°−25°区域也呈现减少趋势,在25°−40°区域呈现增加趋势,>40°区域无明显变化规律,而900m分辨率下与10m分辨率下可照时数的差值,在不同海拔区域变化趋势不明显。30m、90m和900m分辨率下可照时数与10m分辨率下的最大差值分别为10、19、36h左右,相当于日均多算了0.3、0.6和1.2h。

表4 分坡度统计不同空间分辨率下的1月可照时数(h)
注:− 表示无统计值。下同。
Note: − means no statistical value. The same as below.
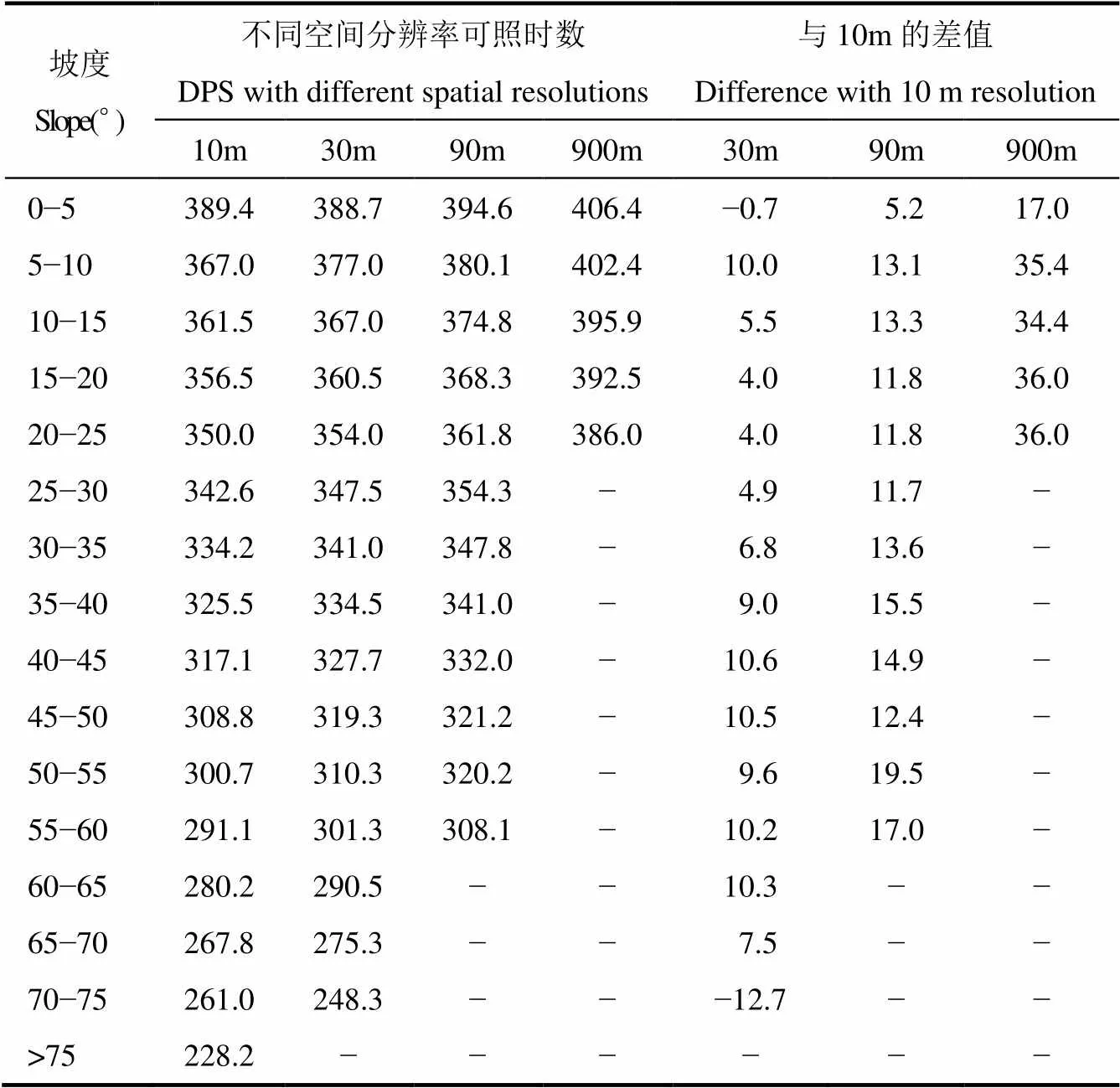
表5 分坡度统计不同空间分辨率下的7月可照时数
2.4 DEM尺度对典型月可照时数随坡向分布的影响
利用ArcGIS的空间分析功能,将坡向划分为8个方位,分别统计各方位1月和7月可照时数的平均值(图4),定量分析DEM尺度对1月和7月可照时数随坡向分布的影响。
由图4可见,基于4种分辨率DEM计算的1月和7月可照时数随坡向变化均表现出共同特点,即东南−西南坡、东坡−西坡以及东北−西北坡之间的差异均较小,南坡−北坡之间的差异均较大;随着分辨率的减小,任何坡向的可照时数均呈现增多趋势,其中,1月在东坡−西坡的增幅与7月基本相同,900m分辨率的可照时数在不同坡向的差异均很小,其不同特征表现为,30m、90m和900m分辨率下1月可照时数与10m分辨率下在偏北坡(包括西北坡、北坡和东北坡)的差值大于7月,其中最大差值在1月北坡上,分别达到42、79、149h左右,相当于1月每日平均多算了1.4、2.5和4.8h,而在偏南坡(包括西南坡、南坡和东南坡)的差值小于7月,其中最大差值在7月南坡或西南坡上,分别达到16、29、66h左右,相当于7月每日平均多算0.5、0.9和2.1h。无论哪种分辨率,对于1月可照时数,南坡最多,其余方位表现为东南坡/西南坡>东坡/西坡>东北坡/西北坡,北坡最小;而对于7月可照时数,北坡最多,其余表现为东北坡/西北坡>东坡/西坡>东南坡/西南坡,南坡最小。可见,分辨率对1月和7月可照时数的计算结果均有明显影响,分辨率越低,计算的可照时数越多,1月每日可照时数可能偏多1.4~4.8h,而7月每日可照时数可能偏多0.5~2.1h。
3 结论与讨论
(1)DEM存在空间尺度效应,因此,基于DEM的可照时数模拟也必然受到DEM空间尺度效应的影响,1月或7月模拟结果的空间异质性均随分辨率的减小而减小,900m分辨率下的结果随地形的变化特征不明显,其它分辨率的7月模拟结果受地形影响比相应分辨率下1月的模拟结果更明显。
(2)随着分辨率的减小,1月或7月模拟结果的平均值均逐渐增加,且1月的增幅大于7月。由于模拟结果的最大值分布在平地或山顶,对分辨率不敏感,因此,不同分辨率下模拟的最大可照时数基本无差异,而最小值分布在坡度和地形遮蔽度大的区域,对分辨率较敏感,随分辨率变化较大。由于随分辨率的减小,模拟结果精度降低,空间异质性变小,因此标准差减小。
(3)可照时数受海拔高度影响明显,平地和山脊处最多,海拔200−400m区域受地形遮蔽影响大,可照时数最少,400−1100m区域随海拔高度增加逐渐增加。以10m分辨率模拟结果为参照,30m、90m和900m分辨率下的差值均随分辨率的减小而增加。在海拔<100m的平地区域差值较小,>100m区域随海拔增加呈现增加趋势,700−900m区域差值最大,1月日平均约多算0.7、1.4和2.9h,相对1月,分辨率对7月模拟结果影响稍弱,7月日均约多算0.5、0.9和2.3h。

图4 不同分辨率下1月和7月可照时数随坡向的变化(h)
(4)可照时数受坡度影响也十分明显。在0−55°坡度范围,坡度越陡,可照时数越少,与10m分辨率的差值随分辨率的降低而增加,且30m、90m和900m分辨率下的最小差值均在<5°的平缓坡区域,最大差值出现在不同坡度等级,1月日均多算2.1、1.8和1.7h,7月日均多算0.3、0.6和1.2h。
(5)受太阳高度角的影响,坡向对可照时数的影响也不容忽视。南坡−北坡之间的差异较大,东南−西南坡、东坡−西坡以及东北−西北坡之间的差异较小;总体分布特征表现为,1月,南坡>东南坡/西南坡>东坡/西坡>东北坡/西北坡>北坡,7月,北坡>东北坡/西北坡>东坡/西坡坡>东南坡/西南坡>南坡;不同坡向上,30m、90m和900m分辨率下可照时数与10m分辨率下的差值随分辨率的降低而增加,在偏北坡(包括西北坡、北坡和东北坡)上,1月差值大于7月,最大差值出现在1月的北坡上,日均多算1.4、2.5和4.8h,而在偏南坡(包括西南坡、南坡和东南坡)上,1月的差值小于7月,最大差值出现在7月的南坡或西南坡上,日均多算0.5、0.9和2.1h。东坡−西坡上,1月与7月的变化基本一致。
山区的光温水等主要气候要素受局地地形影响呈现显著的空间异质性,目前,高精度DEM、数字地形分析、基于遥感反演的地表参数获取等综合应用可显著提高山区气候要素空间分布的模拟精度,能够在一定程度上解决由于山区气象站点稀少估算气候要素空间分布困难等现实问题,然而,山区气候复杂多变,如何准确定量分析山区气候要素和诸多地形因子之间的关系并提高空间分布的模拟精度一直是研究热点和难点,还需深入研究。
[1] 翁笃鸣,罗哲贤.山区地形气候[M].北京:气象出版社,1990.
Weng D M,Luo Z X.Topographical climate in mountainous areas[M].Beijing:China Meteorological Press,1990.(in Chinese)
[2] 李占清,翁笃鸣.一个计算山地可照时间的计算机模式[J].科学通报,1987,(17):1333-1335.
Li Z Q,Weng D M.A computer model to determine topographic parameters[J].Acta Geographica Sinica,1987,(17): 1333-1335.(in Chinese)
[3] 傅抱璞.山地气候[M].北京:科学出版社,1983.
Fu B P. Climate in mountainous areas[M].Beijing:Science Press,1983.(in Chinese)
[4] 傅抱璞,虞静明,卢其尧.山地气候资源与开发利用[M].南京:南京大学出版社,1996.
Fu B P,Yu J M,Lu Q Y.Climate sources,development and utilization in mountainous areas[M].Nanjing:Nanjing University Press,1996.(in Chinese)
[5] 朱志辉.等可照时间与等日照方位[J].中国科学(B辑),l987, (12):1340-1347.
Zhu Z H.Equal insolation duration and equal sunshine azimuth[J].Science in China Series B,l987,(12):1340-1347.(in Chinese)
[6] Dozier J,Outcalt S I.An approach to energy balance simulation over rugged terrain[J].Geographic Analysis,1979, 11(1):65-85.
[7] Dubayah R,Dozier J,Davis W F.Topographic distribution of clear sky radiation over the Konza Prairie,Kansas[J].Water Resources Research,1990,26(4):679-690.
[8] Dozier J,Frew J.Rapid calculation of terrain parameters for radiation modeling from digital elevation data[J].IEEE Transaction on Geoscience and Remote Sensing,1990,28(5): 963-969.
[9] Kumar L,Skidmore A K,Knowles E.Modeling topographic variation in solar radiation in a GIS environment[J]. International Journal of Geographic Information Science,1997, 11(5):475-497.
[10] Pinde F U,Rich P M.A geometric solar radiation model with application in agriculture and forestry[J].Computer and Electionics in Agriculture,2002,37:25-35.
[11] 李新,程国栋,陈贤章,等.任意地形条件下太阳辐射模型的改进[J].科学通报,1999,44(9):993-998.
Li X,Cheng G D,Chen X Z,et al.Modification of solar radiation model over rugged terrain[J].Chinese Science Bulletin,1999,44(9):993-998.(in Chinese)
[12] 曾燕,邱新法,缪启龙,等.起伏地形下我国可照时间的空间分布[J].自然科学进展,2003,13(5):545-548.
Zeng Y,Qiu X F,Miao Q L,et al.Distribution of possible sunshine durations over rugged terrains of China[J]. Progress in Natural Science,2003,13(5):545-548.(in Chinese)
[13] 黄晚华,帅细强,汪扩军.考虑地形条件下山区日照和辐射的GIS模型研究[J].中国农业气象,2006,27(2):89-93.
Huang W H,Shuai X Q,Wang K J.A study on GIS-based model of sunlight and radiation in view of terrain in mountain areas[J].Chinese Journal of Agrometeorology, 2006,27(2): 89-93.(in Chinese)
[14] 李军,黄敬峰.基于DEM的山地可照时间的空间分布[J].浙江大学学报(理学版),2007,34(3):346-350.
Li J,Huang J F.Spatial distribution of duration of possible sunshine based on DEM in mountain area[J].Journal of Zhejiang University (Science Edition),2007,34(3):346-350. (in Chinese)
[15] 孙娴,王娟敏,姜创业,等.陕西省山地日照时间的空间分布特征[J].自然资源学报,2010,25(4):625-635.
Sun X,Wang J M,Jiang C Y,et al.The spatial distribution of sunshine duration of mountain terrain[J].Journal of Natural Resources,2010,25(4):625-635.(in Chinese)
[16] 王怀清,殷剑敏,占明锦,等.考虑地形遮蔽的日照时数精细化推算模型[J].中国农业气象,2011,32(2) :273-278.
Wang H Q,Ying J M,Zhan M J,et al.Refine project model of sunshine resources in China considering terrain masking[J]. Chinese Journal of Agrometeorology,2011,32(2):273-278.(in Chinese)
[17] 张超,吴良林,杨妮,等.基于GIS的喀斯特山区实照时数时空分布研究:以广西巴马瑶族自治县为例[J].自然资源学报,2014,29(11):1968-1978.
Zhang C,Wu L L,Yang N,et al.Study on temporal and spatial distribution of sunshine duration based on GIS in karst mountain area-taking Guangxi Bama county for example[J]. Journal of Natural Resources,2014,29(11):1968-1978.(in Chinese)
[18] 卢燕宇,田红,侯恩兵,等.实际地形下地表太阳总辐射的简化算法及应用[J].中国农业气象,2017,38(7): 397-406.
Lu Y Y,Tian H,Hou E B,et al.A simplified calculation method of surface solar radiation over rugged terrains:the procedure and its application in Anhui province[J].Chinese Journal of Agrometeorology,2017,38(7):397-406.(in Chinese)
[19] 汤国安,刘学军,闾国年.数字高程模型及地学分析的原理与方法[M].北京:科学出版社,2005.
Tang G A,Liu X J,Lv G N.Principles and methods of digital elevation model and analysis[M].Beijing:Science Press,2005. (in Chinese)
[20] Daniel W M,Brendan G M,Brian L Z.Calibration and sensitivity analysis of a spatially distributed solar radiation model[J].International Journal of Geographical Information Science,1999,13(1):49-65.
[21] 张勇,陈良富,柳钦火,等.日照时间的地形影响与空间尺度效应[J].遥感学报,2005,9(5):521-530.
Zhang Y,Chen L F,Liu Q H,et al.Topographic and spatial- scaling effects on the sunlit time of the different terrains[J]. Journal of Remote Sensing,2005,9(5):521-530.(in Chinese)
[22] 姜创业,孙娴,王娟敏,等.山地天文辐射的地形影响与空间尺度效应研究[J].高原气象,2010,29(5):1230-1237.
Jiang C Y,Sun X,Wang J M,et al.Influences of various local topographic factors on astronomical radiation of mountain and its spatial scale effect in mountainous region[J].Plateau Meteorology,2010,29(5):1230-1237.(in Chinese)
Effect of Spatial Scale of DEM on Spatial Simulation of Duration of Possible Sunshine: A Case Study in Xianju County, Zhejiang Province
LI Jun1,2,3,WANG Chao1,ZHAO Yu-zhu1
(1.College of Geography and Tourism, Chongqing Normal University, Chongqing 401331, China; 2.Key Laboratory of GIS Application of Chongqing, Chongqing 401331; 3.Chongqing Key Laboratory of Earth Surface Processes and Environmental RemoteSensing in Three Gorges Reservoir Area, Chongqing 401331)
To analyze the effects of DEM with different spatial resolution on the numerical simulation of Duration of Possible Sunshine (DPS) based on DEM, Xianju County in Zhejiang Province was selected as the study area. DEM data with four spatial resolutions (10m, 30m, 90m, and 900m) derived from 1:10000 digital topographic map, ASTER GDEM, SRTM and GTOPO30´, respectively were used in this study. The topographic factors of altitude, slope, aspect, etc were derived from DEM. Using digital terrain analysis and spatial analysis for topographic factors and the distributed statistical model of DPS in GIS platform, this paper simulated the spatial distribution of DPS with four spatial resolutions in January and July. Then the effect of DEM scale on DPS simulation was analyzed. The results showed that spatial heterogeneity of DPS decreased as the spatial resolution decreased. Spatial distribution characteristics of DPS with topographic factors became increasingly hard to identify. The spatial data statistics showed that the average value increased with decreasing spatial resolution, while the standard deviation decreased. The maximum value varied little with spatial resolution, but the minimum value was quite different. Affected by altitude and other topographical factors, DPS was longest on flat and mountain ridges, while it was shortest in the region distributed at altitudes from 200−400m above sea-level. Moreover, it increased with the increasing altitude from 400−1100m above sea-level. Taking the DPS with 10m resolution as reference, the difference between the DPS with the other three spatial resolutions and the DPS with 10m resolution increased with the decrease of resolution. The minimum was at an altitude of <100m. The greatest differences were concentrated in the region of 700−900m. The average daily DPS in January were about 0.7h, 1.4h, and 2.9h more, while the one in July were about 0.5h, 0.9h, and 2.3h more. The DPS decreased with the increase of slope when the slope was in the range of 0−55°. The difference between the DPS with three spatial resolutions (30m, 90m, and 900m) and the reference value with 10m resolution increased with the decrease of resolution. The minimum all appeared in the flat region of slope 0−5°. The maximum occurred in the area with a steeper slope. The average daily DPS in January were about 2.1h, 1.8h, and 1.7h more, while the one in July were about 0.3h, 0.6h, and 1.2h more. Due to the effect of sloar altitude and azimuth angle, there was a great DPS differences between the south slope and the north slope. While the differences between SE slope and SW slope, E slope and W slope, NE slope and NW slope were smaller. The DPS differences with the reference value in all slopes increased with the decrease of resolution. In the northern slope (N, NE, and NW slopes), the difference in January was greater than that in July. The maximum occurred in the northern (N slope) slope of January. The average daily DPS were about 1.4h, 2.5h, and 4.8h more. In the southern slope (S, SE, and SW slopes), the difference in January was less than that in July. The maximum occurred in the southern slope (S or SW slope) of July. The average daily DPS were about 0.5h, 0.9h, and 2.1h more.
Mountain area; Duration of possible sunshine; Digital elevation model; Scale effect; Spatial distribution
10.3969/j.issn.1000-6362.2019.04.006
2018−10−10
重庆市前沿与应用基础研究计划一般项目(cstc2015jcyjA0332);国家自然科学基金(41807498)
李军(1974−),博士,副研究员,主要从事农业遥感和地理信息系统应用研究。E-mail: junli@cqnu.edu.cn
李军,王超,赵玉竹.DEM空间尺度对可照时数模拟结果的影响:以浙江省仙居县为例[J].中国农业气象,2019,40(4):250-259
