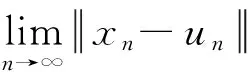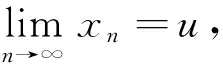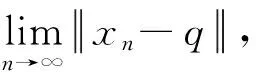渐进非扩张映射混合迭代序列的均衡问题和不动点问题
2016-03-15沈金良黄建华
沈金良, 黄建华
(1. 福州大学至诚学院, 福建 福州 350002; 2. 福州大学数学与计算机科学学院, 福建 福州 350116)
渐进非扩张映射混合迭代序列的均衡问题和不动点问题
沈金良1, 黄建华2
(1. 福州大学至诚学院, 福建 福州 350002; 2. 福州大学数学与计算机科学学院, 福建 福州 350116)
使用混合投影方法, 引入一种新的迭代算法, 在Hilbert空间中寻找均衡问题的解集和渐进非扩张映射的不动点集的公共点. 在一定条件下, 得出了弱收敛和强收敛定理.
均衡问题; 不动点问题; 混合迭代; 渐进非扩张映射; Hilbert空间
0 引言

(1)
把式(1)的解记为EP(G), 即EP(G)={x∈C:G(x,y)≥0, ∀y∈C}.

Wang[5]介绍了下列迭代序列: 给定x0∈H,
(2)
其中:Tλx=Tx-λμF(Tx), ∀x∈H,F:H→H是k-Lipschitzian和η-强单调映射. 并且在适当的条件下, 证明了式(2)所示的序列{xn}强收敛和弱收敛于T的不动点.
Ceng等[2]在Hilbert空间中引入了k-集伪压缩映射的迭代方法: 设T为k-集伪压缩映射,x1=x∈H, 则
(3)
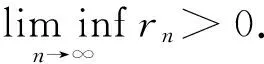
沈金良[3]研究了在Hilbert空间中的混合迭代序列, 即任意给定x0∈H, 则有
(4)
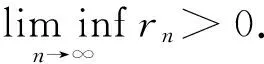
给定x1∈C,T:C→C是渐进非扩张映射,f:C→C是L-Lipschitzian映射. 假设{αn}是(0, 1)里的一个数列, {λn}⊂[0, 1). 定义渐进非扩张映射T的混合迭代方法如下:
(5)
主要目的是在Hilbert空间中研究式(5)所定义的渐进非扩张映射混合迭代序列的均衡问题和不动点问题, 并得到相应的弱收敛和强收敛定理. 所取得成果把文献[3]结论中的非扩张映射T推广到渐进非扩张映射, 还舍弃的映射f的η-强单调性这个条件.
1 预备知识


为了求解均衡问题EP(G), 假设G满足以下四个条件: 对所有的x,y,z∈C,
(A1)G(x,x)=0;
(A2)G是单调的, 即,G(x,y)+G(y,x)≤0(∀x,y∈C);
(A4)y|→G(x,y)是凸的和下半连续的.
为了证明本文的结论, 需要先介绍以下的引理.
引理1[6]设H是实的Hilbert空间, 则下列等式成立:


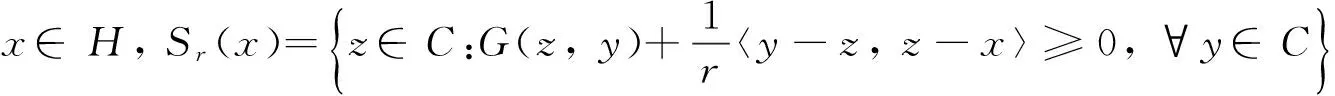
则有
1)Sr是单值的;
2)G(Sr)=EP(G);
3) EP(G)是非空闭凸的;


引理5[8]设E是一致凸Banach空间,b,c是两个常数, 满足0 引理6[9]设K是H的非空闭凸子集,T:H→H是渐进非扩张映射. 如果T有不动点, 那么I-T在0点是半闭的(这里I是H中的恒等映射). 定理1 设C是H中的非空闭凸子集,G:C×C→R是二元函数, 满足(A1)~(A4).T:C→C是渐进扩张映射,Ω=F(T)∩EP(G)非空,f:C→C是L-Lipschitzian映射. 任意给定x1∈C, {xn}和{un}如式(5)所示, 且满足以下条件: Ⅰ) 0 Ⅳ) {rn}⊂(0, ∞); Ⅴ)μ为正常数, 使得0<λnμ+kn<2. 那么, 3) {xn}和{un}都弱收敛于Ω中的点; 证明 1)任取q∈Ω, 由引理3中Sr的定义可知un=Srnxn, 因此 (6) 因为{kn}⊂[1, ∞),kn→1(n→∞), 所以kn是有界的. 故存在D≥1, 使得 (7) 假设vn=kn-1(n≥1), 则由条件Ⅱ)可得 (8) 因此 (9) (10) 假设 (11) 其中:d≥0是某个实数. 设σn=Tnun-λnμf(Tnun), 则有 (12) 由式(6), (7), (9)和(10)可得 因此, (13) 根据引理5和式(11)~(13)得 (14) 所以, (15) 任取q∈Ω, 由un=Srnxn可知 即有 (16) 由式(13)可知 (17) (18) 再结合式(17)有 (19) 根据定理1条件Ⅴ)和式(8)可得 0 由式(16), (19)有 (20) 移项整理, 根据条件Ⅰ)得 (21) 上式两边取n→∞可得 (22) 结合式(14)和式(22)有 (23) 所以, (24) (25) 由式(15), (24)可得 (26) 由式(22), (26)可得 (27) 假设u≠v. 因为H是Hilbert空间, 必然满足Opial条件. 所以 4) 任取q∈Ω, 由式(9), (10)得 (28) 对所有的p∈Ω, 上式取下确界得 定理2 在定理1的条件下, 如果T是弱紧的, 则{xn}和{un}强收敛于Ω中的点. [1]CENGLC,YAOCJ.Ahybriditerativeschemeformixedequilibriumproblemsandfixedpointproblems[J].JournalofComputationalandAppliedMathematics, 2008, 214(1): 186-201. [2]CENGLC,HOMIDANSA,ANSARIQH,etal. An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings[J]. Journal of Computational and Applied Mathematics, 2009, 223(2): 967-974. [3] 沈金良. 非扩张映射混合迭代序列的均衡问题和不动点问题[J]. 闽江学院学报, 2012, 33(5): 5-10. [4] COMBETTES P L, HIRSTOAGA S A. Equilibrium problem progamming in Hilbert spaces[J]. Journal of Nonlinear and Convex Analysis, 2005, 6(1): 117-136. [5] WANG L. An iteration method for nonexpansive mappings in Hilbert spaces[J]. Fixed Point Theory and Applications, 2007(1): 1-8. [6] MARINO G, XU H K. Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces[J]. J Math Anal Appl, 2007, 329: 336-346. [7] TAN K K, XU H K. Approximating fixed points of nonexpansive mappings by the Ishikawa iterations process[J]. Journal of Mathematical Analysis and Applications, 1993, 178: 301-308. [8] SCHU J. Weak and strong convergence to fixed points of asymptotically nonexpansive mappings[J]. Bulletin of the Australian Mathematical Society, 2013(4): 1-10. [9] CHO Y J, ZHOU H Y, GUO G. Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings[J]. Computers and Mathematics with Applications, 2004, 47(4/5): 707-717. (责任编辑: 林晓) Hybrid iteration method for equilibrium problems and fixed point problems of asymptotically nonexpansive mappings SHEN Jinliang1, HUANG Jianhua2 (1. Zhicheng College, Fuzhou University, Fuzhou, Fujian 350002, China;2. College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China) We introduce an new iterative scheme by using the hybrid projection methods for finding a common element of the set of solutions of an equilibrium problems and the set of fixed points of an asymptotically nonexpansive mapping in Hilbert spaces. Under some conditions, weakly and strongly convergence theorem are obtained in Hilbert spaces. equilibrium problems; fixed point problems; hybrid iteration; asymptotically nonexpansive mappings; Hilbert space 10.7631/issn.1000-2243.2016.05.0621 1000-2243(2016)05-0621-06 2016-01-14 沈金良(1982-), 讲师, 主要从事非线性分析研究, 181401539@qq.com 福建省自然科学基金资助项目(2014J01008); 福建省中青年教师教育科研资助项目(JA15624) O177.91 A2 主要结论