计入结构柔性和边界条件的内齿圈面内振动分析
2016-03-15卞世元刘先增
卞世元, 刘先增, 焦 阳, 张 俊, 4
(1. 安徽工业大学机械工程学院, 安徽 马鞍山 243032; 2. 天津大学机械工程学院, 天津 300072;3. 南京工艺装备制造有限公司, 江苏 南京 211178; 4. 福州大学机械工程及自动化学院, 福建 福州 350116)
计入结构柔性和边界条件的内齿圈面内振动分析
卞世元1, 刘先增2, 焦 阳3, 张 俊1, 4
(1. 安徽工业大学机械工程学院, 安徽 马鞍山 243032; 2. 天津大学机械工程学院, 天津 300072;3. 南京工艺装备制造有限公司, 江苏 南京 211178; 4. 福州大学机械工程及自动化学院, 福建 福州 350116)
采用弹性力学方法推导内齿圈的运动微分方程, 用摄动法求解无约束条件下内齿圈的固有频率和振型函数, 并通过消除永年项获得了含约束条件下的内齿圈面内振动频率的解析表达式. 以某汽车变速箱中的内齿圈为例, 运用所获的解析式计算了该齿圈的面内振动频率, 其结果与前人研究中的有限元仿真及模态实测数据吻合较好. 表明所提理论模型具有较高的计算精度, 能准确揭示内齿圈的振动特性. 最后, 依托所建理论模型, 分析内齿圈结构柔性和内、 外约束条件对其面内振动特性的影响. 计算结果表明, 内齿圈面内振动频率随外约束刚度的增大而增大, 且当内齿圈所有外约束的刚度之和不变时, 降低单个外约束的刚度也即增大外约束的数目可小幅度地降低齿圈的面内振动频率; 相比于外约束, 内约束数目和刚度对内齿圈面内振动频率影响较小, 随着内约束数目和刚度的增加, 同一节径数下的内齿圈面内振动频率呈缓慢增大趋势. 啮合相位变化时, 面内振动模式的固有频率变化较大.
行星齿轮; 内齿圈; 结构柔性; 边界条件; 固有频率
0 引言
为提高行星轮系的功重比, 工程中常采用柔性内齿圈的设计方案. 此举不仅可有效减轻轮系质量, 还可借助内齿圈的柔性来提升轮系的均载性能[1]. 作为系统振动能量传递的主要路线和关键节点, 轮系各构件间的动态载荷往往经由内齿圈传至机体, 故内齿圈的柔性及由此激起的谐振可能会加剧系统的振动, 而轮系的振动和噪声又是影响系统可靠性、 寿命及操作环境的关键因素. 已有研究表明, 对于薄缘内齿圈或具有浮动行星轮的系统, 内齿圈的柔性对系统动态特性影响显著[2]. 因此, 从抑制系统振动、 降低传动噪声的角度考虑, 在行星轮系的动态分析及设计中必须计入内齿圈振动特性的影响. 围绕行星轮系的动力学问题, 学术界开展了大量研究, 内容涉及动力学建模、 固有特性分析、 动态响应求解、 振动噪声抑制等多个方面[3]. 这其中, 动力学建模和固有特性分析是进行后续动力性能研究及减振降噪的基础.
Kahraman等[4-6]运用有限元法相继建立了行星轮系的准静态和动态受力模型, 分析了内齿圈柔性对齿轮应力、 各行星轮间载荷分配以及系统动态特性的影响. 然而, 上述有限元模型虽计及内齿圈对系统受力特性的影响, 但其对内齿圈边界条件的处理过于简单, 仅将内齿圈轮缘表面全部节点按固定约束处理, 这与内齿圈的实际安装工况有一定出入. 由于有限元模型的分析精度取决于对边界条件的正确处理, 因此, 上述简化必然会降低系统动态特性预测的准确性. Tanna等[7-8]从柔性内齿圈自身振动特性出发, 建立了用于预测该构件自由振动特性的有限元模型, 得出了内齿圈自由振动下的4种典型振动模式, 并进一步探讨了不同约束方式及结构简化对内齿圈固有特性的影响. 此后, 他们又进一步分析了设计参数对内齿圈自由振动特性的影响规律[9]. 但是, Tanna等人的研究并未考虑轮系中行星轮对内齿圈的约束, 也未计及机体对内齿圈外轮缘的周向约束, 而仅对内齿圈外轮缘作简单的径向约束处理. 显然, 上述约束处理与内齿圈的真实边界条件相差甚远, 其相关结论也不宜直接应用于轮系的动态分析和设计.
Kim等[10]研究了恒转速薄圆环的非线性自由振动. Metrikine和Forbes等[11-12]对旋转移动载荷作用下的光滑弹性圆环进行了振动分析. Wu和Cooley等[13-14]将内齿圈处理为在一定约束作用下的光滑弹性圆环, 并对其进行了振动分析. 在此基础上, Parker等[15]进一步探讨了移动变刚度弹簧约束下光滑圆环的振动稳定性问题. 此后, Parker又将该模型延伸至行星轮系的动力学研究, 相继建立了计入支承约束的柔性内齿圈的振动模型以及包含柔性内齿圈的行星轮系动力学模型, 并分别对内齿圈和行星轮系的振动特性进行了探讨[16-18]. 上述研究中, 文[13]将内齿圈的边界条件视为两组动态激励, 并采用一组连续分布且正交的内外弹簧约束来模拟其边界条件. 然而, 由于内齿圈内外约束的数目即行星轮个数与外轮缘上花键齿的数目一般并不相同, 故该文将内外约束表征为若干正交弹簧且认为内外约束刚度相同的做法与实际不相符. 并且, 上述研究也未就内外约束的数目及约束强度对内齿圈振动特性的影响作进一步探讨.
本研究从实际设计角度出发, 明确不同构型方案(如行星轮个数)下内齿圈的安装结构(如轮缘厚度、 花键齿的个数及尺寸)对内齿圈乃至轮系振动特性的影响, 对设计具有优良动态性能的行星传动装置具有重要的工程意义. 为实现这一目标, 在结构设计阶段采用有限元法无疑是时间成本较高的一种措施; 相反, 若能借助解析模型揭示出相关设计参数对内齿圈振动特性的影响规律, 并初步给出主要设计参数的选择区间, 则可大大减少结构参数优选的工作量. 基于这一考量, 拟采用弹性力学方法建立综合考虑行星轮啮合约束和花键套支承约束的柔性内齿圈的动力学模型, 通过对内齿圈结构柔性和边界条件的量化处理, 揭示内齿圈结构参数、 内外约束的数目和强度对其振动特性的影响规律, 希冀为后续的行星轮系动态设计和性能优化提供初步的力学计算依据.
1 动力学模型
为降低建模和数学处理难度, 将行星内齿圈简化为如图1所示的具有等效内外半径并同时受内外约束的光滑弹性圆环(薄壁圆环理论). 由有限元模态分析并经数据回归知, 当光滑弹性圆环的内、 外径分别取为行星内齿圈的分度圆和外缘半径时, 其自由振动特性与真实内齿圈的振动特性非常贴近. 有鉴于此, 后续建模和分析中将上述光滑弹性圆环的内、 外径分别设为行星内齿圈的分度圆半径rr和轮缘外径ro, 并设定弹性圆环的中性层半径为r.
对直齿行星传动而言, 内齿圈一般仅作平面振动, 故假设圆环截面在变形过程中仍保持平面(见图1), 且始终与其自身轴线相垂直, 仅考察圆环的平面内振动. 由弹性力学理论可知, 上述圆环的变形状态可由中性层轴线上各点沿r、θ方向的切向位移分量u和径向位移分量w所确定, 其中:u、w均为θ和t的函数, 并可写为u(θ,t)和w(θ,t). 为清晰计, 后续如不做特别说明,u(θ,t)和w(θ,t)一律简写为u和w.
由行星轮系的运行工况知, 行星内齿圈同时受行星轮啮合力和机体支承力的约束. 不妨将内齿圈与行星轮间的啮合力视为内约束, 而将内齿圈与机体间的支承力视为外约束. 其中: 内约束以一组沿内啮合副理论啮合线方向并与综合平均啮合刚度等效的线性弹簧表征, 其与径向线之间的夹角设为γ, 弹簧数目由啮合副数目决定; 外约束以一组分布于圆环外缘且与实际支承刚度等同的正交线性弹簧表征, 其方向分别取为圆环上约束点的切向和径向, 其正交弹簧组的数目由内齿圈的实际安装结构确定. 显然, 经上述定义的内、 外约束刚度均为约束位置的函数. 不失一般性, 分别以d(θ)、l(θ)表征内外约束刚度的分布特性, 而以kp、kh表征内、 外约束的强度, 则内、 外约束刚度分别为kpd(θ)和khl(θ). 其中:kp、kh又可进一步分解为沿切向和径向的kpu、kpw和khu、khw. 清晰起见, 图中仅示出外约束刚度的分解示意.
针对图1所示的行星内齿圈等效力学模型, 可取该光滑弹性圆环的任一微元段进行研究. 图2列出了弹性圆环任一微元段的受力状况[2,19].
图中:Fu、Fw分别为内齿圈微元段所受的切向力和径向力. 由图2并结合弹性力学相关理论, 可导出行星内齿圈沿切向和径向的运动微分方程为:
(1)
(2)
因设定行星内齿圈仅作平面振动, 故由弹性力学理论可知存在:
(3)
联立式(1)~(3)可得行星内齿圈的运动微分方程:
(4)
式中:M、L为微分算子, 且有:
(5)
不妨令:khu=δ1kh,khw=δ2kh,kp=δ3kh, 则有:
(6)

(7)
式中:L1为算子, 且有:
(8)
其中:g、h均为位置θ的函数, 且有:
(9)
2 振动特性分析
针对式(7)表征的行星内齿圈运动微分方程, 可采用摄动法求解其无约束条件下的固有频率及振型函数.
不妨设定行星内齿圈的振型函数为u*(θ,t)=u*(θ)ei ω t, 为方便表述, 省略上标“*”, 将其简写为u(θ,t)=u(θ)ei ω t并代入式(7), 可得内齿圈的特征值方程:
(10)
由摄动法, 可将u、ω2展开为ε的幂级数:
(11)
将式(11)代入式(10)并省略高阶项, 可得:
(12)
(13)
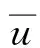
(14)
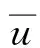
(15)
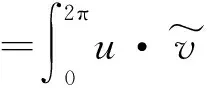
(16)
式中:δkj为克罗内克函数, 其数学表述为:
(17)
将式(14)代入式(16), 并化简可得:
(18)
(19)
由ε1, 即式(13)的可解性条件, 可写出:
(20)
考虑到ein θ可按欧拉公式展开为三角函数的组合, 且三角函数在区间[0, 2π]上存在积分正交性, 同时注意到g、h均为θ的函数, 故可将g(θ)、h(θ)函数展开为傅里叶级数形式, 从而与ein θ形式统一.g(θ)、h(θ)的傅里叶级数展开形式为:
(21)
式中:gm、hm为g(θ)、h(θ)的傅里叶系数.
由式(9)可知,g、h为d(θ)、l(θ)的函数, 故采用同样方法进一步将d(θ)、l(θ)展开为:
(22)
式中:dm、em为d(θ)、l(θ)的傅里叶系数, 且有:
(23)
将式(21)~(23)代入式(20), 化简并组装后可得:
(24)
式中:D为厄米特算子;I为单位矩阵;λn为特征值;an为对应的特征向量, 且有:
(25)
式(24)的特征值问题为:
(26)
求解式(26)可得方程(24)的特征值:
(27)
式中:i=1, 2, 且当i=1时“±”取“+”,i=2时, “±”取“-”.
将式(27)代入式(24)后, 可进一步求出特征向量an, 进而得到an, 1以及an, 2的值, 最后通过式(15)可确定u0.
式(27)表明,λni中包含g、h的傅里叶展开系数项, 进一步由式(23)可知,λni为内、 外约束刚度分布d、l的函数. 以下将推导λni与内、 外约束刚度分布特性之间的函数关系.
不失一般性, 对行星内齿圈的相关参数作如下设定:
1) 内齿圈模数为m, 齿数为z, 齿根圆半径为rf, 轮缘外径为ro, 齿宽为b0;
2) 内齿圈与np个周向均布的行星轮相啮合, 其综合平均啮合刚度为kp, 各啮合副的重合度为εrp;
3) 内齿圈通过nh个均布的机械连接(花键、 销钉等)与机体相连, 各连接处刚度设为kh, 且其对应的圆心角设为εh.
经上述设定后, 行星内齿圈的内、 外约束刚度分布特性d(θ)、l(θ)可表示为:
(28)
将d(θ)、l(θ)在θ的负半轴上作偶延拓, 可将式(28)按傅里叶级数展开, 可得:
(29)
写成复数形式为:
(30)
由上式可得:
(31)
将式(31)代入式(23), 并联立式(27), 可得:
(32)
上式中, 系数C1、C2为:
(33)
其中:C3=sin(2npnδp),C4=sin(2nhnδh).
将式(32)代入式(24), 可得特征向量:
(34)
再由振型归一化条件〈Mu0,u0〉=1, 可得:
(35)
进而可得无约束下内齿圈振动位移函数为:
(36)
式(32)、 (36)分别给出了无约束情况下行星内齿圈的振动频率和位移函数. 为考虑内、 外约束对振动特性的影响, 还应在上述两式基础上, 进一步计入ε1式中的频率修正项. 因此, 将式(36)代入式(13), 可得:
(37)
代入各算子, 可得式(37)右端两项为:
(38)
(39)
式中:C6=δ1+n2δ2,C7=δ3cosγ+n2δ3sinγ.
经过量纲还原可得计入内、 外约束边界的行星内齿圈的面内振动频率为:
(40)
式中:ρ为内齿圈的线密度;r为内齿圈中性层半径;E为弹性模量;Jz为等效圆环截面绕其自身轴线的转动惯量;ν为泊松比.
3 算例分析与模型验证
为方便比较, 不妨以文[20]中的某汽车变速箱中内齿圈为例, 结构参数如下:z=78, 模数m=1.55 mm, 内径da=121.00 mm, 外径ro=135.56 mm, 行星轮个数np=4, 花键齿数h=15, 外轮缘键角宽t=6°, 齿宽b0=30.73 mm, 内刚度kp=60 MN·m-1, 外刚度kh=20 MN·m-1. 采用基于上述弹性力学模型推导的计入内、 外约束的内齿圈面内振动方程分析其振动特性.
由上述参数可进一步计算出频率修正项b1, 将其代入式(40)即得内齿圈面内振动频率. 考虑到低频特性对轮系振动特性的影响较大, 仅给出内齿圈前6阶面内振动的结果, 即节径数为2到7的面内弯曲振动固有频率, 如表1所示. 为清晰计, 表1进一步给出了文献[20]中的有限元模态分析结果和模态试验结果.
由表1可见, 上述理论计算频率与模态试验和有限元结果相比较, 误差约0~6%. 验证了该理论模型的合理以及适用性, 从而可用于后续的参数影响分析. 误差主要来源于有限元模型和理论模型的齿廓、 材料特性和边界条件等与真实齿轮之间存在微小的差别.

表1 面内弯曲固有频率Tab.1 The natural frequencies of the in-plane bending
4 参数影响分析
以表1参数为基准值, 运用本文所建理论模型, 考察内齿圈结构柔性及边界条件对内齿圈面内振动的影响.
首先分析齿圈结构柔性对面内振动的影响. 为直观计, 不妨以内齿圈轮缘厚度来表征齿圈的结构柔性. 篇幅所限, 仅给出轮缘厚度δ在[4, 7.2] mm变化时, 齿圈1、 2阶面内弯曲振动频率的变化, 其结果如图3所示.
由图3可见, 在其他参数不变时, 随着内齿圈轮缘厚度的增大, 同一节径下的面内弯曲振动频率显著增大. 换言之, 内齿圈的结构柔性可有效降低其面内弯曲振动频率.
接下来考察外约束刚度对内齿圈面内振动的影响. 图4所示为内齿圈与机体间的单个外约束刚度kh在[107, 108]N·m-1间变化时第1、 2阶面内弯曲振动频率的变化.
图4表明, 随着外约束刚度的增大, 同一节径数下的内齿圈面内振动频率呈缓慢的单调递增趋势. 对比图3、 4可知, 内齿圈面内振动频率受其轮缘厚度(结构柔性)的影响更加明显, 而受外约束刚度的影响程度则相对较弱. 因此可以推断, 在行星轮结构设计中, 可在保证内齿圈与机体间的约束强度前提下适当增大轮缘厚度以提高内齿圈面内振动频率.
再来考察外约束总刚度不变时约束数目的影响. 不防定义外约束总刚度为Kh, 且Kh=nh×kh, 则计算可得上述算例中Kh=0.3 GN·m-1. 当Kh不变时, 外约束数目nh对内齿圈面内振动特性的影响如图5所示.
由图5可见, 当内齿圈所有外约束刚度之和Kh不变时, 外约束数目的增多将导致面内振动频率的缓慢降低, 且降低的速度随着外约束数目的增大而放缓.
最后分析内约束数目和内约束刚度对内齿圈面内振动的影响. 仍以n=2、n=3为例, 其面内振动频率的变化规律如图6、 7所示.
从图6可知, 其他条件不变时, 随着内约束数目的增多, 内齿圈的面内振动频率呈缓慢增大趋势, 但增幅很小. 相应地, 图7亦表明内约束刚度对内齿圈面内振动频率也有轻微影响, 随着内约束刚度的增大, 齿圈振动频率呈单调递增趋势. 将图6、 7与图4、 5对比可以发现, 相比于内约束, 外约束的数目和刚度对内齿圈面内振动的影响更为明显, 且内约束的数目和强度主要取决于行星轮布局和轮系基本参数设计, 因此在进行该类传动系统的动态设计和分析时, 应着重关注内齿圈的安装方式及其对轮系振动的影响.
6 结语
1) 将真实内齿圈结构简化为光滑弹性圆环、 将行星轮啮合约束和内齿圈安装约束处理为弹簧约束进而采用弹性力学方法建立内齿圈面内振动方程的思路是可行的, 基于所提理论模型的解析计算结果与有限元和实验数据吻合较好, 可准确揭示内齿圈的面内振动特性.
2) 有别于传统的有限元方法, 将内齿圈内外约束的具体结构表征为具有相应力学性能的弹簧约束的边界条件处理方案, 可极大提升建模和分析的效率. 此外, 可通过对外约束弹簧两正交方向上刚度的调整来模拟不同的齿圈安装方式(如花键、 销钉、 法兰或过盈), 从而极大地提升了模型的适应性, 为后续计入内齿圈柔性的行星轮系动力学分析提供了一种新的解决方案.
3) 内齿圈面内振动频率受其结构柔性的影响显著, 随着结构柔性的增加, 各阶面内振动频率呈明显单调递增趋势.
4) 内齿圈的外约束刚度和数目对其面内振动具有一定的影响, 约束刚度的增大将导致内齿圈面内振动频率的增高, 而外约束总刚度不变时约束数目的增多将使得内齿圈面内振动频率呈缓慢降低趋势. 因此, 在内齿圈的安装方式选择和动态设计时应考虑这一特性.
5) 相较于外约束, 内约束对内齿圈面内振动的影响较弱, 随着内约束数目和刚度的增大, 内齿圈各阶面内振动频率缓慢增大, 但增幅较小.
6) 内、 外约束的数目、 刚度及内约束位置均对内齿圈的振动特性产生影响. 相对而言, 内齿圈面内弯曲振型较刚体运动振型和面外弯曲振型更易受到边界条件(安装工况)的影响.
7) 面外弯曲和摆动模式受内约束位置的影响较小, 而面内弯曲模式受内约束位置的影响最大.
[1] BIBEL G D, REDDY S K, SAVAGE M,etal. Effects of rim thickness on spur gear bending stress[J]. Journal of Mechanical Design, 1994, 116(4): 1 157- 1 162.
[2] 张俊, 刘先增, 焦阳, 等. 基于刚柔耦合模型的行星传动固有特性分析[J]. 机械工程学报, 2014, 50(15): 104-112.
[3] COOLEY C G, PARKER R G. A review of planetary and epicyclic gear dynamics and vibrations research[J]. Applied Mechanics Reviews, 2014, 66(4): 040 804.
[4] KAHRAMAN A, VIJAYAKAR S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set[J]. Journal of Mechanical Design, 2001, 123(3): 408-415.
[5] KAHRAMAN A, KHARAZI A A, UMRANI M. A deformable body dynamic analysis of planetary gears with thin rims[J]. Journal of Sound and Vibration, 2003, 262(3): 752-768.
[6] KAHRAMAN A, LIGATA H, SINGH A. Influence of ring gear rim thickness on planetary gear set behavior[J]. Journal of Mechanical Design, 2010, 132(2): 021 002.
[7] TANNA R P, LIM T C. Effects of boundary conditions on the natural modes of transmission ring gear structure[C]//SAE Noise & Vibration Conference & Exposition. Michigan: SAE Technical Paper, 2001: 2001-01-1 416.
[8] TANNA R P, LIM T C. Modal frequency deviations in estimating ring gear modes using smooth ring solutions[J]. Journal of Sound and Vibration, 2004, 269(3): 1 099-1 110.
[9] TANNA R P, LIM T C. Parametric analysis of ring gear structure vibration modes[J]. International Journal of Acoustics and Vibration, 2006, 11(2): 93-105.
[10] KIM W, CHUNG J. Free non-linear vibration of a rotating thin ring with the in-plane and out-of-plane motions[J]. Journal of Sound and Vibration, 2002, 258 (1): 167-178.
[11] METRIKINE A V, TOCHILIN M V. Steady-state vibrations of an elastic ring under a moving load[J]. Journal of Sound and Vibration, 2000, 232(3): 511-524.
[12] FORBES G L, RANDALL R B. Resonance phenomena of an elastic ring under a moving load[J]. Journal of Sound and Vibration, 2008, 318(4): 991-1 004.
[13] WU X, PARKER R G. Vibration of rings on a general elastic foundation[J]. Journal of Sound and Vibration, 2006, 295(1): 194-213.
[14] COOLEY C G, PARKER R G. Vibration of high-speed rotating rings coupled to space-fixed stiffnesses[J]. Journal of Sound and Vibration, 2014, 333(12): 2 631-2 648.
[15] CANCHI S V, PARKER R G. Parametric instability of a rotating circular ring with moving, time-varying springs[J]. Journal of Vibration and Acoustics, 2006, 128 (2): 231-243.
[16] WU X, PARKER R G. Modal properties of planetary gears with an elastic continuum ring gear[J]. Journal of Applied Mechanics, 2008, 75(3): 031 014.
[17] PARKER R G, WU X. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear[J]. Journal of Sound and Vibration, 2010, 329(11): 2 265-2 275.
[18] PARKER R G, WU X. Parametric instability of planetary gears having elastic continuum ring gears[J]. Journal of Vibration and Acoustics, 2012, 134(4): 041 011.
[19] 焦阳. 含柔性齿圈的行星轮系动力学分析[D]. 马鞍山: 安徽工业大学, 2014.
[20] TANNA R P. Dynamic characteristics of ring-form structures with emphasis on automotive transmission ring gear vibrations[D]. Tuscaloosa: University of Alabama, 2002.
(责任编辑: 沈芸)
In-plane vibration analysis of ring gear with considerations for structural flexibility and boundary conditions
BIAN Shiyuan1, LIU Xianzeng2, JIAO Yang3, ZHANG Jun1, 4
(1. College of Mechanical Engineering, Anhui University of Technology, Ma’anshan, Anhui 243032, China;2. School of Mechanical Engineering, Tianjing University, Tianjing 300072, China;3. Nanjing Technical Equipment Manufacture Co LTD, Nanjing, Jiangsu 211178, China;4. College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China)
The differential equation of motion for the ring gear is derived and solved, leading to an analytical expression for the natural frequency of in-plane vibration. The proposed model is then applied to a ring gear in an automobile transmission gearbox to formulate the in-plane vibration characteristics and validated by numerical and experimental results in previous research, indicating the present model can be applied for further parameter studies. The effects of structural flexibilities as well as boundary conditions on in-plane vibration properties are investigated with the purpose of providing some useful information for planetary gear train designers. The studies show that the rim thickness affects the vibration frequencies significantly and the external constrains have a ‘stronger’ influence on the vibration frequencies than the internal constrains. It is suggested that more attentions should be made on the installing of ring gear to achieve good dynamic performance.
planetary gears; ring gear; structural flexibility; boundary conditions; natural frequency
10.7631/issn.1000-2243.2016.05.0694
1000-2243(2016)05-0694-09
2016-01-11
张俊(1981-), 教授, 主要从事机械传动、 机械系统动力学和机器人机构学研究, zhang_jun@tju.edu.cn
国家自然科学基金资助项目(50905122, 51375013); 安徽省自然科学基金资助项目(1208085ME64); 安徽工业大学研究生创新基金资助项目(2014055)
TH132.4
A
