基于极化特征的抗箔条干扰方法研究

， ， ，

(海军航空工程学院电子信息工程系， 山东烟台 264001)

0 引言

箔条由于使用方便、造价低廉，经过第二次世界大战以来大半个世纪的发展，已经成为使用最广泛的雷达无源干扰之一[1]。箔条主要用来干扰制导雷达，影响制导雷达开机后的搜索、捕捉和跟踪过程，避免防御方遭遇制导武器的攻击。箔条可以掩护飞机编队突防，也可以保护舰艇免受导弹打击。近代战争中的多次成功使用，证明箔条干扰在欺骗雷达、降低雷达目标识别能力方面取得了显著的效果。因此，世界各国的作战舰艇几乎都装备了箔条干扰设备。围绕箔条展开的干扰与抗干扰研究显得格外重要，研究箔条云回波信号特征将对雷达识别目标能力的提高提供有力的理论支持。

将目标的极化信息应用于雷达的目标识别，一直是雷达对抗与雷达极化学研究的热点，但是目标极化信息在雷达抗干扰方面的应用潜力还没有被充分挖掘出来。一方面，雷达组网抗干扰的措施应用不够广泛；另一方面，极化信息的研究没有达到与时域和频域相提并论的高度。通常对目标极化域信息的获取有两个途径：一是通过试验的方法，二是通过理论分析和仿真的方法。由于现有雷达体制的限制以及箔条外场测试的不便，通过试验手段获取箔条雷达回波信号的极化特性变得很困难。而且现有文献[2-5]对箔条极化域信息的研究主要集中于理论推导，不能完整体现其雷达回波信号的极化信息。针对以上问题，建立箔条云和常见目标(船、飞机)的模型，并利用电磁场数值计算方法计算得到不同目标的极化特性，为制导雷达实现基于极化特征的抗箔条干扰提供理论依据。

1 不同目标模型的建立

分析不同目标的极化特征，首先要建立合理的模型。对船和飞机等目标而言，参考目标的实际尺寸和形状，利用常见的绘图软件即可精确地绘制目标的实体模型。而对于箔条云模型而言，由于箔条在空中运动时，空气流动和箔条间相互碰撞等因素造成箔条之间运动状态相差很大，因此没有固定的模型可以准确描述箔条云的空间状态。文献[6-10]均对箔条云的运动扩散特性进行了研究。一般认为，箔条云在扩散过程中，形状逐渐由均匀球体变为扁长椭球体，并且箔条的位置在空间均匀分布或正态分布。对单根箔条而言，任意时刻箔条在空间的姿态随机，即箔条的俯仰角和方位角为0°～360°之间的任意值，以此为基础建立箔条云的空间分布模型。

1.1 箔条云模型的建立

当电磁波照射到箔条表面时会产生感应电流，感应电流在箔条周围产生的交变电磁场以波动的形式向外传播。由天线理论可知，长度为雷达信号波长一半的箔条具有最大的散射截面积，称为谐振散射箔条，缺点是该类箔条频带很窄。为克服该缺点，使箔条覆盖较宽的频带，具备同时干扰多个频段雷达的能力，一般将不同尺寸的箔条混合包装以满足要求。综合考虑箔条散射截面、频带宽度以及导电性能等因素，选择长度为半波长、长宽比为30、厚度忽略不计的理想金属导体作为箔条。

首先建立所需的不同尺寸单根箔条，然后根据空间分布的要求对单根箔条进行旋转、平移，即可得到箔条云模型。

对单根箔条而言，由于其厚度忽略不计，以矩形来近似，因此其空间位置可以由矩形的4个顶点唯一确定。若某根箔条的一个顶点在空间直角坐标系中的坐标为r0=(x0,y0,z0)，则随机产生的第i根箔条对应的顶点可以由r0依次绕x轴旋转αi角度、绕y轴旋转βi角度、绕z轴旋转γi角度，然后坐标平移(xi,yi,zi)得到。根据文献[11]的结论，这里αi,βi,γi均取[0,2π]的均匀分布随机数。旋转后的坐标(xsi,ysi,zsi)可以表示为

(1)

若箔条云在空间服从半径为R的球均匀分布，则平移坐标(xi,yi,zi)可以表示为

(2)

式中，r,θi,φi分别服从(0,R), (0,π), (0,2π)的均匀分布。

因此对应的变换后顶点坐标可以表示为

(x,y,z)=(xsi+xi,ysi+yi,zsi+zi)

(3)

同理可以得到第i根箔条的其他3个顶点坐标，从而确定第i根箔条的位置。由于箔条在空间分布时不会出现相互交叉的现象，需要判断第i根箔条与前i-1根箔条之间是否相互交叉，如果相交，则重新生成第i根箔条，反之，继续产生第i+1根箔条，直至产生所需数量的箔条云为止。将生成的箔条云模型进行剖分处理后就可以对箔条云的回波信号进行计算，分析其雷达回波特征。图1给出了半径为1 m、服从球体均匀分布的箔条云模型，并且箔条云由10 GHz和15 GHz对应的半波长、全波长箔条各1 000根组成。

固定矿浆pH为11.5±0.2，淀粉用量为100 mg/L，CaCl2用量为100 mg/L，两种捕收剂不同用量对三种矿物的浮选结果如图6所示。

1.2 船和飞机模型的建立

能够用于三维建模的软件有很多，3dsMAX具有功能强大、操作简单、软件之间兼容性好的特点，是现在应用最为广泛的三维模型制作软件，这里对船和飞机的建模由3dsMAX软件实现。

以船为例，首先构建船的主体：船身、操作台，然后制作船的附属部分：舵、桨、扶手等，最后将主体部分和附属部分进行组合变换，得到整体模型。具体操作流程不再赘述，图2和图3分别给出了救生艇和某型飞机的实体模型。

图2 救生艇实体模型

图3 某型飞机实体模型

其中，救生艇的长宽高分别为4.2 m×1.6 m×1.8 m；飞机的长宽高分别为15.5 m×9 m×4 m。

2 不同模型回波信号计算与分析

对雷达发射的电磁波而言，极化特征表明了电场强度的取向和幅度随着时间而变化的性质，雷达发射电磁波为完全极化电磁波。对一个沿空间直角坐标系中+z轴方向传播的单一频率电磁波而言，在水平垂直极化基下，其电场矢量[1]可以简记为

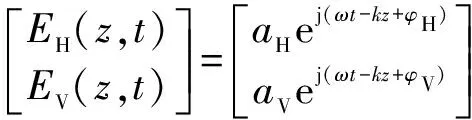
(4)

式中：ω=2πc/λ；k=2π/λ为波数，λ为电磁波波长；φH,φV为电磁波水平、垂直极化分量的相位；

aH,aV为电磁波水平、垂直极化分量的幅度。

(5)

式中：γ=arctan(aV/aH)；φ=φV-φH； (γ,φ)∈[0,π/2]×[0,2π]。

将建立好的模型导入FEKO软件，进行网格剖分，对箔条云模型而言，结合矩量法和快速多极子算法分析箔条云的单站远场回波特性以及极化特征。对救生艇和飞机模型而言，由于剖分后未知量较大，结合高频近似法进行计算。设定入射电磁波为垂直极化的平面波，电磁波频率为10 GHz，幅度为1，初相为0°，入射方向θ=90°(平视)，φ=0°～360°，其中φ的间隔角度为2°。

对4 000根在空间服从半径为1 m的球均匀分布箔条云模型，同极化和交叉极化接收时，回波信号电场强度大小如图4所示，极化比结果如图5所示。

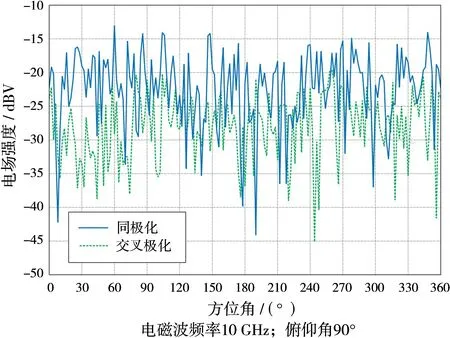
图4 不同接收极化的箔条云雷达回波信号

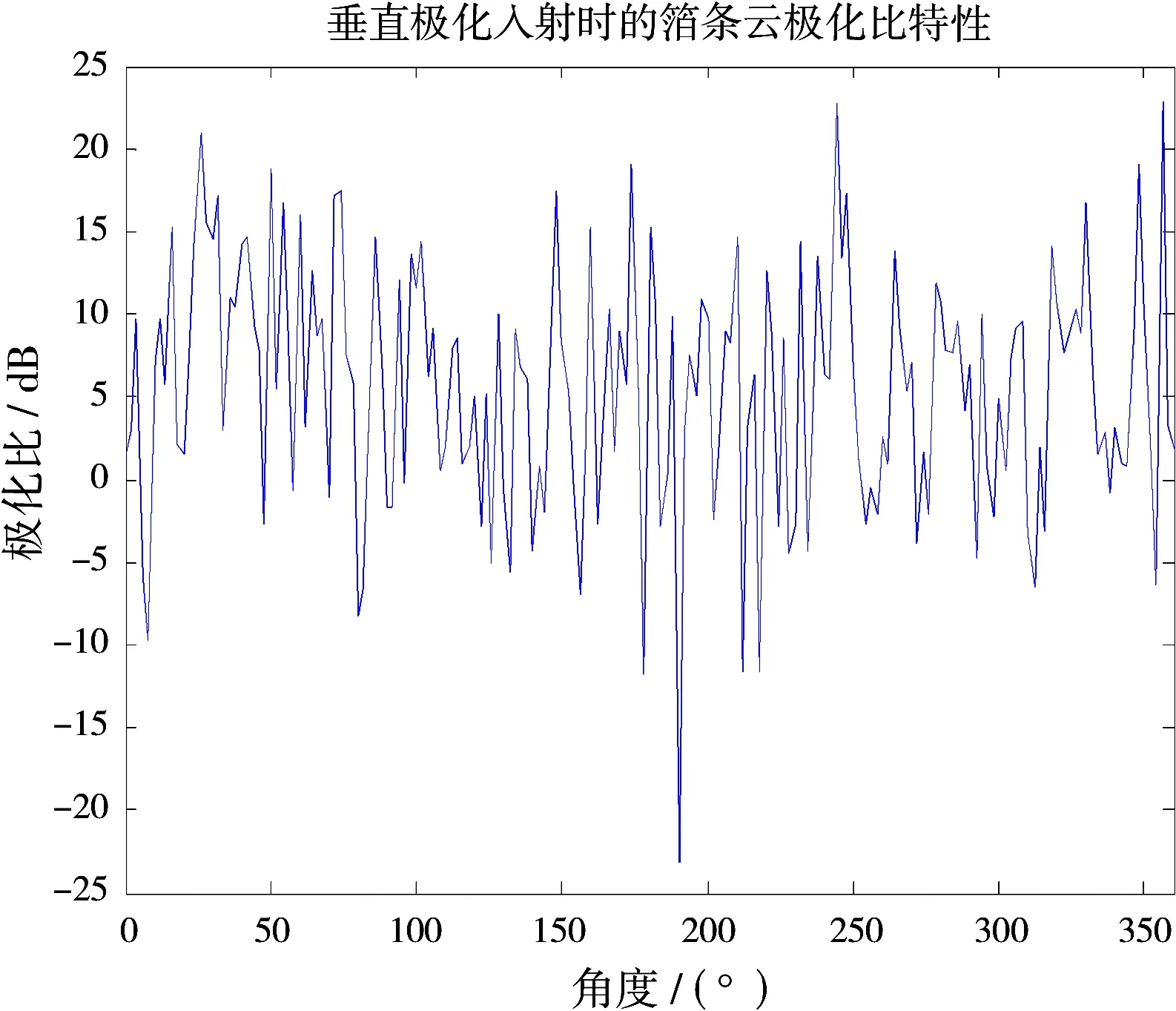
图5 箔条云极化比变化示意图

图4中横轴为电磁波的入射方向，纵轴为回波信号的电场强度。实线和虚线分别表示同极化接收和交叉极化接收时回波信号的电场强度。由图4可以看出，在该密度下的箔条云模型，不同角度的雷达回波信号起伏较大，并且同极化与交叉极化回波信号幅度之间没有明显的大小关系。

图5为不同角度极化比计算结果，横轴为电磁波入射方向，纵轴为极化比数值。由图5可以看出，箔条云极化比大多分布在-5 dB到15 dB之间，计算得到极化比平均值为5.133 1 dB。由于箔条云在空间均匀分布，且箔条空间姿态角随机取值，导致极化比分布比较随机。随着箔条云密度的增加，极化比的起伏变化有所改善。

不同接收极化的救生艇雷达回波信号幅度和极化比计算结果分别如图6、图7所示。飞机的计算结果分别如图8、图9所示。

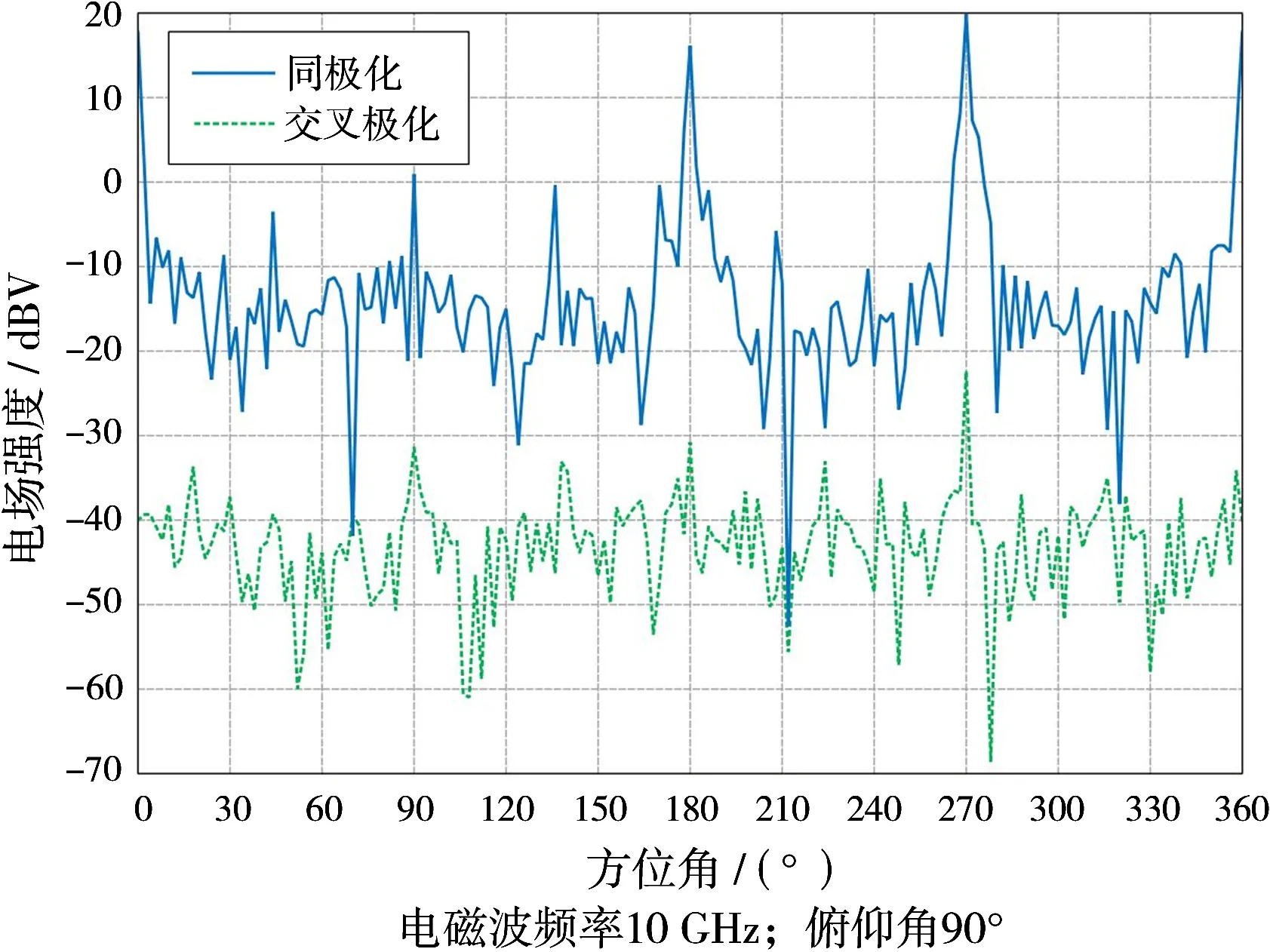
图6 救生艇不同接收极化方式计算结果

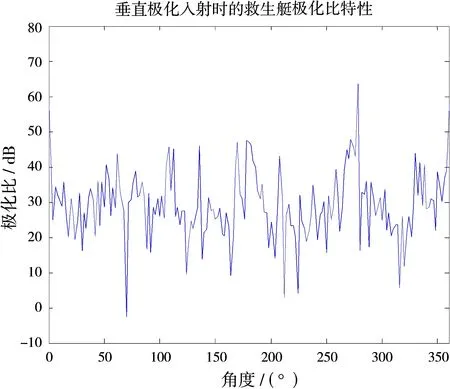
图7 救生艇极化比变化示意图

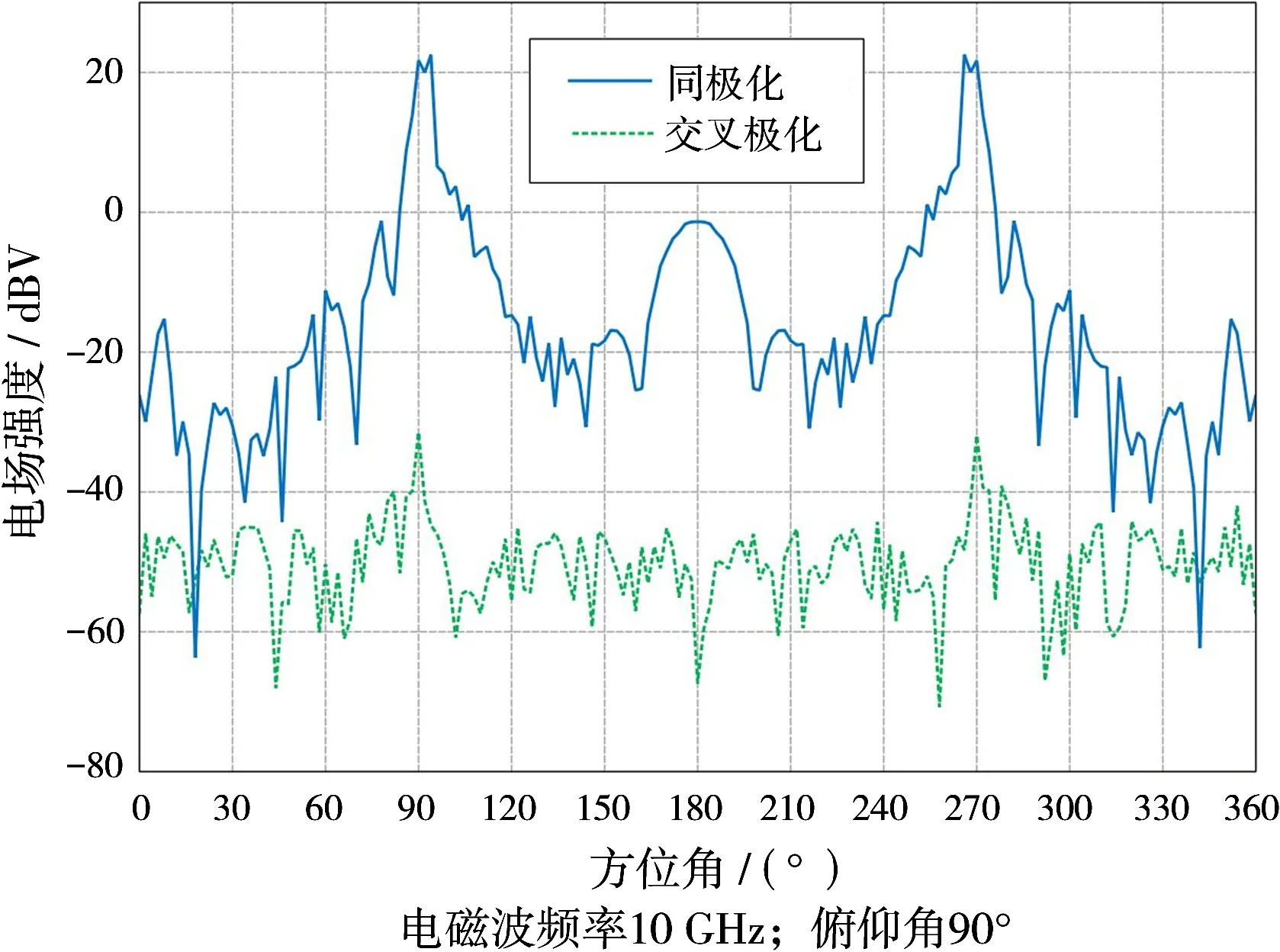
图8 飞机不同接收极化方式计算结果

图9 飞机极化比变化示意图

由图6可以看出，救生艇在不同接收极化方式下的回波幅度大小区分明显，且都呈现出同极化远大于交叉极化的特点，不同极化方式下的雷达回波信号电场强度之差普遍在20 dB以上。在入射角度为180°，270°和360°(0°)时，救生艇的雷达回波信号幅度出现峰值，此时分别对应救生艇的右侧、后侧和左侧，这是由于电磁波传播方向横截面上救生艇的截面积较大造成的。由图7可以看出，救生艇极化比计算结果大都分布在20 dB到40 dB之间，计算得到救生艇的极化比平均值为29.221 2 dB。

由图8可以看出，飞机在不同接收极化方式下的回波幅度大小也区分明显，呈现出同极化远大于交叉极化的特点。在入射角度为90°和270°时，雷达回波信号电场强度出现两个较大的峰值，此时对应飞机的左侧和右侧，180°时对应飞机的后侧。结合图8和图9可以看出，飞机的极化比变化

趋势与同极化接收幅度的变化趋势相同，且极化比最大值与回波幅度的最大值一一对应。除了飞机正前方左右各20°和40°时对应的极化比比值较小以外，其他角度的极化比结果均在10 dB以上，计算得到飞机的极化比平均值为33.839 6 dB。

由图6和图8可以看出，对船和飞机类目标而言，不同角度交叉极化接收的雷达回波信号幅度分布较为平缓，而同极化接收的回波幅度起伏剧烈，随姿态角变化敏感，目标侧向的回波幅度普遍较大，不同角度间的回波幅度差值最大可达70 dB，甚至更大。救生艇和飞机的极化比计算结果平均值均远大于箔条云，因此，通过极化比特征的差异来区分箔条干扰与其他目标是可行的。

3 结束语

为提高制导雷达区分箔条干扰和其他目标的能力，将电磁场数值计算方法引入到不同类型目标极化特征的计算，分别建立了救生艇、飞机和球均匀分布的箔条云模型，利用FEKO软件对不同目标、不同入射角度的雷达回波信号进行计算，分析不同目标之间极化特征的差别，结果表明常见目标(船和飞机)的极化比远大于箔条干扰的极化比，极化比平均值相差一个数量级。基于以上结论，制导雷达可以通过极化比特征对箔条干扰和常见目标进行识别，从而实现制导雷达目标识别能力的提高。

[1] 陈静. 雷达箔条干扰原理[M]. 北京：国防工业出版社, 2007.

[2] 章力强,李相平,陈信. 箔条假目标干扰极化识别与抑制技术[J]. 制导与引信, 2012, 33(1):19-23.

[3] 党晓江,李政杰,李欣,等. 极化捷变末制导雷达抗机载箔条质心干扰研究[J]. 系统仿真学报, 2014, 26(8):1807-1813.

[4] 李金梁,曾勇虎,申绪涧,等. 改进的箔条干扰极化识别方法[J]. 雷达科学与技术, 2015, 13(4):350-355.

LI Jinliang, ZENG Yonghu, SHEN Xujian, et al. Modified Polarization Recognition Method for Chaff Jamming[J]. Radar Science and Technology, 2015, 13(4):350-355.(in Chinese)

[5] TANG B, LI H M, SHENG X Q. Jamming Recognition Method Based on the Full Polarisation Scattering Matrix of Chaff Clouds[J]. IET Microwaves, Antennas & Propagation, 2012, 6(13):1451-1460.

[6] 蔡万勇,李侠,万山虎,等. 大气环境下箔条运动轨迹及箔条幕扩散模型[J]. 系统工程与电子技术, 2009, 31(3):565-569.

[7] 华翔,高武奇. 箔条干扰弹可视化建模及仿真[J]. 西安工业大学学报, 2010, 30(4):392-395.

[8] 董继进,刘忠,毛超. 基于高速旋转飞行器的箔条抛撒运动特性[J]. 海军工程大学学报, 2013, 25(5):83-87.

[9] 李春舢,韩丽,张革之,等. 某箔条干扰弹的优化设计[J]. 科技致富向导, 2015(14):221.

[10] 李亚飞,潘莉莉. 基于散射特性的混装箔条云RCS计算与仿真[J]. 舰船电子工程, 2015, 35(1):84-86.

[11] 李金梁. 箔条干扰的特性与雷达抗箔条技术研究[D]. 长沙：国防科技大学, 2010.